Матрицаға амалдар қолдану. 1.9. Матрицаға амалдар қолдану. 1. Матрицаа амалдар олдану Матрицаны сана кбейту
 Скачать 81.33 Kb. Скачать 81.33 Kb.
|
|
1. 9. Матрицаға амалдар қолдану Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек: Мысалы, 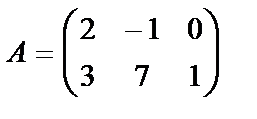 матрицасын матрицасын Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес. 2. Матрицаларды қосу және алу. Өлшемдері бірдей матрицаларды ғана қосуға болады. А және В матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз: А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті:A – B = A+(-1)B немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады. Мысалы А матрицасынан В матрицасын алайық: 3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі mxk болатын А матрицасы мен өлшемі kxn болатын В матриасы берілсін: Осы екі матрицаны көбейткенде өлшемі mxn болатын көбейтінді С матрица аламыз: С матрицасының сij элементі А матрицаның i–жатық жол элементтерін В матрицаның j –тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады: 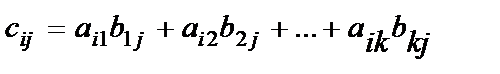 . (1) . (1) Мысалы, 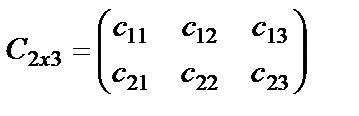 . k=3 болғандықтан (1) формуланы қолданғанда үш қосылғыш болады: . k=3 болғандықтан (1) формуланы қолданғанда үш қосылғыш болады: C= 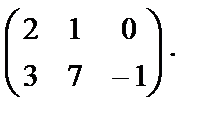  = = Қосу және көбейту амалдарының мынадай қасиеттері бар:
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық. 8) Біріншіден, екі матрицаның АВ көбейтіндісі болғанмен ВА көбейтіндісі болмауы мүмкін. Мысалы, A2*3*B3*3 көбейтіндісі бар, бірақ B3*3 *A2*3 көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес; екіншіден, АВ және ВА көбейтінділері бар болғанмен, олардың өлшемдері әртүрлі болуы мүмкін. Мысалы, A2*3*B3*2 және B3*2 *A2*3 көбейтінділер бар, бірақ өлшемдері әртүрлі: A2*3*B3*2=C2*2, B3*2 *A2*3=C3*3; үшіншіден, АВ және ВА көбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ ≠BA. Мысал. 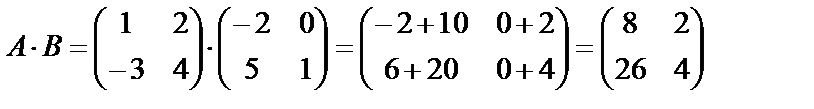 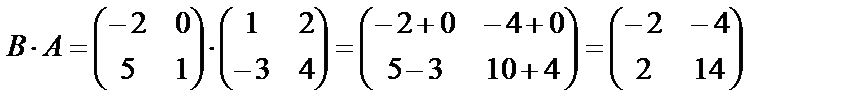 Көріп отырғанымыздай АВ ≠BA. 9) А-квадрат матрица болса, онда мына теңдік орындалады: АЕ = ЕА = А. |
