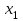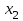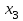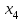тест студенттерге (копия). Таырып матрицалар
 Скачать 84.41 Kb. Скачать 84.41 Kb.
|
|
Тақырып: МАТРИЦАЛАР.АНЫҚТАУЫШТАР. СТЖ Деңгей: БІЛУ #1 *!Матрицаның анықтауышы -бұл #2 Матрица – бұл #3 *!Анықтауыш миноры -бұл: #4 *!Диагональ матрица деп аталады: #5 *!Матрицаға сан көбейту үшін: #6 *!Матрицаны бірлік матрицаға көбейту кезінде алынады: #7 *!Анықтауыштың екі параллель жолын ауыстырған кезде анықтауыш қалай өзгереді? #8 *! Анықтауыштың өлшемі : #9 *!Үшбұрыш ережесі: #10 *!Сызықтық теңдеулер жүйесі үйлесімді, егер келесі шарт орындалса: #11 *!Сызықтық теңдеулер жүйесі біртекті, егер #12 *!Егер теңдеулер жүйесі берілген жүйеге тең болса, онда #13 *!Егер сызықтық теңдеулер жүйесінде шешім болмаса, онда жүйе ... аталады: #14 *! Гаусс әдісімен теңдеулер жүйесін шешу барысында мүмкін емес #15 *!Сызықтық теңдеу жүйелерін шешудің матрицалық әдісі тек ... матрицалар үшін қолданылады: #16 *!Гаусс әдісі бойынша тура жүріс нәтижесінде сызықтық теңдеулер жүйесін шешу: #17 *! А*A-1матрицалараның көбейтіндісі, мұндағы А-1 – кері матрица, тең: #18 *!n-белгісіздердің саны, m-жүйенің теңдеулерінің саны. Крамер ережесін қолдануды қамтамасыз ететін шарт #19 *!Кері матрицаны есептеу әдісі: #20 *!Кері матрица бар, егер... болса Деңгей: ТҮСІНУ #1 *! B матрицасы берілген. 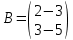 BТ көрсетіңіз BТ көрсетіңіз#2 *! матрицасы берілген. 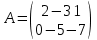 АТ табыңыз АТ табыңыз#3 *! Матрицаның анықтауыш А = 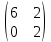 #4 *! А = 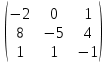 матрицаның а21 элементін көрсетіңіз матрицаның а21 элементін көрсетіңіз#5 *! Егер 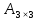 = = 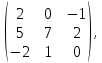 ал ал 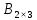 = = 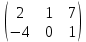 болса, онда С = А болса, онда С = А ВТ матрицасының өлшемі ВТ матрицасының өлшемі #6 *! А = 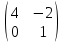 берілген. -2A матрицасы берілген. -2A матрицасы#7 *! А = 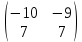 және В = және В = 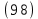 матрицалардың а22 және b 12 элементтерін көрсетіңіз матрицалардың а22 және b 12 элементтерін көрсетіңіз #8 *! А = 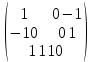 берілген. A+B амалы орындалу үшін В матрицасының өлшемін көрсетіңіз берілген. A+B амалы орындалу үшін В матрицасының өлшемін көрсетіңіз #9 *! А = 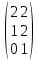 берілген. A*B амалы орындалу үшін В матрицасының өлшемін көрсетіңіз берілген. A*B амалы орындалу үшін В матрицасының өлшемін көрсетіңіз #10 *! A*B амалы орындалатын матрицаны көрсетіңіз #11 *! А = 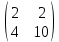 , В = , В = 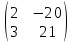 және С = және С = 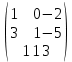 матрицалары берілген. Көбейту амалы орындалатын матрицаларды көрсетіңіз матрицалары берілген. Көбейту амалы орындалатын матрицаларды көрсетіңіз#12 *!А = 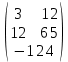 , В = , В = 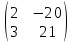 және С = және С = 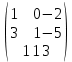 матрицалары берілген. Азайту амалы орындалатын матрицаларды көрсетіңіз матрицалары берілген. Азайту амалы орындалатын матрицаларды көрсетіңіз#13 *! 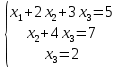 жүйесінің бас анықтауышы: жүйесінің бас анықтауышы:#14 *!  жүйесінің жүйесінің 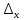 қосымша анықтауышы: қосымша анықтауышы:#15 *! 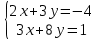 жүйесінің жүйесінің 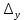 қосымша анықтауышы: қосымша анықтауышы:#16 *! 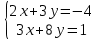 жүйесінің бас анықтауышы: жүйесінің бас анықтауышы:#17 *! 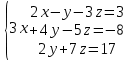 жүйесінің бас анықтауышы: жүйесінің бас анықтауышы:#18 *!Егер жүйенің анықтауышы нөлге тең болса, ал белгісіздердің анықтауыштары нөлге тең болмаса, онда #19 *! Егер А(2×3), В(3×2) болса, онда С=АВ неге тең #20 *! А-1 матрицасы А матрицасына кері матрица деп аталады, егер ТАҚЫРЫП: ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР Деңгей:БІЛУ #1 *!Екінші ретті дифференциалдық теңдеудің жалпы шешімі: #2 *! Бірінші ретті дифференциалдық теңдеудің жалпы шешімі: #3 *! Дифференциалдық теңдеудің реті #4 *!Айнымалылары ажыратылған дифференциалдық теңдеу #5 *! Айнымалылары ажыратылатын дифференциалдық теңдеу: #6 *!n-ші ретті дифференциалдық теңдеу: #7 *!Егер f(x)=0 болса, онда 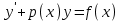 теңдеуі: теңдеуі:#8 *!Дифференциалдық теңдеу деп.....байланыстыратын қатынасты айтады #9 *!Ізделінді функция бір айнымалыдан тәуелді болса, онда дифференциалдық теңдеу.....деп аталады: #10 *!Жалпы шешімнен 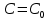 мәніне тең болғанда алынған мәніне тең болғанда алынған 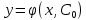 функциясы функциясы #11 *!Коши есебі дегеніміз... #12 *!Айнымалылары ажыратылған дифференциалдық теңдеу #13 *! n-ші ретті дифференциалдық теңдеудің жалпы түрі: #14 *!Дифференциалдық теңдеудің орнына қойғанда оны теңбе-теңдікке айналдыратын кез-келген функция... #15 *!Сызықтық біртекті емес дифференциалдық теңдеуді шешудің ... әдісі Уровень: ПОНИМАНИЕ #1 *!2-ші ретті дифференциалдық теңдеу #2 *! Сызықтық біртекті дифференциалдық теңдеу #3 *! Сызықтық біртекті емес дифференциалдық теңдеу #4 *! Бірінші ретті дифференциалдық теңдеу #5 *! 3-ші ретті дифференциалдық теңдеу #6 *! Айнымалылары ажыратылатын дифференциалдық теңдеу #7 *! 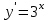 дифференциалдық теңдеуінің жалпы шешімі: дифференциалдық теңдеуінің жалпы шешімі:#8 *! Сызықтық біртекті емес дифференциалдық теңдеу #9 *! Айнымалылары ажыратылатын дифференциалдық теңдеу #10 *! Сызықтық біртекті емес дифференциалдық теңдеу #11 *! #12 *! 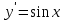 дифференциалдық теңдеуінің жалпы шешімі:: дифференциалдық теңдеуінің жалпы шешімі::#13 *! 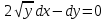 дифференциалдық теңдеуді шешу әдісі дифференциалдық теңдеуді шешу әдісі #14 *!Төмендегі есептердің ішінде «Коши есебі»: #15 *! 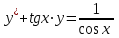 сызықтық дифференциалдық теңдеуінің p(x) және g(x) функциялары сызықтық дифференциалдық теңдеуінің p(x) және g(x) функцияларыТЕМА: ПРЕДЕЛЫ, ПРОИЗВОДНАЯ и ДИФФЕРЕНЦИАЛ Уровень: ЗНАНИЯ #1 *!Егер белгілі бір нүктедегі функцияның шегі мен функцияның мәні тең болса, онда осы нүктеде функцияның аталуы #2 *! Егер функция интервалдың әр нүктесінде үзіліссіз болса, онда оны #3 *!Екі функцияның туындыларының қосындылары тең #4 *! Формулалардың қайсысы тамаша шекке жатпайды? #5 *! Формулалардың қайсысы тамаша шекке жатады ? #6 *! Мына формула 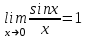 қалай аталады? қалай аталады? #7 *! Тұрақты С шаманың шегі: #8 *! Егер 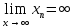 , , онда , , онда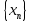 тізбегі ... деп аталады тізбегі ... деп аталады#9 *! Шектің нүктедегi қасиетi: #10 *!Егер 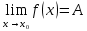 және және 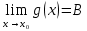 болса, онда болса, онда 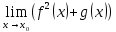 функциясының шегі неге тең функциясының шегі неге тең#11 *! Функцияның туындысын табудың аталуы #12 *! Экспонентаның туындысын табу формуласын көрсетіңіз #13 *! С тұрақты санның туындысы тең #14 *! Бірінші ретті туындының физикалық мағынасының қандай? #15 *! y=f(x) функциясының дифференциалы #16 *! Екі дифференциалданатын функцияның көбейтіндісінің туындысы тең #17 *!du+dv өрнегі қандай функцияның дифференциалына сәйкес келеді? #18 *! Егер 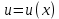 тең болғандағы, тең болғандағы, 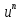 күрделі функцияның туындысы күрделі функцияның туындысы#19 *!у =cf(x) функциясының туындысы (с-берілген сан) тең #20 *! 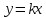 функциясының дифференциалы функциясының дифференциалыУровень: ПОНИМАНИЕ #1 *! Функция үзліссіз емес нүктелердің аталуы: #2 *!Келесі шектердің қайсы нөлге тең #3 *! 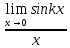 шегінің мәні шегінің мәні#4 *! Егер функция 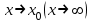 ұмтылғанда ұмтылғанда 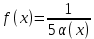 функциясының мәні функциясының мәні #5 *! Егер функция 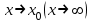 ұмтылғанда ұмтылғанда 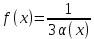 функциясының мәні функциясының мәні #6 *! 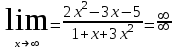 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі #7 *! 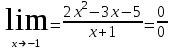 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі #8 *! 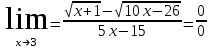 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі #9 *! 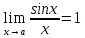 теңдігі дұрыс болатындай а мәнін табыңдар теңдігі дұрыс болатындай а мәнін табыңдар#10 *! y 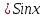 функциясының дифференциалы функциясының дифференциалы#11 *!Дұрыс мәлімдемені таңдаңыз #12 *! 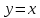 функциясының дифференциалы функциясының дифференциалы#13 *! 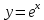 функциясының дифференциалы функциясының дифференциалы#14 *!(kx+b)’= #15 *!Функцияның дифференциалы: 16 *!Берілген нүктеде туындысы бар функция ... деп аталады #17 *! 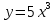 функциясының туындысы функциясының туындысы#18 *!Функция өсімшесінің негізгі бөлігі #19 *! 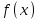 функциясының х нүктесіндегі туындысының анықтамасы функциясының х нүктесіндегі туындысының анықтамасы#20 *! 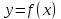 функциясы өсімшесінің функциясы өсімшесінің 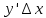 бас бөлігі ... деп аталады бас бөлігі ... деп аталадыТЕМА: ПРЕДЕЛЫ, ПРОИЗВОДНАЯ и ДИФФЕРЕНЦИАЛ Уровень: ЗНАНИЯ #1 *!Егер белгілі бір нүктедегі функцияның шегі мен функцияның мәні тең болса, онда осы нүктеде функцияның аталуы #2 *! Егер функция интервалдың әр нүктесінде үзіліссіз болса, онда оны #3 *!Екі функцияның туындыларының қосындылары тең #4 *! Формулалардың қайсысы тамаша шекке жатпайды? #5 *! Формулалардың қайсысы тамаша шекке жатады ? #6 *! Мына формула 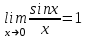 қалай аталады? қалай аталады? #7 *! Тұрақты С шаманың шегі: #8 *! Егер 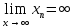 , , онда , , онда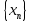 тізбегі ... деп аталады тізбегі ... деп аталады#9 *! Шектің нүктедегi қасиетi: #10 *!Егер 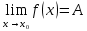 және және 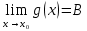 болса, онда болса, онда 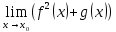 функциясының шегі неге тең функциясының шегі неге тең#11 *! Функцияның туындысын табудың аталуы #12 *! Экспонентаның туындысын табу формуласын көрсетіңіз #13 *! С тұрақты санның туындысы тең #14 *! Бірінші ретті туындының физикалық мағынасының қандай? #15 *! y=f(x) функциясының дифференциалы #16 *! Екі дифференциалданатын функцияның көбейтіндісінің туындысы тең #17 *!du+dv өрнегі қандай функцияның дифференциалына сәйкес келеді? #18 *! Егер 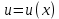 тең болғандағы, тең болғандағы, 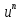 күрделі функцияның туындысы күрделі функцияның туындысы#19 *!у =cf(x) функциясының туындысы (с-берілген сан) тең #20 *! 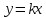 функциясының дифференциалы функциясының дифференциалыУровень: ПОНИМАНИЕ #1 *! Функция үзліссіз емес нүктелердің аталуы: #2 *!Келесі шектердің қайсы нөлге тең #3 *! 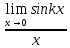 шегінің мәні шегінің мәні#4 *! Егер функция 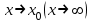 ұмтылғанда ұмтылғанда 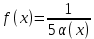 функциясының мәні функциясының мәні #5 *! Егер функция 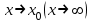 ұмтылғанда ұмтылғанда 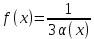 функциясының мәні функциясының мәні #6 *! 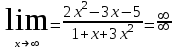 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі #7 *! 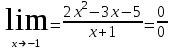 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі #8 *! 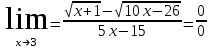 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі #9 *! 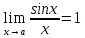 теңдігі дұрыс болатындай а мәнін табыңдар теңдігі дұрыс болатындай а мәнін табыңдар#10 *! y 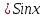 функциясының дифференциалы функциясының дифференциалы#11 *!Дұрыс мәлімдемені таңдаңыз #12 *! 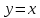 функциясының дифференциалы функциясының дифференциалы#13 *! 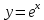 функциясының дифференциалы функциясының дифференциалы#14 *!(kx+b)’= #15 *!Функцияның дифференциалы: 16 *!Берілген нүктеде туындысы бар функция ... деп аталады #17 *! 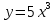 функциясының туындысы функциясының туындысы#18 *!Функция өсімшесінің негізгі бөлігі #19 *! 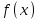 функциясының х нүктесіндегі туындысының анықтамасы функциясының х нүктесіндегі туындысының анықтамасы#20 *! 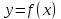 функциясы өсімшесінің функциясы өсімшесінің 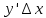 бас бөлігі ... деп аталады бас бөлігі ... деп аталадыТЕМА: ТЕОРИЯ ВЕРОЯТНОСТЕЙ. СЛУЧАЙНЫЕ СОБЫТИЯ Уровень: ЗНАНИЯ #1 *! PA(В) шартты ықтималдық – бұл: #2 *!Егер бүкіл кеңістікті құрайтын n үйлесімсіз Hi оқиғаларынан тұратын топ бар болып, P(Hi) ықтималдықтары белгілі болса, ал А оқиғасы Hi-нің біреуі орын алғаннан кейін пайда болуы мүмкін және PA(Hi) ықтималдығы белгілі болса, онда P есептелетін формула: #3 *!Екі оқиғаның көбейтіндісі деп … жаңа оқиға аталады : #4 *!Болжам деп аталатын оқиғалар: #5 *! Оқиға- бұл: #6 *!Оқиғалардың толық жиынын құрайды: #7 *! А және В оқиғаларының қосындысы деп... аталады. #8 *! Тәуелсiз оқиғалардың бiрге пайда болу ықтималдығы: #9 *!Тәуелдi оқиғалардың бiрге пайда болу ықтималдығы: #10 *!Сынау нәтижесiнде мiндеттi түрде пайда болатын оқиға #11 *! А оқиғасы толық топ құрайтын үйлесiмсiз В1, В2,…, Вn оқиғаларының бiрi орындалғанда ғана пайда болады. Бұл оқиғалардың қайсысы орындалатыны алдын ала белгiсiз болғандықтан, олар: #12 *! Р(А+В) символы ненi бiлдiредi? #13 *!Толық ықтималдық формуласы #14 *!Бернулли формуласы: #15 *!Лапластың интегралдық формуласы қандай ықтималдықтарды есептейдi: Уровень: ПОНИМАНИЕ #1 *!Нысанаға үш рет оқ атылды. Ai оқиғасы - i-ші рет атқандағы нысанаға тию болсын. Олай болса, 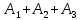 оқиғасының мағынасы: оқиғасының мағынасы:#2 *!Нысанаға үш рет оқ атылды. Ai оқиғасы - i-ші рет атқандағы нысанаға тию болсын. Олай болса, 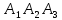 оқиғасының мағынасы: оқиғасының мағынасы:#3 *!Нысанаға үш рет оқ атылды. Ai оқиғасы - i-ші рет атқандағы нысанаға тию болсын. Олай болса 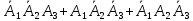 оқиғасының мағынасы: оқиғасының мағынасы:#4 *!Нысанаға үш рет оқ атылды. Ai оқиғасы - i-ші рет атқандағы нысанаға тию болсын. Олай болса 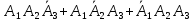 оқиғасының мағынасы: оқиғасының мағынасы:#5 *!Тұтынушы қандай да бір тауардың жарнамасын теледидардан (А оқиғасы), жарнамалық стендтен (В оқиғасы) көруі және газеттен оқуы (С оқиғасы) мүмкін. 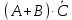 оқиғасының мағынасы: оқиғасының мағынасы:#6 *!Егер А оқиғасы – қыз кездесуге келген жоқ, В оқиғасы – жігіт кездесуге келген жоқ болса, онда С=A+B оқиғасының мағынасы: #7 *! Егер әр сынақта А оқиғасының пайда болу ықтималдығы 0,002 болса, онда А оқиғасының 1000 сынақта 3 рет пайда болу ықтималдығын табу үшін қай формула қолданылады: #8 *!Егер әр сынақта а оқиғасының басталу ықтималдығы 0,25 болса, онда А оқиғасының 1000 сынақта 215-тен 300 есеге дейін болу ықтималдығын табу үшін мына формула бойынша есептеледі: #9 *!А және В оқиғалары үйлесімсіз деп аталады, егер: #10 *!Н1, Н2, …, Hk болжамдарының тек бірімен ғана бірге орындала алатын А оқиғасының толық ықтималдығын есептейтін формулада ол болжамдар ықтималдықтарының қосындысы 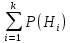 тең тең#11 *!Детальдардың екі жинағы бар. Бірінші жинақтың деталі стандартты болу ықтималдығы р1, ал екіншінің – р2. Кездейсоқ алынған детальдың стандартты болу ықтималдығы: #12 *!А1 оқиғасы – студент бірінші емтиханды тапсырады, А2 оқиғасы – студент екінші емтиханды тапсырады, А3 – студент үшінші емтиханды тапсырады. Студент тек бір ғана емтиханды тапсыру ықтималдығн есептеу формуласы #13 *! А1, А2,…,Аn оқиғаларының кемiнде бiреуiнiң пайда болу ықтималдығы: #14 *!Пуассон формуласы ... ықтималдығын есептейдi: #15 *!"Студент" сөзiнен сәтiне қарай бiр әрiп таңдалды. Таңдалынған әрiптiң дауысты болу ықтималдығы қандай? ТЕМА: ТЕОРИЯ ВЕРОЯТНОСТЕЙ. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Уровень: ЗНАНИЯ #1 *!Х дискретті кездейсоқ шаманың математикалық күтімі төмендегі формула бойынша есептеледі #2 *!Үздiксiз кездейсоқ шаманың ықтималдықтарының таралу тығыздығы: #3 *! Х дискретті кездейсоқ шаманың дисперсиясы төмендегі формула бойынша есептеледі #4 *! Тұрақты көбейткіш дисперсияның алдына D(CX)= #5 *! Кездейсоқ шамалардың дисперсияларының қосындысы(айырымы) тең: #6 *! Тұрақты шаманың дисперсиясы тең …: #7 *!Кездейсоқ шама мен оның математикалық күтімінің айырымы #8 *! Кездейсоқ шаманың қандай негізгі түрлерін зерттеуші кездестіреді? #9 *!Белгiлi ықтималдықтары бар жеке, дербес мәндерді қабылдайтын шама #10 *!*!Қандай да бiр ақырлы немесе ақырсыз аралықтағы барлық мәндерді қабылдайтын шама Уровень: ПОНИМАНИЕ #1 *!Дискретті кездейсоқ шаманың таралу функциясы... функция: #2 *! Үзіліссіз кездейсоқ шаманың таралу функциясы... функция: #3 *! Үздіксіз кездейсоқ шамасының берілген аралыққа түсу ықтималдығы мынадай формула бойынша есептеледі: #4 *! Пуассонның таралу заңы деп, ықтималдығы... формуласымен анықталатын таралуды айтамыз #5 *!Х және У тәуелсіз кездейсоқ шамалардың математикалық күтімдері сәйкесінше М(Х)=2, М(Y)=4 тең. Егер Z кездейсоқ шамасы Z=2X-Y+3 тең болса, М(Z) табыңыз: #6 *! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. Р1 ықтималдығын табыңыз?
#7 *!Х кездейсоқ шамасын kтұрақты көбейткішке көбейткенде, оның математикалық күтімі қалай өзгереді: #8 *!Х кездейсоқ шамаға а саны қосылды. Осыдан оның дисперсиясы қалай өзгереді? #9 *! 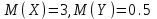 берілген. берілген. 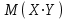 табыңыз. табыңыз.#10 *!Д 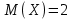 берілген. М(2Х)= табыңыз. берілген. М(2Х)= табыңыз.ТЕМА: ИНТЕГРАЛЫ Уровень: ЗНАНИЯ #1 *!Х аралығында y=F(x) функциясы y=f(x) функциясы үшін алғашқы функция деп аталады, егер x #2 *! Х аралығында 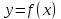 функциясы үшін, функциясы үшін, 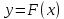 функциясы қалай аталады егер функциясы қалай аталады егер 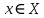 үшін осы теңдік орындалса үшін осы теңдік орындалса 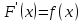 : :#3 *! 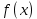 функциясы үшін алғашқы функциялардың жиыны: функциясы үшін алғашқы функциялардың жиыны:#4 *! Анықталмаған интегралды табу операциясы: #5 *!Тікелей интегралдау, алмастыру әдісі, бөліктеп интегралдау бұл: #6 *!Анықталмаған интегралдың туындысы: #7 *!Екі немесе бірнеше функцияның алгебралық қосындысының анықталмаған интегралы: #8 *!Анықталған интеграл ... формула бойынша есептеледі: #9 *!Бірдей шектері бар анықталған интеграл тең: #10 *!Интегралдың жоғарғы және төменгі шектерінің орындарын ауыстырған кезде анықталмаған интеграл: #11 *!Анықталған интеграл ... табуға қолданылады: #12 *! 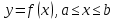 функциясы мен берілген қисықтың доғасының ұзындығының формуласы: функциясы мен берілген қисықтың доғасының ұзындығының формуласы:#13 *! Төменнен 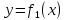 , жоғарыдан , жоғарыдан 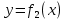 функцияларының графигімен шектелген, және x=a, x=b, a функцияларының графигімен шектелген, және x=a, x=b, a#14 *!Бөліктеп интегралдау формуласы: #15 *! n-нiң қандай мәнiнде 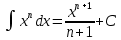 орындалмайды: орындалмайды:#16 *! Анықталмаған интегралдың дифференциалы: #17 *! Егер С – тұрақты сан болса, онда 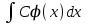 #18 *!Анықталған интеграл ... формула бойынша есептеледі: #19 *!Анықталған интегралдың бөліктеп интегралдау формуласы #20 *! Төменнен 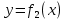 , жоғарыдан , жоғарыдан 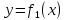 функцияларының графигімен шектелген, ауданының формуласы функцияларының графигімен шектелген, ауданының формуласыУровень: ПОНИМАНИЕ #1 *! Анықталмаған интегралдарды бөліктеп интегралдау әдісі қай кезде қолданылады: #2 *!Интегралдың айнымалыны ауыстыру әдісі (алмастыру әдісі) не үшін қолданылады: #3 *!Функцияның бірнеше алғашқы функциясы бола ма: #4 *! Берілген интегралдардың ішінде бөліктеп интегралдау бойынша алынады: #5 *! Берілген интегралдардың ішінде тікелей интегралдау бойынша алынады: #6 *!1 санының анықталмаған интегралы тең: *1 #7 *! Берілген интегралдардың ішінде тікелей интегралдау бойынша алынады: #8 *! 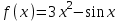 функциясының алғашқы функциясы: функциясының алғашқы функциясы:#9 *! Барлық алғашқы функциялардың жазылуы 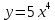 : :#10 *! Анықталған интегралдың дұрыс емес қасиеттері: #11. *! Анықталған интегралдың дұрыс емес қасиеттері: #12 *! Анықталған интегралдың қасиеті бойынша 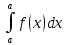 тең: тең:#13 *! Берілген интегралдардың ішінде бөліктеп интегралдау бойынша алынады: #14 *! Анықталған интеграл 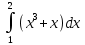 мына формула бойынша есептеледі: мына формула бойынша есептеледі:#15 *! 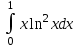 интегралын есептеу әдісі: интегралын есептеу әдісі: #16 *! 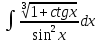 интегралын есептеу әдісі: интегралын есептеу әдісі: #17 *! 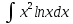 интегралындағы u мен dv дұрыс таңдаңыз: интегралындағы u мен dv дұрыс таңдаңыз: #18 *! 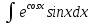 интегралын есептеу үшін қолданылатын алмастыру: интегралын есептеу үшін қолданылатын алмастыру:#19 *! 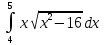 интегралын есептеу әдісі: интегралын есептеу әдісі: #20 *! Егер 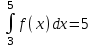 және және 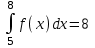 , онда , онда 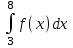 |