Контрольная работа 5 Производная и дифференциал тема производная и дифференциал Производная. Дифференциал. Производные и дифференциалы высших порядков

• Название: Контрольная работа 5 Производная и дифференциал тема производная и дифференциал Производная. Дифференциал. Производные и дифференциалы высших порядков
• Дата: 27.12.2020
• Размер: 1.42 Mb.
• Имя файла: Tema5.doc
• Тип: Контрольная работа; #164713
• страница: 1 из 5

Контрольная работа №5

Производная и дифференциал

ТЕМА 5. Производная и дифференциал
1. Производная.

2. Дифференциал.

3. Производные и дифференциалы высших порядков.

4. Свойства дифференцируемых функций.
СПИСОК ЛИТЕРАТУРЫ

1. 
   Бугров Я.С., Никольский СМ. Высшая математика: Учеб.для вузов:в Зт.-5-е изд.,стер.-М.:Дрофа .- (Высшее образование. Современный учебник).т.2. Дифференциальное и интегральное исчисление.-2003.-509 с.
   
2. 
   Пискунов Н.С Дифференциальное и интегральное исчисление: Учеб. пособие: в 2-х т.- Изд. стер. -М.: Интеграл - Пресс. Т.1. -2001.- 415 с.
   
3. 
   Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Учеб. для вузов: в 3-х томах. - 8-е изд.-М.: Физматлит. т. 1 - 2001. -697 с.
   
4. 
   Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. -22-е изд., перераб.- СПб: Профессия, 2003.-432 с.
   
5. 
   Кудрявцев Л.Д. Курс математического анализа. Учеб. для вузов: В 3-х томах. - 5-е изд., перераб. и доп. -М.: Дрофа. Т.1. - 2003.-703 с.
   
6. 
   Ильин В.А., Позняк Э.Г. Основы математического анализа. Учеб. для вузов в 2-х частях. - 6-е изд. стер. -М. Физматлит, 2002, -646 с.
   
7. 
   Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я.-6-е изд..-М.: ОНИКС 21 век, ч.2. -2002.-416 с.
   

Решение типового варианта
Пример 1.

Найти производные заданных функций
а) ;

Решение:

;

.
б) ;

Решение:

Используем формулу .

.
в) ;

Решение:

Используем формулу .

.
г) ;

Решение:

Используем формулу .

, где ;

.
д) ;

Решение:

Используем формулу .

, где ;

.
е) ;

Решение:


Пример 2.

Найти :
а) .

Решение:

Функция в примере задана неявно. Чтобы найти ее производную продифференцируем обе части равенства по x, полагая, что у есть функция от х и обозначая производную у через :

.

Выразим из полученного равенства :

;

.
б) .

Решение:

Аналогично предыдущему примеру:

;

;

.
в)

Решение:

Используем формулу .

.
Пример 3.

Найти :
а) ;

Решение:

;



б) .

Решение:




Пример 4.

Найти дифференциал функции , если .
Решение:

Воспользуемся свойством логарифма частного для упрощения формулы:

.

Используем формулу .

;


Пример 5.

Составить уравнения касательной и нормали к кривой в точке с абсциссой .
Решение:

Найдем ординату точки касания:

.

Угловой коэффициент касательной равен значению производной в точке :

.

Подставляем значения и в уравнение касательной :

,

получили уравнение касательной .

Подставляем значения и в уравнение нормали :

,

получили уравнение нормали .

Контрольная работа №5.

Вариант 1
1. Найти производные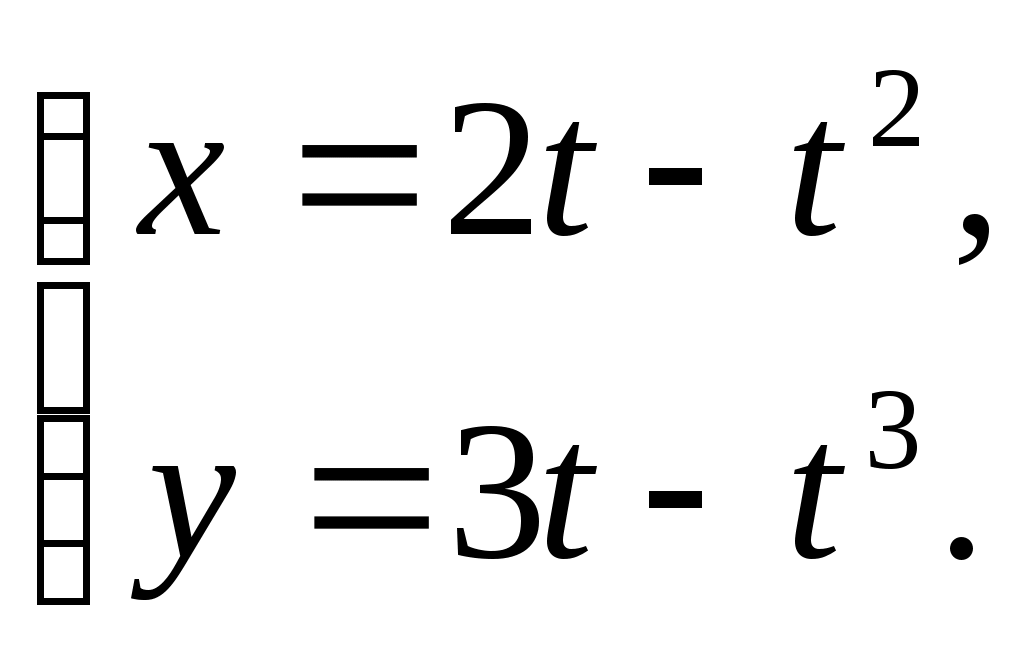

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   
7. 
   ,
   
8. 
   ,
   
9. 
   ,
   
10. 
    ,
    
11. 
    ,
    
12. 
    .
    

2. Найти :

1. 
   ,
   
2. 
   ,
   
3. 
   
   

3. Найти :



4. Найти дифференциал функции:



5. Составить уравнения касательной и нормали к линии в точке с абсциссой .
Контрольная работа №5.

Вариант 2

1. Найти производные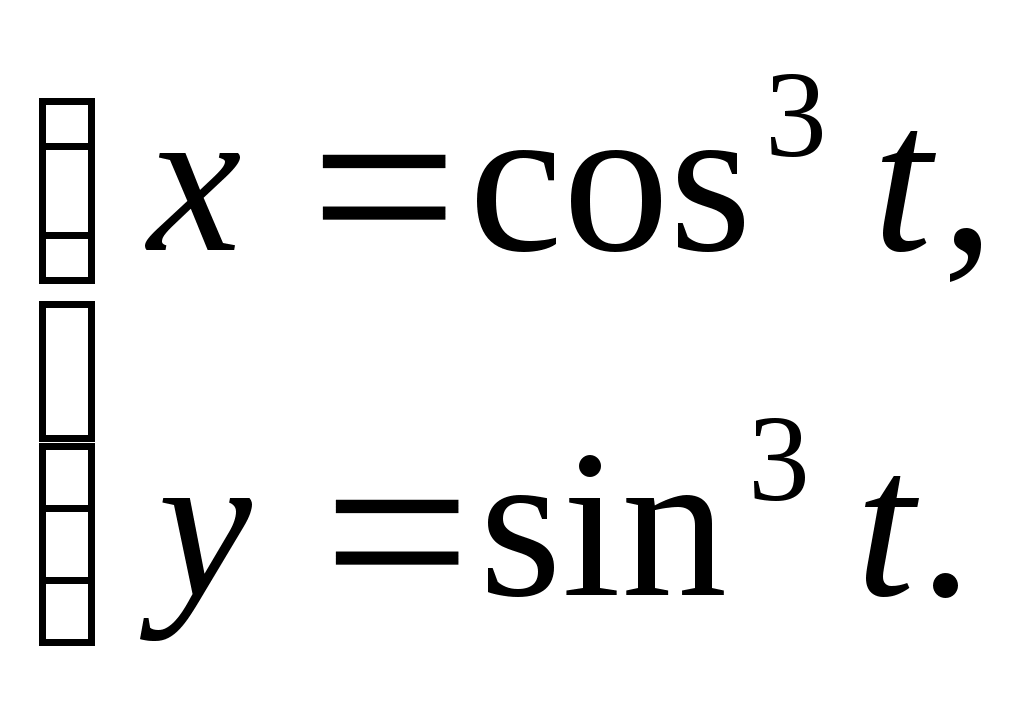

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   
7. 
   ,
   
8. 
   ,
   
9. 
   ,
   
10. 
    ,
    
11. 
    ,
    
12. 
    ,
    

2. Найти :

1. 
   ,
   
2. 
   ,
   
3. 
   
   

3. Найти :



4. Найти дифференциал функции:



5. Составить уравнения касательной и нормали к линии в точке с абсциссой .
Контрольная работа №5.

Вариант 3

1. Найти производные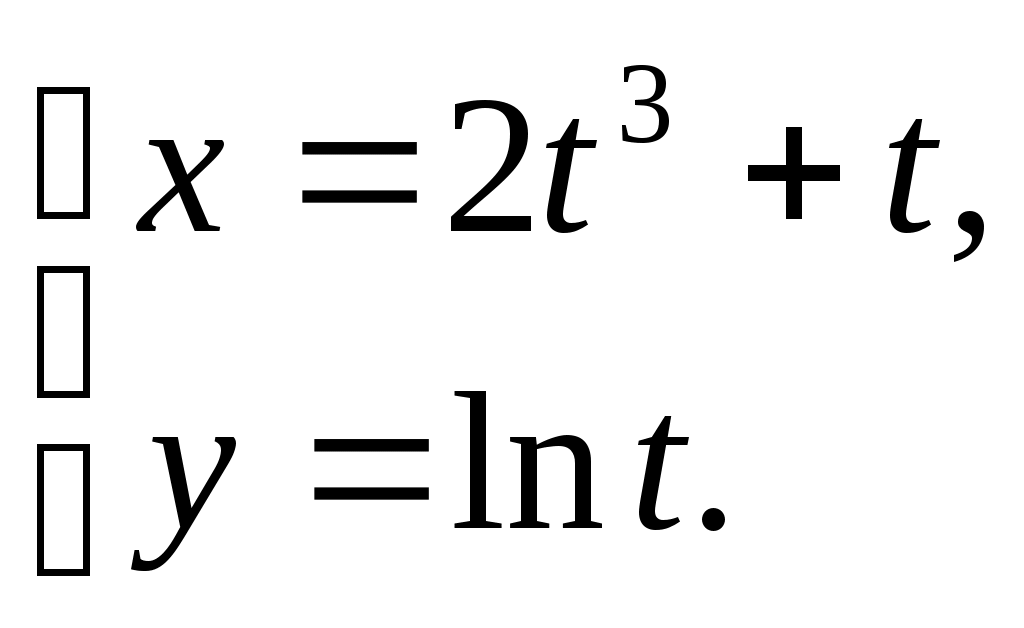

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   
7. 
   ,
   
8. 
   ,
   
9. 
   ,
   
10. 
    ,
    
11. 
    ,
    
12. 
    .
    

2. Найти :

1. 
   ,
   
2. 
   ,
   
3. 
   
   

3. Найти :



4. Найти дифференциал функции:



5. Составить уравнения касательной и нормали к линии в точке с абсциссой .