Домашнее задание. 1. Между населёнными пунктами A, B, C, D, E, f построены дороги, протяжённость которых приведена в таблице
 Скачать 65.83 Kb. Скачать 65.83 Kb.
|
|
1. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам). 2. На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. 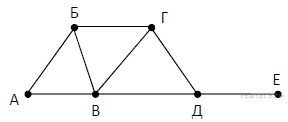
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину пути из пункта Б в пункт В, если передвигаться можно только по указанным дорогам. В ответе запишите целое число — длину пути в километрах. 3. Логическая функция F задаётся выражением ((y → x) ≡ (x → w)) ∧ (z ∨ x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. 4. Логическая функция F задаётся выражением: (¬x ∧ y ∧ z) ∨ (¬x ∧ y ∧ ¬z) ∨ (¬x ∧ ¬y ∧ ¬z). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу, затем – буква, соответствующая второму столбцу, и т. д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. 5. Даны фрагменты двух таблиц из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. На основании имеющихся данных определите ID человека, у которого в самом молодом возрасте появился первый правнук или правнучка. При вычислении ответа учитывайте только информацию из приведённых фрагментов таблиц.
6. Ниже представлены два фрагмента таблиц из базы данных о жителях микрорайона. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. Определите на основании приведённых данных, сколько жителей родились в том же городе, что и хотя бы один из их дедушек или хотя бы одна из их бабушек. При вычислении ответа учитывайте только информацию из приведённых фрагментов таблиц.
7. Для кодирования букв X, Е, Л, О, Д решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ЛЕДОХОД таким способом и результат запишите шестнадцатеричным кодом. 8. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали кодовые слова 100, 101, 00, 01 соответственно. Для двух оставшихся букв — Д и Е — коды неизвестны. Укажите кратчайшее кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений. 9. На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом. 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1001 числа 9 будет преобразована в 100111. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма. Укажите минимальное число N, для которого результат работы алгоритма будет больше 115. В ответе это число запишите в десятичной системе счисления. 10. Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 15. Система команд Кузнечика: Вперед 17 – Кузнечик прыгает вперёд на 17 единиц, Назад 6 – Кузнечик прыгает назад на 6 единиц. Какое наименьшее количество раз должна встретиться в программе команда «Назад 6», чтобы Кузнечик оказался в точке 36? 11. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, 3, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Л, но не проходящих через город Е? 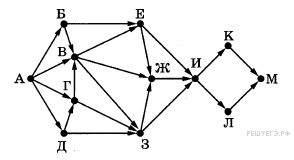 12. На рисунке представлена схема дорог. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город Г и НЕ проходящих через город З? 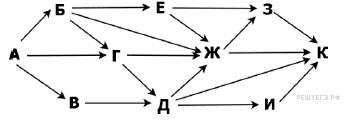 |
