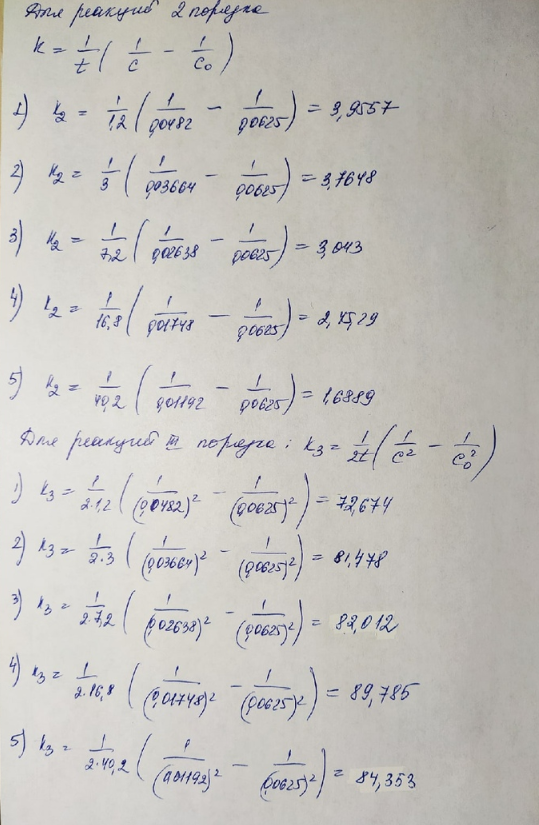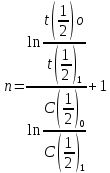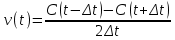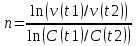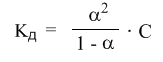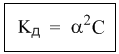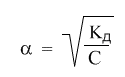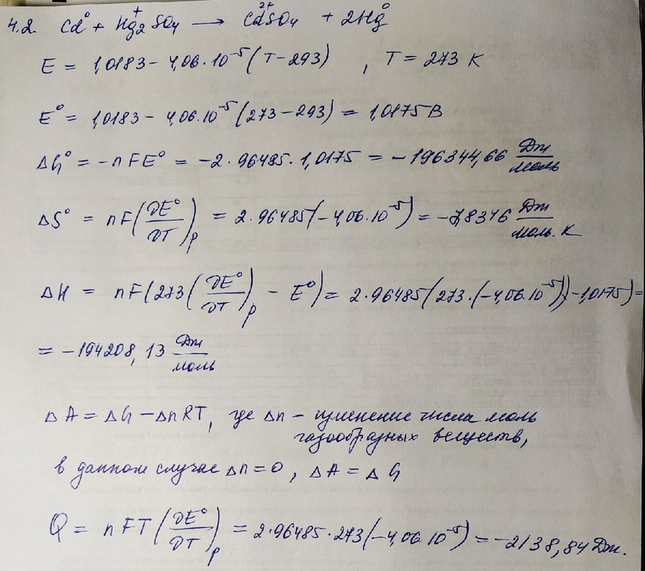|
|
Физическая химия. 1. Метод подбора уравнения
3.1
 
1.Метод подбора уравнения.

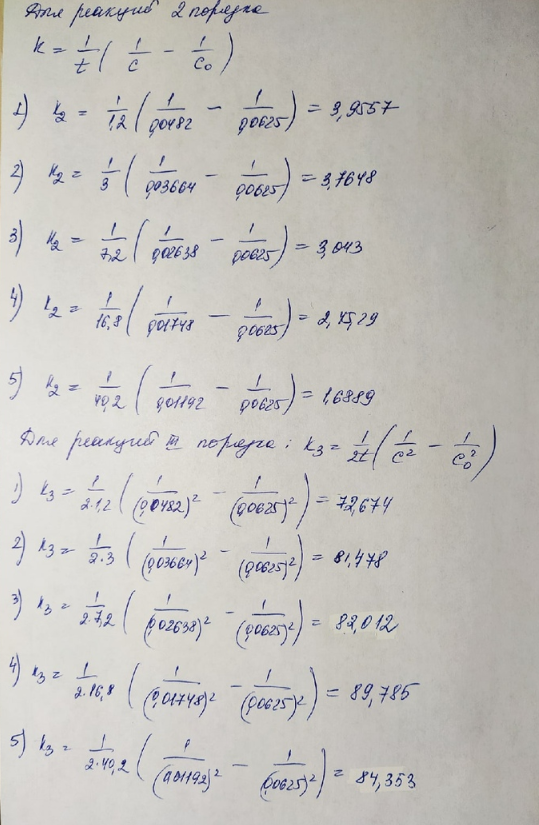
Значения констант скорости более однородны в случае реакции третьего порядка.
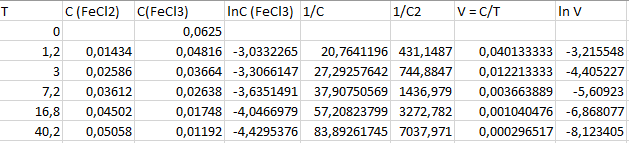
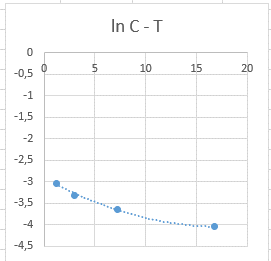
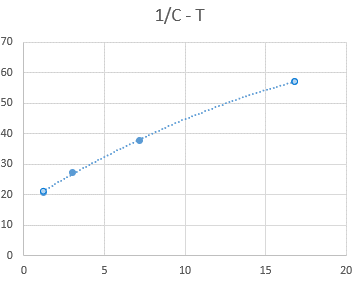
2.Графический метод: построение графиков и определение, какая зависимость линейна.
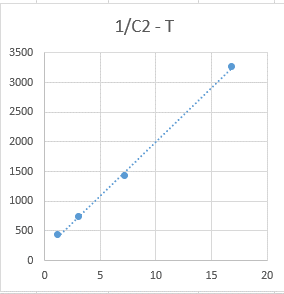
Зависимость 1/С2 от Т более линейна, что говорит о том, что данная реакция – реакция третьего порядка.
3.Метод Оствальда-Нойеса
Способ определения порядка реакции на основании зависимости времени превращения исходного вещества на определенную долю x (t1/x) от начальной концентрации. Использование интегрального кинетического уравнения n-го порядка позволяет в этом случае получить соотношение

Если известен большой массив данных одного опыта, можно оценить время t1/x , соответствующее различным значениям x (x=2, 3, 4…) Численные значения отношений 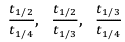 также зависят от порядка реакции. также зависят от порядка реакции.
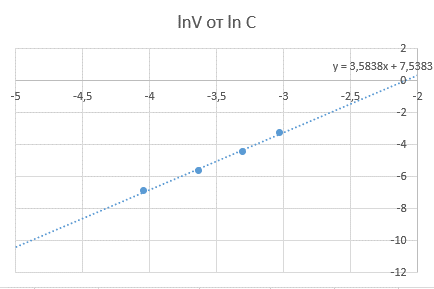
Задаемся двумя «начальными» концентрациями: С0 = -3, С1 = -4. Затем по графику определяем промежутки времени, за которые «первая» концентрация уменьшится в два раза и станет равной соответственно С(1/2)0 = -6 и С(1/2)1 = -8.
Получим t(1/2)0 -13,96, t(1/2)1
-21,1321
Тогда порядок реакции
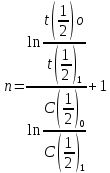
n = (ln(-13,96/-21,1321)/ (ln(-6/-8) +1 = 2,44
4.Дифференциальный метод Вант-Гоффа.
Метод Вант-Гоффа основан на численном определении скорости реакции, которое возможно при переходе от бесконечно малых приращений концентрации и времени к конечным приращениям. Записывается приближенное выражение для каждого интервала времени протекания реакции, причем она тем точнее, чем меньший промежуток времени рассматривается.
При аналитической форме решения рассматривается скорость реакции для двух интервалов времени. Разделив полученные выражения друг на друга и прологарифмируя полученное выражение, оценивают порядок реакции. При графическом варианте - уравнение скорости приводят к линейной форме. Экспериментально устанавливаются концентрации вещества в разные моменты времени по ходу проведения реакции. График, построенный в координатах «логарифм средней скорости протекания реакции - средние концентрации реагирующего вещества» на данном интервале времени представляет собой прямую линию. Тангенс угла наклона этой прямой равен порядку химической реакции n.
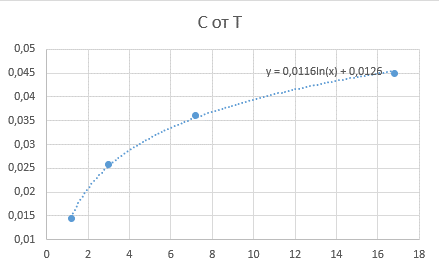
Взяты две точки на графике. Временной промежуток = 2 (берется любой удобный промежуток)
t1 =7,2
С1 = 0,02638
Δt1 = 2
Тогда
C(t1-Δt1) = C(5,2) = 0,0116ln(5,2) + 0,0126 = 0,03172
C(t1+Δt1) = C(9,2) = 0,0116ln(9,2) + 0,0126 = 0,03834
t2 = 3
С2 = 0,03664
Δt2 = 2
Тогда
C(t2-Δt2) = C(1) = 0,0136
C(t2+Δt2) = C(5) = 0,0116ln(5) + 0,0126 = 0,03127
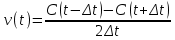
v(t1) = (0,03172-0,03834)/(2*2) = - 0,001655
v(t2) = (0,0136-0,03127)/(2*2) = -0,0044
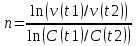
n = ln(-0,001655/-0,0044)/ln(0,0238/0,03664) = -0,9778/-0,4315 = 2,27
3.3


4.1


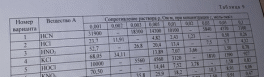
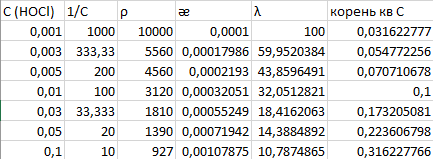
 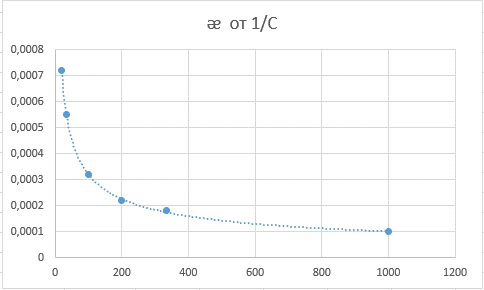


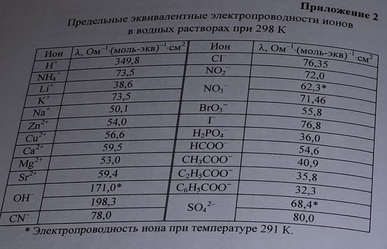
Хлорноватистая кислота – слабый электролит, закон Кольрауша не выполняется.
Для бинарного электролита предельная электропроводность равна алгебраической сумме предельных подвижностей аниона и катиона:
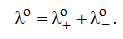
Значения предельных подвижностей являются важными характеристиками ионов. Они приведены в соответствующих таблицах.
В справочных данных (методичка и другие справочники) отсутствует подвижность гипохлорит-аниона ClO-. Рассчитать электропроводность при бесконечном разбавлении не представляется возможным.
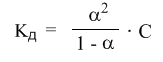
Это математическая формулировка закона разбавления Оствальда. Закон Оствальда справедлив для бинарных электролитов, т.е. веществ, молекулы которых в растворе распадаются на два иона – катион и анион. В случае сильных электролитов, когда α близка к 1, знаменатель дроби стремится к нулю, а константа диссоциации Кд – к бесконечности.
Однако в случае слабых электролитов величина (1 – α) очень мало отличается от единицы. Действительно, если α = 0,01, то (1 – 0,01) = 0,99, т.е. практически 1. Таким образом, для слабых электролитов закон разбавления Оствальда можно записать в более простом виде:
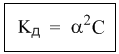
Для хлорноватистой кислоты константа диссоциации равна K = 2,95·10-8
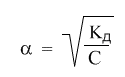
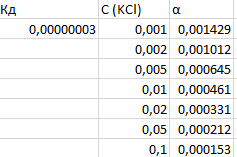
При разбавлении степень диссоциации слабого электролита растет. Закон Оствальда выполняется.
4.2


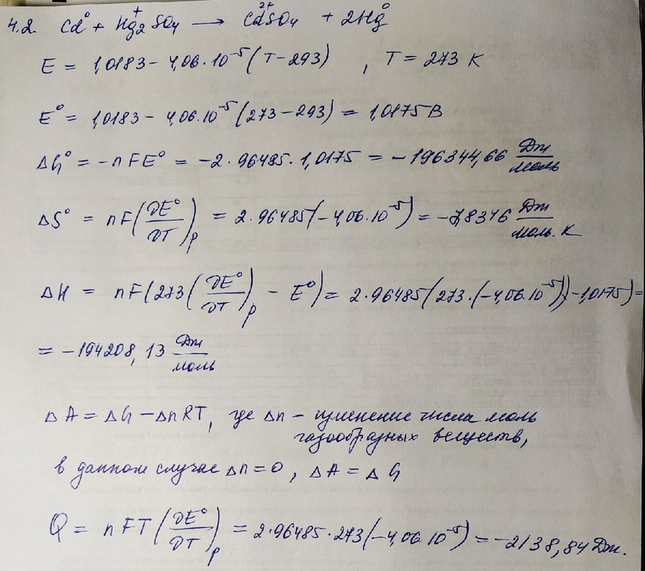 |
|
|
 Скачать 4.08 Mb.
Скачать 4.08 Mb.