математика. Построение графиков функции геометрическими преобразованиями

• Название: Построение графиков функции геометрическими преобразованиями
• Анкор: математика
• Дата: 20.10.2021
• Размер: 77.1 Kb.
• Имя файла: Smirnykh_Matematika.docx
• Тип: Реферат; #251657

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ индустриальный университет» Тобольский индустриальный институт (филиал)

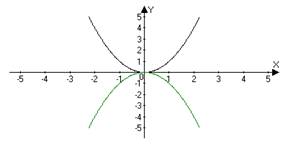
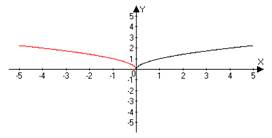
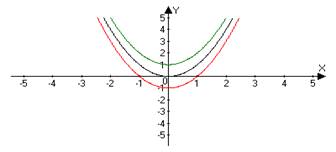
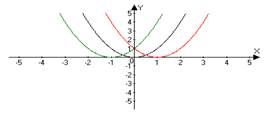
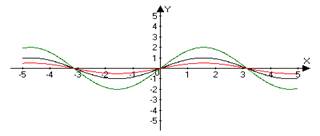
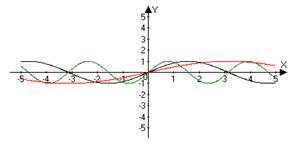
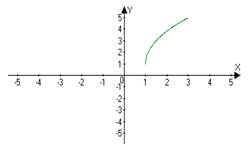
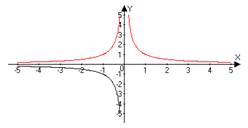
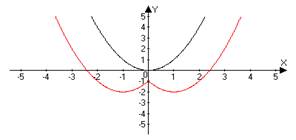
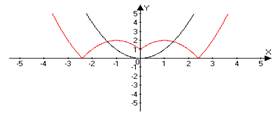
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
Построение графиков функции геометрическими преобразованиями
Смирных Андрей Алексеевич, КИПр-17-(9)-1

(ФИО автора – разработчика, профессия, группа)
Яковых Оксана Владимировна, преподаватель, к.п.н

(ФИО руководителя, должность, звания)

Согласовано:
(А.А. Смирных) автор - разработчик проекта _________________________
(О.В. Яковых) руководитель проекта ________________________________
Итоговая оценка за «Индивидуальный проект» ____________________________
Дата «____»___________ 2018 г.
Тобольск, 2018

Содержание

Введение 3

Глава 1.История возникновения функции 4

Глава 2. Основные понятия о функциях 6

Глава 3. Построение графиков функции геометрическими преобразованиями...................................................................................................7

Заключение 12

Список использованной литературы 13


Введение

Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решить многие задачи и парой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес.

Цель: Изучить построение графиков функции геометрическими преобразованиями.

Задачи:

1. Изучить теоретический материал по теме исследования.

2. Рассмотреть примеры построения графиков геометрическими преобразованиями.


Глава 1. История возникновения функции
Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что, чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем дольше горит костер, тем теплее будет в пещере. С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами. Многие из них выражались с помощью чисел. Это позволило формулировать их словами "больше на", "меньше на", "больше во столько-то раз". Если за одного быка давали 6 овец, то двух быков обменивали на 12 овец, а трех быков на 18 овец. Такие расчеты привели к возникновению понятия о пропорциональности величин.

Вклад в развитие графиков функций Рене Декартом.

Чтобы создать математический аппарат для изучения графиков функций, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, он разрушил пропасть, лежавшую со времен древнегреческой математики, между геометрией и арифметикой.

Чтобы освободить алгебру от несвойственного ей геометрического языка, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему.

При записи зависимостей между величинами Декарт стал применять буквы. При этом операциями над величинами соответствовали операции над буквами. Теперь уже для преобразования одной зависимости в другую не надо было писать громоздких пропорций, изучать подобные треугольники и преобразовывать геометрические фигуры. Достаточно было по твердо, установленным правилам делать алгебраические преобразования, причем все эти преобразования производились в общем, виде. Таким образом, графики функций за все время своего существования прошли через ряд фундаментальных преобразований, приведших их к тому виду, к которому мы привыкли. Каждый этап или ступень развития графиков функций - неотъемлемая часть истории современной алгебры и геометрии.

Глава 2. Основные понятия о функциях.
Величины, участвующие в одном и том же явлении, могут быть взаимосвязаны, так что изменение одних из них влечёт за собой соответствующее изменение других. Например, увеличение (или уменьшение) радиуса круга ведёт к обязательному увеличению (или уменьшению) его площади. В таких случаях говорят, что между переменными величинами существует функциональная зависимость, причём одну величину называют функцией, или зависимой переменной (е часто обозначают буквой у), а другую - аргументом, или независимой переменной (её обозначают буквой х). Функциональную зависимость между х и у принято обозначать символом y=f (x). Если значению х соответствует больше, чем одно значение у. то такая функция называется многозначной. Исследование многозначных функций обычно сводится к исследованию однозначных.

Переменная величина у есть функция аргумента х, т.е. y=f (x), если каждому возможному значению х соответствует одно определённое значение у.

Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f (x). Горизонтальную ось Ох называют осью абсцисс, вертикальную ось Оу - осью ординат. Графическое изображение функции имеет важное значение для её изучения. На графике функции часто непосредственно видны такие её особенности, которые можно было бы установить лишь путём длительных вычислений. Если между величинами х и у существует функциональная связь, то безразлично, какую из этих величин считать аргументом, а какую - функцией.
Глава 3. Построение графиков функции геометрическими преобразованиями.

№	Функция	Преобразование	Графики
1	y = −f(x)	Сначала строим график функции f(x), а затем симметрично отображаем его относительно оси OX.	y = − (x2) y = x2 → − (x2)
2	y = f(−x)	Сначала строим график функции f(x), а затем симметрично отображаем его относительно оси OY.	y = √ (−x) y =√(x) → √ (−x)
3	y = f(x) +A A - const	Сначала строим график функции f(x), а затем, если А>0 поднимаем полученный график на А единиц вверх по оси OY. Если А<0, то опускаем вниз.	y = x2 → x2 +1 y = x2 → x2 –1
4	y = f(x −а)	Сначала строим график функции f(x), а затем, если а>0, то график функции смещаем на а единиц вправо, а если а<0, то на а единиц влево. "−" − → "+" − ←	y = x2 → (x + 1)2 y = x2 → (x -1)2
5	y = K f(x ) k − const k>0	Сначала строим график функции f(x), а затем, если K>0, то растягиваем полученный график в K раз вдоль оси OY. А если 0< K<1, то сжимаем полученный график в 1 ∕ K раз вдоль оси OY. ↕ ↓ ↑	y = sin(x) → 2sin(x) y = sin(x) → Ѕ sin(x)
6 7	y = f(к x ) k − const k>0 y = A ѓ(к x+а) +В A, к, а, В − const	Сначала строим график функции f(x), а затем, если к >1, то сжимаем полученный график в к раз вдоль оси OХ. А если 0< к <1, то растягиваем полученный график в 1∕ к раз вдоль оси OХ. к >1 − →← 0< к <1 − ←→ f( x ) → f(к x ) → f(к( х + а ∕ к )) →A f(к( х + а ∕ к )) → A f(к( х + а ∕ к )) +В	y = sin(x) → sin(2x) y = sin(x) → sin (Ѕ x)     y = 2√(2x-2)+1 y =√x →√2x→√2(x -1) → 2√2(x -1) →2√2(x-1)+1
8	y = │f(x)│	Сначала строим график функции ѓ(x), а затем часть графика, расположенную выше оси ОХ оставляем без изменения, а часть графика, расположенную ниже оси ОХ, заменяем симметричным отображением относительно ОХ.	y =│x3│ y = x3→│x3│
9	y = f(│x│)	Сначала строим график функции f(x), а затем часть графика, расположенную правее оси ОУ, оставляем без изменения, а левую часть графика заменяем симметричным отображением правой относительно ОУ.	y = (│x│−1)2 −2 y = x2→(x -1)2→ (x -1)2 − 2→(│x│−1)2 −2
10	y = │f(│x│)│	f(x) → f(│x│) →│f(│x│)│	y= │(│x│−1)2 - 2│ y= x2 → (x-1)2 →(x-1)2 - 2→(│x│−1)2 - 2→│(│x│−1)2 - 2│

Заключение

Графики функций выходят далеко за пределы курса математики. Во многих профессиях пригодится умение читать графики. На протяжении многих веков учёные постепенно приходили к тому определению функции, которое мы изучаем.

Мы изучили графики функции с геометрическим преобразованием и рассмотрели примеры их построения.


Список используемой литературы

1. Виленкин Н.Я., "Функции в природе и технике", М., 1978;
2. Сивашинский И.Х., "Элементарные функции графики", М., 1965;
3. Дронов А.М., "Графики функций", М., 1972;

4. Режим доступа: https://otherreferats.allbest.ru/mathematics/00489947_0.html. Дата обращения: 26.12.2018г.