1 Методы анализа сложных электрических цепей

• Название: 1 Методы анализа сложных электрических цепей
• Дата: 24.10.2022
• Размер: 70.24 Kb.
• Имя файла: 1.4расчёт.docx
• Тип: Задача; #751735

1.4. Методы анализа сложных электрических цепей.

В электротехнике рассматривается устройство и принцип действия основных электротехнических устройств, используемых в быту и промышленности. Чтобы электротехническое устройство работало, должна быть создана электрическая цепь, задача которой передать электрическую энергию этому устройству и обеспечить ему требуемый режим работы.

Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении.

Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения. Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры, представлена на рис. 1.4.1.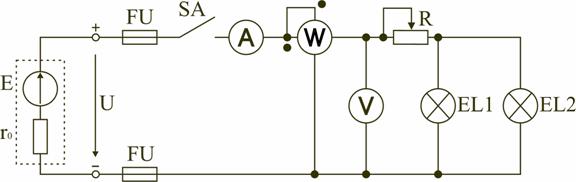



Рис. 1.4.1

Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы:

1) Источники электрической энергии (питания).

Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками. Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства).

2) Потребители электрической энергии.

Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор). Иногда потребители называют нагрузкой.

3) Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает.

Все элементы цепи охвачены одним электромагнитным процессом.

В электрической схеме на рис. 1.4.1 электрическая энергия от источника ЭДС E, обладающего внутренним сопротивлением r₀, с помощью вспомогательных элементов цепи передаются через регулировочный реостат R к потребителям (нагрузке): электрическим лампочкам EL₁ и EL₂.

Основные понятия и определения для электрической цепи

Для расчета и анализа реальная электрическая цепь представляется графически в виде расчетной электрической схемы (схемы замещения). В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают. Источник питания показывается как источник ЭДС E с внутренним сопротивлением r₀, реальные потребители электрической энергии постоянного тока заменяются их электрическими параметрами: активными сопротивлениями R₁, R₂,…,R_n. С помощью сопротивления R учитывают способность реального элемента цепи необратимо преобразовывать электроэнергию в другие виды, например, тепловую или лучистую.

При этих условиях схема на рис. 1.4.1 может быть представлена в виде расчетной электрической схемы (рис. 1.4.2), в которой есть источник питания с ЭДС E и внутренним сопротивлением r₀, а потребители электрической энергии: регулировочный реостат R, электрические лампочки EL₁ и EL₂ заменены активными сопротивлениями R,R₁ и R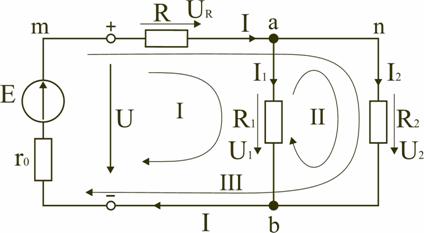₂.

Рис. 1.4.2

Источник ЭДС на электрической схеме (рис. 1.4.2) может быть заменен источником напряжения U, причем условное положительное направление напряжения U источника задается противоположным направлению ЭДС.

При расчете в схеме электрической цепи выделяют несколько основных элементов.

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Схема на рис. 1.4.2 имеет три ветви: ветвь bma, в которую включены элементы r₀,E,R и в которой возникает ток I; ветвь ab с элементом R₁ и током I₁; ветвь anb с элементом R₂ и током I₂.

Узел электрической цепи (схемы) – место соединения трех и более ветвей. В схеме на рис. 1.4.2 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R₁ и R₂ (рис. 1.4.2) находятся в параллельных ветвях.

Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 1.4.2 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура.

Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах. На схеме (рис. 1.4.2) стрелками укажем положительные направления ЭДС, напряжений и токов:

а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу;

б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно;

в) для напряжений – совпадающими с направлением тока в ветви или элемента цепи.

Все электрические цепи делятся на линейные и нелинейные.

Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от тока в нем, называют линейным, например электропечь.

Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.

Следовательно, в линейной электрической цепи все элементы – линейные, а нелинейной называют электрическую цепь, содержащую хотя бы один нелинейный элемент.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

 ,

где n – число источников ЭДС в контуре;

m – число элементов с сопротивлением R_k в контуре;

U_k=R_kI_k – напряжение или падение напряжения на k-м элементе контура.

Для схемы (рис. 1.4.2) запишем уравнение по второму закону Кирхгофа:

E=U_R+U₁.

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС равна нулю

 .

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 1.2):

контур I: E=RI+R₁I₁+r₀I,

контур II: R₁I₁+R₂I₂=0,

контур III: E=RI+R₂I₂+r₀I.

В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия

W=I²Rt.

Скорость преобразования электрической энергии в другие виды представляет электрическую мощность

 .

Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.

 . (*)

Это соотношение называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение EI подставляют в (*) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение EI подставляют в (*) со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:

EI=I²(r₀+R)+I₁²R₁+I₂²R₂.

При расчете электрических цепей используются определенные единицы измерения. Электрический ток измеряется в амперах (А), напряжение – в вольтах (В), сопротивление – в омах (Ом), мощность – в ваттах (Вт), электрическая энергия – ватт-час (Вт-час) и проводимость – в сименсах (См)

Кроме основных единиц используют более мелкие и более крупные единицы измерения: миллиампер (1 мA = 10^–3 А), килоампер (1 кA = 10³ А), милливольт (1 мВ = 10^–3 В), киловольт (1 кВ = 10³ В), килоом (1 кОм = 10³ Ом), мегаом (1 МОм = 10⁶ Ом), киловатт (1 кВт = 10³ Вт), киловатт-час (1 кВт-час = 10³ ватт-час).

Расчет разветвленной электрической цепи с несколькими источниками питания

Основным методом расчета является метод непосредственного применения первого и второго законов Кирхгофа.

В качестве примера рассмотрим цепь, схема которой приведена на рис. 1.4.3. Схема цепи содержит 6 ветвей (m=6) и 4 узла: a, b, c, d (n=4). По каждой ветви проходит свой ток, следовательно число неизвестных токов равно числу ветвей, и для определения токов необходимо составить m уравнений. При этом по первому закону Кирхгофа составляют уравнения для (n–1) узлов. Недостающие m–(n–1) уравнения получают по второму закону Кирхгофа, составляя их для m–(n–1) взаимно независимых контуров. Рекомендуется выполнять операции расчета в определенной последовательности.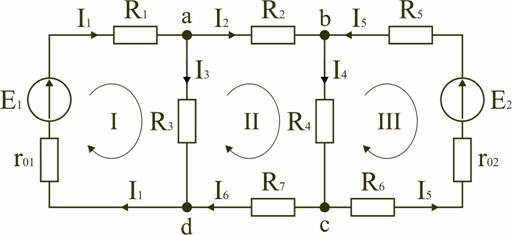

Рис. 1.4.3

1. Обозначение токов во всех ветвях. Направление токов выбираем произвольно, но в цепях с источниками ЭДС рекомендуются, чтобы направление токов совпадало с направлением ЭДС.

2. Составление уравнений по первому закону Кирхгофа. Выбираем 4–1=3 узла (a, b, c) и для них записываем уравнения:

узел a: I₁−I₂−I₃=0;

узел b: I₂−I₄+I₅=0;

узел c: I₄−I₅+I₆=0.

3. Составление уравнений по второму закону Кирхгофа. Необходимо составить 6–3=3 уравнения. В схеме на рис. 1.4.3 выбираем контура I, II, III и для них записываем уравнения:

контур I: E₁=I₁(r₀₁+R₁)+I₃R₃;

контур II: 0=I₂R₂+I₄R₄+I₆R₇−I₃R₃;

контур III: −E₂=−I₅(r₀₂+R₅+R₆)−I₄R₄.

4. Решение полученной системы уравнений и анализ результатов. Полученная система из шести уравнений решается известными математическими методами. Если в результате расчетов численное значение тока получено со знаком «минус», это означает, что реальное направление тока данной ветви противоположно принятому в начале расчета. Если в ветвях с ЭДС токи совпадают по направлению с ЭДС, то данные элементы работают в режиме источников, отдавая энергию в схему. В тех ветвях, где направления тока и ЭДС не совпадают, источники ЭДС работает в режиме потребителя.

5. Проверка правильности расчетов. Для проверки правильности произведенных расчетов можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы уравнений:

узел d: I₃+I₆−I₁=0

внешний контур схемы: E₁−E₂=I₁(r₀₁+R₁)+I₂R₂−I₅(r₀₂+R₅+R₆)+I₆R₇.

Независимой проверкой является составление уравнения баланса мощностей (*) с учетом режимов работы элементов схемы с ЭДС:

 .

Если активная мощность, поставляемая источниками питания, равна по величине активной мощности, израсходованной в пассивных элементах электрической цепи, то правильность расчетов подтверждена.

Метод узлового напряжения

Этот метод рекомендуется использовать в том случае, если сложную электрическую схему можно упростить, заменяя последовательно и параллельно соединенные резисторы эквивалентными, используя при необходимости преобразование треугольника сопротивлений в эквивалентную звезду. Если полученная схема содержит несколько параллельно соединенных активных и пассивных ветвей, то ее расчет и анализ весьма просто можно произвести методом узлового напряжения.

Метод эквивалентного генератора

Метод эквивалентного генератора позволяет произвести частичный анализ электрической цепи. Например, определить ток в какой-либо одной ветви сложной электрической цепи и исследовать поведение этой ветви при изменении ее сопротивления. Сущность метода заключается в том, что по отношению к исследуемой ветви amb сложная цепь заменяется активным двухполюсником А, схема замещения которого представляется эквивалентным источником (эквивалентным генератором) с ЭДС E_э и внутренним сопротивлением r_0э, нагрузкой для которого является сопротивление R ветви amb.