|
|
Условные положительные направления эдс, токов, напряжений
   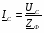  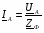 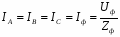 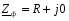 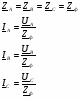  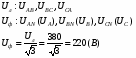 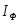 Условные положительные направления ЭДС, токов, напряжений. Условные положительные направления ЭДС, токов, напряжений.
Для проведения расчета и анализа электрических цепей необходимо знать не только значения заданных ЭДС, напряжений или токов, но и их направления, так как последние определяют знаки слагаемых в расчетных выражениях. В связи с этим следует напомнить о направлениях токов, напряжений и ЭДС, принятых в физике.
За направление тока принимают направление движения положительных зарядов.
За направление напряжения между какими-либо точками электрической цепи принимают напревление, в котором перемещались бы положительные заряды между этими точками под действием сил электрического поля, т. е. от большего потенциала к меньшему.
За направление ЭДС между выводами источника или активного приемника принимают направление, в котором перемещались бы положительные заряды под действием сил стороннего поля, т. е. от меньшего потенциала к большему.
Так, в электрической цепи рис. 1.1, а потенциал точки а больше потенциала точки b (φа > φb), поэтому напряжение направлено от точки а к точке b, а ЭДС Е — от точки b к точке а.
На участке атb, содержащем пассивные элементы, положительные заряды перемещаются под действием сил электрического поля от большего потенциала к меньшему; направления напряжения и тока на этом участке совпадают. На участке bпа, содержащем источник электрической энергии, положительные заряды перемещаются под действием ЭДС от меньшего потенциала к большему, направление тока на таком участке совпадает с направлением ЭДС и противоположно направлению напряжения.
Для удобства дальнейшего изложения будем называть указанные выше направления действительными направлениями.
Расчет и анализ любых электрических цепей может быть произведен с помощью основных законов электрических цепей: закона Ома, первого и второго законов Кирхгофа. Указанные законы используются также для обоснования различных методов, упрощающих расчет и анализ цепей.
Запись выражении по законам Ома и Кирхгофа, различных методов расчета и анализа, а также расчетных формул производится с учетом определенных направлений как заданных величин (например, ЭДС, напряжений или токов), так и величин, подлежащих определению.
При расчете и анализе электрических цепей направления заданных и искомых величин указывают на схемах стрелками, считают их положительными (Е > 0, U > 0 и I > 0) и поэтому называют положительными направлениями.
За положительные направления заданных и искомых величин при постоянном токе принимают их действительные направления. Если они не очевидны, можно задаться положительными направлениями произвольно, так как от выбора тех или иных положительных направлений зависят лишь знаки искомых величин, а не их значения.
В качестве положительных направлений величин, изменяющих свои действительные направления с течением времени, например при расчете или анализе цепей переменного тока, задают одно из двух возможных их направлений, с учетом которого и производят расчет.
Если в результате расчета или анализа какая-либо из искомых величин оказывается положительной, это означает, что она направлена в действительности так, как показано на схеме стрелкой; отрицательное значение искомой величины указывает на ее противоположное направление. Сказанное относится и к величинам, действительные направления которых с течением времени изменяются.
В книге используется Международная система единиц (СИ), в которой основной единицей ЭДС, напряжения и потенциала является 1 вольт (1 В). Кроме единицы 1 вольт в практике используется единица 1 киловольт (1 кВ = 103 В) и 1 милливольт (1 мВ = 10-3 В).
Основной единицей тока является 1 ампер (1 А). Для тока используются также единицы 1 миллиампер (1 мА = 10-3 А) и 1 микроампер (1 мкА = 10-6 А).
|
2 Последовательное и параллельное соединения элементов электрических цепей и их свойства.
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: 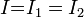
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: 
Резисторы


Катушка индуктивности

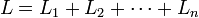
Электрический конденсатор

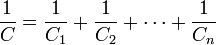
Параллельное соединение
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках: 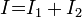
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: 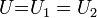
Резистор
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 1/R складывается из проводимостей каждого резистора 1/Ri)
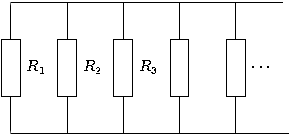
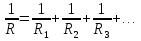
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее(искомое) сопротивление.
Электрический конденсатор


|
Расчет разветвленных цепей методом эквивалентных преобразований.
Эквивалентным называется преобразование, при котором напряжение и токи в частях схемы, не подвергшихся преобразованию, не меняются.
При расчетах сложных электрических цепей во многих случаях целесообразно производить их упрощение путем свертывания, заменяя отдельные участки цепи с последовательным, параллельным и смешанным соединениями сопротивлений одним эквивалентным сопротивлением с помощью метода эквивалентных преобразований (метода трансфигураций) электрических цепей.
Электрическая цепь с последовательным соединением сопротивлений (рис. 1.2) заменяется при этом цепью с одним эквивалентным сопротивлением (рис. 1.3), равным сумме всех сопротивлений цепи: 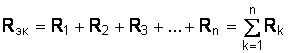 , где – сопротивления отдельных участков цепи. , где – сопротивления отдельных участков цепи.
 Рис. 1.2. Последовательное соединение сопротивлений Рис. 1.2. Последовательное соединение сопротивлений
 Рис. 1.3. Эквивалентная схема замещения Рис. 1.3. Эквивалентная схема замещения
При этом ток I в электрической цепи сохраняет неизменным свое значение, все сопротивления обтекаются одним и тем же током. Напряжения (падения напряжения) на сопротивлениях при их последовательном соединении распределяются пропорционально сопротивлениям отдельных участков: 
При параллельном соединении сопротивлений все сопротивления находятся под одним и тем же напряжением U (рис. 1.4). Электрическую цепь, состоящую из параллельно соединенных сопротивлений, целесообразно заменить цепью с эквивалентным сопротивлением , которое определяется из выражения, где 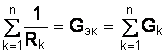 – сумма величин, обратных сопротивлениям участков параллельных ветвей электрической цепи (сумма проводимостей ветвей цепи); – сопротивление параллельного участка цепи; – эквивалентная проводимость параллельного участка цепи, ; n – число параллельных ветвей цепи. – сумма величин, обратных сопротивлениям участков параллельных ветвей электрической цепи (сумма проводимостей ветвей цепи); – сопротивление параллельного участка цепи; – эквивалентная проводимость параллельного участка цепи, ; n – число параллельных ветвей цепи.
При параллельном соединении двух сопротивлений и эквивалентное сопротивление , а токи распределяются обратно пропорционально их сопротивлениям, при этом .
 Рис. 1.4. Параллельное Рис. 1.4. Параллельное
соединение сопротивлений
При смешанном соединении сопротивлений (рис. 1.5), т. е. при наличии участков электрической цепи с последовательным и параллельным соединением сопротивлений, эквивалентное сопротивление цепи определяется в соответствии с выражением
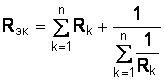 ; ; 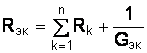 . .
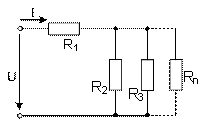 Рис. 1.5. Смешанное соединение сопротивлений Рис. 1.5. Смешанное соединение сопротивлений
Сущность метода заключается в том, чтобы сложную разветвленную цепь с помощью эквивалентных преобразований привести к простейшей одноконтурной цепи, включающей ветвь с искомым током, значение которого определяется затем по закону Ома. К эквивалентным преобразованиям относятся: а) преобразование представления источников электрической энергии*; б) замена последовательных и параллельных соединений однотипных элементов эквивалентными одиночными элементами; в) преобразование соединений «звезда»–«треугольник» и «треугольник»–«звезда».
Преобразование треугольника сопротивлений в эквивалентную звезду
Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если же заменить треугольник сопротивлений
R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.
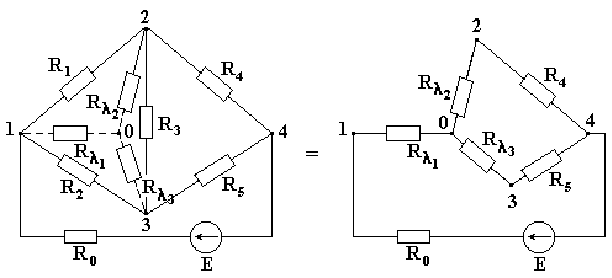 Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника. Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам: 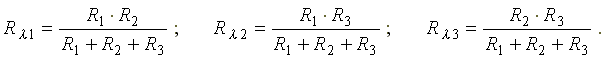
Эквивалентное соединение полученной схемы определяется по формуле
|
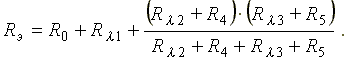
Сопротивления R0 и Rλ1 включены последовательно, а ветви с сопротивлениями Rλ1 + R4 и Rλ3 + R5 соединены параллельно.
2.4.Преобразование звезды сопротивлений в эквивалентный треугольник
Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений RΔ1-RΔ2-RΔ3, включенных между узлами 1-2-3.
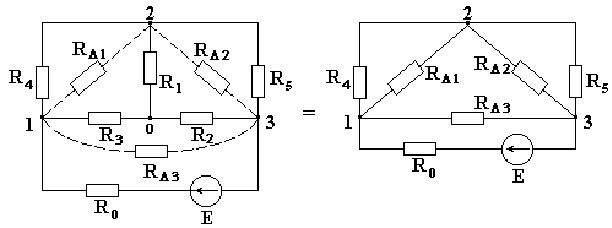
2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник
Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:
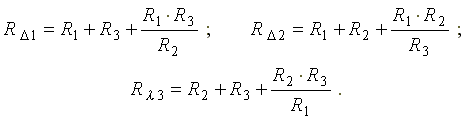
Эквивалентное сопротивление преобразованной схемы равно
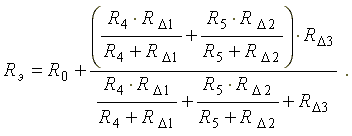
|
Расчет сложных электрических цепей на базе законов Кирхгофа.
В том случае, когда в разветвленной электрической цепи с несколькими источниками имеется группа активных или пассивных элементов, соединенных последовательно или параллельно, следует для упрощения расчета и анализа заменить их соответственно одним эквивалентным пассивным пли одним активным элементом. Иногда может показаться целесообразным использовать преобразование треугольника резистивных элементов в звезду.
Первый закон Кирхгофа – алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю 
Второй закон Кирхгофа – алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений в нем. 
Метод законов Кирхгофа. Используя первый и второй законы Кирхгофа, можно для любой разветвленной электрической цепи составить необходимое число независимых уравнений и путем их совместного решения найти все подлежащие определению величины, например токи. Решая совместно уравнения, можно установить также зависимость между какими-либо величинами: между током и ЭДС, между двумя токами и т. д
Перед составлением уравнений необходимо показать на схеме положительные направления известных и неизвестных величин. Сначала следует составить более простые уравнения по первому закону Кирхгофа, максимальное число которых должно быть на единицу меньше числа узловых точек. Недостающие уравнения следует составить по второму закону Кирхгофа. 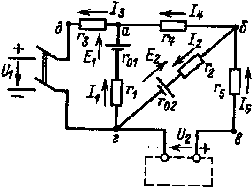 Рис, 1.13. К расчету разветвленных электрических цепей с помощью законов Кирхгофа Рис, 1.13. К расчету разветвленных электрических цепей с помощью законов Кирхгофа
В качестве примера составим схему уравнений для определения токов в электрической цепи, схема которой изображена на рис. 1.13. Будем считать, что ЭДС и напряжения с их направлениями, а также сопротивления известны. Поскольку данная цепь имеет пять ветвей с неизвестными токами, необходимо составить пять уравнений. Выбрав положительные направления токов I1, I2, I3, I4 и I5, для узлов а и б, а также для контуров агда, абга и бвгб при обходе последних по часовой стрелке получим.
I1 - I3 + I4 =0;
- I2 -I4 +I5 = 0;
- Е1 =- I1 (r1 +r01)- I3r3 - U1;
Е1 - Е2 = I1 (r1 + r01) + I2 (r2 + r02) - I4r4; Е2 == - I2 (r2 + r02) - I5r5 + U2.
| |
|
|
 Скачать 1.24 Mb.
Скачать 1.24 Mb.