|
|
Условные положительные направления эдс, токов, напряжений
5.Расчет сложных электрических цепей методом узлового напряжения.
В схеме произвольно выбирается опорный узел, обозначаемый “0”. Остальные узлы нумеруются от 1 до (q-1).
Узловые напряжения – это напряжения между каждым из (q-1) узлов и опорным с положительным направлением к опорному узлу.
Определив узловые напряжения, находят остальные, и далее, токи в ветвях по закону Ома.
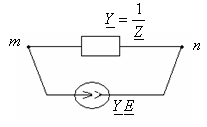
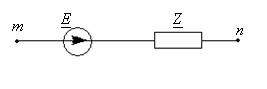
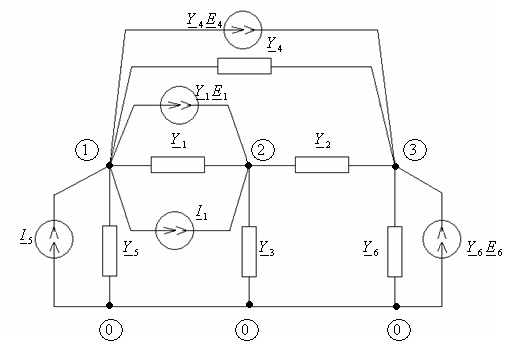
Алгоритм метода:
1.Производят эквивалентное преобразование ветвей с источниками ЭДС.
2.Уравнения метода записываются сразу в общем виде, исходя из числа узлов схемы относительно узловых напряжений.
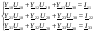
Собственная проводимость узлов – это сумма проводимостей ветвей, соединённых с данным узлом.
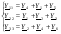
Общие проводимости узлов равны сумме проводимостей ветвей, соединяющих два узла, взятой со знаком “ – ”.
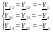
Правые части – это суммы токов источников тока, соединённых с данным узлом. При направлении источника к узлу он входит в сумму со знаком “ +”, в обратном случае – с “ - ”.
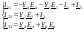
3/Решаем систему.
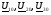 - ? - ?
4.Расчёт токов в ветвях по закону Ома. Положительное направление напряжения на ветви должно совпадать с положительным направлением тока в ветви.

Путь обоснования уравнений метода.
Выразить токи в ветвях через узловые напряжения по закону Ома. Затем подставить эти выражения токов в узловые уравнения. И упорядочить систему, считая неизвестными узловые напряжения.
|
6.Сложные цепи. Метод наложения
Метод наложения — метод расчёта электрических цепей, основанный на предположении, что ток в каждой из ветвей сложной электрической цепи при всех включённых источниках электрической энергии, равен алгебраической сумме токов в этой же ветви, полученных при включении каждого из генераторов по очереди и отключении остальных генераторов.Ток в любой ветви можно рассчитать как алгебраическую сумму токов, вызываемых в ней каждым источником электрической энергии в отдельности. При этом следует иметь ввиду, что когда ведут расчет токов, вызванных одним из источников электрической энергии, то остальные источники ЭДС в схеме замещают короткозамкнутыми участками, а источники тока разомкнутыми участками.
Данный метод позволяет существенно упростить расчеты сложных электрических цепей, содержащих небольшое количество источников электрической энергии.
Расчет сложных электрических цепей методом наложения производят в следующей последовательности:
Вычерчиваем принципиальную схему и все ее элементы.
Произвольно задаемся направлением токов всех ветвей и обозначаем их.
Определяем количество источников электрической энергии на схеме.
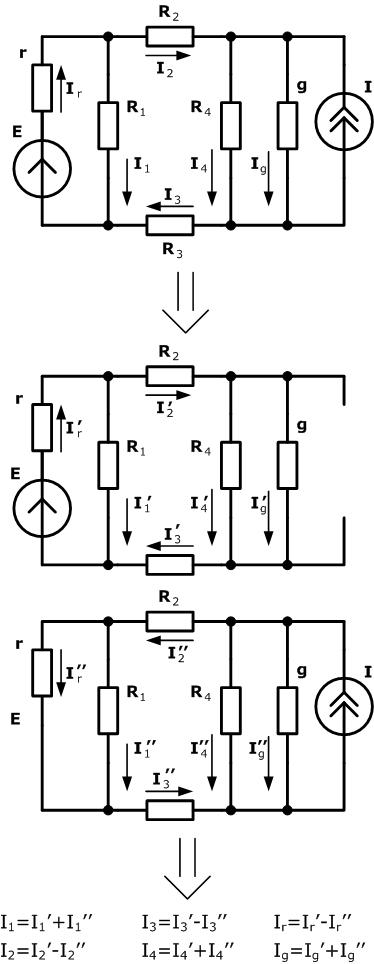
Для каждого источника электрической энергии вычерчиваем отдельную дополнительную схему, на которой выбранный источник отображаем без изменений (по сравнению с исходной схемой),а остальные источники замещаем (источники ЭДС на короткозамкнутый участок, источник тока на разомкнутый участок электрической цепи).
Для каждой из вновь вычерченной схемы обозначаем токи ветвей таким образом, чтобы не путать их с реальными токами ветвей исходной схемы (например если на исходной схеме ток ветви обозначен как I1, то на дополнительных схемах обозначаем его I1', I1'', I1''' и т.д.).
Рассчитываем каждую дополнительную схему в отдельности по методике расчета простых электрических цепей.
Определяем токи ветвей исходной схемы путем алгебраического суммирования токов ветвей всех дополнительных схем. Если направление тока на дополнительной схеме совпадает с направлением, указанным на основной схеме, ему присваивают знак "+", в противном случае присваивают знак "-
|
7.Синусоидальные ЭДС, ток, напряжение и их основные параметры. Действующее значение синусоидальных тока, ЭДС, напряжения.
Синусоидальные или гармонические величины математически описываются функциями вида: 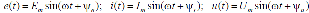
Где 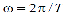 угловая частота функции с периодом T. В правой части выражений только одна величина является переменной – время t. Все остальные величины – константы. Значение функции в данный момент времени называется мгновенным значением и по соглашению обозначается строчной буквой. Кроме времени t, оно однозначно определяется тремя параметрами: амплитудой, угловой частотой или периодом и начальной фазой. Максимальное значение функции называется амплитудой или амплитудным значением и обозначается прописной буквой с индексом угловая частота функции с периодом T. В правой части выражений только одна величина является переменной – время t. Все остальные величины – константы. Значение функции в данный момент времени называется мгновенным значением и по соглашению обозначается строчной буквой. Кроме времени t, оно однозначно определяется тремя параметрами: амплитудой, угловой частотой или периодом и начальной фазой. Максимальное значение функции называется амплитудой или амплитудным значением и обозначается прописной буквой с индексом
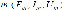
Аргумент синуса называется фазой, т.е. состоянием функции, а его значение в момент начала отсчёта времени(t=0)
начальной фазой (ψψ). Величину ,f=1/T, обратную периоду, называют частотой. Она связана с угловой частотой отношением: 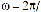
Амплитуды функций (2.1) измеряются в единицах, соответствующих величин, т.е. в вольтах и амперах. Период измеряется единицами измерения времени, а частота в герцах (1 Гц=1/c).
В цепях постоянного тока введение таких величин не требовалось, т.к. ЭДС, напряжения и токи были временными константами. На переменном токе вводится понятие действующего значения, как эквивалента теплового действия тока. По закону Джоуля-Ленца на участке электрической цепи с сопротивлением r, по которому протекает ток i, в течение элементарного промежутка времени dt выделится 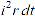 джоулей тепла, а за период T – джоулей тепла, а за период T – 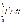 джоулей. Обозначим через I постоянный ток, при котором за тот же промежуток времени T в сопротивлении r выделится столько же тепла. Тогда: джоулей. Обозначим через I постоянный ток, при котором за тот же промежуток времени T в сопротивлении r выделится столько же тепла. Тогда: 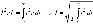 Величина I называется действующим, эффективным или среднеквадратичным значением переменного тока i. Подставляя выражение для синусоидального тока (2.1) и интегрируя, получим: Величина I называется действующим, эффективным или среднеквадратичным значением переменного тока i. Подставляя выражение для синусоидального тока (2.1) и интегрируя, получим:
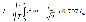 По аналогии определяются действующие значения напряжения и ЭДС: По аналогии определяются действующие значения напряжения и ЭДС: 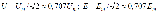 Понятие действующего значения очень широко используется в цепях переменного тока. Интегральной величиной, используемой в цепях переменного тока, является среднее значение Понятие действующего значения очень широко используется в цепях переменного тока. Интегральной величиной, используемой в цепях переменного тока, является среднее значение 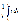 , т.е. площадь, ограниченная линией функции и осью времени на протяжении периода. Но для синусоидальных функций эта величина тождественно равна нулю, т.к. площади положительной и отрицательной полуволн равны по величине и противоположны по знаку. Поэтому условились под средним значением понимать среднее значение функции за положительный полупериод, т.е.: , т.е. площадь, ограниченная линией функции и осью времени на протяжении периода. Но для синусоидальных функций эта величина тождественно равна нулю, т.к. площади положительной и отрицательной полуволн равны по величине и противоположны по знаку. Поэтому условились под средним значением понимать среднее значение функции за положительный полупериод, т.е.:
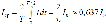 и аналогично для напряжения и ЭДC- и аналогично для напряжения и ЭДC- 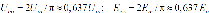
|
8.Представление синусоидальных величин векторами. Векторные диаграммы для цепей переменного тока.
Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью ω.
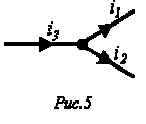
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
.
Каждый из этих токов синусоидален и может быть представлен уравнением
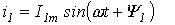 и и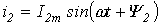 . .
Результирующий ток также будет синусоидален: 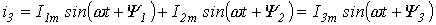 . .
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.
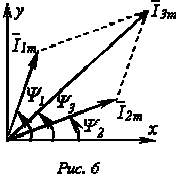 На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью ω их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным . На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью ω их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов: .
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: 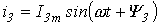 . .
|
Последовательное соединение элементов в цепи переменного тока.
Последовательное соединение элементов электрической цепи - это такое соединение, когда вывод одного элемента подключен к выводу другого элемента. В этом месте подключения нет узлов. Следующий элемент так же подключен к выводу другого элемента и т.д...
На рисунке ниже показано последовательное подключение 3 сопротивлений.
R1
U
I
R2
R3
+
U3
E
U2
U1
Формулы для расчета эквивалентного сопротивления при последовательном подключении элементов:
При последовательном подключении сопротивлений их эквивалентное сопротивление равно сумме сопротивлений.
Rэкв=ΣRi =R1 + R2 + R3 +...+Rn
При последовательном соединении индуктивностей их эквивалентное сопротивление равно сумме индуктивностей (без учета взаимной индуктивности).
Lэкв=ΣLi =L1 + L2 + L3 +...+Ln
При последовательном подключении емкостей обратная величина от эквивалентной емкости равна сумме обратных величин емкостей.
1/Сэкв =Σ(1/Ci )=1/С1+1/С2+1/С3+...+1/Cn
Свойства последовательного соединения элементов
При последовательном подключении элементов через них протекает одинаковый ток.
Согласно закону Ома и второму закону Кирхгофа экивалентное (суммарное) напряжение на участке последовательно соединенных сопротивлений равно сумме напряжений на каждом элементе. Uобщ= U1+U2+U3+U4 = I·(R1+R2+R3+R4). На данном принципе построены простейшие делители напряжения.
| |
|
|
 Скачать 1.24 Mb.
Скачать 1.24 Mb.