|
|
Условные положительные направления эдс, токов, напряжений
9. Элементы схем замещения цепей синусоидального тока: резистивный, индуктивный, емкостный.
Эл-ми схем замещ.цепей синусоид. I явл. ист-ки син-ных I и ЭДС (j(t), e(t)), резистивные (R), индуктивные (L) и емкостные (C) элементы. Они отн. к пасс.эл-там.
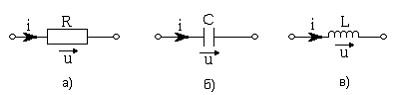
Рез. эл. (а) наз. такой эл., кот. обл. только сво-ом рассеив-я энергии. Матем-я модель рез. эл.R опред. з-ом Ома, кот. уст-ет зав-ть напр. u от тока i, протек-го через сопрот. R. Такую зав.наз. вольт-амперной хар-кой (ВАХ) рез-го эл-и запис- в след- виде:
u=iR или 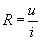
Вел, обр. сопр-ю, наз. проводимостью резистора. Она обозн. G и измер. в сименсах (См). ВАХ для лин.и нелин.рез. эл.:
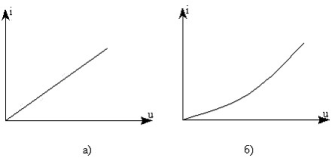
Мощность, рассеив. рез. эл-ом в виде тепла: 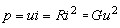
Инд. эл. (б) наз.такой эл. элект. цепи, кот. обл. только св-вом накопл-я энергии магн. поля. Матем. моделью инд.эл.L явл. вебер-амперная хар-ка, кот. уст-ет зав-ть суммарного магн. потока, образ-го в витках катушки, (потокосцепления ψ) от вел. протек. через кат. тока i. Уравн., опис. св-ва индукт.элем. им.вид: 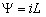
где w – число витков кат.; n – номер витка, с кот. сцеплен поток Фn, L – инд-ть .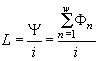
Согл. зак. эл-магн. инд. напряж. на индукт. элем. проп. скор. измен. тока в нем, т.е. 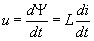
Емк. эл. (в) наз. эл. элек. цепи, облад.только св-вом накапл. эн.электр. поля. Матем. моделью емк. эл. С явл. вольт-кулоновая хар-ка, кот. устан. зав-сть напр. u от сообщенного емкости C электр. заряда q и опред. выр.: q=Cuили 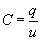
Мощность эл-их колеб-й в емк. элем. под дейст. запасен.в ней эн. к любому мом. врем. t опред. выр.: 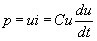 , откуда , откуда 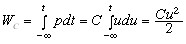
Т. к. напр. u и ток i могут совп. или не совп. по направл., то мощность p м.б. как полож., так и отриц. При p > 0 емк.эл. накапл. эн., а при p < 0 – отдает. Эн., запас-я в емк. эл. к мом.t всегда полож.
В инж. практ. рез., инд. и емк. эл-ты наз. сопр-ем, инд-тью и емкостью.
|
13 Параллельное соединение элементов в цепи переменного тока.
Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: u=u1+u2
Резисторы r=r1+r2+….
Катушка индуктивности l=l1+l2+l3…
Электрический конденсатор
1/c= 1/С+1/С2….
Параллельное соединение
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: U=U1=U2=Un;
РЕЗИСТОР: При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 1/R складывается из проводимостей каждого резистора 1/Ri).
Для двух параллельно соединенных резисторов их общее сопротивление равно:R=R1*R2/R1+R2;
ЕСЛИ сопротивление R1=R2=R3=Rn, то общее сопротивление равно R=R1/n
При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.
|
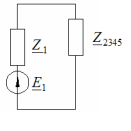
18. Баланс мощностей в цепи переменного тока.
В любой электрической цепи должен соблюдаться энергетический баланс - баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.
В левой части равенства слагаемое берется со знаком "+" если Е и I совпадают по направлению и со знаком "-" если не совпадают.
Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.
Пример: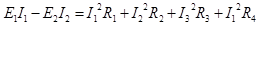
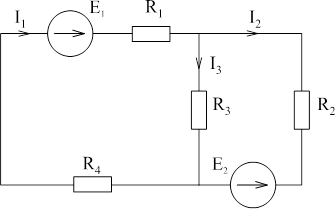
E- электро-движущая сила, I-ток, R-сопротивление
|
 10. Законы Ома и Кирхгофа в комплексной форме. 10. Законы Ома и Кирхгофа в комплексной форме.
Закон Ома: 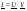
1-ый закон Кирхгофа: 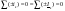
2-ой закон Кирхгофа: 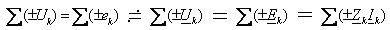
Расчет мощности по комплексному напряжению и току.
Комплексная мощность:
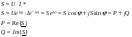
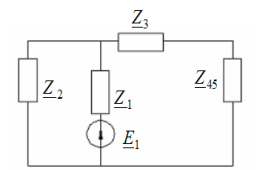
Расчет цепи с послед. соед. участков:
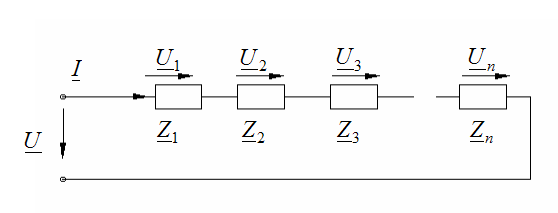
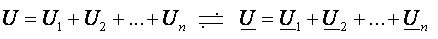
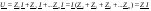 Расчет: Расчет:
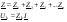 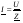
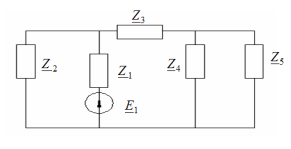
Расчет цепи с паралл.соед. участков
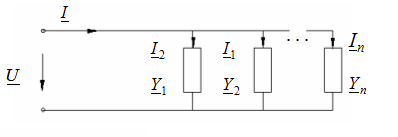
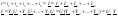
Расчет: 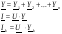 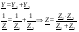 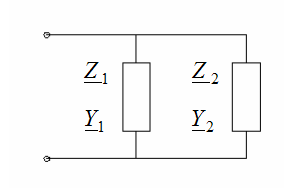
Расчет при смеш.соед. участков цепи. Смеш. соед.-это сочет. послед. и паралл. соед.
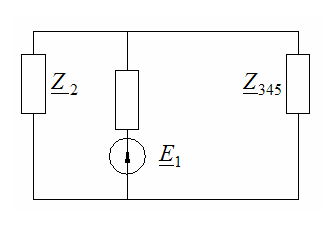
Метод «сворачивания» схемы:
Начиная с наиб. удал. от ист. цепи, происх. замена паралл. и послед. соед. 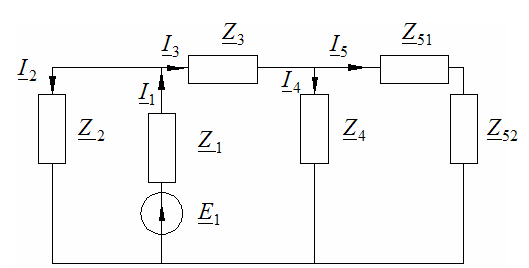
|
|
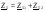
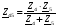
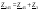
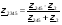
|
|
19. Способы представления симметричной трехфазной системы ЭДС формулами, векторной диаграммой, графиком.
Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного.Графики мгновенных значений трехфазной симметричной системы ЭДС показаны на рис. 3.3.Если ЭДС одной фазы (например, фазы A) принять за исходную и считать её начальную фазу равной нулю, то выражения мгновенных значений ЭДС можно записать в виде
eA=Emsinωt,
eB=Emsin(ωt−120°),
eC=Emsin(ωt−240°)=Emsin(ωt+120°).
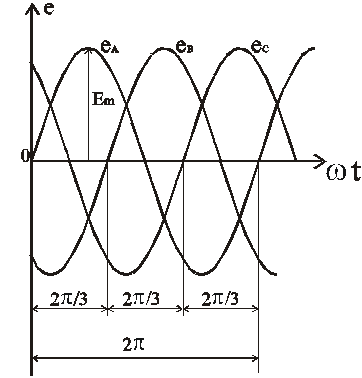
Из графика мгновенных значений (рис 3.3) следует
eA+eB+eC=0
Комплексные действующие ЭДС будут иметь выражения:
ĖA=Emej0°=Em(1+j0),
ĖB=Eme−j120°=Em(−1/2−j/2),
ĖC=Eme+j120°=Em(−1/2+j/2).
Векторная диаграмма трехфазной симметричной системы ЭДС показана на рис 3.4а.
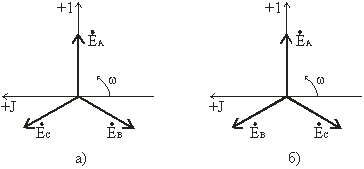
Рис. 3.4
На диаграмме рис. 3.4а вектор ĖA направлен вертикально, так как при расчете трехфазных цепей принято направлять вертикально вверх ось действительных величин. Из векторных диаграмм рис 3.4 следует, что для симметричной трехфазной системы геометрическая сумма векторов ЭДС всех фаз равна нулю:
ĖA+ĖB+ĖC=0.
|
14 вопрос - Резонанс напряжений.
Если в цепь переменного тока включены последовательно катушка индуктивности и конденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением.
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления. Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС. Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
Хобщ = XL -ХС, XL = ?L, ХС = 1 / ?С
Применив к этой цепи закон Ома, получим:
I = U / Хобщ
Формулу эту можно преобразовать следующим образом:
U = I Хобщ = I (XL -ХС) = IXL -IХС
В полученном равенстве IXL —действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХС—действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
Z=√R2(xl-xc)2;
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать: U = I / Z
Резонанс напряжений в цепи переменного тока Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем, если бы они были включены в цепь по отдельности.
Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда ?L = 1 / ?С.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R, где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = IXL так и на конденсаторе Uc = IХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений.
Следует твердо помнить, что сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ?L возрастет, а ХС = = 1 / ?С уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (XL = ХС) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.
Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.
Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.
Пружина же, сообщая маятнику в нужный момент, часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.
Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.
Итак, мы приходим к выводу, что цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему. Такая цепь получила название колебательного контура.
|
Вопрос 15
Резонанс токов. Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ?oL = 1/(?oC). Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части
цепи при резонансе I=U?(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°). Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи IL и Iс, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.
Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ?0 электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту. Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов IL и Iс. Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения
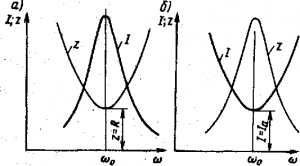 Рис. 197. Зависимость тока I и полного сопротивления Z от ? для последовательной (а) и параллельной (б) цепей переменного тока Рис. 197. Зависимость тока I и полного сопротивления Z от ? для последовательной (а) и параллельной (б) цепей переменного тока
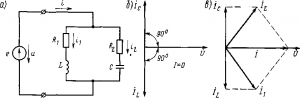 Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов
в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.
Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R1и R2, будет равенство реактивных проводимостей BL= BCветвей, в которые включены индуктивность и емкость.
Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1L и Iс равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.
Если в рассматриваемой параллельной цепи изменять частоту ?о источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.
В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ?0.
Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах. Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции
| |
|
|
 Скачать 1.24 Mb.
Скачать 1.24 Mb.