ТПС-2-609 Электротехника (...1). Практическая работа 1 Расчет параметров цепи переменного тока при резонансе напряжений. Цель работы

• Название: Практическая работа 1 Расчет параметров цепи переменного тока при резонансе напряжений. Цель работы
• Дата: 31.05.2022
• Размер: 262.34 Kb.
• Имя файла: ТПС-2-609 Электротехника (...1).docx
• Тип: Практическая работа; #559141

Задание на 23.10.

Выполните практические работы.

Выполненную работу прислать на электронную почту.
[e-mail].

ПРАКТИЧЕСКАЯ РАБОТА 1
Расчет параметров цепи переменного тока при резонансе напряжений.

Цель работы: проанализировать условия возникновения в цепи резонанса напряжений и свойства цепи при резонансе.
Содержание работы и методические рекомендации

1. 
   Вычертить заданный участок цепи.
   

Таблица 34.1

Вариант-схема	1-А 11-Б 21-В	2-А 12-Б 22-В	3-А 13-Б 23-В	4-А 14-Б 24-В	5-А 15-Б 25-В	6-А 16-Б 26-В	7-А 17-Б 27-В	8-А 18-Б 28-В	9-А 19-Б 29-В	10-А 20-Б 30-В
U, В	50	80	120	60	40	30	20	70	90	100
Ψu, °	40	-40	30	-30	20	-20	10	-40	45	0
R1, Ом	4	3	40	4	2	4	2	4	5	4
R2, Ом	3	4	20	6	3	3	2	5	4	2
R3, Ом	3	6	30	10	2	3	3	3	2	3
Rк, Ом	6	3	50	4	5	6	4	2	3	5
L1, мГн	16	38	127	9,6	12,7	31,8	25,4	12,7	25,4	12,7
L2, мГн	38	16	159	15,9	12,7	19	6,4	9,5	25,4	15,9
Lк, мГн	19,1	9,6	160	12,7	15,9	19,1	12,7	6,4	96	15,9
C1, мкФ	796	531	106	796	637	796	531	796	1061	531
C2, мкФ	531	319	53	319	1061	796	796	796	796	398
C3, мкФ	531	796	133	531	1061	319	266	266	1592	319
Участок цепи	АГ	БД	ВЖ	ГК	ДЛ	ЖМ	КН	ДК	АГ	БД

2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   

7. 
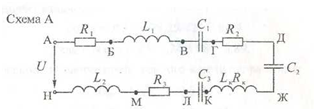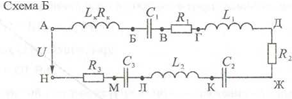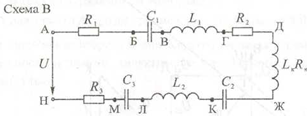   Мгновенные значения напряжения, приложенного к цепи, и тока:
   

u =√U_m·sim(ωt+ψ_u) ,

где U_m = U·√2, В; ω= 2· π·f, рад/с;

i = I_m sin (ωt+ψ_u ),

где I_m = I·√2; ψ_i= ψ_u -φ.
Для примера рассмотрим участок цепи АГ (рис. 35.1).
Поступаем аналогично: вычерчиваем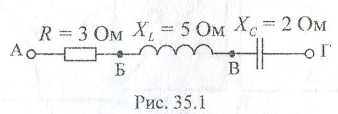







В цени протекает ток i = 2,82 sin (314·t + 13°), т.е. I_т = 2,82 А; I = 2 А; ψ_i= 13°; ω= 314 рад/с.

8. 
   Полное сопротивление участка:
   

Z_АГ= √[R²+ (X_L – Х_C)²]= √[3² + (5 – 2)²]= 4,24 Ом.

9. 
   Действующее значение напряжения, приложенного к участку цепи
   

U_АГ = I·Z_АГ = 2·4,24 = 8,48 В.

10. 
    Сдвиг фаз тока в цепи и напряжения, приложенного к заданному участку:
    

φ_аг = arctg (X_L – Х_C)/R = arctg (5 - 2)/3 = 45°,

т.е. напряжение U_АГ опережает (φ > 0) по фазе ток, протекающий в цепи на 45°. Активная мощность:

Р = U_АГ·I·cos φ_аг = 8,48·2· 0,707 = 12 Вт.

11. 
    Построить векторную диаграмму тока и напряжения с учетом начальной фазы тока ψ₁(рис. 35.2).
    

U_a = I·R = 2·3 =6 В;

Ui = I·X_L = 2·5 = 10 В;

U_c = I·Х_С = 2·2 = 4 В.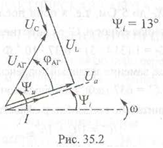

Из векторной диаграммы: U_АГ = 8,5 В; φ= 45°; ψ_и = 58°.

Сравнить значения напряжения с расчетом в п. 3 и результатом, получен­ным в предыдущей работе (п. 10),

6. 
   Записать выражение для мгновенного напряжения на заданном участке.
   

U_аг =U_m·sin (ω·t + ψ_и) = 12 sin (314·t + 58°),

где: U_m = U _аг ·√2=8,48·√2 ==12 В, ω = 314 рад/с;

ψ_и = ψ_i + φ = 13°+ 45° = 58°,

7. 
   Проанализировать, каким образом можно добиться резонанса в цепи.
   

Резонанс напряжений возникает в цепи с последовательным соединением индуктивных и емкостных сопротивлений при условии: X_L = Х_C ; ω·L = 1/ω·С.

1. 
   При заданных параметрах L и С резонанс возникает при частоте тока, равной частоте собственных незатухающих колебаний контура с L и С:
   

ω₀ = 1/√L·C = 1/√16·10^-3·1592·10^-6= 198,14 рад/с.;

f₀ = ω₀/2·π = 198,14/2·3,14 = 31,55 Гц.

Проверка: Х_L0= ω₀·L= 198,14·16·10^-3 = 3,17 Ом;

Х_C0= 1/ω₀·С= 1/198,14·1592·10^-6= 3,17 Ом;

Х_L0= Х_C0.

2. 
   При частоте f=50 Гц резонанса напряжений можно добиться изменени­ем индуктивного сопротивления катушки. В заданной схеме X_L = 5 Ом, Х_C=2 Ом.
   

Если катушку индуктивности L =16 мГн заменить на катушку с индуктив­ностью L' = 6,37 мГн, то ее сопротивление будет X_L'= 2·π·f·L'=2 Ом, что обеспе­чит равенство реактивных сопротивлений X_L' = Хс и возникновение резонанса напряжений. Того же результата (Л/ = 2 Ом) можно добиться, если к катушке с сопротивлением X_L= 5 Ом подключить параллельно катушку с сопротивлением X_LД. Из условия 1/X_LД = 1/X_L' - 1/ X_L = 1/2-1/5=3/10, т.е. X_LД=3,33 Ом. Таким со­противлением обладает катушка индуктивностью L_Д= X_LД/314= 10,6 мГн.

3. 
   При частоте f=50 Гц резонанса напряжений можно добиться, если без изменения L увеличить Хс до 5 Ом, т.е. в цепи последовательно с катушкой L должна быть результирующая емкость С' с сопротивлением Х_С' = 5 Ом
   

С' = 1/ω·Хс = 1/(314·5) = 6,37·10^-4 Ф = 637 мкФ.

Этого можно добиться, заменив заданный конденсатор емкостью С=1592 мкФ на конденсатор емкостью С=637 мкФ, либо подключив последовательно с задан­ным конденсатором дополнительно конденсатор емкостью С_Д из условия:

1/С'= 1/С + 1/С_Д;

1/637 = 1/1592+ 1/С_Д;

1/С_д= 1/637- 1/1592 = 1/1062;

С_д= 1062 мкФ.

Проверка: С' = С·С_Д/(С+ С_д) = 1592·1062/(1592 + 1062) = 637 мкФ.

8. 
   Ток в цепи при резонансе напряжений:
   

I= U_АГ/Z_АГ; Z_АГ = R = 3 Ом (т.к. X_L =Х_C);

I =8,48/3=2,83 А;

I_т = 2,83·√2 =4 А; i = 4 sin (314·t + 13°).

8. 
   Векторная диаграмма в режиме резонанса (рис. 35.3) построена для цепи с сопротивлениями R = 3 Ом; X_L = Х_C = 5 Ом. При этом напряжения на элемен­тах цепи: U_a= I·R = 2,83·3 =8,5 В; U_L= U_C = I·X= 2,83·5 = 14,15 В.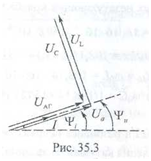
   

Из диаграммы: U= U_а = 8,5 В; φ = 0; ψ_и = ψ_i = 13°.

Мощности цепи при резонансе напряжений:

• 
  активная Р = U·I· cosφ = 8,48·2,83·1 = 24 Вт;
  

-- реактивная Q = U·I sin φ = 0 вар;

• 
  полная S = U·I = 8,48·2,83 = 24 ВА.
  

Выводы: свойства электрической цепи при резонансе напряжений.

ПРАКТИЧЕСКАЯ РАБОТА 2
Расчет параметров цепи переменного тока при резонансе токов
Цель работы: рассчитать электрическую цепь переменного тока (f = 50 Гц) с параллельным соединением активных и реактивных сопротивлений графиче­ским методом.

Содержание работы

Вычертить схему и выписать из табл. 36,1 параметры цепи согласно варианту.

Таблица 36.1

Вариант - схема	1-А 11-Б 21-В	2-А 12-Б 22-В	3-А 13-Б 23-В	4-А 14-Б 24-В	5-А 15-Б 25-В	6-А 16-Б 26-В	7-А 17-Б 27-В	8-А 18-Б 28-В	9-А 19-Б 29-В	10-А 20-Б 30-В	0-Б
U, В	20	30	40	50	60	70	60	90	100	110	70
Ψu, °	30	45	60	90	0	-90	-80	-45	-30	-30	30
R1, Ом	3	4	8	6	6	8	12	16	12	6	3
X1, Ом	4	3	6	8	8	6	16	12	16	8	4
R2, Ом	8	6	3	8	16	12	10	6	8	-	8
X2, Ом	6	8	4	6	12	16	-	8	6	20	6

Порядок выполнения работы

1. 
   Полное сопротивление каждой ветви (схема Б):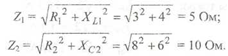
   

2. 
   Код тока в ветвях:
   

I= U/Z==7-/5=14

I= U/Z==7-/5=14

3. 
   Сдвиг фаз токов в ветвях и приложенного к цепи напряжения:
   

φ= arctg X_L1/R₁=arctg 4/3=53°

ток I₁ отстаёт по фазе от напряжения на 53°;

φ= arctg Х_C2/R₂=arctg -6/8=53°

ток I₁ опережает по фазе от напряжение на -37°;

4. 
   Векторная диаграмма напряжения и токов (рис. 36.1) строится на мил­лиметровой бумаге в масштабе, строится на мил­лиметровой бумаге в масштабе, с учетом начальной фазы напряжения.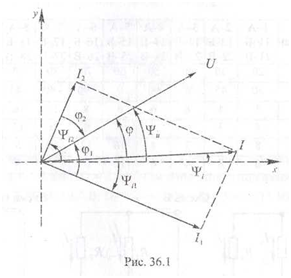
   

5. 
   Определить по векторной диаграмме:
   

- ток в неразветвлённой части цепи I= 15,7 А;

- сдвиг фаз тока I и напряжения φ= 27°;

- начальную фазу тока в неразвлетвлённой цепи ψ_i= 3°.

6. 
   Мгновенное значение напряжения и токов:
   

• 
  в общем виде и= U_m·sin (ω·t+ ψ_u),
  

где: U_m = U·√2 = 70·√2 = 99 В; ω = 2· π·f= 314

• 
  в данном случае и= 99·sin (314·t + 30°),
  
• 
  амплитуды токов:
  

I_1m = I₁·√2 =19,8 А

I_2m = I₂·√2 =9,9 А

I_m = I·√2 =22,2 А

• 
  начальные фазы токов:
  

ψ_i1= ψ_u- φ₁=30- 53=-23°

ψ_i2=ψ_u- φ₂=30-(-37)=67°

ψ_i=ψ_u- φ=30-27=3°

• 
  формулы мгновенных значений токов в цепи:
  

i₁=19,8·sin (314·t-23°),

i₂=9,9·sin (314·t+67°),

i₁=22,2·sin (314·t+3°).

7. 
   Определить
   

- активная P=U·I·cos φ=70·15,7 ·cos 27°)=979,9 Вт,

- реактивная Q=U·I ·sin φ=70·15,7 ·sin 27°)=498,9 вар,

- полная S=U·I=70·15=1099 ВА.

Выводы: применение первого закона Кирхгофа в разветвленных цепях пе­ременного тока; достоинства и недостатки графического метода расчета цепи.