Реферат Кулаковский. Последовательный и параллейный резонанс в электрических цепях
 Скачать 99.03 Kb.
|
|
Последовательный и параллейный резонанс в электрических цепях Содержание Введение……………………………………………………………....3. Понятие резонанса в электрических цепях………………………....4. Резонанс в цепи с последовательно соединенными элементами….7. Параллельный колебательный контур и резонанс токов…………..10. Заключение…………………………………………………………….12. Список используемой литературы………………………………...…13. Введение Явление резонанса можно наблюдать в любых колебательных системах, в том числе механических и электрических. Электрический резонанс возникает при определенных условиях в электрических цепях переменного тока, содержащих индуктивности и емкости. Задачи реферата: рассмотреть явление резонанса в электрической цепи; охарактеризовать последовательный и параллейный резонанс в электрических цепях. Понятие резонанса в электрических цепях Под резонансом в электрической цепи понимают такое ее состояние, когда ток и напряжение совпадают по фазе и вся цепь ведет себя как чисто активная (рис. 1.18). 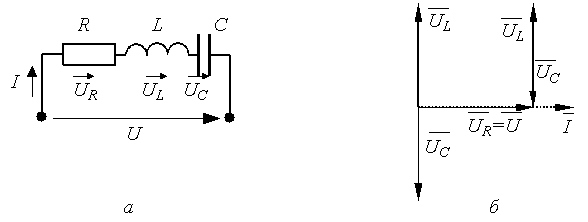 Рис. 1.18. Резонансная цепь (а) и векторная диаграмма при резонансе (б) 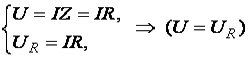 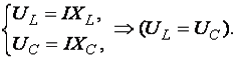(из определения резонанса); (условие резонанса напряжений);  ; ; Если 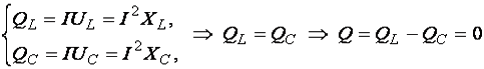 то  , т.е. напряжение на реактивных элементах цепи может быть больше напряжения, подводимого ко всей цепи. , ,т.е. цепь из сети реактивную мощность не потребляет и в сеть её не отдает;  ; .В момент резонанса происходит обмен энергии между L и C. Из сети реактивная мощность не потребляется и в сеть не отдается, следовательно, цепь ведет себя как чисто активная. Резонанс токов возникает при параллельном соединении реактивных сопротивлений с одинаковыми характеристиками в цепях с переменным током. Во время резонанса токов реактивная индуктивная проводимость приравнивается к реактивной емкостной проводимости, то есть \(BL=BC.\) Колебания контура с определенной частотой совпадают с частотой колебаний источника. Простейшим примером цепи, в которой может произойти резонанс токов, есть параллельное соединение катушки с конденсатором. Поскольку реактивные сопротивления совпадают по модулю, то амплитуды токов конденсатора и катушки также будут совпадать и могут достичь наибольшего значения амплитуды. Согласно первому закону Кирхгофа \(IR\) равняется току источника. Иначе говоря, ток проходит лишь через резистор. Если рассмотреть параллельный контур \(LC,\) то при частоте резонанса его сопротивление будет огромным. В условиях режима гармонии при частоте резонанса в контуре будет расход тока лишь для восполнения потерь на активном сопротивлении. Значит, в последовательной цепи \(RLC\) импеданс наименьший при частоте резонанса и равняется активному сопротивлению контура, при этом в параллельной цепи \(RLC\) импеданс наибольший при частоте резонанса и равняется сопротивлению утечки, что фактически есть активным сопротивлением контура. Это значит, что для обеспечения резонанса силы тока или напряжения в цепи необходима ее проверка с целью определения суммарного сопротивления и проводимости. Кроме того, ее мнимая часть должна равняться нулю. Резонанс напряжений имеет место в цепи переменного тока в случае последовательного соединения активного \(R\) , емкостного \(C\) и индуктивного \(L\) компонентов. Резонанс напряжений состоит в совпадении внутренних колебаний источника и внешних колебаний контура. Резонанс напряжений применяется с пользой, но бывает и опасен. Например, данное явление применяют в радиотехнике, а опасность его состоит в том, что при резких скачках напряжения может произойти поломка оборудования и даже его возгорание. Резонанс напряжения достигают несколькими путями: подбирая индуктивность катушки; подбирая емкость конденсатора; подбирая угловую частоту \(ω_0\) . Эти величины подбирают с помощью таких формул: Частота \(ω_0\) – это резонансная величина. При постоянных напряжении и активном сопротивлении в цепи сила тока в процессе резонанса напряжения наибольшая и равняется отношению напряжения к активному сопротивлению. То есть, сила тока полностью не зависима от реактивного сопротивления. Если реактивные сопротивления индукции и емкости одинаковы и по своей величине превышают активное сопротивление, тогда на зажимах катушки и конденсатора будет напряжение, сильно превышающее напряжение на зажимах контура. Не нашли что искали? Просто напиши и мы поможем Кратность превышения напряжения на зажимах катушки и конденсатора в соотношении с напряжением контура рассчитывается так: Величина \(Q\) является добротностью контура и описывает его резонансные характеристики. Величина, обратная добротности контура, – это затухание контура \( <1 \over Q>\) . Явление резонанса на практике Электрический резонансный трансформатор, который был разработан Николой Теслой в конце XIX века, является ярким примером практического применения резонанса в электрических цепях. Тесла проводил массу экспериментов при разных конфигурациях резонансных цепей. На сегодняшний день словосочетанием «катушка Теслы» называют высоковольтные резонансные трансформаторы. Такие приспособления применяют для генерации высокого напряжения и частоты переменного тока. Если простые трансформаторы используют для передачи энергии с первичной на вторичную катушку, то резонансные — для хранения электрической энергии во временном режиме. При помощи данного приспособления, посредством управления воздушным сердечником резонансно настроенного трансформатора, при незначительной силе тока получают высокие напряжения. При этом у каждой катушки есть собственная емкость и она работает как резонансный контур. Для создания еще большего напряжения достигают резонанса двух контуров. Резонанс в цепи с последовательно соединенными элементами Резонанс напряжений 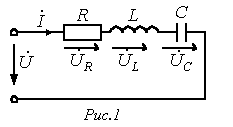 Для цепи на рис.1 имеет место 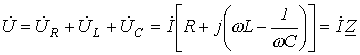 где
В зависимости от соотношения величин  и  возможны три различных случая.1. В цепи преобладает индуктивность, т.е. 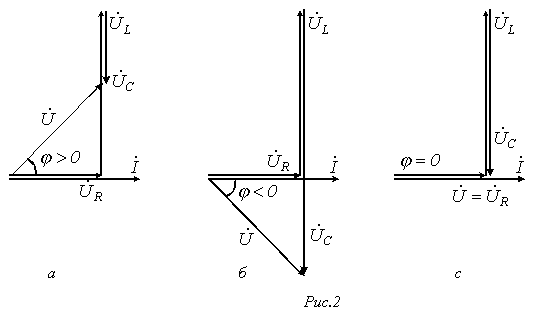 , а следовательно, . Этому режиму соответствует векторная диаграмма на рис. 2,а. 2.В цепи преобладает емкость, т.е.  , а значит,  . Этот случай отражает векторная диаграмма на рис. 2,б.3.  - случай резонанса напряжений (рис. 2,в).Условие резонанса напряжений
При этом, как следует из (1) и (2),  .При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания. Пусть, например, в цепи на рис. 1    . Тогда  , и, соответственно,  .Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков. Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной. Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных элементов. Действительно, в этом случае 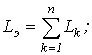 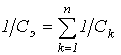 , и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ .Как показывает анализ уравнения (3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (3) для резонансной частоты можно записать
Параллельный колебательный контур и резонанс токов Явление резонанса токов удобно изучать применительно к электрической цепи с параллельно соединенными r, L и С (рис. 5-6), так как при этом можно непосредственно воспользоваться результатами, полученными в предыдущем параграфе. Действительно, выражение для комплексной проводимости такой цепи 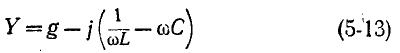 по своей структуре аналогично выражению (5-1), причем резонансная частота определяется согласно (5-2). Добротность резонансной цепи на основании (5-3) 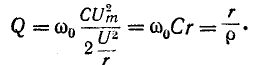 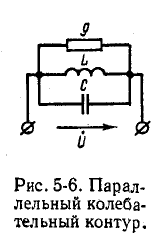 По аналогии с предыдущим выражение (5-13) приводится к виду: Сравнивая полученный результат с (5-6), убеждаемся в том, что выражение Y/g для схемы рис. 5-6 имеет тот же вид, что и выражение  для схемы рис. 5-1.Поэтому кривые рис. 5-2 применимы и в данном случае: кривые рис. 5-2, а выражают зависимость от 6 Отношения y/g, а кривые рис. 5-2, б — зависимость угла —  Кривые рис. 5-2, а показывают, что при резонансе токов полная проводимость цепи минимальна, т. е. входное сопротивление достигает максимума. При заданном напряжении 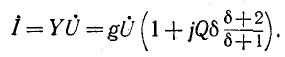 на выводах цепи ток, идущий от источника в цепь, равен: Этот ток достигает минимума при резонансной частоте, так как при этом  Следовательно, отношение. токов 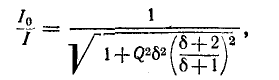 определяется из выражения правая часть которого полностью совпадает с (5-8). В связи с этим резонансные кривые рис. 5-3 выражают применительно к схеме рис. 5-6 зависимость  В случае резонанса токов токи в индуктивном и емкостном элементах схемы рис. 5-6 равны и противоположны по знаку:  Полученное выражение показывает, что добротность рассматриваемой цепи определяется как кратность токов в L и С по отношению к суммарному току  При Q > 1 эти токи превышают Если параллельный колебательный контур питается от источника тока с внутренним сопротивлением  то чем меньше сопротивление присоединяемое параллельно сопротивлению r, тем ниже добротность и шире полоса пропускания контура. Поэтому в отличие от последовательного колебательного контура с точки зрения сокращения. полосы пропускания параллельного колебательного контура выгоден источник тока с большим внутренним сопротивлением.Заключение Изучение электрического резонанса необходимо, так как это явление широко используется в технике электросвязи, а в установках сильного тока, где его возникновение специально не предусматривается, резонанс может оказаться опасным (могут возникнуть перенапряжения и пробой изоляции). Список используемой литературы Александров, Ю.Г.; Панарин, С.А. Деревня Востока: от социальной напряженности к политической борьбе (аграрные социальные конфликты 70 -- 80 -х годов); Наука - М., 2021. - 288 c. Любимов, К.В.; Новиков, С.М. Знакомимся с электрическими цепями; Наука - М., 2020. - 112 c. Фираго, Б.И.; Павлячик, Л.Б. Регулируемые электроприводы переменного тока; Техноперспектива - М., 2020. - 363 c. |
;
.
.
.
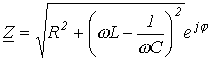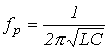