Контрольная-работа-вариант-2. 1 На рисунке справа схема дорог нского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах)
 Скачать 376.13 Kb. Скачать 376.13 Kb.
|
|
№1-1. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). 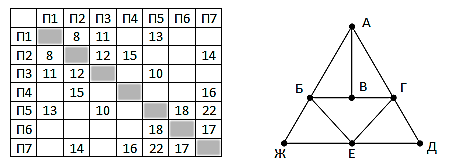 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина кратчайшего пути из пункта A в пункт Ж превышает 30 километров. Определите длину кратчайшего пути между пунктами В и Е. №1-2. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). 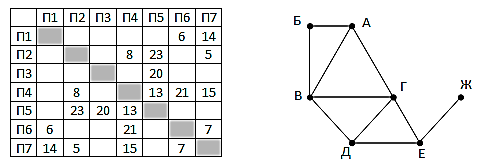 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Укажите кратчайший путь из пункта Б в пункт Ж. В ответе перечислите все населённые пункты, через которые проходит путь. Например, путь из Г в В через А и Б записывается как ГАБВ. №2-1. В фрагменте базы данных представлены сведения о родственных отношениях. Определите ID человека, у которого в момент рождения была самая молодая бабушка. 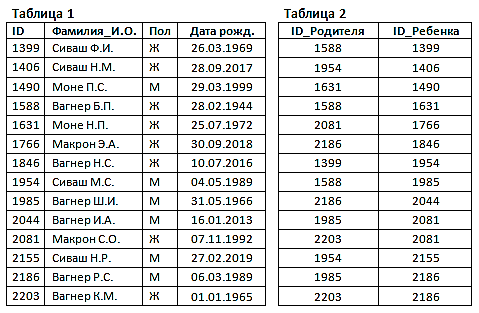 №2-2. В фрагменте базы данных представлены сведения о родственных отношениях. Определите максимальную разницу между годами рождения двух родных сестер. 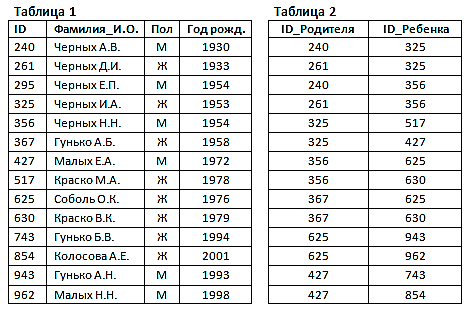 №3-1. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я . Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 11, Б – 101, Я – 010. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ГРАММ? №3-2. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0, для буквы Б – кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов? №4-1. Все 5-буквенные слова, составленные из букв А, З, Н, С, записаны в алфавитном порядке и пронумерованы. Вот начало списка: 1. ААААА 2. ААААЗ 3. ААААН 4. ААААС 5. АААЗА ... Какое количество слов находятся между словами САЗАН и ЗАНАС (включая эти слова)? №4-2. Все 4-буквенные слова, составленные из букв К, Л, Р, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка: 1. КККК 2. КККЛ 3. КККР 4. КККТ ... На каком месте от начала списка стоит слово ТТЛК №4-3. Андрей составляет 7-буквенные коды из букв А, Н, Д, Р, Е, Й. Буквы А и Й должны встречаться в коде ровно по одному разу, при этом буква Й не может стоять на первом месте. Остальные допустимые буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Андрей? №5-1. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Л и проходящих через город Ж, но НЕ проходящих через город З? 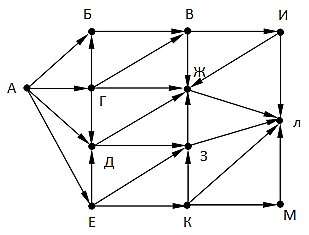 №5-2. На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город Г? 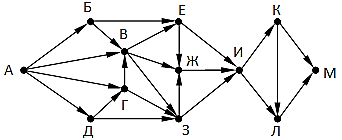 №6-1. Значение выражения (51278 - 51260)∙(5125 + 645) записали в системе счисления с основанием 8. Сколько цифр 7 содержится в этой записи? №6-2. Сколько значащих нулей в двоичной записи числа 4812 + 8800 - 23125 - 865 - 4312 + 130 №7. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 61. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 61 или больше камней. В начальный момент в первой куче было 10 камней, во второй куче – S камней, 1 ≤ S ≤ 50. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Ответьте на следующие вопросы: Вопрос 1. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно. Вопрос 2. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания. Вопрос 3. Сколько существует значений S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. |
