проект нейросети. 1 Нейронные компьютерные системы понятие, модели, история развития
 Скачать 207.58 Kb. Скачать 207.58 Kb.
|
|
Содержание Введение………………………………………………………………….. 1 Нейронные компьютерные системы: понятие, модели, история развития………………………………………………………………………… 1.1 Понятие нейронных систем. История развития нейронных систем…………………………………………………………………………… 1.2 Модели нейронных компьютерных систем………………………. 2 Анализ развития и внедрения нейронных компьютерных систем в современном обществе…………………………………………………………. 2.1 Способы реализации нейронных сетей ……………………………. 2.2 Внедрение нейронных компьютеров и их влияние на кибернетизацию общества……………………………………………………… 3 Внедрение нейронных систем в России как определяющий фактор развития государства……………………………………………………………… 3.1 Внедрение нейронных систем в России на современном этапе развития государства……………………………………………………………. 3.2Проблемы и перспективы внедрения нейронных систем……………………………………………………………………………… Заключение Список используемой литературы 1 Нейронные компьютерные системы: понятие, модели, история развития 1.1 Понятие нейронных систем. История развития нейронных систем Нейрокомпьютинг - это научное направление, занимающееся разработкой вычислительных систем шестого поколения - нейрокомпьютеров, которые состоят из большого числа параллельно работающих простых вычислительных элементов (нейронов)1. Элементы связаны между собой, образуя нейронную сеть. Они выполняют единообразные вычислительные действия и не требуют внешнего управления. Большое число параллельно работающих вычислительных элементов обеспечивают высокое быстродействие. В настоящее время разработка нейрокомпьютеров ведется в большинстве промышленно развитых стран. Нейрокомпьютеры позволяют с высокой эффективностью решать целый ряд интеллектуальных задач. Это задачи распознавания образов, адаптивного управления, прогнозирования, диагностики и так далее. Нейрокомпьютеры отличаются от электронных вычислительных машин предыдущих поколений не просто большими возможностями. Принципиально меняется способ использования машины. Место программирования занимает обучение, нейрокомпьютер «учится» решать задачи. Обучение - корректировка весов связей, в результате которой каждое входное воздействие приводит к формированию соответствующего выходного сигнала2. После обучения сеть может применять полученные навыки к новым входным сигналам. При переходе от программирования к обучению повышается эффективность решения интеллектуальных задач. Вычисления в нейронных сетях существенно отличаются от традиционных, в силу высокойпараллеленности их можно рассматривать как коллективное явление. В нейронной сети нет локальных областей, в которых запоминается конкретная информация. Вся информация запоминается во всей сети. Толчком к развитию нейрокомпьютинга послужили биологические исследования. По данным нейробиологии нервная система человека и животных состоит из отдельных клеток - нейронов. (рис. 1) В мозге человека их число достигает 1.0e10 - 1.0e12.3 Каждый нейрон связан с 1.0e3 - 1.0e4 другими нейронами и выполняет сравнительно простые действия. Время срабатывания нейрона - 2-5 мс4. Совокупная работа всех нейронов обуславливает сложную работу мозга, который в реальном времени решает сложнейшие задачи. 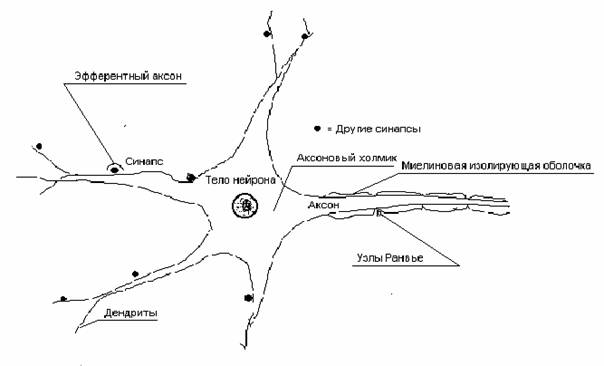 Рисунок 1.- Схема биологического нейрона Отличия нейрокомпьютеров от вычислительных устройств предыдущих поколений: параллельная работа очень большого числа простых вычислительных устройств обеспечивает огромное быстродействие; нейронная сеть способна к обучению, которое осуществляется путем настройки параметров сети; высокая помехо- и отказоустойчивость нейронных сетей; простое строение отдельных нейронов позволяет использовать новые физические принципы обработки информации для аппаратных реализаций нейронных сетей. Нейронные сети находят свое применение в системах распознавания образов, обработки сигналов, предсказания и диагностики, в робототехнических и бортовых системах. Нейронные сети обеспечивают решение сложных задач за времена порядка времен срабатывания цепочек электронных и/или оптических элементов. Решение слабо зависит от неисправности отдельного нейрона. Это делает их привлекательными для использования в бортовых интеллектуальных системах5. Разработки в области нейрокомпьютеров поддерживаются целым рядом международных и национальных программ. В настоящее время эксплуатируется не менее 50 нейросистем в самых различных областях - от финансовых прогнозов до экспертизы6. Разработки в области нейрокомпьютинга ведутся по следующим направлениям: разработка нейроалгоритмов; создание специализированного программного обеспечения для моделирования нейронных сетей; разработка специализированных процессорных плат для имитации нейросетей; электронные реализации нейронных сетей; оптоэлектронные реализации нейронных сетей. В настоящее время наиболее массовым направлением нейрокомпьютинга является моделирование нейронных сетей на обычных компьютерах, прежде всего персональных. Моделирование сетей выполняется для их научного исследования, для решения практических задач, а также при определении значений параметров электронных и оптоэлектронных нейрокомпьютеров. В основу искусственных нейронных сетей положены следующие черты живых нейронных сетей, позволяющие им хорошо справляться с нерегулярными задачами: простой обрабатывающий элемент - нейрон; очень большое число нейронов участвует в обработке информации; один нейрон связан с большим числом других нейронов (глобальные связи); изменяющиеся веса связей между нейронами; массированная параллельность обработки информации. Прототипом для создания нейрона послужил биологический нейрон головного мозга. Биологический нейрон имеет тело, совокупность отростков - дендридов, по которым в нейрон поступают входные сигналы, и отросток - аксон, передающий выходной сигнал нейрона другим клеткам. Точка соединения дендрида и аксона называется синапсом7. Упрощенно функционирование нейрона можно представить следующим образом: нейрон получает от дендридов набор (вектор) входных сигналов; в теле нейрона оценивается суммарное значение входных сигналов. Однако входы нейрона неравнозначны. Каждый вход характеризуется некоторым весовым коэффициентом, определяющим важность поступающей по нему информации. Таким образом, нейрон не просто суммирует значения входных сигналов, а вычисляет скалярное произведение вектора входных сигналов и вектора весовых коэффициентов; нейрон формирует выходной сигнал, интенсивность которого зависит от значения вычисленного скалярного произведения. Если оно не превышает некоторого заданного порога, то выходной сигнал не формируется вовсе - нейрон «не срабатывает»; выходной сигнал поступает на аксон и передается дендридам других нейронов. Поведение искусственной нейронной сети зависит как от значения весовых параметров, так и от функции возбуждения нейронов.(рис. 2) Известны три основных вида функции возбуждения: пороговая, линейная и сигмоидальная. Для пороговых элементов выход устанавливается на одном из двух уровней в зависимости от того, больше или меньше суммарный сигнал на входе нейрона некоторого порогового значения. Для линейных элементов выходная активность пропорциональна суммарному взвешенному входу нейрона. 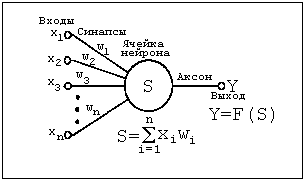 Рисунок 2. - Искусственный нейрон Для сигмоидальных элементов в зависимости от входного сигнала, выход варьируется непрерывно, но не линейно, по мере изменения входа. Сигмоидальные элементы имеют больше сходства с реальными нейронами, чем линейные или пороговые, но любой из этих типов можно рассматривать лишь как приближение. Нейронная сеть представляет собой совокупность большого числа сравнительно простых элементов - нейронов, топология соединений которых зависит от типа сети. Чтобы создать нейронную сеть для решения какой-либо конкретной задачи, мы должны выбрать, каким образом следует соединять нейроны друг с другом, и соответствующим образом подобрать значения весовых параметров на этих связях. Может ли влиять один элемент на другой, зависит от установленных соединений. Вес соединения определяет силу влияния. 1.2 Модели нейронных компьютерных систем На сегодняшнем этапе развития нейросистем выделяют 4 основных модели: Модель Маккалоха Модель Розенблата Модель Хопфилда Модель сети с обратным распространением Теоретические основы нейроматематики были заложены в начале 40-х годов. В 1943 году У. Маккалох и его ученик У. Питтс сформулировали основные положения теории деятельности головного мозга8. Ими были получены следующие результаты: разработана модель нейрона как простейшего процессорного элемента, выполняющего вычисление переходной функции от скалярного произведения вектора входных сигналов и вектора весовых коэффициентов; предложена конструкция сети таких элементов для выполнения логических и арифметических операций; сделано основополагающее предположение о том, что такая сеть способна обучаться, распознавать образы, обобщать полученную информацию. Несмотря на то, что за прошедшие годы нейроматематика ушла далеко вперед, многие утверждения Макклоха остаются актуальными и поныне. В частности, при большом разнообразии моделей нейронов принцип их действия, заложенный Макклохом и Питтсом, остается неизменным. Недостатком данной модели является сама модель нейрона «пороговой» вид переходной функции.(рис. 3) В формализме У. Маккалоха и У. Питтса нейроны имеют состояния 0, 1 и пороговую логику перехода из состояния в состояние9. Каждый нейрон в сети определяет взвешенную сумму состояний всех других нейронов и сравнивает ее с порогом, чтобы определить свое собственное состояние. 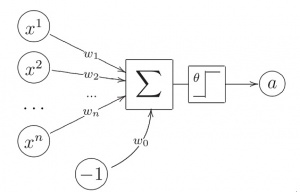 Рисунок 3. – Модель Маккалоха Пороговый вид функции не предоставляет нейронной сети достаточную гибкость при обучении и настройке на заданную задачу. Если значение вычисленного скалярного произведения, даже незначительно, не достигает до заданного порога, то выходной сигнал не формируется вовсе и нейрон «не срабатывает». Это значит, что теряется интенсивность выходного сигнала (аксона) данного нейрона и, следовательно, формируется невысокое значение уровня на взвешенных входах в следующем слое нейронов. Серьезное развитие нейрокибернетика получила в работах американского нейрофизиолога Френсиса Розенблата (Корнелльскийуниверситет)10. В 1958 году он предложил свою модель нейронной сети.(рис. 4) Розенблат ввел в модель Маккаллока и Питтса способность связей к модификации, что сделало ее обучаемой. Эта модель была названа перцептроном. Первоначально перцептрон представлял собой однослойную структуру с жесткой пороговой функцией процессорного элемента и бинарными или многозначными входами. Первые перцептроны были способны распознавать некоторые буквы латинского алфавита. Впоследствии модель перцептрона была значительно усовершенствована. 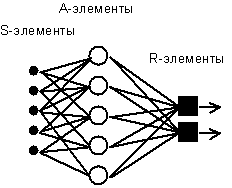 Рисунок 4. – Модель перцептронаРозенблата Перцептрон применялся для задачи автоматической классификации, которая в общем случае состоит в разделении пространства признаков между заданным количеством классов. В двухмерном случае требуется провести линию на плоскости, отделяющую одну область от другой. Перцептронспособен делить пространство только прямыми линиями (плоскостями). Алгоритм обучения перцептрона выглядит следующим образом: системе предъявляется эталонный образ; если выходы системы срабатывают правильно, весовые коэффициенты связей не изменяются; если выходы срабатывают неправильно, весовым коэффициентам дается небольшое приращение в сторону повышения качества распознавания. Серьезным недостатком перцептрона является то, что не всегда существует такая комбинация весовых коэффициентов, при которой имеющееся множество образов будет распознаваться данным перцептроном. Причина этого недостатка состоит в том, что лишь небольшое количество задач предполагает, что линия, разделяющая эталоны, будет прямой. Обычно это достаточно сложная кривая, замкнутая или разомкнутая. Если учесть, что однослойный перцептрон реализует только линейную разделяющую поверхность, применение его там, где требуется нелинейная, приводит к неверному распознаванию (эта проблема называется линейной неразделимостью пространства признаков). Выходом из этого положения является использование многослойного перцептрона, способного строить ломаную границу между распознаваемыми образами. Описанная проблема не является единственной трудностью, возникающей при работе с перцептронами - также слабо формализовани метод обучения перцептрона. Перцептрон поставил ряд вопросов, работа над решением которых привела к созданию более «разумных» нейронных сетей и разработке методов, нашедших применение не только в нейрокибернетике (например, метод группового учета аргументов, применяемый для идентификации математических моделей). В 70-е годы интерес к нейронным сетям значительно упал, однако работы по их исследованию продолжались. Был предложен ряд интересных разработок, таких, например, как когнитрон), позволяющих распознавать образы независимо от поворота и изменения масштаба изображения11. Автором когнитрона является японский ученый И. Фукушима. Новый виток быстрого развития моделей нейронных сетей, который начался лет 15 тому назад, связан с работами Амари, Андерсона, Карпентера, Кохонена и других, и в особенности, Хопфилда, а также под влиянием обещающих успехов оптических технологий и зрелой фазы развития СБИС для реализации новых архитектур12. Начало современному математическому моделированию нейронных вычислений было положено работами Хопфилда в 1982 году, в которых была сформулирована математическая модель ассоциативной памяти на нейронной сети. Показано, что для однослойной нейронной сети со связями типа «все на всех» характерна сходимость к одной из конечного множества равновесных точек, которые являются локальными минимумами функции энергии, содержащей в себе всю структуру взаимосвязей в сети. Понимание такой динамики в нейронной сети было и у других исследователей.(рис.5) Однако,Хопфилд и Тэнк показали как конструировать функцию энергии для конкретной оптимизационной задачи и как использовать ее для отображения задачи в нейронную сеть. Этот подход получил развитие и для решения других комбинаторных оптимизационных задач. Привлекательность подхода Хопфилда состоит в том, что нейронная сеть для конкретной задачи может быть запрограммирована без обучающих итераций. Веса связей вычисляются на основании вида функции энергии, сконструированной для этой задачи. 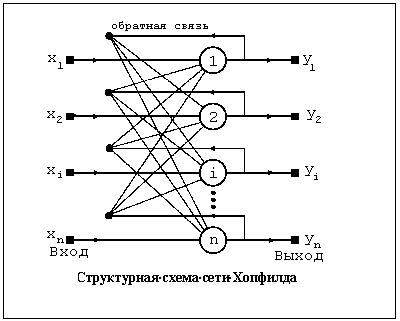 Рисунок 5. – Структурная модель сети Хопфилда Развитием модели Хопфилда для решения комбинаторных оптимизационных задач и задач искусственного интеллекта является машина Больцмана, предложенная и исследованная Джефери Е. Хинтоном и Р. Земелом. В ней, как и в других моделях, нейрон имеет состояния 1, 0 и связь между нейронами обладает весом. Каждое состояние сети характеризуется определенным значением функции консенсуса (аналог функции энергии). Максимум функции консенсуса соответствует оптимальному решению задачи. Способом обратного распространения (backpropogation) называется способ обучения многослойных нейронных сетей (НС). (рис.6) 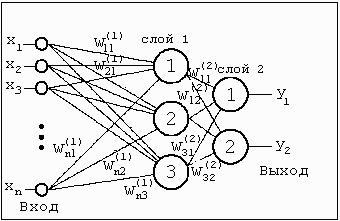 Рисунок 6. - Многослойная нейронная сеть В таких НС связи между собой имеют только соседние слои, при этом каждый нейрон предыдущего слоя связан со всеми нейронами последующего слоя. Нейроны обычно имеют сигмоидальную функцию возбуждения. Первый слой нейронов называется входным и содержит число нейронов соответствующее распознаваемому образу. Последний слой нейронов называется выходным и содержит столько нейронов, сколько классов образов распознается. Между входным и выходным слоями располагается один или более скрытых (теневых) слоев. Определение числа скрытых слоев и числа нейронов в каждом слое для конкретной задачи является неформальной задачей. Принцип обучения такой нейронной сети базируется на вычислении отклонений значений сигналов на выходных процессорных элементах от эталонных и обратном «прогоне» этих отклонений до породивших их элементов с целью коррекции ошибки. Еще в 1974 году Поль Дж. Вербос изобрел значительно более эффективную процедуру для вычисления величины, называемой производной ошибки по весу, когда работал над своей докторской диссертацией в Гарвардском университете13. Процедура, известная теперь как алгоритм обратного распространения, стала одним из наиболее важных инструментов в обучении нейронных сетей. Однако этому алгоритму свойственны и недостатки, главный из которых - отсутствие сколько-нибудь приемлемых оценок времени обучения. Понимание, что сеть в конце концов обучится, мало утешает, если на это могут уйти годы. Тем не менее, алгоритм обратного распространения имеет широчайшее применение. |
