Иррациональная функция. 1 Область определения функции. Точки разрыва функции. 2 Четность или нечетность функции

• Название: 1 Область определения функции. Точки разрыва функции. 2 Четность или нечетность функции
• Дата: 18.01.2022
• Размер: 92.01 Kb.
• Имя файла: Иррациональная функция.docx
• Тип: Документы; #334825

1) Область определения функции. Точки разрыва функции.
2) Четность или нечетность функции.
y(-x)=-x·(-x-1)^2/3
Функция общего вида
3) Периодичность функции.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y
x=0, y=0
Пересечение с осью 0X
y=0
x·(x-1)^2/3=0
x₁=0
5) Исследование на экстремум.
y = x*(x-1)^(2/3)
1. Находим интервалы возрастания и убывания. Первая производная.

или

Находим нули функции. Для этого приравниваем производную к нулю
5·x-3 = 0
Откуда:
x₁ = 3/5

(0 ;3/5)	(3/5; +∞)

2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

или

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Откуда точки перегиба:
x₁ = 6/5

(-∞ ;1.0)	(1.0; 6/5)	(6/5; +∞)
f''(x) > 0	f''(x) < 0	f''(x) > 0
функция вогнута	функция выпукла	функция вогнута

6) Асимптоты кривой.
y = x·(x-1)^2/3
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:


Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.
y = x·(x-1)^2/3
Найдем наклонную асимптоту при x → -∞:

Находим коэффициент k:


Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.

Рисунок №1 - График функции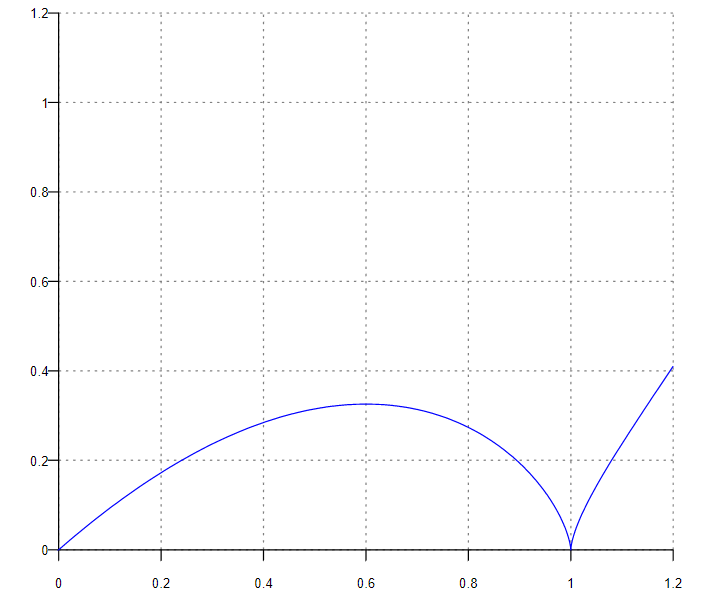



Рисунок №2 - Схематичное построение графика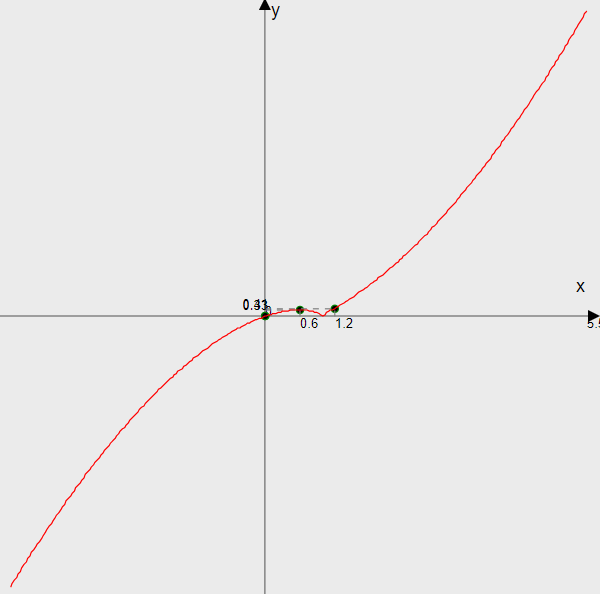