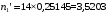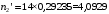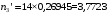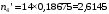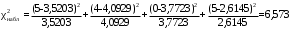|
|
Растровый электронный микроскоп. КР Растовый Электронный микроскоп. 1. Описание физических эффектов (явлений), лежащих в основе измерительного преобразования
СОДЕРЖАНИЕ
Введение. 4
1. Описание физических эффектов (явлений), лежащих в основе измерительного преобразования. 6
2. Анализ принципа работы и особенности конструкции растрового электронного микроскопа 10
3. Идентификация функции распределения результатов измерений критерием согласия Пирсона 15
Заключение 21
Список используемой литературы 23
Приложение 25
Введение
Растровая электронная микроскопия (РЭМ), является одним из наиболее распространенных методов фундаментальных и прикладных исследований в различных областях науки и техники: от нанотехнологий (исследования химического состава и анализа морфологии и структуры наноматериалов) и материаловедения до биологии и физики полупроводников 1.
Растровый электронный микроскоп (РЭМ) - электронный микроскоп, формирующий изображение объекта при сканировании его поверхности электронным зондом 2. По своим техническим возможностям он сочетает в себе качества как светового (СМ), так и просвечивающего электронного (ПЭМ) микроскопов, но является более многофункциональным 3.
Метод растровой электронной микроскопии позволяет:
Непосредственно исследовать большие площади поверхностей на массивных образцах в широком диапазоне увеличений от 10х до 50000 и выше с достаточно высоким разрешением
Исследовать общий характер структуры всей поверхности объекта при малых увеличениях и детально изучить любой участок при больших увеличениях
Наблюдать объемное изображение структуры с возможностью ее количественной оценки;
Получать полную информацию о поверхности изделия с помощью микроанализаторами химического состава, входящих в состав растрового электронного микроскопа.
Растровый электронный микроскоп обладает многообразием механизмов образования контраста, а также чрезвычайно большой глубиной резкости изображения и высоким пространственным разрешением.
Высокая разрешающая способность РЭМ широко применяется для металлографического исследования дисперсных элементов структуры материала, оценки морфологии частиц порошков, сильно отличающихся по размерам, например, с радиусом частиц 0,05 мкм и 1 мм, дисперсию и другие параметры, требующие получение объемной информации.
Выпускаемые приборы РЭМ имеют увеличение от десятков до нескольких сотен тысяч раз. Растровые электронные микроскопы имеют в 103 раз большую величину глубины резкости по сравнению с оптическими приборами (например, при увеличении ×500 глубина резкости составляет 0,5 мм). Это обеспечивает значительно более высокое качество изображения при сравнимых увеличениях и позволяет успешно применять методику получения стереопар.
Данная курсовая работа имеет своей целью изучение использования растровой электронной микроскопии в нанометровом и микрометровом масштабе.
Для выполнения цели курсовой работы были поставлены следующие задачи:
изучение физических основ растровой электронной микроскопии.
анализ принципа работы основных блоков растрового электронного микроскопа, особенности конструкции растрового электронного микроскопа
идентификация функции распределения результатов измерения, полученных в результате измерений растровым электронным микроскопом.
Выбранная тема курсовой работы является актуальной на сегодняшний день, т.к. высокая информативность, простота изготовления объектов для исследования, высокая степень автоматизации количественного анализа изображения и обработки результатов измерений, высокое пространственное разрешение, достигающее 1 нм, возможность оснащения микроскопа различными детекторами сигналов, значительно расширяющих диапазон получаемых данных и др. делают РЭМ наиболее универсальным прибором для исследования и получения данных о размерах, форме, структуры и других физико-химических свойствах гетерогенных органических и неорганических материалов в наноинженерии. Вышеперечисленные преимущества РЭМ определяют методические особенности использования РЭМ и создают целый ряд новых дополнительных аналитических возможностей в области электронной микроскопии 5.
ОПИСАНИЕ ФИЗИЧЕСКИХ ЭФФЕКТОВ (ЯВЛЕНИЙ), ЛЕЖАЩИХ В ОСНОВЕ ИЗМЕРИТЕЛЬНОГО ПРЕОБРАЗОВАНИЯ
Принцип действия растровой микроскопии основан на использовании эффектов, возникающих при облучении поверхности объектов тонко сфокусированным пучком электронов – зондом. Сигналами для получения изображения в РЭМ служат вторичные, отраженные и поглощённые электроны. Остальные излучения применяются в РЭМ как дополнительные источники информации. Например, для получения информации о химическом составе материала исследуемого образца используются специальные эффекты, в частности рентгеновское излучение. 6
Как показано на рисунке 1 в результате взаимодействия первичных электронов 1 с образцом (веществом) 2 генерируются различные сигналы. Основными из них являются поток электронов: отраженных 3, вторичных 4, Оже-электронов 5, поглощенных 6, прошедших через образец 7, а также излучений: катодолюминесцентного 8 и рентгеновского 9.
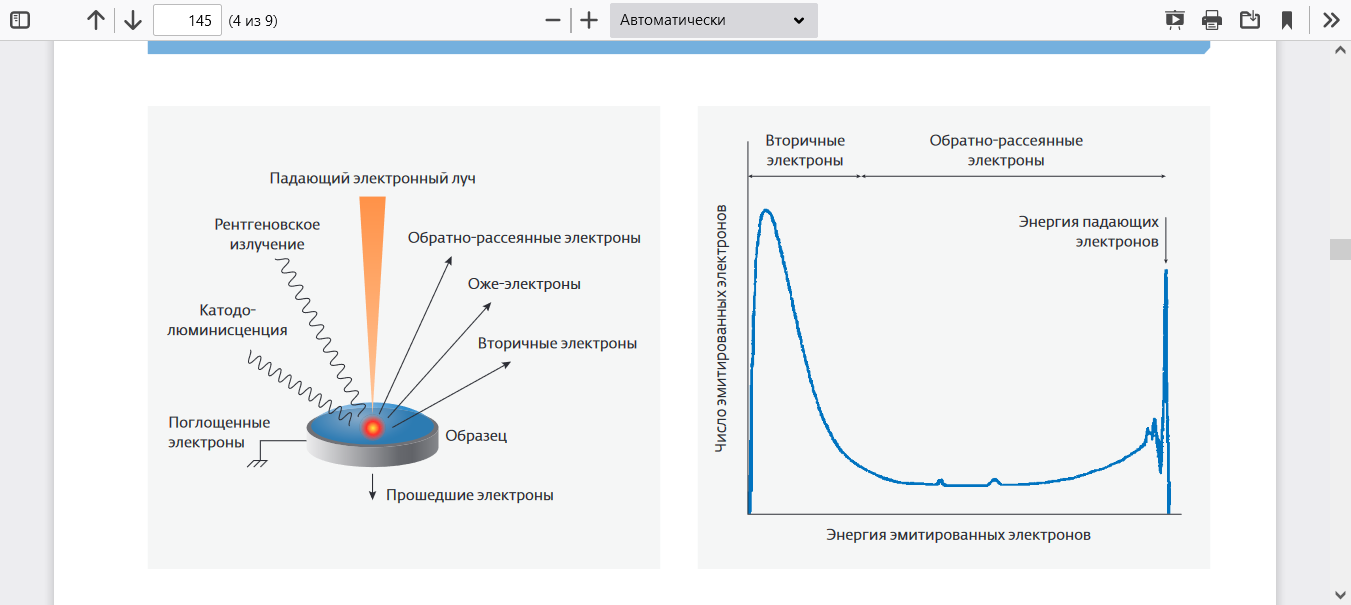
Рисунок 1 Взаимодействие пучка электронов с поверхностью объекта исследования.
Важнейшей характеристикой любого микроскопа является его разрешающая способность.6.
Она определяется:
1 - площадью сечения или диаметром зонда,
2 - контрастом, создаваемым образцом и детекторной системой,
3 - областью генерации сигнала в образце.
Диаметр зонда в основном зависит от конструктивных особенностей и качества узлов микроскопа и прежде всего электронной оптики. В современных РЭМ достигнуто высокое совершенство компонентов конструкции, что позволило уменьшить диаметр зонда до 5...10 нм.
Формирование контраста в РЭМ определяется разностью детектируемых сигналов от соседних участков образца, чем она больше, тем выше контраст изображения. Контраст зависит от нескольких факторов: топографии поверхности, химического состава объекта, поверхностных локальных магнитных и электрических полей, кристаллографической ориентации элементов структуры. Важнейшими из них являются топографический, зависящий от неровностей поверхности образца, а также композиционный, зависящий от химического состава. Уровень контраста определяется также и эффективностью преобразования падающего на детектор излучения, которое создает сигнал на его выходе.
Другой фактор, ограничивающий разрешение, зависит от размеров области генерации сигнала в образце. Схема генерации различных излучений при воздействии электронного пучка на образец представлена на рисунке 2. При проникновении первичных электронов в образец они рассеиваются во всех направлениях, поэтому внутри образца происходит расширение пучка электронов.
Отраженные электроны. Они образуются при рассеивании первичных электронов на большие (до 90o) углы в результате однократного упругого рассеивания или в результате многократного рассеивания на малые углы. В конечном итоге первичные электроны, испытав ряд взаимодействий с атомами образца и теряя при этом энергию, изменяют траекторию своего движения и покидают поверхность образца. Протяженность области возрастает с увеличением ускоряющего первичные электроны напряжения и уменьшения среднего атомного номера Z элементов, входящих в состав образца. Размеры области генерации отраженных электронов значительны и зависят от длины пробега электронов в материале образца. Протяженность области может изменяться от 0,1 до 1 мкм.
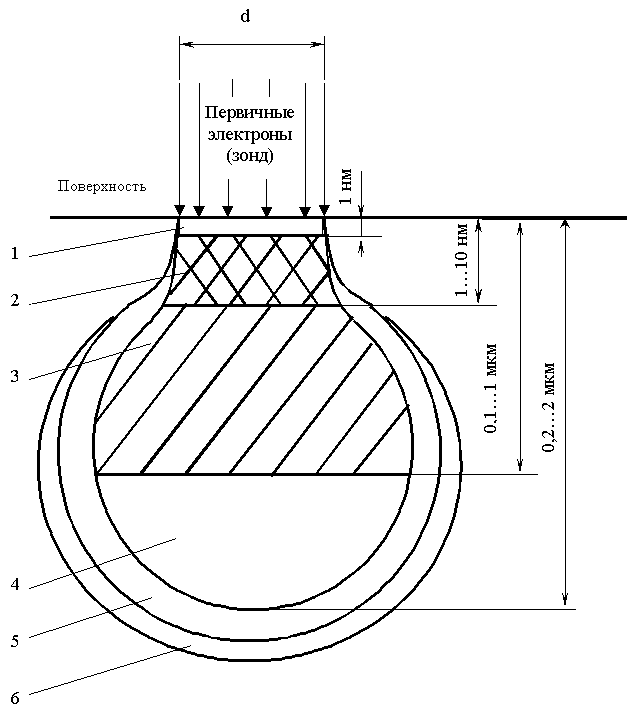
Рисунок 2 Области сигналов и пространственное разрешение при облучении поверхности объекта потоком электронов (зонд). Области генерации: 1 – Оже-электронов, 2 – вторичных электронов, 3 – отраженных электронов, 4 – характеристического рентгеновского излучения, 5 – тормозного рентгеновского излучения, 6 – флуоресценции.
Вторичные электроны. Первичные электроны, проникающие в образец, взаимодействуют с электронами внешних оболочек атомов объекта, передавая им часть своей энергии. Происходит ионизация атомов образца, а высвобождающиеся в этом случае электроны могут покинуть образец и быть выявлены в виде вторичных электронов. Они характеризуются очень малой энергией до 50 эВ и поэтому выходят из участков образца очень близких к поверхности (рисунок 2). Глубина слоя, дающего вторичные электроны, составляет 1...10 нм. При получении изображений во вторичных электронах разрешающая способность определяется прежде всего диаметром первичного зонда. Вторичные электроны обеспечивают максимальную в сравнении с другими сигналами разрешающую способность порядка 5...10 нм. Поэтому они являются в РЭМ главным источником информации для получения изображения поверхности объекта, и именно для этого случая приводятся паспортные характеристики прибора. Количество образующихся вторичных электронов слабо зависит от атомного номера элемента. Основным параметром, определяющим выход вторичных электронов, является угол падения пучка первичных электронов на поверхность объекта.
Поглощенные электроны. При воздействии зонда часть генерируемых электронов остается в объеме образца (рисунок 2). Оставшиеся электроны образуют ток поглощенных электронов (рисунок 1). Его величина равна разности между током зонда и токами отраженных и вторичных электронов. Эта разность является сигналом для получения изображения, на которое оказывают влияние как топографический, так и композиционный эффекты.
2. АНАЛИЗ ПРИНЦИПА РАБОТЫ И ОСОБЕННОСТИ КОНСТРУКЦИИ РАСТРОВОГО ЭЛЕКТРОННОГО МИКРОСКОПА
Принцип действия любого РЭМ основывается на анализе вторичных или отраженных электронов, возникающих при взаимодействии электронного зонда с веществом. При этом в основу формирования изображения поверхности изучаемого объекта положен способ телевизионной развертки посредством сканирования первичного пучка электронов по поверхности образца. Изображение строится последовательно, путем сканирования образца сфокусированным электронным пучком по определенной траектории от точки к точке. Зондом в РЭМ является тонкий пучок электронов диаметром менее 1 нм, который сканирует образец под действием магнитной отклоняющей системы. .[6]
Испускаемые из каждой точки частицы – электроны (вторичные и отраженные), оптические и рентгеновские кванты – улавливаются соответствующими детекторами. Сигналы с детекторов усиливаются и формируются в двумерную матрицу, которая отображается на мониторе компьютера.
Растровый электронный микроскоп состоит из следующих основных блоков и модулей: источника электронов (эмиттер, катодный узел, электронная пушка), электронно-оптической системы (конденсорная и объективная линзы, система отклонения, стигматоры, корректоры, диафрагмы и.т.д.) для фокусировки первичного пучка электронов и управления сканированием, формирующей электронный зонд и обеспечивающей его сканирование на поверхности образца, системы, формирующей изображение.
Растровый электронный микроскоп является вакуумным прибором, так как при нормальном атмосферном давлении электронный пучок сильно рассеивается и поглощается, что делает невозможным его фокусировку. РЭМ имеет в вакуумную камеру, которая служит для создания необходимого разряжения (
10-3 Па) в рабочем объеме электронной пушки и электронно-оптической системы.
Функциональная схема растрового электронного микроскопа также включает себя:
аналитическую камеру с образцом;
детекторы для регистрации вторичного сигнала;
систему управления и сбора данных;
систему откачки для создания вакуума в аналитической камере.
Составными частями микроскопа являются механические узлы (шлюзы, гониометрический стол и т.д.), обеспечивающие установку и перемещение образца.[6]
Источником электронов в растровом электронном микроскопе является электронная «пушка», состоящая из эмиттера электронов (катода), покинув который электроны затем ускоряются при движении к образцу.
Основные узлы растрового электронного микроскопа приведены на рисунке 3.
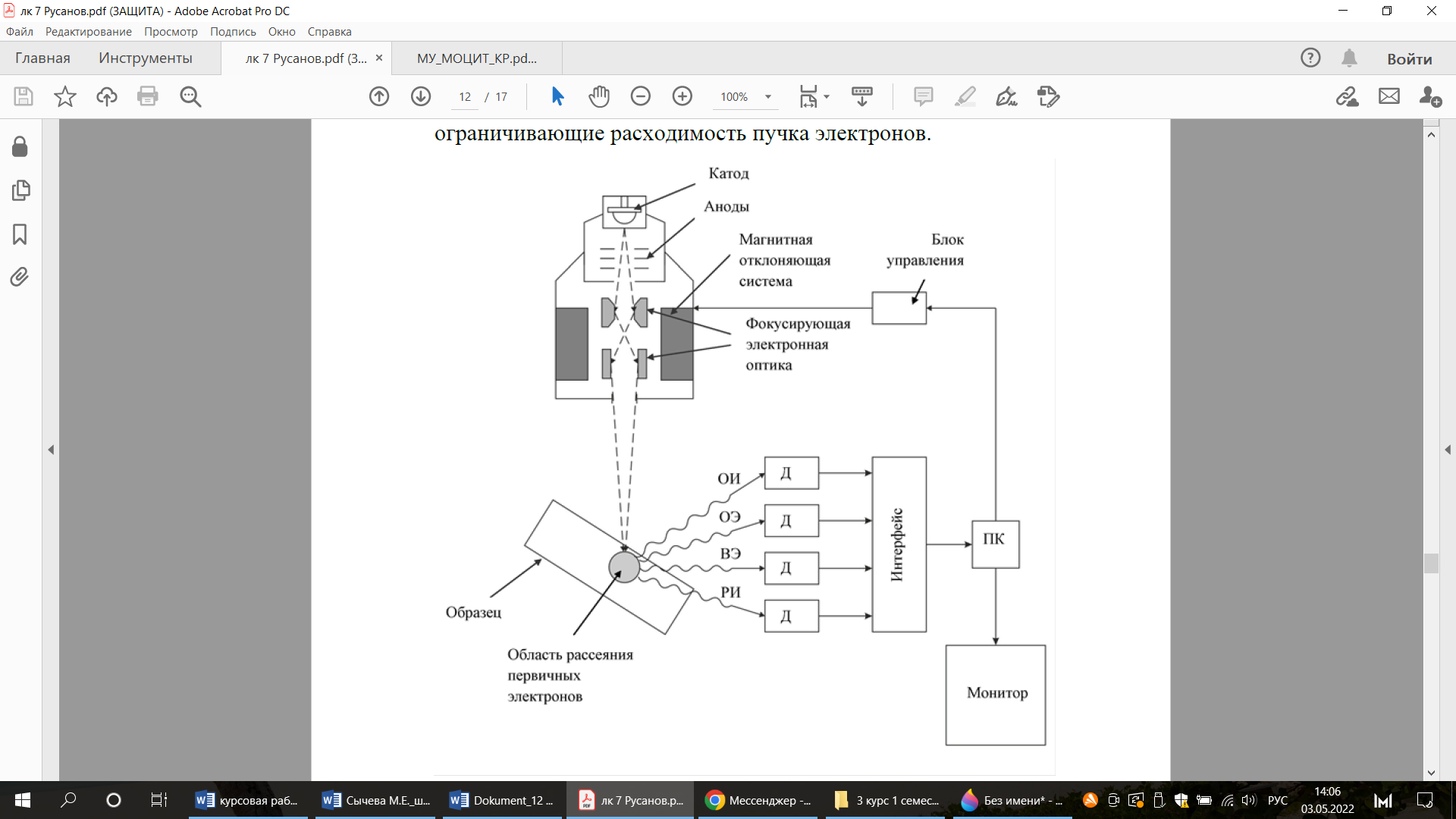
Рисунок 3 Основные узлы растрового электронного микроскопа
Электронная пушка состоит из катода и анодов. Обычно в качестве катода используется вольфрамовая V-образная проволока в форме шпильки и закрепленную в керамическом цоколе, обеспечивающем легкую замену катода в случае перегорания нити.

Рисунок 4 - Устройство электронной пушки термоэмиссионного типа
При нагревании до температуры примерно 2800 K катода, сделанного из вольфрамовой проволоки диаметром около 0,1 мм, возникает эмиссия электронов с его поверхности. Электроны ускоряются напряжением, приложенным между катодом и анодом, которое можно изменять от 1 до 50 кВ. Пучок электронов от пушки проходит через электромагнитные линзы. Фокусировка потока электронов осуществляется магнитным полем, имеющим осевую симметрию. Оно создается электромагнитной линзой, которая представляет собой соленоид. Магнитное поле возникает при пропускании электрического тока через обмотку соленоида, концентрируется с помощью так называемого полюсного наконечника и воздействует на проходящий через него поток электронов. Фокусное расстояние линзы можно плавно регулировать путем изменения силы тока в обмотке соленоида. B системе имеются диафрагмы, ограничивающие расходимость пучка электронов.[7]
Электронная пушка является одним из основных конструктивных элементов электронно-оптической системы растровых микроскопов и предназначена для генерации пучка электронов с энергиями, достаточными для выбивания вторичных электронов из исследуемого вещества. Материал катода, тип эмиссии и конструктивные особенности электронной пушки определяют два основных параметра электронного пучка – величину тока и размер пятна на поверхности образца (площадь сечения электронного пучка), которые в свою очередь влияют на разрешение микроскопа для большинства механизмов формирования контраста.
В современных электронно-оптических колоннах используется система из нескольких конденсорных линз и отклоняющих систем, а также устройства для компенсации астигматизма (стигматоры) и юстировки пучка относительно оптической оси колонны (корректоры).
Для работы РЭМ необходим тонкий электронный пучок (зонд). Можно варьировать диаметр электронного пучка, если поместить на выходе электронной пушки регулируемое магнитное поле, создаваемое элементами электронной оптики. Поток электронов из электронной пушки регулируется двухкаскадной электромагнитной системой, включающей линзы конденсора и объектива. В результате на поверхности образца фокусируется тонкий электронный зонд (рисунок 5).
Усиление или ослабление возбуждения линзы конденсора (значения магнитной индукции в ней) позволяет изменять толщину электронного пучка. Если использовать всю открытую область объективной линзы, невозможно получить тонкий электронный зонд из-за сферических аберраций. Чтобы снизить их влияние, между линзой конденсора и линзой объектива размещается тонкая металлическая пластина с небольшим отверстием – апертура. Через нее должна проходить только та часть электронного луча, которая следует через центр объективной линзы. Смещение апертуры относительно центра объективной линзы приводит к значительному увеличению аберраций, и формирование тонкого электронного зонда становится невозможным. Поэтому центр апертуры объективной линзы должен располагаться строго на оптической оси.

Рисунок 5 - Формирование зонда электронными линзам
При увеличении возбуждения линзы конденсора электронный пучок, падающий на апертуру, значительно расширяется, поэтому число электронов (величина тока зонда), достигающих линзы объектива, уменьшается. И, наоборот, при уменьшении возбуждения пучок электронов расширяется не столь значительно и большая доля электронов, проходя через апертуру, достигает линзы объектива. Таким образом, настраивая уровень возбуждения линзы конденсора, можно изменять диаметр электронного зонда и его ток.
В основе работы всех элементов электронной оптики лежит изменение траектории электронов под действием электрического или магнитного поля. Изменяя величину напряжения или тока можно изменить фокусное расстояние (оптическую силу) линзы. Именно этот эффект используется при фокусировке электронного пучка на поверхности образца. .[7]
Образец крепится на предметном столике, который может перемещаться в трех взаимно перпендикулярных направлениях, допускает наклон образца до 90o к электронно-оптической оси и вращение вокруг оси от 0 до 360o. Электронный пучок, сфокусированный на поверхности образца, вызывает появление отраженных, вторичных и поглощенных электронов, которые используются для получения изображения поверхности образца. Эти сигналы улавливаются специальными детекторами. В детекторе поток электронов преобразуется в электрический сигнал (ток).
В качестве детектора вторичных электронов используется детектор Эверхарта-Торнли. Схема детектора представлена на рисунке 6. Коллектор 1 имеет положительный потенциал, приблизительно +250 В, благодаря чему траектории вторичных электронов искривляются, и они попадают в коллектор. На первичные и отраженные электроны, имеющие высокие значения энергии, этот потенциал существенного влияния не оказывает.
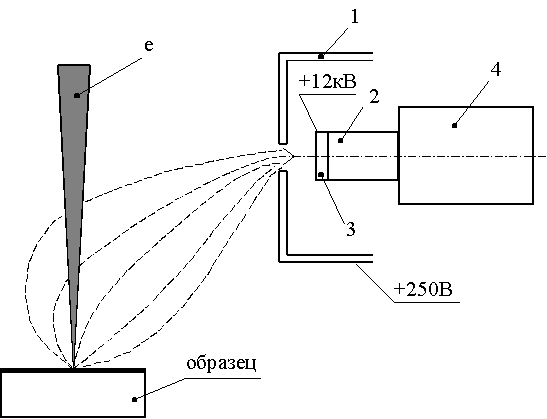
Рисунок 6 Схема детектора эмитированных электронов Эверхарта-Торнли
1 – коллектор, 2 – световод, 3 – сцинтиллятор, 4 – фотоумножитель.
Для регистрации отраженных электронов обычно используются твердотельные детекторы (полупроводниковые, микроканальные пластины). Эффективность сбора отраженных электронов зависит от угла наклона детектора к поверхности генерации электронов и расстояния между ними.
Для рентгеновского излучения существует два типа детекторов: энергодисперсионный и волнодисперсионный. Энергодисперсионный детектор использует корпускулярные свойства рентгеновского кванта и представляет собой полупроводниковый диод. Волнодисперсионный детектор использует дифракцию рентгеновского излучения на кристалле-анализаторе, с последующей регистрацией пропорциональным счетчиком. .[6]
Сканирующие электронные микроскопы с экстремально высоким разрешением (XHR SEM) семейства Magellan - новый класс инструментов компании FEI Company. Семейство микроскопов Magellan XHR SEM позволяет ученым и инженерам видеть трехмерные изображения поверхностей образцов под различными углами при разрешениях менее одного нанометра (порядка размеров десяти атомов водорода, выстроенных рядом в линейку).8
Микроскопы Magellan XHR SEM обеспечивают визуализацию образцов при очень низких энергиях электронного пучка. Благодаря этому отсутстуют искажения, которые неизбежны при проникновении высокоэнергетичных электронов в материал.
Функциональность и производительность семейства Magellan обеспечена интеграцией новых электронных оптических элементов, технологией электронной пушки, высокоточным пяти-осевым пьезо-керамическим лабораторным столом и высокостабильной платформой с конфигурируемой аналитической камерой. https://sernia.ru/upload/pdf_files/Magellan_xhr_sem.pdf
Семейство Magellan включает в себя две модели: Magellan 400 оптимизирована для научных исследований, а Magellan 400L — для полупроводниковых лабораторий.
Характеристики растрового электронного микроскопа Magellan XHR SEM.
Разрешение при оптимальной рабочей дистанции
(0,8 нм при 15 кВ; 0,8 нм при 2 кВ; 0,9 нм при 1 кВ; 1,5 нм при 200 В;)
Разрешение в точке схождения
(0,8 нм при 15 кВ; 0,9 нм при 5 кВ; 1,2 нм при 1 кВ;
3. ИДЕНТИФИКАЦИЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ КРИТЕРИЕМ СОГЛАСИЯ ПИРСОНА
Таблица 1 – Результаты измерений растровым электронным микроскопом строки нанообъекта
№
|
Линейный размер, нм
|
1
|
47,58
|
2
|
48,15
|
3
|
48,95
|
4
|
52,41
|
5
|
48,50
|
6
|
51,77
|
7
|
49,79
|
8
|
48,56
|
9
|
52,12
|
10
|
52,97
|
11
|
52,81
|
12
|
49,71
|
13
|
48,45
|
14
|
49,79
|
Для определения соответствия эмпирического распределения как нормальному, так и любому другому теоретическому распределению, чаще всего используется критерий согласия Пирсона (критерий «χ -квадрат»).
Данный критерий, как и любой другой, не доказывает правдивость выдвинутой гипотезы, a лишь устанавливает на принятом уровне доверительной вероятности ее соответствие или несоответствие результатам измерений.
В качестве критерия проверки гипотезы используется случайная величина:
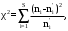 (3.1) (3.1)
Где n'i- теоретические частоты, ni-эмпирические частоты. Определение теоретических частот может производиться согласно предыдущему способу.
Установлено, что при n→∞ по закон распределения случайной величины независимо от закона распределения результатов измерений, стремится к закону степенями свободы k = S-1-r, где S – число частичных интервалов, г- число параметров предполагаемого распределения. Для нормального распределения в общем случае r = 2 (оценивают математическое ожидание и среднее квадратическое отклонение), соответственно k = S– 3.
Вычислив χ2 и определив k, по таблице распределений χ2 в зависимости от выбранного значения уровня значимости α =1– P (P-Доверительная вероятность) находятся границы χ2 (k; ɑ) и χ2 (k; 1 – α). Если выполняется условие χ2 (k; α) < χ2 < χ2 (k:1 – α), то эмпирическое распределение не противоречит теоретическому с вероятностью Р.
Сначала найдём частоты эмпирического распределения:
Расположим результаты измерения в порядке возрастания:
47,58 48,15 48,45 48,50 48,56 48,95 49,71 49,79 49,79 51,77 52,12 52,41 52,81 52,97
Диапазон изменения значений результатов измерений разбивается на r интервалов по формуле Стерджесса
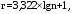 (3.2) (3.2)
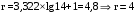
Ширина интервалов
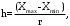 (3.3) (3.3)
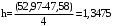
Определяются границы интервалов так, чтобы верхняя граница j-го интервала была равна: 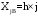 , а его нижняя граница совпадала с верхней границей (j-1)-го интервала: , а его нижняя граница совпадала с верхней границей (j-1)-го интервала: 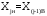
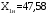 ; ;
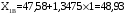 ; ;
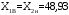 ; ;
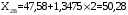 ; ;
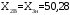 ; ;
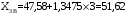 ; ;
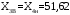 ; ;
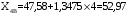 ; ;
Определяется число результатов измерений, попавших в заданный j-й интервал по условию XjН < Xi ≤ XjВ. Числа результатов измерений nj называют частотами, а их отношения к общему числу результатов измерений относительными частотами
Найдем середины интервалов и относительные частоты:
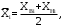 (3.4) (3.4)
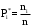 , (3.5) , (3.5)
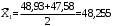 ; ;
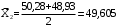
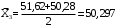
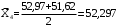
Таблица 2- Результаты расчетов эмпирической частоты
Номер
интервала
|
Граница интервала
|
Частота
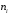
|
Серединный интервал
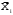
|
Относительные частоты
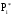
|
Xн
|
Xв
|
1
|
2
|
3
|
4
|
5
|
6
|
1
|
47,58
|
48,93
|
5
|
48,255
|
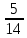
|
2
|
48,93
|
50,28
|
4
|
49,605
|
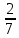
|
Продолжение таблицы 2
1
|
2
|
3
|
4
|
5
|
6
|
2
|
48,93
|
50,28
|
4
|
49,605
|
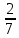
|
3
|
50,28
|
51,62
|
0
|
50,952
|
0
|
4
|
51,62
|
52,97
|
5
|
52,297
|
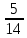
|
Потом находим теоретические частоты:
Определим параметры предполагаемого (теоретического) нормального закона распределения.
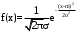 , (3.6) , (3.6)
Оценку математического ожидания найдем по формуле
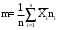 , (3.7) , (3.7)
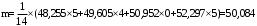
Оценку дисперсии вычислим по формулам
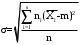 , (3.8) , (3.8)
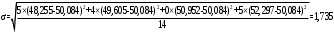
Переходим к новой переменной Zi и вычисляют концы интервалов
При этом наименьшее значение, т. е.XН1, полагаем равным ∞, а наибольшее, т. е. XВ4, полагаем равным +∞.
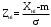 , (3.9) , (3.9)
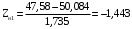
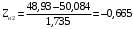
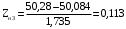
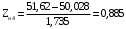
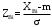 , (3.10) , (3.10)
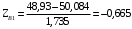
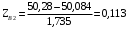
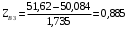
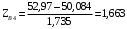
Таблица 3-Результаты расчётов интервалов с переменной Zi
Номер интервала
|
Zнi
|
ZВi
|
1
|
-∞
|
-0,665
|
2
|
-0,665
|
0,113
|
3
|
0,113
|
0,885
|
4
|
0,885
|
+∞
|
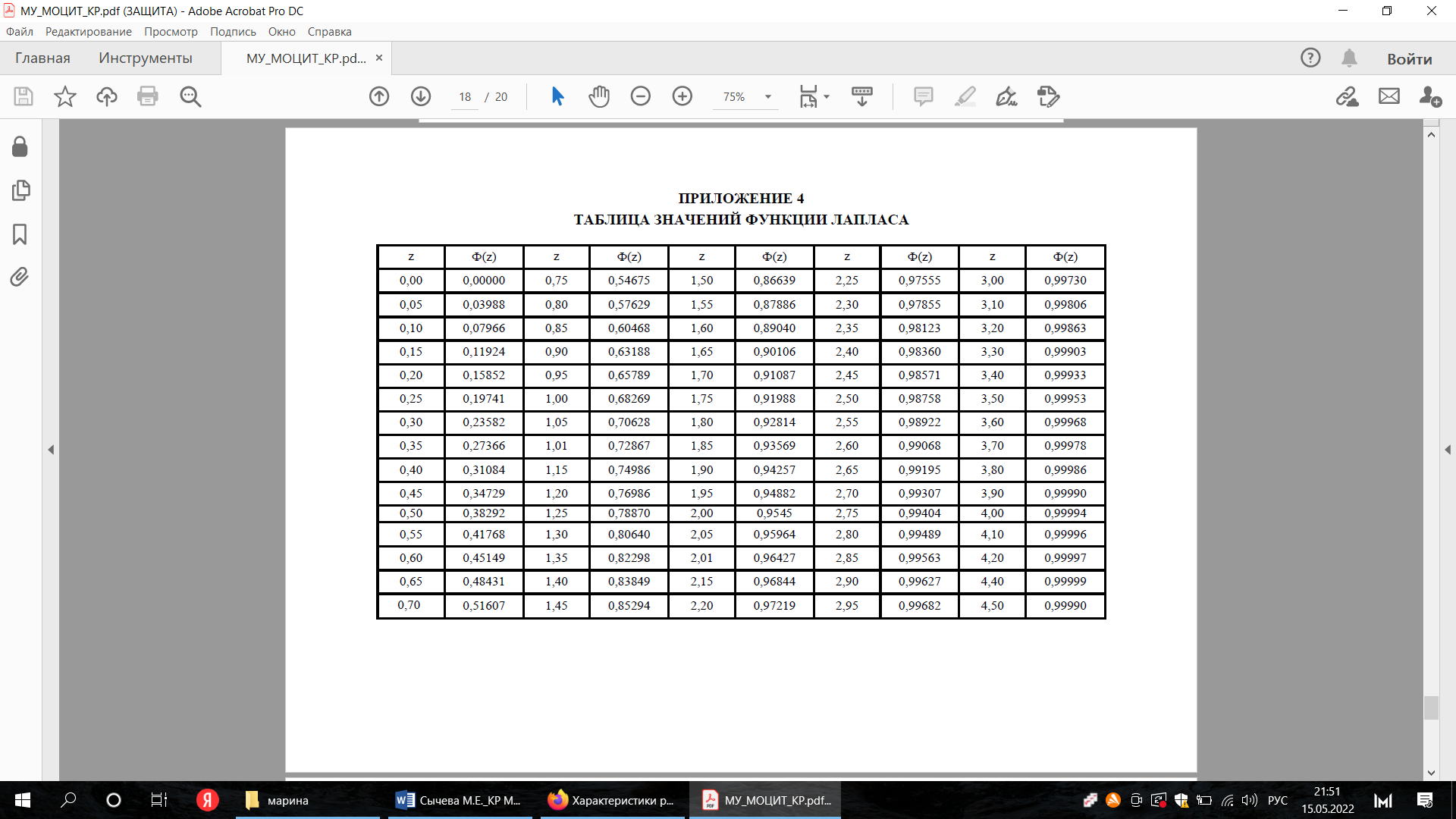
Выполним расчет теоретических частот 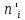 по формуле . Для вычисления вероятностей Pi по формуле воспользуемся таблицей Лапласа Приложения со значениями нормальной стандартной функции распределения. по формуле . Для вычисления вероятностей Pi по формуле воспользуемся таблицей Лапласа Приложения со значениями нормальной стандартной функции распределения.
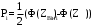 , (3.11) , (3.11)
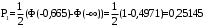
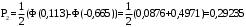
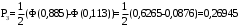
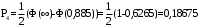
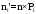 , (3.12) , (3.12)
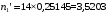
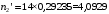
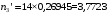
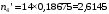
По формуле (3.1) найдём значение χ2
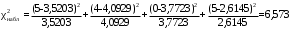
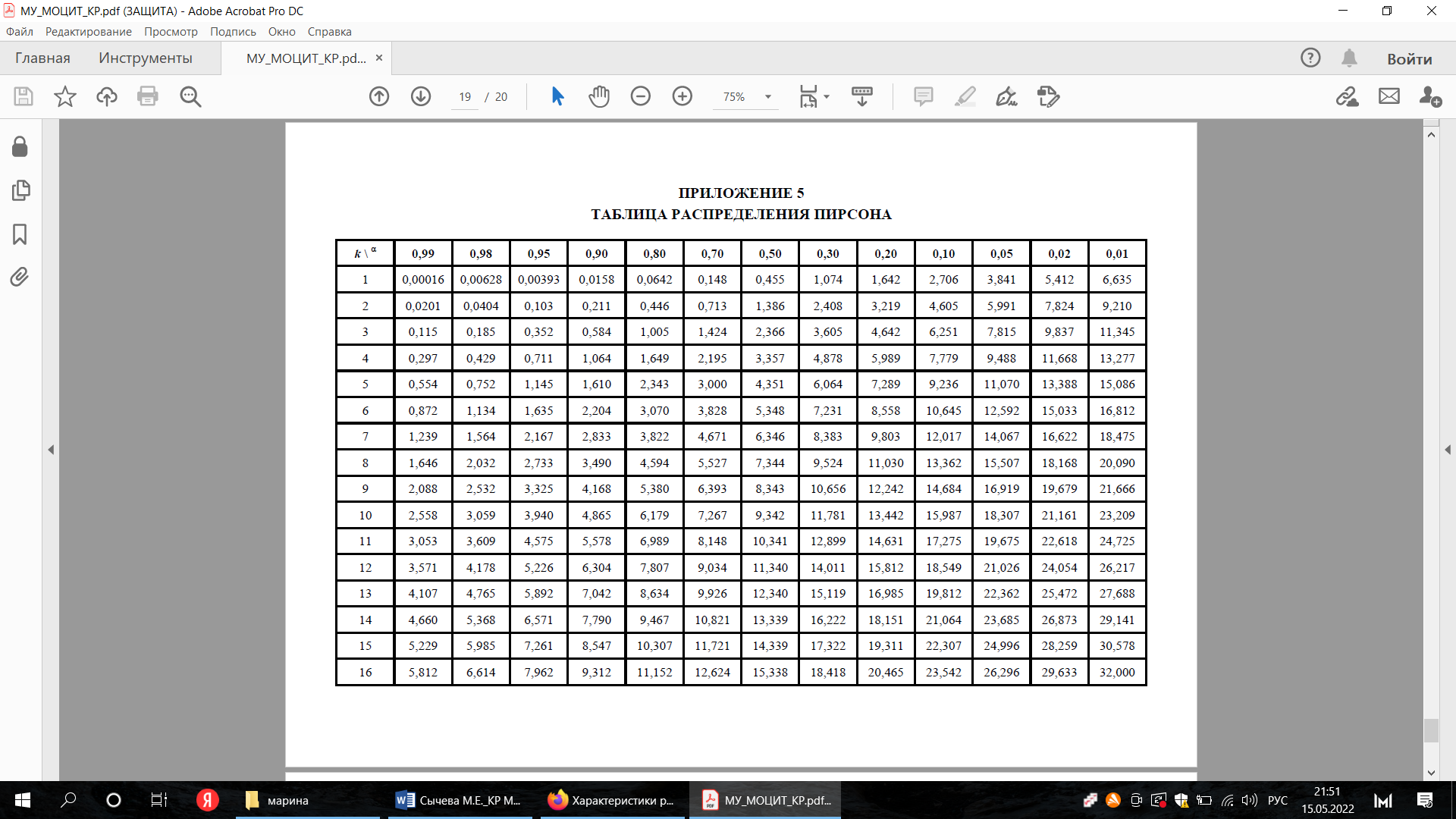
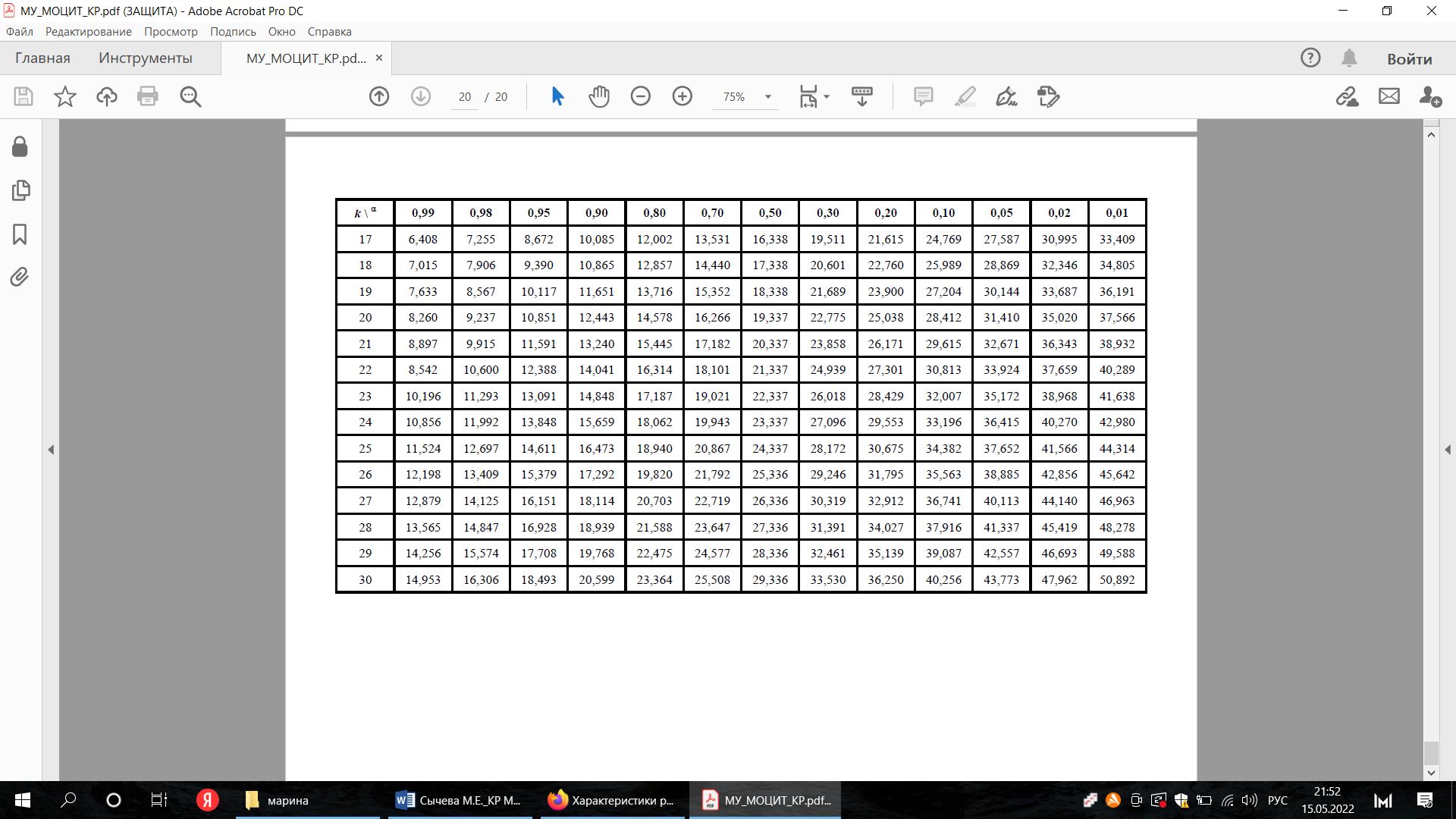
По таблице квантилей распределения χ2 (см. таблицу в Приложения) с числом степеней свободы k = 4– 3= 1 находим, что χ2табл = 6,635 для α =1– 0,99=0,01 и χ2 табл = 0,00016 для α=0,99.
Поскольку (0,00016 < 6,573 < 6,635), то можно считать, что гипотеза о нормальном законе распределении измерений растровым электронным микроскопом строки нанообъекта не противоречит теоретическому нормальному закону распределения с вероятностью Р = 0,99.
ЗАКЛЮЧЕНИЕ
В настоящее время аппаратура и методы растровой электронной микроскопии применяются практически во всех естественнонаучных исследованиях и для контроля в условиях производства. Развитие полупроводниковой микро-, нано-, оптоэлектроники стимулировало появление и развитие новых методов растровой микроскопии, основанных на таких явлениях, как генерация, диффузия, рекомбинация электронно-дырочных пар, полевая зависимость вторичных электронов и др.
Помимо традиционного применения растровой электронной микроскопии как метода наблюдения и получения изображения исследуемого объекта с большим увеличением и высоким разрешением он становится методом, позволяющим получить количественную информацию об электрофизических, геометрических параметрах, параметрах реальной кристаллической структуры, фазовом и химическом составе, структуре энергетических уровней и т.д.
Популярность и широкое применение растровой электронной микроскопии обусловлены совокупностью уникальных возможностей, присущих этому методу: получение трехмерных изображений широкого спектра материалов с большой глубиной фокуса 9, простотой применения 10, высокая скорость получения изображения «области интереса» и проведения качественного и количественного анализа химического состава образца 11, высоким пространственном разрешением, достигающее 1 нм 12, использование различных детекторов, значительно расширяющих диапазон получаемых данных 13, 14,15.
Поэтому, поставленная цель курсовой работы - изучение использования растровой электронной микроскопии в нанометровом и микрометровом масштабе, на сегодняшний день является актуальной и необходимой.
В ходе написания курсовой работы были рассмотрены следующие задачи, связанные с изучением физических основ растровой электронной микроскопии, проанализирован принцип работы основных блоков растрового электронного микроскопа, изучены особенности конструкции растрового электронного микроскопа. На основании полученных результатов измерений растровым электронным микроскопом строки нанообъекта выполнена идентификация функции распределения результатов измерения.
Современный РЭМ — это сложный прибор высокого технического уровня, включающий несколько основных систем: электронно-оптическую систему, позволяющую получить разрешение вплоть до 10Å при токах электронного пучка 10-11–10-12 Å; вакуумную систему, обеспечивающую вакуум 2×10-6 торр; систему детектирования различных сигналов с малошумящим многоканальным усилительным трактом; прецизионную механическую систему перемещения объекта; систему сбора и обработки информации с визуализацией и фотографированием изображения. Конструкция РЭМ оснащается спектрометрами с дисперсией по длинам волн и по энергиям для реализации метода рентгеноспектрального микроанализа, устанавливается устройство сбора и вывода катодолюминесцентного излучения 16.
В процессе выполнения курсовой работы была выполнена проверка соответствия эмпирического распределения результатов измерений растровым электронным микроскопом строки нанообъекта нормальному теоретическому закону распределения на основе критериев согласия Пирсона.
Для этого был выполнен расчет частот теоретического и эмпирического распределения. В результате расчетов было получено расчетное значение критерия Пирсона. Расчетный критерий для нормального распределения составил χ2набл = 6,573 при количестве степеней свободы 1. Табличное значение критерия Пирсона равно χ2табл = 6,635. По таблице квантилей распределения χ2 с числом степеней свободы k = 4– 3= 1 были определены границы: χ2табл = 6,635 для α =1– 0,99=0,01 и χ2табл = 0,00016 для α=0,99.
Так как выполняется условие χ2табл(k,α) ≤ χ2набл ≤ χ2табл(k,1α): (0,00016 < 6,573 < 6,635), то гипотеза о нормальном законе распределении результатов измерений растровым электронным микроскопом строки нанообъекта не противоречит теоретическому нормальному закону распределения с вероятностью Р=0,99.
СПИСОК ЛИТЕРАТУРЫ
Чжоу, У. Сканирующая микроскопия для нанотехнологий / У. Чжоу, З. Л. Ван. –Нью–Йорк : Спрингер, 2007. - 522 с. – http://dx.doi.org/10.1007/978-0-387-39620-0.
ГОСТ Р 8.631-2007. ГСИ. Микроскопы электронные растровые. Методика поверки. https://docs.cntd.ru/document/1200050773 (дата обращения: 14.05.2022 г).
С. Г. Конников Количественная растровая электронная микроскопия материалов и структур твердотельной электроники // Научное приборостроение, 2000, том 10, No 1, c. 3–13
ГОСТ ISO/TS 80004-6-2017 Нанотехнологии. Часть 6 Характеристики нанообъектов и методы их определения. Термины и определения https://docs.cntd.ru/document/1200141447
Анцыферов С.С., Афанасьев М.С., Русанов К.Е. Обработка результатов измерений: Учебное пособие. М: Издательство ИКАР, 2014 г.228 с.
Быков Ю.А., Карпухин С.Д. Растровая электронная микроскопия и рентгеноспектральный микроанализ. Аппаратура, принцип работы, применение: учеб. пособие по курсу "Современные методы исследования структуры материала" / Под ред. Ю.А. Быкова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2010, с.44
Теоретические основы растровой электронной микроскопии и энергодисперсионного анализа наноматериалов : учеб. пособие /[Д. А. Полонянкин и др.] ; Минобрнауки России, ОмГТУ. – Омск : Изд-во ОмГТУ, 2019. – 116 с. : ил.
А.Ляпин, к.г.-м.н. Визуализация тонких структур –современные технологии Часть 2 https://www.electronics.ru/files/article_pdf/4/article_4721_695.pdf (дата обращения 14 мая 2022 г.)
http://www.rusnanonet.ru/articles/34482 (дата обращения 14 мая 2022 г.)
(http://www.smalltimes.com)
Есида, А. Сканирующая электронная микроскопия / А. Есида, Ю. Кабураги, Ю. Хисияма // Материаловедение и технология углерода: характеристика. –2016. – Ч. 5. – С. 71-93. – http://dx.doi.org/10.1016/B978-0-12-805256-3.00005-2 . Yoshida, A. Scanning electron microscopy / A. Yoshida, Y. Kaburagi, Y. Hishiyama // Materials science and engineering of carbon: Characterization. –2016. – Ch. 5. – P. 71–93. – http://dx.doi.org/10.1016/B978-0-12-805256-3.00005-2.
Сканирующая электронная микроскопия / Л. Реймер. – Берлин : Springer Heidelberg, 1998. – 528 с. – http://dx.doi.org/10.1007/978-3-540-38967-5 . Scanning Electron Microscopy / L. Reimer. – Berlin : Springer Heidelberg, 1998. – 528 p. – http://dx.doi.org/10.1007/978-3-540-38967-5.
Симидзу К. Новые горизонты прикладной сканирующей электронной микроскопии. Серия Спрингера в области наук о поверхности / К. Симидзу, Т. Митани. – Берлин : Springer Heidelberg,2010. – 179 с. – http://dx.doi.org/10.1007/978-3-642-03160-1 Shimizu, K. New Horizons of Applied Scanning Electron Microscopy. Springer Series in Surface Sciences / K. Shimizu, T. Mitani. – Berlin : Springer Heidelberg, 2010. – 179 p. – http://dx.doi.org/10.1007/978-3-642-03160-1
Фогт Т. Моделирование наноразмерных изображений в электронной микроскопии. Наноструктура Наука и техника / Т. Фогт, В. Дамен, П. Бинев. – Бостон : Springer US, 2012. – 182 с. – http://dx.doi.org/10.1007/978-1-4614-2191-7 . Vogt, T. Modeling Nanoscale Imaging in Electron Microscopy. Nanostructure Science and Technology / T. Vogt, W. Dahmen, P. Binev. – Boston : Springer US, 2012. – 182 p. – http://dx.doi.org/10.1007/978-1-4614-2191-7
Шварц, А. Дж. Дифракция обратного рассеяния электронов в материаловедении /А. Дж. Шварц, М. Кумар, Б. Л. Адамс, Д. П. Филд. – Бостон : Springer US, 2009. –403 с. – https://doi.org/10.1007/978-0-387-88136-2 . Schwartz, A. J. Electron Backscatter Diffraction in Materials Science /A. J. Schwartz, M. Kumar, B. L. Adams, D. P. Field. – Boston : Springer US, 2009. –403 p. – https://doi.org/10.1007/978-0-387-88136-2.
Справочник по анализу поверхности и границ раздела / М. Кигучи. – Сингапур :Springer Nature, 2018. – 853 с. – http://dx.doi.org/10.1007/978-981-10-6156-1 . Compendium of Surface and Interface Analysis / M. Kiguchi. – Singapore :Springer Nature, 2018. – 853 p. – http://dx.doi.org/10.1007/978-981-10-6156-1.
Характеристика микроструктур методом аналитической электронной микроскопии (AEM) / Ю. Ронг. – Берлин : Springer Heidelberg, 2012. – 552 с. –http://dx.doi.org/10.1007/978-3-642-20119-6 . Characterization of Microstructures by Analytical Electron Microscopy (AEM) / Y. Rong. – Berlin : Springer Heidelberg, 2012. – 552 p. –http://dx.doi.org/10.1007/978-3-642-20119-6.
С. Г. Конников Количественная растровая электронная микроскопия материалов и структур твердотельной электроники // Научное приборостроение, 2000, том 10, No 1, c. 3–13
ПРИЛОЖЕНИЕ 1
ПРИЛОЖЕНИЕ 2
|
|
|
 Скачать 1.59 Mb.
Скачать 1.59 Mb.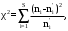 (3.1)
(3.1)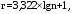 (3.2)
(3.2)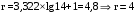
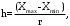 (3.3)
(3.3)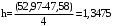
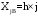 , а его нижняя граница совпадала с верхней границей (j-1)-го интервала:
, а его нижняя граница совпадала с верхней границей (j-1)-го интервала: 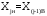
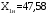 ;
;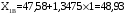 ;
;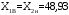 ;
;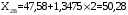 ;
;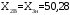 ;
;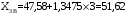 ;
;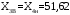 ;
;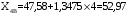 ;
;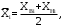 (3.4)
(3.4)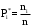 , (3.5)
, (3.5)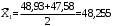 ;
;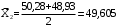
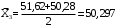
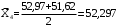
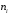
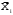
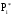
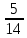
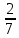
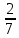
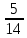
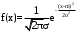 , (3.6)
, (3.6)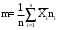 , (3.7)
, (3.7)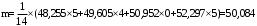
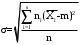 , (3.8)
, (3.8)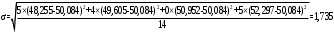
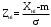 , (3.9)
, (3.9)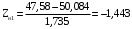
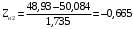
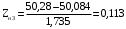
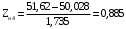
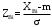 , (3.10)
, (3.10)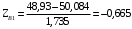
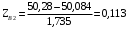
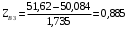
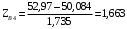
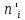 по формуле . Для вычисления вероятностей Pi по формуле воспользуемся таблицей Лапласа Приложения со значениями нормальной стандартной функции распределения.
по формуле . Для вычисления вероятностей Pi по формуле воспользуемся таблицей Лапласа Приложения со значениями нормальной стандартной функции распределения. 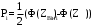 , (3.11)
, (3.11)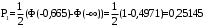
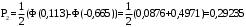
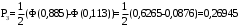
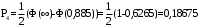
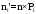 , (3.12)
, (3.12)