абдулмухамен. 1. Описание первой модели влияния отказов элементов на состояние системы
 Скачать 343.19 Kb. Скачать 343.19 Kb.
|
 ВведениеГраницы применимости булевых моделей при анализе надежности систем, состоящих из элементов, которые могут находиться в трех состояниях, существенно расширяются при построении логико-вероятностных моделей с использованием алгебры несовместных событий. В работе Б.Диллона и Ч.Сингха свойство несовместности упоминается, но вывод основных формул основан на анализе перебора всех возможных состояний систем, а не на особенностях алгебры несовместных событий. Алгебра несовместных событий фрагментально рассматривается в работе К.Шеннона для демонстрация логической записи условий реализации зависимых событий. Элементы алгебры групп несовместных событий (ГНС), для случая несовместности прямых исходов событий приведены , для случая несовместности инверсных исходов событий . Примеры использования полиномиального разложения для анализа надежности сложных структур с элементами, которые могут находиться в трех состояниях. В данной статье описывается технология программной реализации алгебры ГНС в программном комплексе АРБИТР, позволяющая решать задачи анализа надежности сложных структур при различных моделях влияния отказов типа «Обрыв» и «Замыкание» на состояние системы. 1.Описание первой модели влияния отказов элементов на состояние системы. В работе Б.Диллона и Ч.Сингха предложена следующая модель влияния отказов элементов на состояние системы: а) для последовательного соединения отказ хотя бы одного из элементов типа «Обрыв» приводит к отказу всей системы, отказ всех элементов типа «Замыкание» приводит к отказу системы, отказ нескольких элементов типа «Замыкание» при наличии хотя бы одного работоспособного элемента не приводит к отказу системы; б) для параллельного соединения отказ хотя бы одного из элементов типа «Замыкание» приводит к отказу всей системы. В табл.1 представлены состояния системы из двух последовательно соединенных элементов с тремя состояниями и приведены выражения для расчета вероятностей этих состояний. Т а б л и ц а 1 - Таблица состояний последовательной системы
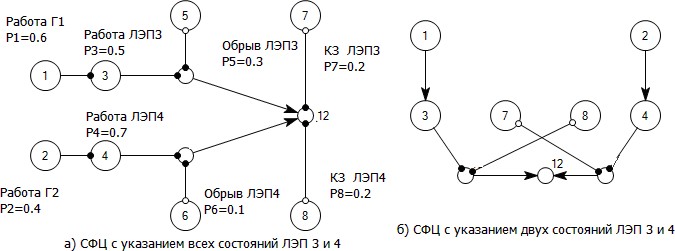
В табл.1 использованы следующие сокращения и обозначения: N, S, О – состояния работоспособности, отказа типа «Замыкание» или типа «Обрыв» - соответственно; 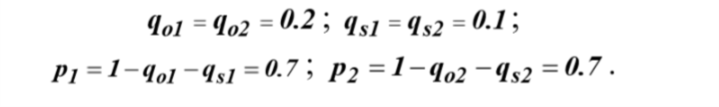 В табл.1 состояния 1-3 системы относятся к работоспособным, следовательно, вероятность безотказной работы системы В табл.1 состояния 1-3 системы относятся к работоспособным, следовательно, вероятность безотказной работы системы
 аналитическая часть выражения (2) может быть преобразована следующим образом 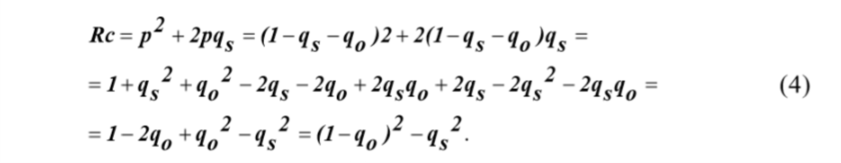 На основе выражения (4) можно доказать, что вероятность безотказной работы системы из n- последовательно соединенных элементов равна 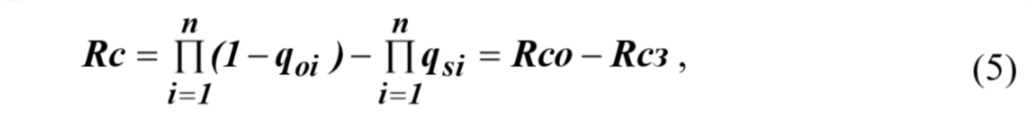 где Rco – безотказность по «обрыву»; Qcз – вероятность отказа системы из-за «замыкания». Выражение (5) приведен и представлено формулой в работе профессора И.А.Рябинина со следующим полезным в дальнейшем определением: «Надежность системы с последовательным соединением есть вероятность того, что система не откажет из-за отказов элементов типа «Обрыв», минус вероятность того, что система откажет из-за отказов элементов типа «Замыкание». Можно показать, что для параллельного соединения элементов формула (5) также справедлива. Кроме того, и для других, более сложных структур формула (5) может быть применена, если модель отказа участков с последовательным или параллельным соединением соответствует описанной выше. Схемы с учетом отказов элементов двух типов – типа «Обрыв» и типа «Замыкание»: 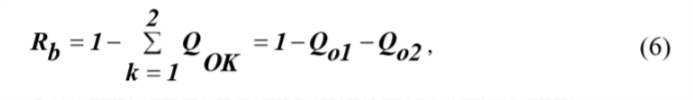 где Qo1 , Qo2 – вероятности появления системного отказа типа «Обрыв» (k=1) и типа «Замыкание» (k=2). Вероятности Qo1 и Qo2 рассчитываются путем подстановки в выражение для вероятности безотказной работы системы соответственно вероятностей отказов элементов типа «Обрыв» ( qоi ) и «Замыкание» ( qsi ). Например, для вероятности отказа системы из-за отказов типа «Замыкание» в приводится следующее выражение для вероятностной функции (ВФ). 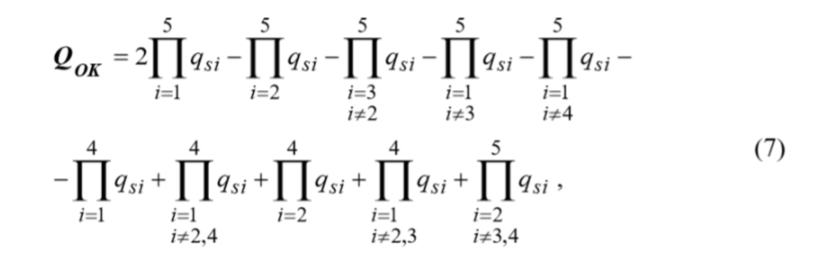 Полученное с использованием формулы вероятности суммы совместных событий, часто называемой иностранными авторами формулой “включения-выключения» (IE) или формулой Пуанкаре.. Следовательно, так как функция работоспособности системы (ФРС) состоит из параллельных кратчайших путей успешного функционирования (КПУФ), а каждый КПУФ есть последовательное соединение элементов, то формула (5) может быть применена к любой монотонной структуре (последовательной, параллельной, мостиковой и др.) с указанной выше моделью влияния вида отказов элементов на состояние системы. 2 Решение задач на ПК АРБИТР. Первая модель. Основной особенностью анализа надежности систем элементов с тремя состояниями является учет несовместности событий отказов элементов типа «Замыкание» и «Обрыв» . Перепишем уравнение (5) в следующем виде 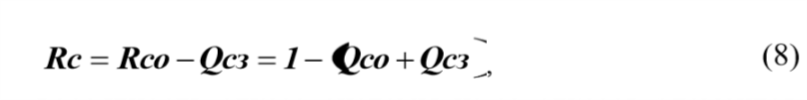 где Qco – вероятность отказа системы из-за отказов элементов типа «Обрыв». Правая часть выражения (8) соответствует вероятности события, логическая функция которого представлена конъюнкцией отрицаний двух несовместных событий [3, c.51]. Событиями являются отказы системы по причине «обрыва» и «замыкания». Доказательство этого свойства ГНС приведено в Приложении 1. Для решения поставленной задачи в ПК АРБИТР используется аппарат групп несовместных событий (ГНС) общего логико- вероятностного метода (ОЛВМ) [3,5], который может быть применен не только к отдельным событиям, но и к событиям, объединенным в эквивалентированные схемы. Методика решения на ПК АРБИТР включает в себя следующие этапы. Построение эквивалентированной схемы №1 для оценки вероятности отказа системы по «обрыву».Структура схемы совпадает со структурой заданной системы, а в качестве исходных данных используются вероятности безотказной работы элементов с учетом только отказов типа «обрыв», то есть 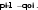 Построение эквивалентированной схемы №2 для оценки вероятности отказа системы по «замыканию».Структура схемы совпадает со структурой заданной системы, а в качестве исходных данных используются вероятности отказов элементов типа «замыкание» ( qsi). Эквивалентированные схемы соединяются как конъюнкция отрицаний двух несовместных событийНа рис.1-3 представлены фрагменты экранного интерфейса и схемы функциональной целостности (СФЦ), соответствующие указанным выше этапам решения задачи для случая последовательного соединения элементов с исходными данными, приведенными в табл.1. Этап 1. 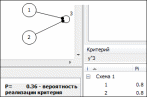 Рисунок 1 - Построение СФЦ для оценки вероятности отказа системы по «обрыву». На рис.1 показан фрагмент экранного интерфейса с СФЦ для расчета вероятности отказа последовательной системы. Согласно принятой модели влияния отказов элементов типа «обрыв» отказ системы (критерий y"3 ) происходит при отказе либо первого, либо второго элемента. Этап2. 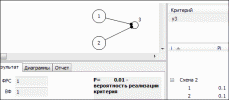 Рисунок 2 - Построение СФЦ для оценки вероятности отказа . На рис.2показан фрагмент экранного интерфейса с СФЦ для расчета вероятности отказа последовательной системы. Согласно принятой модели влияния отказов элементов типа «замыкания» отказ системы (критерий y3 ) происходит при отказе и первого, и второго элемента. Данный результат соответствует вероятности состояния 9 табл.1. Этап 3. 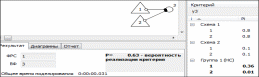 Рисунок 3 - Соединение эквивалентированных схем. На рис.3 показан фрагмент экранного интерфейса с СФЦ соединения эквивалентированных схем (на рисунке – треугольники) в форме конъюнкции несовместных событий 1 и 2 (критерий y3 ). Формирование группы 1 несовместных событий (НС) позволяет вычислить вероятность безотказной работы по формуле (8). В нашем случае вероятностная функция | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rc P1P3Q8 P2 P4Q7 - P1 P3Q8 | (9) |
В соответствии с правилами вычисления вероятностей произведений двух или более несовместных событий [3, c.50-51] при учете ГНС (события 3,5,7 и 4,6,8) имеем
 P3 Q7 P3 , . P3 Q7 P3 , .Q8 P4 P4. | (10) |
| Rc P1P3Q8 P2 P4Q7- P1 P3 P2P4 0.38. | (11) |
Для сравнения вероятность безотказной работы данной системы без учета ГНС
| | (12) |
Как видно из сравнения выражений (11) и (12) для данной модели влияния отказов элементов на отказы системы учет несовместности отказов типа «обрыв» и «замыкание» приводит к уменьшению численного значения вероятности безотказной работы системы.
Для подтверждения корректности полученных численных значений .
Заключение
На основе развития классических ЛВМ разработаны методики решения задач по оценки надежности систем, состоящих из элементов с тремя состояниями, с использованием ПК АРБИТР. Теоретической основой методики является реализованный в ПК АРБИТР аппарат групп несовместных событий [3,5-7]. Таким образом, показано, что логико-вероятностный подход позволяет решать задачи для тех случаев, когда число состояний элементовбольше двух, причем изменения состояний элементов являются стохастически зависимыми событиями.
Список использованных источников
Диллон Б., Сингх Ч. Инженерные методы обеспечения надежности систем. М.: Мир, 1984.
Рябинин И.А. Надежность и безопасность структурно-сложных систем. СПбГУ,
2007.
Черкесов Г.Н., Можаев А.С. Логико-вероятностные методы расчета надежности
структурно-сложных систем. М.: Знание, 1991.
Нозик А.А. Оценка надежности и безопасности структурно-сложных технических систем. Автореферат диссертации на соискание ученой степени кандидата технических наук. С-Петербург, 2005.
Поленин В.И., Рябинин И.А., Свирин С.К., Гладкова И.А. Применение общего логико-вероятностного метода для анализа технических, военных организационно- функциональных систем и вооруженного противоборства/ Под научным редактированием Можаева А.С. СПб.: NIKA, 2011.
Shannon C. “A Symbolic Analysis of Relay and Switching Circuits,” Transactions of the American Institute of Electrical Engineers, 57 (1938), 713-723.