отчет. Отчёт.НИР. 1 Описание способов обработки экспериментальных данных
 Скачать 178.46 Kb. Скачать 178.46 Kb.
|
 Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Комсомольский-на-Амуре государственный университет» Факультет энергетики, транспорта и морских технологий Кафедра «Тепловые энергетические установки» Научно-исследовательская работа Способы обработки экспериментальных данных Студенты группы 6ТЭб-1 А.Е. Григорьев Руководитель практики В.И. Шаломов 2020 Содержание 1 Описание способов обработки экспериментальных данных……….….......….3 2 Построение полученных результатов в графической форме ……..............…..7 Список использованных источников.....................................................................12 1 Описание способов обработки экспериментальных данных Регрессионный анализ является одним из основных методов в эконометрике. Его суть заключается в выявлении зависимости между различными явлениями и показателями. Обычно такие зависимости являются статическими. Их особенность заключается в том, что закономерность событий и явлений проявляются лишь в массе наблюдений. Кроме того, статические связи помимо основной математической составляющей учитывают и случайную составляющую, которая оказывает значительное влияние на уровень явления и показателя. Статические связи заключаются в том, что при изменении значения факторного признака меняются распределение результативного признака, т.е. разным значениям переменной x соответствуют разные распределения переменной y (y – результативный признак, x – факторный). Корреляционный и регрессивный анализ являются статическими методами, подробно изучаемые в эконометрике. Корреляционная связь – частный случай статической связи, при котором разным значениям переменной x соответствуют разные средние значения переменной y. Корреляционную связь можно определять, как между количественными, так и между качественными показателями. Изучение связи между количественными показателями называются регрессионными анализом. Если изучается связь между двумя переменными, одну из которых можно рассматривать как x, а другую – как y, то такой анализ называют парным регрессионным. В ходе проведения регрессионного анализа подбирают математическую функцию 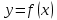 , которая наиболее лучшим образом соответствует исходным данным, т.е. обеспечивает наилучшую аппроксимацию поля корреляции. Поле корреляции – график, изображающий зависимость между x и y. По его форме можно судить о том, какая математическая зависимость больше подходит к исходным данным. , которая наиболее лучшим образом соответствует исходным данным, т.е. обеспечивает наилучшую аппроксимацию поля корреляции. Поле корреляции – график, изображающий зависимость между x и y. По его форме можно судить о том, какая математическая зависимость больше подходит к исходным данным.Линейная регрессия – используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости. Модель линейной регрессии является часто используемой и наиболее изучаемой в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели. Нелинейная регрессия − это вид регрессионного анализа, в котором экспериментальные данные моделируются функцией, являющейся нелинейной комбинацией параметров модели и зависящей от одной и более независимых переменных. Данные аппроксимируются методом последовательных приближений. Виды регрессионных моделей В заметке представление числовых данных в виде таблиц и диаграмм для иллюстрации зависимости между переменными X и Y использовалась диаграмма разброса. На ней значения переменной X откладывались по горизонтальной оси, а значения переменной Y − по вертикальной. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рисунке 1. 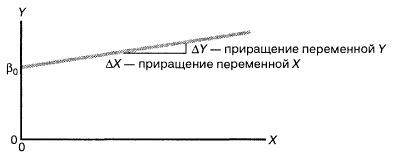 Рисунок 1 – Положительная линейная зависимость Простая линейная регрессия представляется в следующей форме: 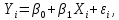 где 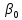 – сдвиг (длина отрезка, отсекаемого на координатной кривой Y); – сдвиг (длина отрезка, отсекаемого на координатной кривой Y);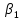 – наклон прямой Y; – наклон прямой Y;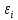 – случайная ошибка переменной Y в i-м наблюдении. – случайная ошибка переменной Y в i-м наблюдении.В этой модели наклон β1 представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной Y (положительного или отрицательного) на заданном отрезке оси X. Сдвиг 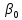 представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели εi является случайной ошибкой переменной Y в i-м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рисунке 2. представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели εi является случайной ошибкой переменной Y в i-м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рисунке 2. Рисунок 2 – Диаграммы разброса, иллюстрирующие разные зависимости На панели А значения переменной Y почти линейно возрастают с увеличением переменной X. Этот рисунок аналогичен рис. 1, иллюстрирующему положительную зависимость между размером магазина (в квадратных футах) и годовым объемом продаж. Панель Б является примером отрицательной линейной зависимости. Если переменная X возрастает, переменная Y в целом убывает. Примером этой зависимости является связь между стоимостью конкретного товара и объемом продаж. Напанели Впоказан набор данных, в котором переменные X и Y практически не зависят друг от друга. Каждому значению переменной X соответствуют как большие, так и малые значения переменной Y. Данные, приведенные на панели Г, демонстрируют криволинейную зависимость между переменными X и Y. Значения переменной Y возрастают при увеличении переменной X, однако скорость роста после определенных значений переменной X падает. Примером положительной криволинейной зависимости является связь между возрастом и стоимостью обслуживания автомобилей. По мере старения машины стоимость ее обслуживания сначала резко возрастает, однако после определенного уровня стабилизируется. Панель Д демонстрирует параболическую U-образную форму зависимости между переменными X и Y. По мере увеличения значений переменной X значения переменной Y сначала убывают, а затем возрастают. Примером такой зависимости является связь между количеством ошибок, совершенных за час работы, и количеством отработанных часов. Сначала работник осваивается и делает много ошибок, потом привыкает, и количество ошибок уменьшается, однако после определенного момента он начинает чувствовать усталость, и число ошибок увеличивается. На панели Е показана экспоненциальная зависимость между переменными X и Y. В этом случае переменная Y сначала очень быстро убывает при возрастании переменной X, однако скорость этого убывания постепенно падает. Например, стоимость автомобиля при перепродаже экспоненциально зависит от его возраста. Если перепродавать автомобиль в течение первого года, его цена резко падает, однако впоследствии ее падение постепенно замедляется. Мы кратко рассмотрели основные модели, которые позволяют формализовать зависимости между двумя переменными. Несмотря на то что диаграмма разброса чрезвычайно полезна при выборе математической модели зависимости, существуют более сложные и точные статистические процедуры, позволяющие описать отношения между переменными. В дальнейшем мы будем рассматривать лишь линейную зависимость. 2 Построение полученных результатов в графической форме 2 Построение полученных результатов в графической форме В таблице 1 представлены результаты экспресс-испытаний турбоагрегата ЛМЗ типа К-300-240. Таблица 1 – Сводная таблица экспресс - испытаний турбоагрегата ЛМЗ типа К-300-240
Продолжение таблицы 1
Продолжение таблицы 1
Продолжение таблицы 1
На основании полученных результатов (таблица 1) были построены графические зависимости. 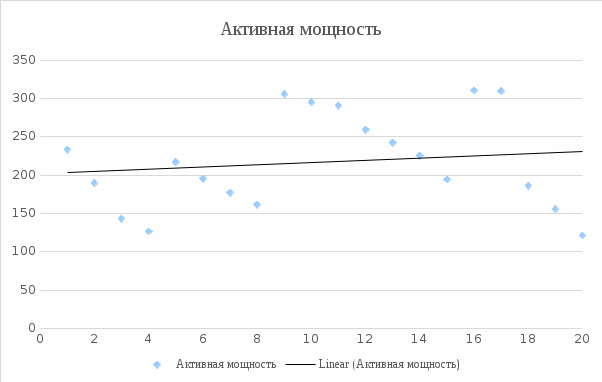 Рисунок 3 – График активной мощности 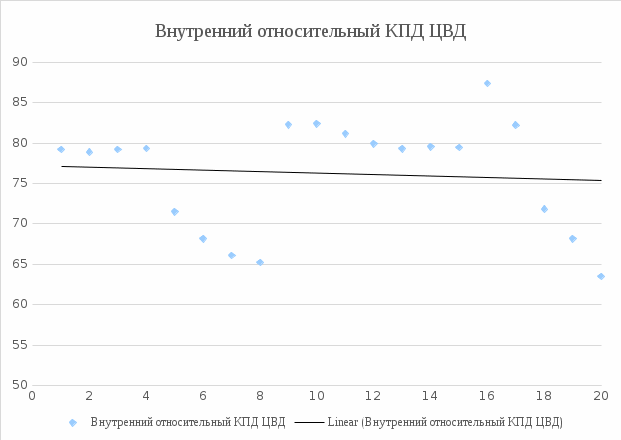 Рисунок 4 – График внутреннего относительного КПД ЦВД 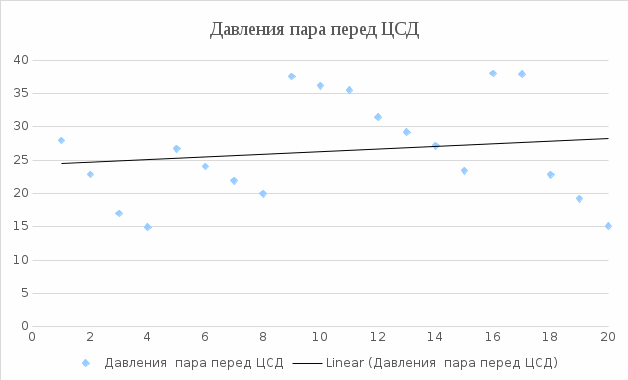 Рисунок 5 – График давлений пара перед ЦСД 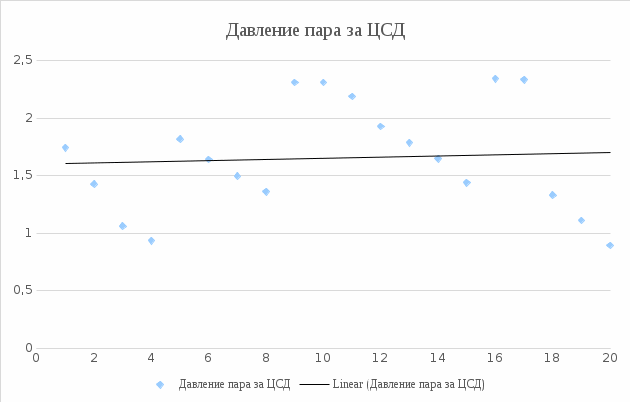 Рисунок 6 – График давления пара за ЦСД 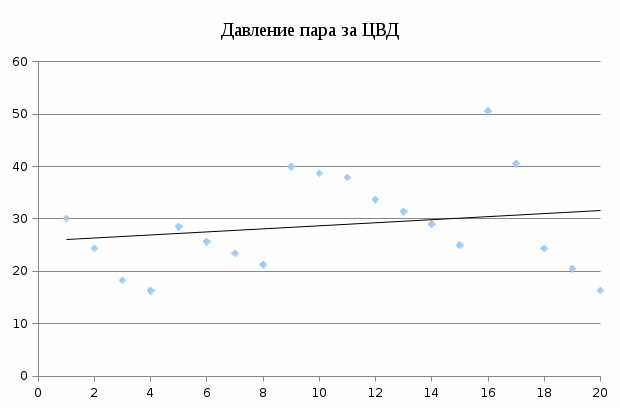 Рисунок 7 – Давление пара за ЦВД 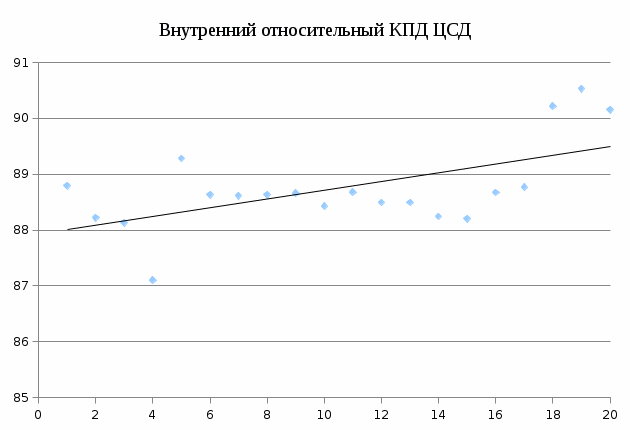 Рисунок 8 – Внутренний КПД ЦСД Список использованных источников 1 Плис, А. И. «Mathcad: математический практикум для экономистов и инженеров» / А.И. Плис, Н.А. Сивина. М. : Финансы и статистика, 1999. – 656 с. 2 Дьяков, В.П. Mathcad 7,0 в математике, физике и Internet / В.П. Дьяков, И.В. Абраменко. – М. : Нолидж, 1998. – 352 с. 3 MathCAD 6.0 PLUS.Финансовые, инженерные и научные расчеты в среде Windows 95. – М.: Информ. изд. Дом “Филинъ”, 1996. − 712 с. |

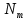 , МВт
, МВт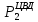 , кгс/см2
, кгс/см2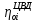 , %
, %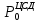 , кгс/см2
, кгс/см2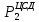 , кгс/см2
, кгс/см2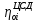 , %
, %