шПОРЫ И теория по матанализу. Шпоры и теория по матанализу. 1. Определение числовой функции. Способы задания функций
 Скачать 450 Kb.
|
|
31.  Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’(x)=   =  Найдите эластичность функции f (x) в точке x0: 38. f(x) = x4 , x0 = 9. Эластичностью функции y = f(x) в точке х0 называется предел  f (x) = x4 => E(x)=  , при x0 = 9.39. f(x) = 3x , x0 = 5. Эластичностью функции y = f(x) в точке х0 называется предел E(x)=  40. Докажите, что эластичность произведения двух функций равна сумме их эластичностей. Э   и  в точке  равна сумме эластичностей ф-ций в этой же точке:  . Эластичность равна Ey=x(lny)Д  тогда  .42. Сформулируйте теорему Ролля. Можно утвержд, что производная функции f(x) = (x-2)(x-3)(x-4)(x-5) обращается в нуль в трех точках интервала (2,5)? Пусть ф-ция  непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и  , то найдётся хотя бы одна точка  , в которой  .Можно. f(2)=0, f(3)=0, f(4)=0, f(5)=0 => существует С1из (2;3), такое, что f'(C1)=0, и тд 2, 3, 5, 4 43. Сформулируйте теорему Лагранжа. Докажите, что если f ′(x) = 0 на интервале (a,b), то функция f (x) постоянна на этом интервале. Пусть функция f(x) непрерывна на отрезке [a, b]; дифференцируема в интервале (a, b). Тогда существует точка с О (a, b) такая, что f(b) − f(a) = f '(c) · (b − a) 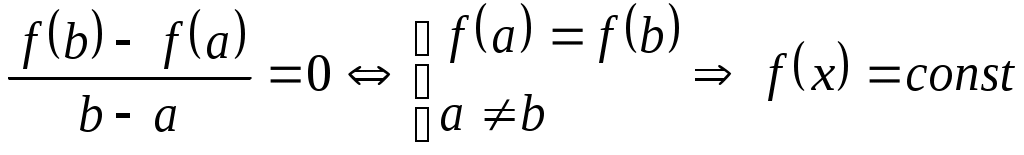 => 45. Сформулируйте теорему Коши для пары дифференцируемых функций. Выведите из теоремы Коши утверждение теоремы Лагранжа. Пусть функции f(x) и g(x) непрерывны на отрезке [a, b]; дифференцируемы в интервале (a, b); "x О (a, b) g'(x) ≠ 0 . Тогда существует точка c О (a, b) такая, что  .Частным случаем теоремы Коши (при g(x) = x) является теорема Лагранжа. 34. Сформулируйте и докажите теорему о производной произведения двух функций. Если 2 функции U и V дифференцированы в некоторой точке, то тогда ф-я, равная Y=U+V, также будет иметь производную, равную Y’=U’V+UV’ Док-во: Y=  =  Т.к. U(x0+x)= U + U = U(X0)+U, аналогично для V Раскрываем скобки и группируем  32. Следует ли из существования производной функции в точке ее непрерывность в этой точке? Если функция U=f(x) дифференцирована в некоторый точке x=x0, то она непрерывна в этой точке. Это условии необходимое, но недостаточное. Доказательство: пусть функция u= f(x) дифференцирована, тогда существует =а, тогда =а+(x), где (x) – б.м.Тогда y=xа + x(x), y = ( f ’(x0) x +x) = 0 в силу непрерывности. №46 Дайте определение многочлена Тейлора ф-ции f(x) в точке x0. Чему равны его производные в этой точке? Укажите какой-либо многочлен P(x), удовлетворяющий условиям:  .Пусть ф-ция f(x) имеет n производных в точке x0. Многочлен  называется n-многочленом Тейлора ф-ции f(x) в точке x0.Найдем производные:   аналогично  таким образом, для любого n, от 1 до к, выполняется равенство:  41. признак монотонности дифференцируемой функции: Промежутки монотонности ф-ции совпадают с промежутками постоянного знака её производной 42. определение локального экстремума функции одной переменной: Точка x0 называется точкой локального max [min] ф-ции f(x), если для всех x из некоторой окрестности точки x0 выполняется неравенство  Локальный max и min объединяются общим названием локальны экстремум. 43. необходимое условие локального экстремума функции одной переменной: Для того, чтобы дифференцируемая ф-ция f(x) имела в точке x0 локальный экстремум необходимо, чтобы в этой точке выполнялось равенство  . Если  при переходе через точку х0 меняет знак с + на – (с – на +), то х0 – это локальный максимум (минимум).. 44. точка перегиба функции: пусть функция f(x) непрерывна в точке х0. Точка х0 называется точкой перегиба, если при переходе через нее кривая меняет направление выпуклости . 45. необходимое условие точки перегиба: пусть функция f(x) непрерывна в точке х0. Точка х0 называется точкой перегиба, если при переходе через нее кривая меняет направление выпуклости ( слева и справа от х0 знаки второй производной различны) 46. определение асимптот графика функций: Асимптота графика функций y=f(x) - это прямая, расстояние до которой от точки (x,y) графика функций y=f(x) стремится к нулю, если хотя бы одна из координат (x,y) стремится к бесконечности. Асимптоты бывают вертикальными, наклонными и горизонтальными. 47. определение первообразной для функций y=f(x) на промежутке X: Пусть задана функция f(x) на интервале (a,b) . функция F(x) называется первообразной для функции f(x) на интервале (a,b), если F`(x)= f(x)для всех x принадлежащих (a,b). 48. определение неопределенного интеграла: Совокупность всех первообразных функций f(x) называется неопределенным интегралом и обозначается (« интеграл эф от икс дэ икс»). 49. свойства неопределенного интеграла:    51.Формула замены переменной в неопределенном интеграле. Если интеграл нельзя найти непосредственно, то в некоторых случаях можно применить метод замены переменной, положив х=ф(t), где ф(t)- непрерывно дифференцируемая монотонная функция. Справедливая формула замены переменной:  52.Формула интегрирования по частям для неопределенного интеграла. Пусть u(x) и v(x) – две дифференцируемые функции на промежутке Х. Тогда на Х выполняется формула интегрирования по частям  53.Определение определенного интеграла Римана. Если функция y=f(x) интегрируема на отрезке [a;b], то единственное число, разделяющее эти два множества называют определенным интегралом функции y=f(x) по отрезку[a;b] и обозначают следующим образом:  54. Достаточное условие интегрируемости. Функция y=f(x) называется интегрируемой на этом отрезке, если существует единственное число I, разделяющее множества нижних и верхних сумм Дарбу для всевозможных разбиений отрезка [a;b]. 56.Свойства определенного интеграла. 1)  . 2) 3)  4) ,для любых a,b,c. 5)Если f(x)≤g(x) отрезке [a,b], то  6)Если на отрезки [a,b] выполняется неравенства   (оценка интеграла). 7)Теорема о среднем. Для непрерывной на отрезке[a,b] функция y=f(x) найдется точка С принадлежащая [a,b],что .57.Формула Ньютона-Лейбница. Для нахождения определенного интеграла для функции f(x), интегрируемой на отрезке[a,b]:  , гдеF(x)- любая первообразная для функции f(x) на[a,b]. 58.Формула замены переменной в определенном интеграле. Пусть в определенном интеграле  с непрерывной подынтегральной функцией f(x) производят замену переменной x= (t), при чем функция (t) непрерывно дифференцируема на отрезке [ ] и  тогда справедливо равенство (t)dt. 59.Формула интегрирование по частям для определенного интеграла. Пусть u(x) и v(x)-две непрерывно дифференцируемые функции на отрезке [a,b]. Тогда выполняется формула интегрирования по частям  │ 60. Определение несобственного интеграла с бесконечно верхним пределом.   Если существует конечный предел  , тоэтот предел называется несобственным интегралом с бесконечно верхним пределом пределом от функции f(x)и обозначается  .61.Определение несобственного интеграла с бесконечно нижним пределом. Еслисуществует конечный предел  , то этот предел называется несобственным интегралом с бесконечно нижним пределом от функции f(x) и обозначается .62.Определение несобственного интеграла от неограниченной функции на ограниченном промежутке. Если функция f(x) определена при  , интегрируема на любом отрезке и не ограничена слева от точки b, то по определению полагают Аналогично, если функция f(x) не ограничена справа от точки а, то . Наконец, если функция в окрестности внутренней точки с отрезка [a,b]не ограничена, то по определению .74. Докажите, что если F1(x) и F2 (x) - первообразные функции f (x) на интервале X , то F2 (x) = F1(x) + C , где C - некоторая постоянная. |