шПОРЫ И теория по матанализу. Шпоры и теория по матанализу. 1. Определение числовой функции. Способы задания функций
 Скачать 450 Kb. Скачать 450 Kb.
|
|
Функция y = f (x) называется непрерывной в точке х = х0 , если эта функция определена в какой-либо окрестности точки х0 и в самой точке х0 , и если бесконечно малому изменению аргумента соответствует бесконечно малое изменение функции. 23.Теорема о непрерывности сложной ф-ции. Сложная функция, составленная из конечного числа суперпозиций непрерывных функций, тоже непрерывная функция. 24. Теорема о непрерывности обратной ф-ции. Функция обратная для монотонной и непрерывной функции также непрерывна. 25. Теорема о непрерывности элементарных ф-ций. Любая элементарная функция непрерывна в своей области определения. (Промежутки непрерывности элементарных функций точно совпадают с их областью определения). 26. Точка х0 называется точкой разрыва функции f(x), если Разрыв 1 рода (скачок) если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы. Разрыв 2 рода (бесконечный), если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен. Разрыв 3 рода (устранимый), если функция не существует в точке х0 или если значение функции в точке х0 не совпадает со значением односторонних пределов. 27.определение производной в точке Пусть функция 28. Если функция y = f(x) имеет производную в точке х0 , то мы говорим, что функция дифференцируема в этой точке. 29. Дифференциалом функции в точке х0 называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению. df(х0)= f ′ (х0) ∆х; ∆х=dх; df(х0)= f ′ (х0) dх 30. Общие правила дифференцирования. ( f (g (x)) )’ = f ‘(g(x)) · g ‘ (x) (u v )’ = v · u v-1 · u’ + uv · v’ · ln u 31.Теорема о производной обратной функции. Если функция y=f(x) имеет обратную функцию x=g(y) и в точке х0 производная f(x) не равна нулю, то обратная функция g(y) диффернцируема в точке у0=f(x0) и g(y0)=1/f(x0) или xy=1/yx. 32.Теорема о производной сложной функции. .Если функция у=f(x) дифференцируема в точке t0 и g(t0)=x0, то сложная функция y=f(g(x)) также дифференцируема в t0 и выполняется следующая формула: d f(g(t))/dt|t=to=f(x0)*g(t0) или yt=yx*xt. 33. Геометрический смысл производной и дифференциала. Приращением функции y =f(x) в точке x0 называется разность Δу=f(x)-f(x0)= f(x+Δx)-f(x0) Производной от функции y=f(x) в точке х0 наз. Предел отношения Δу/Δх, когда Δх→0 (при усл., что этот предел существует) Написать обозначение производной. Геометрический смысл производной. Пусть Г- график функции y=f(x). Рассмотрим на Г т. А(x0,f(x0)) и т. В (x0+Δx,f(x0+Δx)) Прямая АВ называется секущей. Будем считать, что y=f(x)-непрерывная функция, тогда если Δх→0, то f(x0+Δx)→f(x0), т.е. В→А при Δх→0. Пусть γ – угол наклона секущей относительно оси ОХ. Если существует предел lim γ=γ0 при Δх→0, то прямая, проходящая через А и образующая с осью ОХ угол γ0, называется касательной к Г в точке А. Пусть С(f(x0+Δх), f(x0)) – точка, дополняющая отрезок АВ до прямоуг. треугольника АВС. Т.к. АС//ОХ, то tgγ =Δу/Δх. Переходя к пределу, получим: tgγ0=f′(x0) Т.е. геометрический смысл производной состоит в том, что f′(x0) – это тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x0)). 34. Уравнение касательной. Найдем ур-е касательной к графику Г ф-и y=f(x) в точке А(х0, f(x0)): т.к. т. А принадлежит Г и ур-ю касательной, то f(x0)=kx0+b, откуда b= f(x0)-kx0, значит, касательная задается след. Ур-м: y= kx+ f(x0)-kx0= f(x0)+k(х-x0) Т.к. k= f′(x0), то y=f(x0)+ f′(x0)(х-х0). 34. Определение эластичности функции. функции y = f(x) в точке х0 называется следующий предел Eyx(x0) = lim ((Δy/y): (Δx/x)). Δx 0 Эластичность Ey – это коэффициент пропорциональности между относительными изменениями величин y и x.) 35. Теорема Ролля. Если функция, непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю. 36. Теорема Лагранжа. Пусть функция f(x) непрерывна на отрезке [a, b]; дифференцируема в интервале (a, b). Тогда существует точка с О (a, b) такая, что
Формула (1) называется формулой Лагранжа, или формулой конечных приращений 37. Теорема Коши. Пусть даны две функции f(x) и g(x)такие, что: f(x) и g(x)определены и непрерывны на отрезке производные производные тогда (Если убрать условие 4, то необоходимо усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале (a,b).) 38. Правило Лопиталя. Теорема (правило Лопиталя). Пусть А – число, символ одностороннего предела (А=а±0) или символ бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно малые, либо обе бесконечно большие при х→А. Тогда, если существует предел ( то существует и предел при этом выполняется равенство: 39. Производные и дифференциалы высших порядков. Если для функции y=f(x) определена производная у(к-1) порядка (к-1), то производную у(к) порядка к (при условии ее существования) определяют как производную от производной порядка (к-1), т.е. у(к) = (у(к-1))′ . В частности, у’’=(y’)’- производная второго порядка, y’’’=(y’’)’ – третьего и т.д. Дифференциалы высших порядков ф-и y=f(v) последовательно определяются таким образом: d2y=d(dy) – диф-л 2-го порядка d3y=d(d2y)… dny=d(d n-1 y) - диф-л n-го порядка 40. Формула Тейлора. Формула Маклорена. теорема Тейлора. Пусть функция f(x) имеет в точке x = a и некоторой ее окрестности производные порядка n+1. Тогда между точками a и x a найдется такая точка
Формула (10) называется формулой Тейлора, а выражение представляет остаточный член в форме Лагранжа. Заметим, что если функция f(n+1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a)n. Таким образом, остаточный член можно записать в виде Rn+1(x) = o((x-a)n)при x a. Данная форма записи остаточного члена называется формой Пеано. Формулой Маклорена называется формула Тейлора при a = 0:
Остаточный член в форме Пеано для формулы Маклорена имеет вид Rn+1 = o(xn) при x 0. П 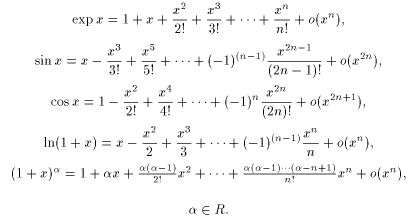 риведем разложения некоторых элементарных функций по формуле Маклорена риведем разложения некоторых элементарных функций по формуле Маклорена Найдите, исходя из определения, производную функции f(x) в точке x0: 26. f(x) = x3, x0 - произвольное число. Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’(x)= f(x) = x3 f ′(xо)= 27. f(x)=sinx, xо-произвольное число Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’(x)= f ′(xо)= 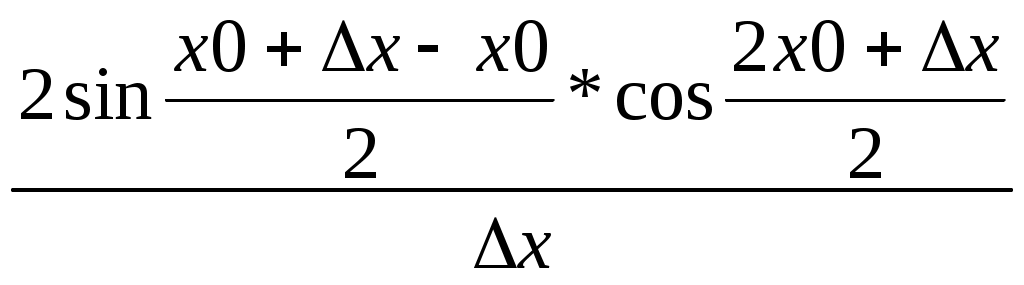 =cosx0 =cosx028. f(x)= Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’(x)= f ’(x)= 29. f(x)= Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’(x)= f ’(x)= 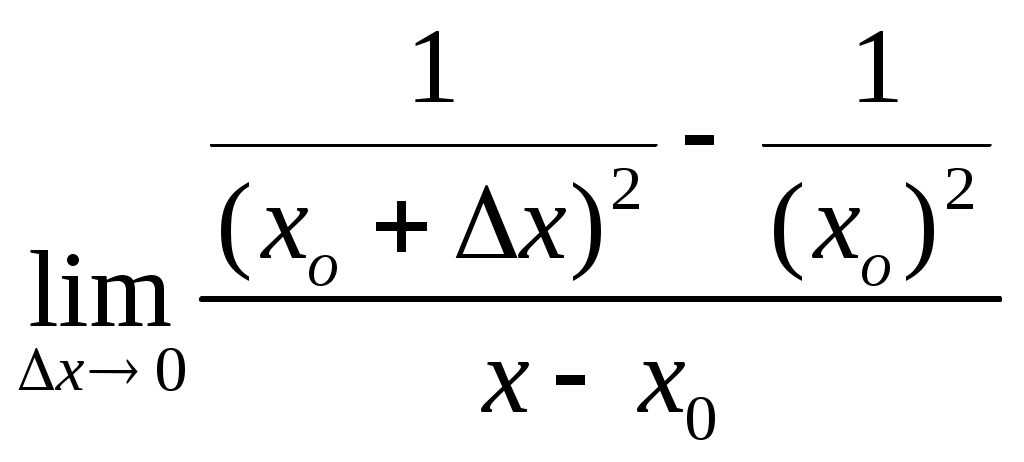 = =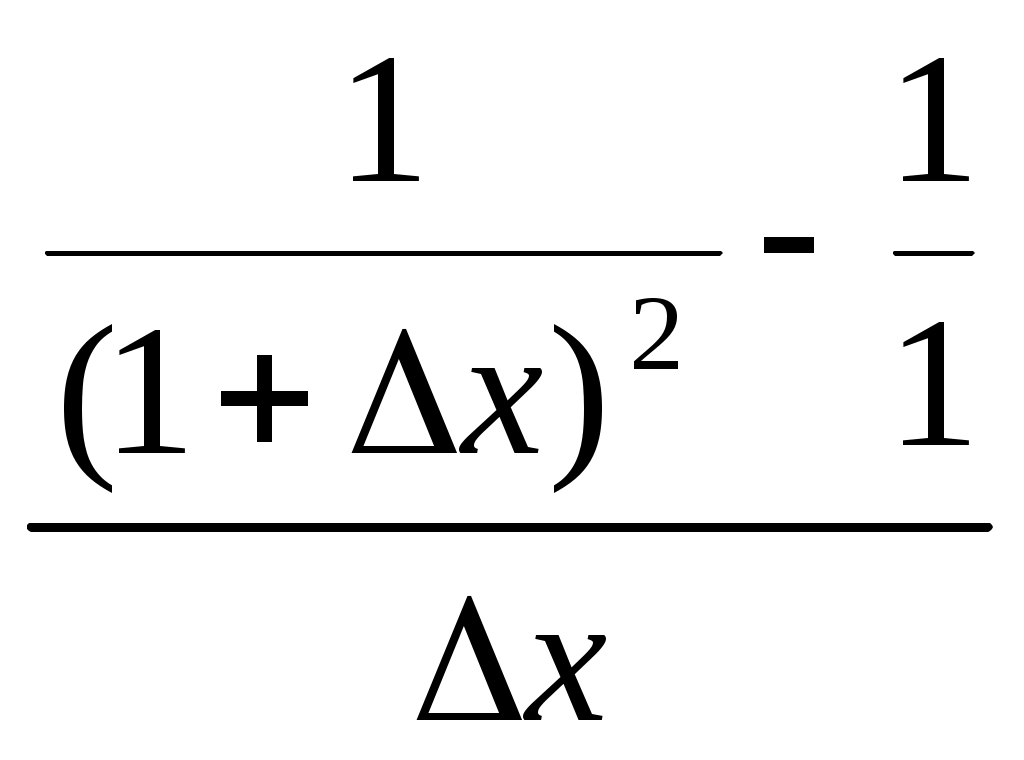 = =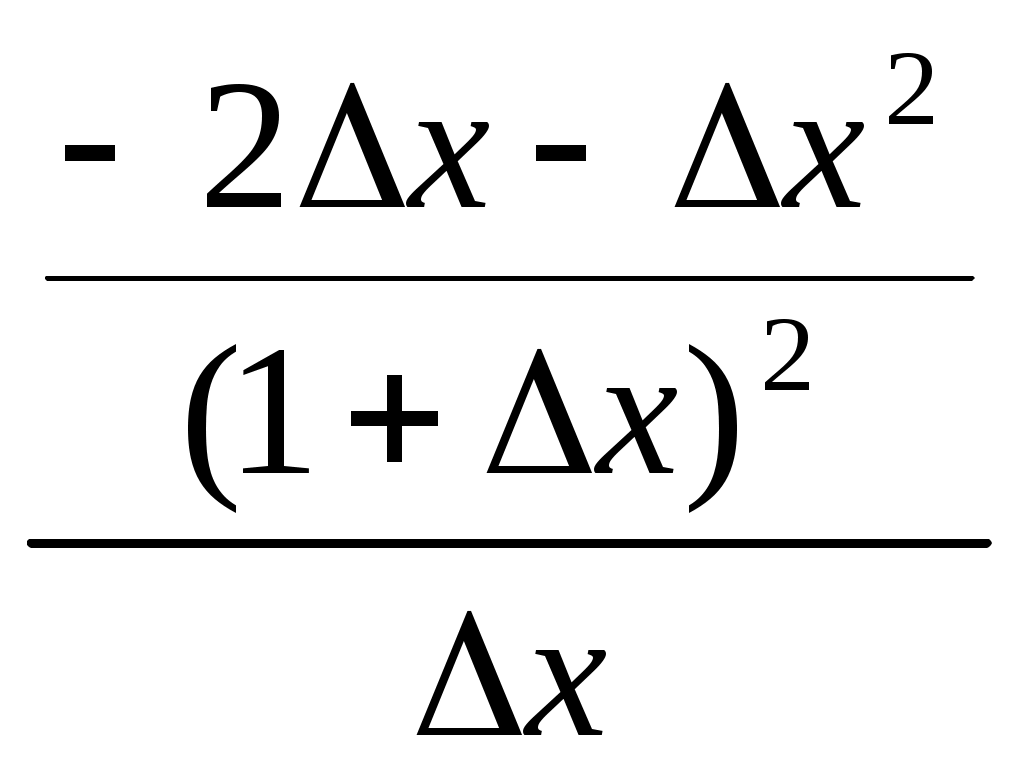 =-2 =-230. f(x)=xx, x0=0 Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0. f ’(x)= |
