Основы программирования лабороторная работа 1. 1. Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа

• Название: 1. Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа
• Дата: 05.11.2022
• Размер: 104.91 Kb.
• Имя файла: Основы программирования лабороторная работа 1.docx
• Тип: Документы; #771360

1. Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа.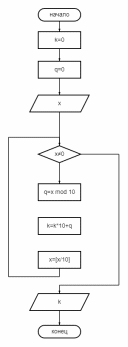



Тестовая таблица

x	k	Примечания
1234	4321	q=4 k=4 x=123 q=3 k=43 x=12 q=2 k=432 x=1 q=1 k=4321 x=0 Вывод: 4321
100	1	q=0 k=0 x=10 q=0 k=0 x=1 q=1 k=1 x=0 Вывод: 1

2. Даны натуральное n и вещественные числа x1, y1, x2, y2, … xn, yn. Рассматривая пары xi,yi как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки.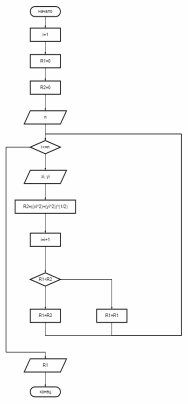 

n	xi	yi	Примечания
3	4,3,7	2,1,1	i=1 R2=√20 R1=√20 i=2 R2=√10 R1=√20 i=3 R2=√50 R1=√50 Вывод: √50
4	-5,2,8,3	1,-2,-4,0	i=1 R2=√26 R1=√26 i=2 R2=2 R1=√26 i=3 R2=√80 R1=√80 i=4 R2=3 R1=√80 Вывод: √80

Тестовая таблица

3. Известно, что из четырех чисел a1, a2, a3, и a4 одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n.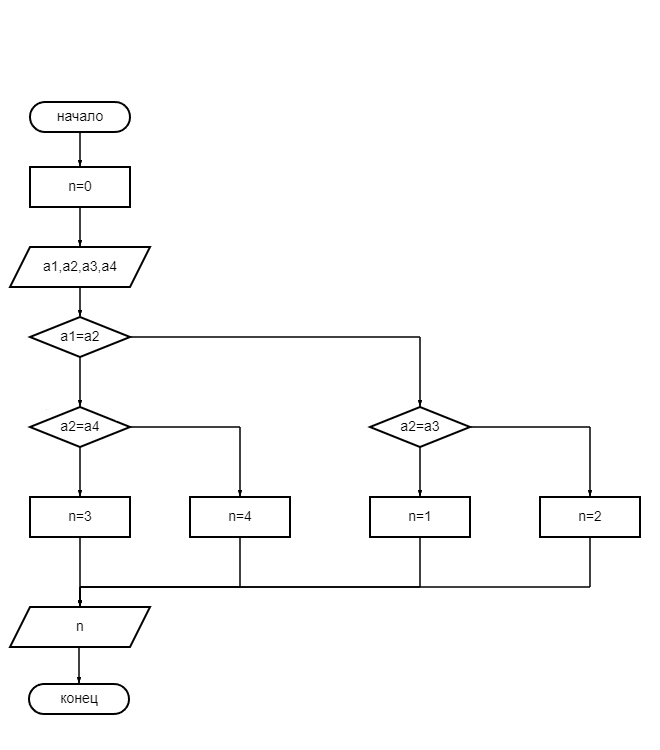

a1	a2	a3	a4	Примечания
2	2	2	6	a1=a2 a2≠a4 Вывод: 4
7	1	7	7	a1≠a2 a2≠a3 Вывод: 2
8	8	99	8	a1=a2 a2=a4 Вывод: 3

Тестовая таблица

4.  Дана непустая последовательность положительных целых чисел, за которой следует 0 (это признак конца последовательности). Вычислить среднее арифметическое этих чисел.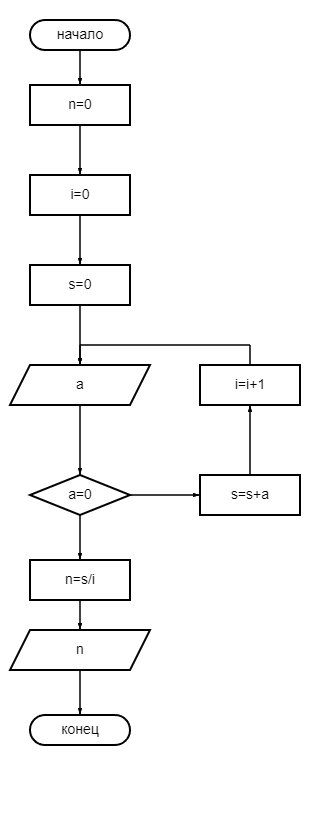 



Тестовая таблица

a	Примечания
1,8,4,10,0	s=1 i=1 s=9 i=2 s=13 i=3 s=23 i=4 n=23/4=5,75 Вывод: 5,75
2,14,0	s=2 i=1 s=16 i=2 n=16/2=8 Вывод: 8

5. Дана непустая последовательность ненулевых целых чисел, за которой следует 0 (это признак конца последовательности). Определить, сколько раз в этой последовательности меняется знак. (Например, в последовательности 1, -34, 8, 14, -5 знак меняется 3 раза). 

a	Примечания
7, -20, 412, -200, 0	a=b (7=7), b=7 a<0 (-20), b>0 (7), i=1, b=-20 a>0 (412), b<0 (-20), i=2, b=412 a<0 (-200), b>0 (412), i=3, b=-200 Вывод: 3
6, -1, 10, 20, 0	a=b (6=6), b=6 a<0 (-1), b>0 (6), i=1, b=-1 a>0 (10), b<0 (-1), i=2, b=10 a>0 (20), b>0 (10), i=2, b=20 Вывод: 2

Тестовая таблица

6. Дано 50 вещественных чисел. Определить, сколько из них больше своих «соседей», т.е. предыдущего и последующего чисел. 

Последовательность	i	k	Примечания
1,2; 2,013; 3,04; 4,4; 5,12; 4,09	7	1	Т.к в последовательности 7 чисел и i=7, то для 50 чисел будет верным условие i<51. В случае, если b=a и b=c, алгоритм будет работать. Последнее число в цикл входить не будет, т.к не будет числа спереди.

Тестовая таблица

7. Дана непустая последовательность положительных целых чисел, за которой следует 0 (это признак конца последовательности). Вычислить среднее геометрическое этих чисел. 

a	Примечания
5, 25, 1, 5, 0	a=5, s=5, i=1 a=25, s=125, i=2 a=1, s=125, i=3 a=5, s=625, i=4 Вывод: 5
2, 15, 3, 8, 0	a=2, s=2, i=1 a=15, s=30, i=2 a=3, s=90, i=3 a=8, s=720, i=4 Вывод: 5.180040

Тестовая таблица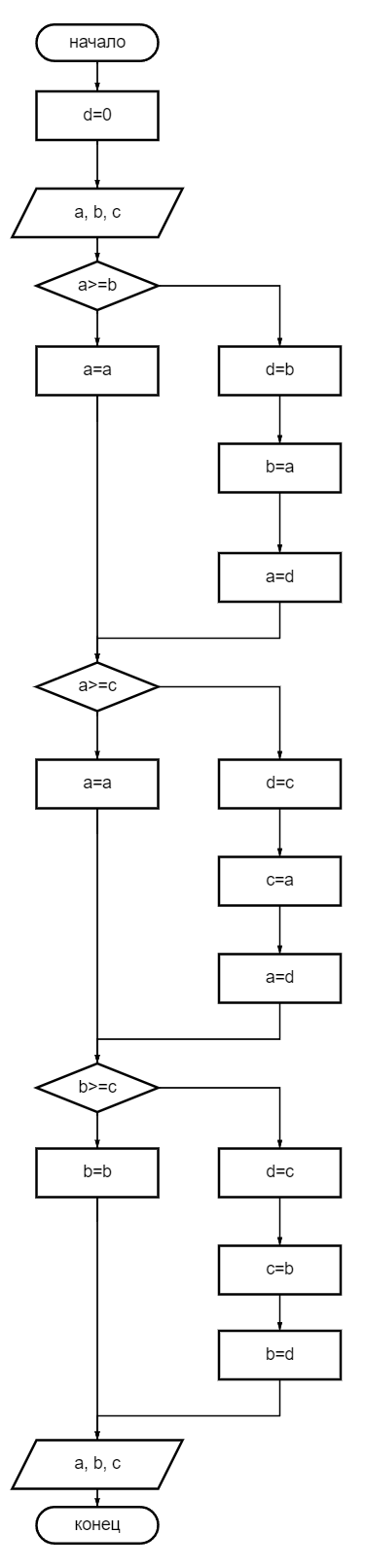

8.  Значения переменных a, b и c поменять местами так, чтобы оказалось a≥b≥c.

a	b	c	Примечания
1	32	94	a d=b=32, b=a=1, a=d=32 a d=c=94, c=a=32, a=d=94 b d=c=32, c=b=1, b=d=32 Вывод: 94, 32, 1
12	43	10	a d=b=43, b=a=12, a=d=43 a>c, поэтому a=a=43 b>c, поэтому b=b Вывод: 43, 12, 10

Тестовая таблица