Физика. 1. Определить потенциал поля, образованного диполем в точках плоскости, перпендикулярной его оси и проходящей через середину отрезка, соединяющего заряды диполя. Решение
 Скачать 109.78 Kb. Скачать 109.78 Kb.
|
|
1. Определить потенциал поля, образованного диполем в точках плоскости, перпендикулярной его оси и проходящей через середину отрезка, соединяющего заряды диполя. Решение: Электрический диполь - это электро-нейтральная система, состоящая из точечных и равных по абсолютной величине: положительного и отрицательного электрических зарядов q1 = - q2. 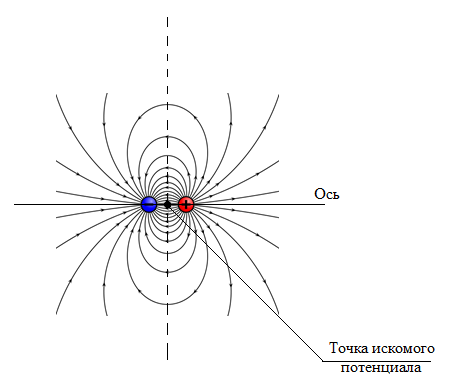 Потенциал φ зависит от величины заряда и расстояния от точки, где измеряется потенциал, до самого заряда: 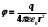 (1.1) (1.1)В нашем случае, поскольку перпендикуляр проходит через середину отрезка, соединяющего заряды, то расстояние от точки до каждого из зарядов одинаково: r1 = r2 Кроме того, потенциал φ, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов: 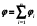 (1.2) (1.2)Таким образом, согласно формулам (1.1) и (1.2), а так же условиям q1 = -q2 и r1 = r2= r мы получим: 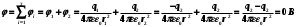 Ответ: φ = 0 В 2. Определить плотность тока, если за 2 с через проводник, сечением 1,6 мм2 прошло 2*1019 электронов (заряд электрона е = 1,6*10-19 Кл). Дано: t = 2 c. S = 1,6 мм2 N = 2∙1019 e = 1,6∙10-19 Кл Найти: J Решение: Зная заряд одного электрона и количество электронов, вычислим полный заряд, прошедший по проводнику: 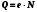 (2.1) (2.1)Плотность тока J — это векторная физическая величина, модуль которой определяется отношением силы тока I в проводнике к площади S поперечного сечения проводника, т.е: 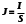 (2.2) (2.2)Сила тока — скалярная физическая величина, определяемая отношением заряда ΔQ, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, тогда в нашем случае: 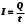 (2.3) (2.3)Подставляя (2.1) в (2.3), а затем (2.3) в (2.2) получим: 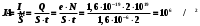 Ответ: J = 106 А/м2 3. На какую длину волны настроен колебательный контур, состоящий из конденсатора ёмкостью 445 пФ и катушки индуктивности L = 1 мГн ? Дано: C = 445 пФ = 445∙10-12 Ф L = 1 мГн = 0,001 Гн с = 300000 км/с = 3∙108 м/c Найти: 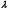 Решение: По формуле Томпсона период электромагнитных колебаний в контуре: 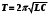 (3.1) (3.1)Длина волны, на которую настроен контур: 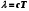 (3.2) (3.2)Примем скорость света равной c = 3∙108 м/c. Подставляя (3.1) в (3.2) получаем: 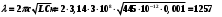 Ответ: 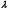 = 1257 м = 1257 м4. Обмотка соленоида имеет сопротивление 10 Ом. Какова его индуктивность, если прохождении тока за 0,05 с в нём выделится количество теплоты, эквивалентное энергии магнитного поля соленоида. Дано: R = 10 Ом t = 0,05 с. Найти: L Решение: Обозначим: W - энергия магнитного поля соленоида, Q - количество теплоты, выделяемое в обмотке соленоида за время t, I - конечное значение тока в обмотке соленоида. Тогда, энергия, запасенная в соленоиде: 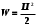 (4.1) (4.1)Если принять, по умолчанию, что ток в обмотке соленоида за всё время t не меняется и равен I, то согласно закону Джоуля –Ленца: 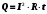 (4.2) (4.2)В этом случае, приравняв (4.1) и (4.2), получаем: 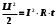 (4.3) (4.3)Откуда значение индуктивности находится как: 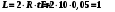 Ответ: L = 1 Гн 5. Площадь каждой обкладки плоского воздушного конденсатора 314 см2, расстояние между ними – 2 мм, напряжённость поля между обкладками 60 кВ/м. Какую работу надо совершить, чтобы вдвинуть между обкладками стеклянную пластину (ε = 7), если она полностью заполнит конденсатор и конденсатор после зарядки отключён от источника питания. Дано: S = 314 см2 = 0,0314 м2 d = 2 мм = 0,002 м E = 60 кВ/м = 60000 В/м ε2 = 7 ε1=1 ε0 = 8,85∙10-12 Ф/м Найти: A Решение: Для нахождения работы, которую потребуется совершить, нам необходимо найти разность энергий, запасенных в конденсаторе до внесения стеклянной пластины и после: 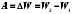 (5.1) (5.1)Отметим, что до внесения стеклянной пластины, в качестве диэлектрика между обкладками выступал воздух с диэлектрической проницаемостью εв=1. После внесения стеклянной пластины, она заполнила всё пространство между обкладками, и в качестве диэлектрика между обкладками стало выступать стекло с ε = 7. Энергия, запасенная в конденсаторе: 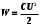 (5.2) (5.2)Причем, напряжение между обкладками и напряженность поля связаны соотношением: 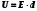 (5.3) (5.3)Заряд, который накапливается на обкладках конденсатора: 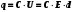 Поскольку конденсатор отключен от источника питания, то заряд остается не именным: q = const. Тогда получим:  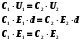 (5.4) (5.4)Откуда: 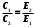 (5.5) (5.5)Емкость плоского конденсатора: 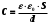 (5.6) (5.6)Поскольку величины ε0, S и d не могут измениться при внесении пластины, то соотношение емкостей до внесения пластины и после находится как соотношение значений диэлектрической постоянной: 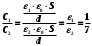 (5.7) (5.7)Используя соотношение (5.5) и (5.7) получаем: 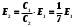 (5.8) (5.8)Заметим, что ε2 = 7ε1. Тогда, используя (5.2) - (5.8) и подставляя в (5.1) получим: 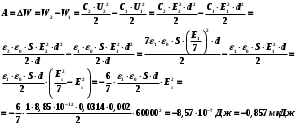 Ответ: А = -0,857 мкДж 6. Сила тока в проводнике равномерно возрастает от 0 до 5 А в течение 10 с. Определить заряд, прошедший по проводнику за это время. Дано: I0 = 0 А I = 5 A τ = 10 c. Найти: Q Решение: Силой тока называется физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени: 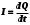 (6.1) (6.1)Откуда заряд находится как: 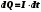 (6.2) (6.2)В нашем случае сила тока не постоянна и изменяется со временем по линейному закону. Тогда закон изменения силы тока можно записать в виде линейного уравнения: 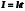 (6.3) (6.3)Где коэффициент k равен: 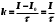 (6.4) (6.4)Подставим (6.3) в (6.2) и получим: 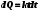 (6.5) (6.5)Вычислим интеграл: 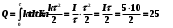 Ответ: Q = 25 Кл |
