ЛР 1 мэт. 1 Основные понятия и определения
 Скачать 59.59 Kb. Скачать 59.59 Kb.
|
|
Цели работы: измерение сопротивлений объемных и тонкопленочных резисторов; исследование зависимостей удельных электрических сопротивлений и их температурных коэффициентов от температуры и состава резистивных материалов, а также зависимостей термоЭДС термопар от разностей температур контактов. 1.1. Основные понятия и определения К основным электрическим характеристикам проводниковых материалов относят удельное сопротивление ρ и температурный коэффициент удельного сопротивления αρ. Наилучшими проводниками электрического тока являются металлы, механизм протекания тока в которых заключается в коллективном движении свободных электронов под действием приложенного электрического поля. Интенсивность рассеяния определяет среднюю длину свободного пробега электрона и, в конечном счете, значение удельного сопротивления проводника, которое может быть выражено следующим образом: где m – масса электрона; u – средняя скорость теплового движения; e – заряд электрона; n0 – концентрация свободных электронов; λ – средняя длина свободного пробега. Относительное изменение удельного сопротивления при изменении температуры на один кельвин называют температурным коэффициентом удельного сопротивления: Для многих двухкомпонентных сплавов значение остаточного сопротивления от состава хорошо описывается параболической зависимостью где xA, xB - атомные доли компонента в сплаве. В микроэлектронике широко применяются в качестве различных элементов схем тонкие металлические пленки. Для сравнительной оценки проводящих свойств пленки пользуются сопротивлением квадрата поверхности R0 = /d, где - удельное сопротивление слоя толщиной d. Термоэлемент, составленный из двух различных проводников, образующих замкнутую цепь, называют термопарой. Если цепь разорвать в произвольном месте, то на концах разомкнутой цепи появятся термоэлектродвижущая сила. В относительно небольшом температурном интервале термоЭДС пропорциональна разности температур контактов: U = T (t2 - t1). Описание установки Измерение сопротивления исследуемых проводников и термоЭДС термопар производится с помощью мультиметра, постоянно подключенного к испытательному стенду. Все исследуемые образцы расположены в корпусе стенда; резисторы R1, R2, R3 и один из спаев каждой из трех термопар помещены в общий термостат. Подключение образцов к измерительному прибору осуществляется нажатием соответствующей контактной кнопки на лицевой панели стенда. Маркировка кнопок соответствует маркировке образцов. Обработка результатов. 1.Расчет удельного сопротивления металлических проводников = Rπ(D/2)2/L где R - сопротивление образца; S - площадь поперечного сечения; l - длина проводника. 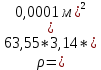
Расчет сопротивления квадрата поверхности металлических пленок R□ = Rb/L где R - сопротивление образца; b - ширина резистивного слоя; L - длина пленки. 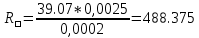
3. Расчет температурного коэффициента удельного сопротивления = R + l, Где R и l - температурные коэффициенты сопротивления и линейного расширения 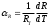 Значение производной dR/dt найти путем графического дифференцирования зависимости R(t) с помощью функции ЛИНЕЙН. Медь 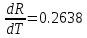 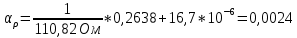 Никель 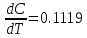 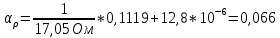 Константан 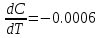 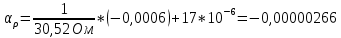
График зависимости сопротивлений исследуемых материалов от температуры: 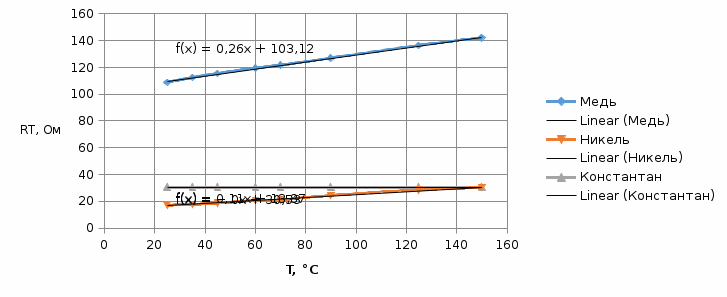 График зависимости температурного коэффициента удельного сопротивления исследуемых материалов от температуры: 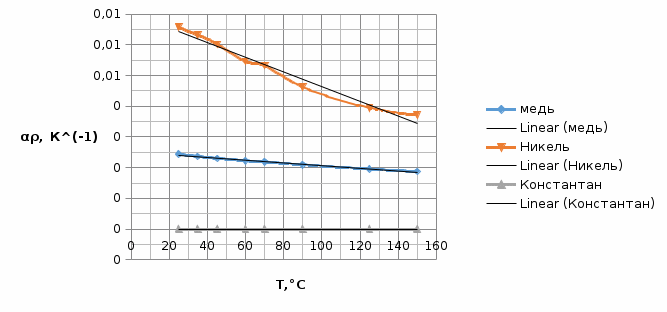 6. Расчет удельного сопротивления сплавов Cu-Ni Cu-Ni = NixNi + Cu(1 - xNi) + СxNi(1 - xNi) 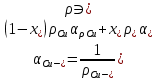 где xNi - содержание никеля в сплаве в относительных долях по массе. Коэффициент С находят путем подстановки значения удельного сопротивления константана и соответствующего ему содержания никеля 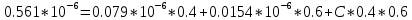 C=2.16 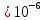 При xNi=0.2 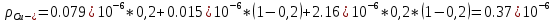 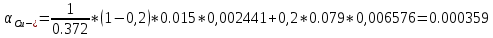
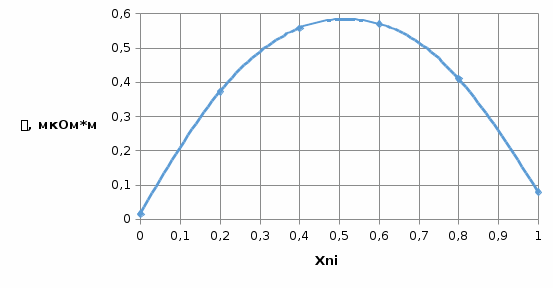 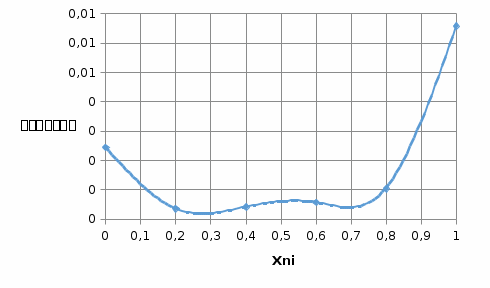 7. Зависимость ЭДС исследуемых термопар от температуры:
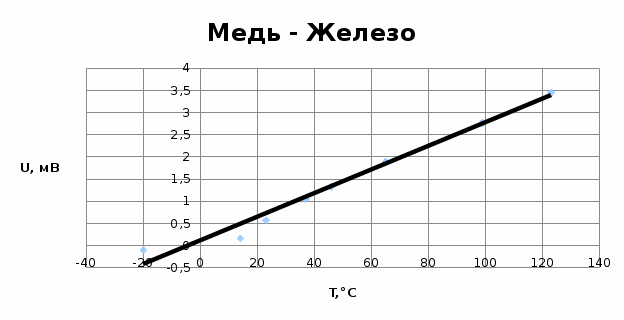 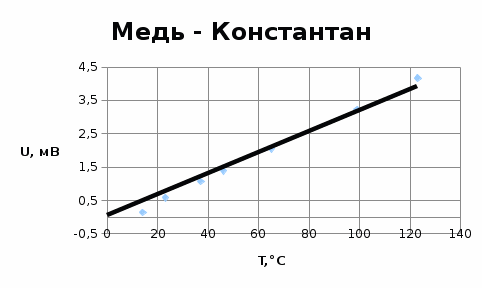 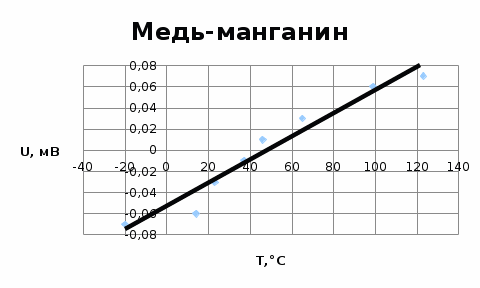 Вывод: на основании результатов проделанных мной экспериментов я рассчитал удельные сопротивления группы металлов (см. таблицу в п.1), полученные мной величины приблизительно равны табличным, что говорит о верности моих расчетов и правильности проведения экспериментов. При рассмотрении графиков п. 2-4 видно, что сопротивление меди и никеля растет вместе с температурой линейно. Это вызвано увеличением тепловых колебаний узлов кристаллической решетки. Константан является медно-никелевым сплавом (Cu около 59%, Ni 39-41%, Mn 1-2%), а для сплавов этого типа изменение проводимости дополнительно обуславливается возрастанием концентрации носителей заряда при повышении температуры. Контрольные вопросы 1. Почему металлы обладают высокой электрической проводимостью? Ответ: Потому что их электроны, которые находятся на последнем уровне очень слабо связаны с атомо. Они свободно могут перемещаться по всему объёму металла. 2. Чем обусловлено возрастание удельного сопротивления металлов при нагревании? Ответ: электронный газ в металлах находится в вырожденном состоянии. Поэтому концентрация электронов и их средняя энергия практически не зависят от температуры, но с повышением температуры увеличивается амплитуда колебаний атомов в узлах кристаллической решетки, что приводит к более интенсивному рассеянию электронов в процессе их направленного движения. Соответственно уменьшается средняя длина свободного пробега и возрастает удельное сопротивление. 3. Почему удельное сопротивление металлических сплавов типа твердых растворов выше, чем у чистых металлов, являющихся компонентами сплава? Ответ: Чистые отожженные металлы имеют менее деформированную кристаллическую решетку, поэтому для них характерны большие значения λ и, следовательно, малая величина ρ 4. Почему металлические сплавы обладают меньшим температурным коэффициентом удельного сопротивления, чем чистые металлы? Ответ: температурный коэффициент удельного сопротивления обратно зависит от удельного сопротивления металла или сплава. Т.к. металлические сплавы обладают большим удельным сопротивлением по сравнению с чистым металлом (см. вопрос 3), то, соответственно, их температурный коэффициент удельного сопротивления будет меньшим, чем в случае чистого металла 5. При каких условиях возникает термоэлектродвижущая сила? Ответ: При наличии разности температур спаев в цепи с термоэлементом появляется термоэлектродвижущая сила (термо-ЭДС), которая состоит из трех составляющих. Первая составляющая термо-ЭДС обусловлена диффузией носителей заряда от нагретого спая к тепловыделяющему спаю. Вторая составляющая термо-ЭДС – это следствие температурной зависимости контактной разности потенциалов. Если оба спая термоэлемента имеют одну и ту же температуру, то контактные разности потенциалов на этих спаях равны, направлены в противоположные стороны и не дают результирующей ЭДС. Если же температуры спаев термоэлемента различны, то значения контактной разности потенциалов на спаях будут также различны. Тогда в цепи термоэлемента появляется вторая составляющая термо-ЭДС с той же полярностью, что и первая составляющая. Третья составляющая термо-ЭДС возникает в термоэлементе вследствие увлечения носителей заряда квантами тепловой энергии – фононами. Если в ветвях термоэлемента есть градиент температуры, то будет существовать направленное движение фононов от нагретых концов ветвей. В результате столкновений фононов с носителями заряда фононы увлекают за собой электроны в отрицательной ветви и дырки в положительной ветви. Этот эффект может оказаться преобладающим при низких температурах. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
