1лабаМЭТ. Основные понятия и определения

Название	Основные понятия и определения
Дата	06.12.2018
Размер	138.52 Kb.
Формат файла
Имя файла	1лабаМЭТ.docx
Тип	Исследование #59024

Цели работы: измерение сопротивлений объемных и тонкопленочных резисторов; исследование зависимостей удельных электрических сопротивлений и их температурных коэффициентов от температуры и состава резистивных материалов, а также зависимостей термоЭДС термопар от разностей температур контактов.

Основные понятия и определения.

Проводниковыми называют материалы, основным электрическим свойством которых является сильно выраженная электропроводность, К основным электрическим характеристикам проводниковых материалов относят: удельное сопротивление ρ, температурный коэффициент удельного сопротивления αρ, удельную термоэлектродвижущую силу αT (термоЭДС).

Наилучшими проводниками электрического тока являются металлы. Механизм протекания тока в металлах заключается в коллективном движении свободных электронов; под действием приложенного электрического поля. В процессе направленного движения электроны испытывают рассеяние на статических (атомы, вакансии, междоузельные атомы и т. д.) и динамических (тепловые колебания ионов в уздах кристаллической решетки) дефектах структуры. Интенсивность рассеяния определяет среднюю длину свободного пробега электрона и, в конечном счете, значение удельного сопротивления проводника, которое может быть выражено следующим образом:

,

где m – масса электрона, e -заряд электрона;

- средняя скорость теплового движения; n₀ - концентрация свободных электронов;

- средняя длина свободного пробега.

Относительное изменение удельного сопротивления при изменении температуры на один Кельвин называют температурным коэффициентом удельного сопротивления

.

В области линейной зависимости ρ(Т) справедливо выражение:

,

где

- удельное сопротивление и температурный коэффициент удельного сопротивления, отнесенные к температуре

.

В технике широко применяются сплавы, имеющие структуру неупорядоченных твердых растворов. Все сплавы имеют повышенное удельное сопротивление в сравнении с компонентами, входящими в их состав. Полное удельное сопротивление сплава

, где

-сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов решетки; ρ_ост- добавочное (остаточное) сопротивление, связанное с рассеянием электронов на неоднородностях структуры сплава. Для многих двухкомпонентных сплавов изменение остаточного сопротивления от состава хорошо описывается параболической зависимостью вида:

, где

- атомные доли компонентов в сплаве.

Описание установки

Измерение сопротивления исследуемых проводников и термоЭДС термопар производится с помощью ампервольтметра Ф-30, постоянно подключенного к испытательному стенду. Все исследуемые образцы расположены В корпусе стенда, причем резисторы R1, R2, R3 и один из спаев термопар помещены в термостат. Подключение образцов к измерительному прибору осуществляется путем нажатия соответствующей кнопки на лицевой панели стенда. Маркировка кнопок соответствует маркировке образцов. Геометрические размеры образцов также указаны на лицевой панели. На время измерения следует удерживать кнопку контакта в утопленном положении.

Экспериментальные результаты

Таблица 1

Материал	Длина l, мм	Толщина d, мм	Ширина b, мм	Диаметр d, мм	Сопротивление R, Ом
1	0,2	0,1	2,5	.	40,2
2	3,25	0,1	2	.	775
3	9,5	0,1	0,6	.	7593
Манганин	1040	.	.	0,1	64,64
Медь	8300	.	.	0,13	10,87
Нихром	900	.	.	0,7	3,8
Константан	1000	.	.	0,06	199,7
Никель	1500	.	.	0,25	3,6

Таблица 2

t_гор, ^оС	t_хол, ^оС	Rт, Ом			∆U_AB, мВ
t_гор, ^оС	t_хол, ^оС	никель	медь	константан	медь-железо	медь-константан	медь-манганин
25	27	17,8	111,2	30,1	-0,02	-0,01	0,01
40	28	18,12	115,2	30,93	0,45	0,44	0,01
55	29	22,68	120,51	31,78	1,07	1,05	0,03
70	29	23	122,78	32,06	1,09	1,35	0,06
85	30	25,5	126,8	32,31	1,7	1,9	0,07
100	30	26	130,8	32,4	2,13	2,25	0,08
115	31	28,13	135,6	32,63	2,68	2,83	0,09
130	32	29,58	137,8	32,68	2,95	3,43	0,1
142	32	30,42	142,4	32,8	3,2	3,56	0,1

Обработка результатов эксперимента

1.1. Расчет удельного сопротивления металлических проводников

Расчет проводим по формуле ρ = RS/l, где R – сопротивление образца, S – площадь его поперечного сечения (π*(d/2)²), l– длина проводника.
Пример расчета для проводника из манганина:

ρ =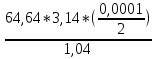

= 0,4882 мкОм*м
Результаты расчета сведены в таблицу:

*Материал__R,_Ом__l,_мм__d,_мм__ρ,_мкОмм'>Материал**	R, Ом	l, мм	d, мм	*ρ, мкОмм**
Манганин	64,64	1040	0,1	0,4882
Медь	10,87	8300	0,13	0,0173
Нихром	3,8	900	0,7	1,625
Константан	199,7	1000	0,06	0,5646
Никель	3,6	1500	0,25	0,1178

1.2. Расчет сопротивления квадрата поверхности металлических пленок

Для расчета используем формулу

R_▫= Rb/l,

где R – сопротивление образца, b – ширина резистивного слоя,

l – длина пленки (расстояние между контактными площадками)
Пример расчета для резистора R1 (медь-железо):
R□ =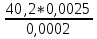

= 502,5 Ом

Результаты вычислений сведены в таблицу:

Материал	R, Ом	b, мм	l, мм	R_▫, Ом
R1	40,2	2,5	0,20	502,5
R2	775	2,0	3,25	476,9
R3	7593	0,6	9,50	479,5

2.1 Таблица зависимости сопротивления резисторов и их температурных коэффициентов удельного сопротивления от температуры

Таблица 1.3

Никель			Медь		Константан
t, ˚C	α_ρ, K^-1	R_t, Ом	αρ, K-1	R_t, Ом	αρ, K-1	R_t, Ом
25	0,014625	17,8	0,0116148	111,2	0,010552	30,1
40	0,014367	18,12	0,0112119	115,2	0,010269	30,93
55	0,011482	22,68	0,0107185	120,51	0,009995	31,78
70	0,011322	23	0,0105205	122,78	0,009908	32,06
85	0,010214	25,5	0,0101874	126,8	0,009831	32,31
100	0,010018	26	0,0098763	130,8	0,009804	32,4
115	0,00926	28,13	0,0095271	135,6	0,009735	32,63
130	0,008807	29,58	0,0093752	137,8	0,00972	32,68
142	0,008565	30,42	0,0090728	142,4	0,009684	32,8

график зависимости сопротивления материалов от температуры

3. Расчет температурного коэффициента удельного сопротивления

Рассчитаем температурный коэффициент удельного сопротивления α_ρ, пользуясь выражением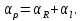

Для этого воспользуемся программой MSExcel и с помощью функции ЛИНЕЙН() (аппроксимация исходных данных линейной зависимостью y=k*x+b, производная dR/dT при данной температуре равна

коэффициенту k) найдем значение производных.
Значения dR/dT:

для меди 1,29 Ом/К;

для никеля 0,26 Ом/К;

для константана 0,317 Ом/К.
Температурные коэффициенты расширения α_l:
для меди 16,7*10^-6

для никеля 12,8*10^-6

для константана 17*10^-6
Пример расчета для Никеля при t₁=25^oC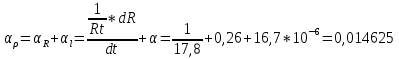

K^-1
Результаты расчетов для остальных резисторов занесены в таблицу 1.3 выше.

4. Построим зависимость α_ρ = f(t) для исследованных материалов
График зависимости коэффициента удельного сопротивления от температуры для никеля, меди и константана

5. Рассчитаем зависимость удельного сопротивления и температурного коэффициента удельного сопротивления от состава для сплавов системы Cu-Ni при комнатной температуре

Рассчитаем значения удельного сопротивления сплавов из формулы:

ρ_Cu_-_Ni = ρ_Nix_Ni + ρ_Cu(1-x_Ni) + Cx_Ni(1 – x_Ni)
Коэффициент С находим, подставляя вместо ρ_Cu_-_Ni значение удельного сопротивления константана, а x_Ni принимаем равным 0,4, так как содержание никеля в константане равно 40%.

Коэффициент С равен 2,150*10^-6.

Значения температурного коэффициента удельного сопротивления находим по формуле: αρ_Cu_-_Ni= (1/ ρ_Cu_-_Ni)[ αρ_Cu*ρ_Cu(1-x_Ni) + ρ_Nix_Niαρ_Ni],
Пример расчета для x_Ni= 0, Значения αρ для никеля и меди брались при температуре 25˚C :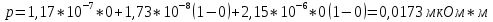

α_ρ=(1/0,0173)[(1-0)*0,011*1,73*10^-8+1,17*10^-7*0*0,014625]=0,0116 K^-1
Результаты расчетов для остальных параметров x_Ni занесены в таблицу 1.5 ниже.
Таблица 1.5

x_Ni	0	0,2	0,4	0,6	0,8	1
ρ, мкОм*м	0,0173	0,3814	0,5735	0,5936	0,4417	0,1178
α_ρ, К^-1	0,0116	0,0013	0,0014	0,0009	0,0018	0,0146

6. Графики зависимостей ρ(x_ni-cu) и αρ(x_ni-cu)

График зависимости удельного сопротивления сплава от его состава
График зависимости температурного коэффициента удельного сопротивления сплава от состава сплава

7. Температурные зависимости термоЭДС для исследованных термопар
Медь-железо

График зависимости термоЭДС термопары медь-железо от разности температур

Медь-константан

График зависимости термоЭДС термопары медь-константан от разности температур
Медь-манганин

График зависимости термоЭДС термопары медь-манганин от разности температур

8. Выводы

В ходе лабораторной работы было выяснено, что удельное сопротивление сплава больше любого из удельных сопротивлений металлов, входящих в этот сплав, так как происходит взаимообусловленное нарушение периодичности кристаллических структур.

Сопротивление константана практически не меняется в широком диапазоне температур.

Удельное сопротивление сплава имеет параболическую зависимость от содержания в сплаве одного из его компонентов.