1-37 теория. 1. Первообразная и ее свойства. Неопределенный интеграл, его свойства
 Скачать 79.13 Kb. Скачать 79.13 Kb.
|
|
1. Первообразная и ее свойства. Неопределенный интеграл, его свойства. Функция F(x) называется первообразной f(x) если 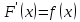 Cвойства Если  так же первообразная f(x) где C-любая постоянная ( так же первообразная f(x) где C-любая постоянная (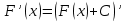 ) )Если 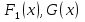 две первообразные одной и той же функции f(x) на (a,b) то две первообразные одной и той же функции f(x) на (a,b) то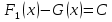 ( (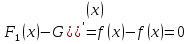 Свойства неопределенного интеграла 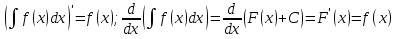 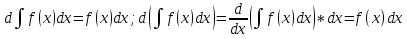 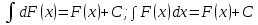 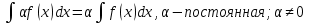 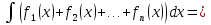 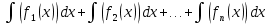 2. Интегрирование простейших дробей 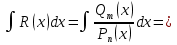 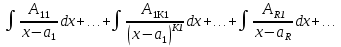 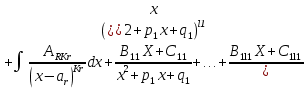 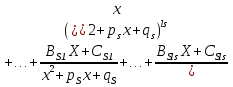 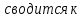 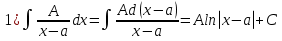 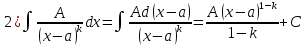 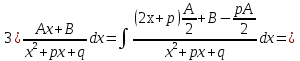 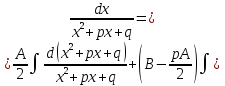 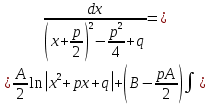 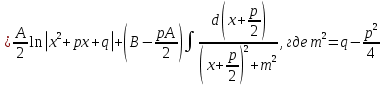 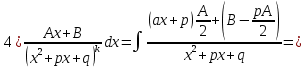 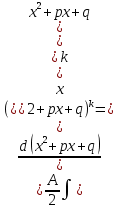 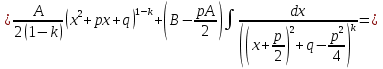 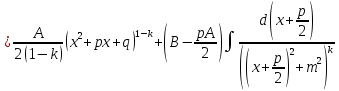 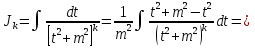 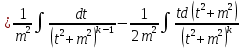 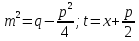 3. Свойства определенного интеграла. Доказать теорему о сохранении определенным интегралом знака подынтегральной функции. Свойства 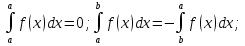 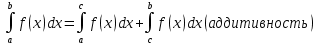 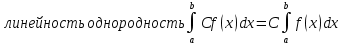 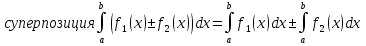 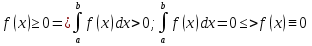 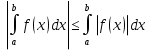 Теорема 1) f(x) интегрируема на [a,b]; 2) 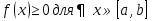 Тогда Тогда 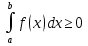 Доказательство: Пусть 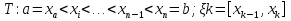 . Составим интегральную сумму f(x) на [a,b]: . Составим интегральную сумму f(x) на [a,b]: 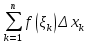 т.к т.к 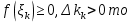 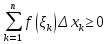 Переходя к переделу при d(T)->0  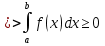 4. Свойства определенного интеграла. Доказать теорему о оценке определенного интеграла знака подынтегральной функции. Свойства 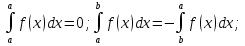 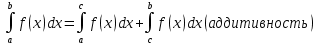 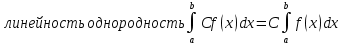 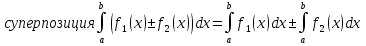 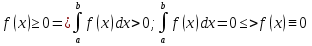 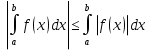 Теорема Если f(x) интегрируема на на 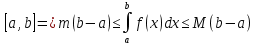 , m,M – минимальное и максимальное значение f(x) на [a,b] , m,M – минимальное и максимальное значение f(x) на [a,b]Док левого неравнества. Правое доказывается аналогично 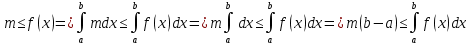 5. Доказать теорему об оценке модуля определенного интеграла. Свойства 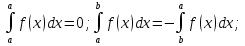 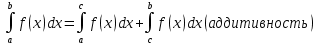 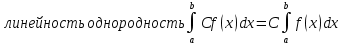 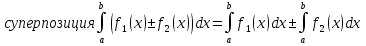 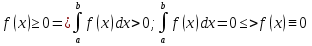 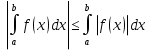 Т Пусть f(x) интегрируема на [a,b] тогда 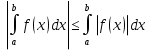 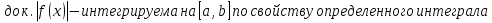 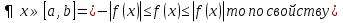 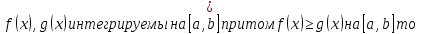 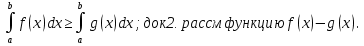 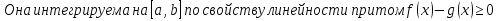  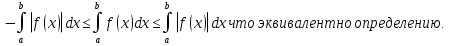 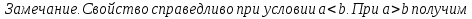 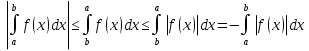 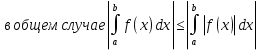 6. Доказать теорему о среднем для определенного интеграла. Свойства 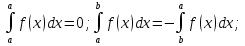 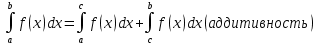 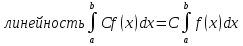 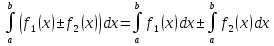 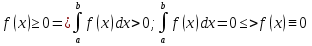 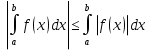 Т.  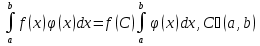 Док-во 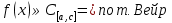 ||т. Вейерштрасса Пусть дана непрерывная числовая функция, определённая на отрезке, то есть 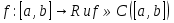 . Пусть . Пусть 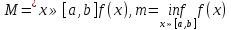 — точные верхняя и нижняя границы множества значений функции f соответственно. Тогда эти значения конечны 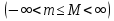 и достигаются (существуют и достигаются (существуют 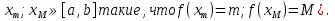 || || 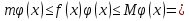 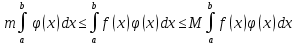 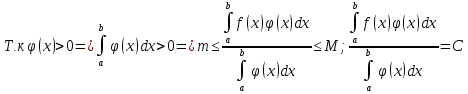 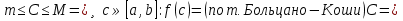 //т. Больцано-Коши. Пусть дана непрерывная функция на отрезке 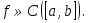 Пусть также Пусть также 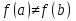 , и без ограничения общности предположим, что f(a) = A < B = f(b). Тогда для любого , и без ограничения общности предположим, что f(a) = A < B = f(b). Тогда для любого 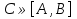 существует существует 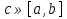 такое, что f(c)=C. // такое, что f(c)=C. //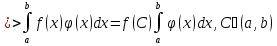 7. Сформулировать определение интеграла с переменным верхним пределом. Доказать теорему о производной от интеграла по его верхнему пределу. 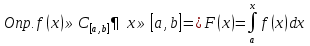 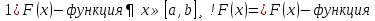 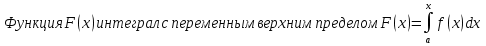 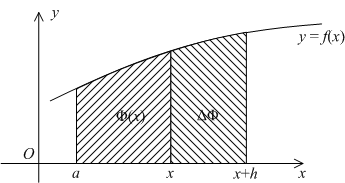 Теорема. Пусть f(x) интегрируема на [a,b] и нерперывна в некоторой точке x этого отрезка тогда функция 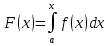 дифференцируема в точке x и F’(x)=f(x) дифференцируема в точке x и F’(x)=f(x)Док.во 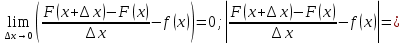 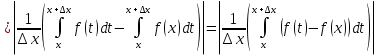 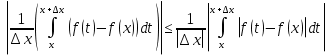 Т.к f непрерывна в точке 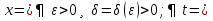 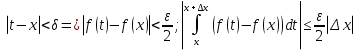 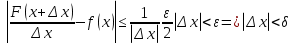 8. Вывести формулу Ньютона-Лейбница Свойства 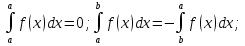 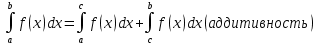 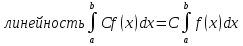 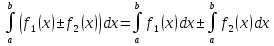 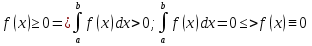 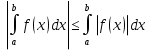 Ф 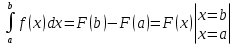 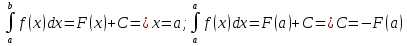 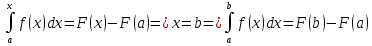 9. Сформулировать и доказать теорему об интегрировании подстановкой для неопределенного инетграла. 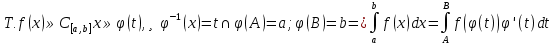 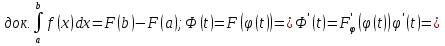 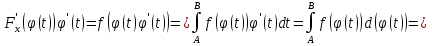 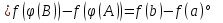 10. Сформулировать и доказать теорему об интегрировании по частям для определенного инетграла. 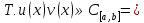 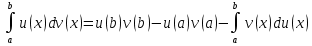 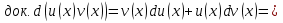 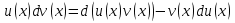 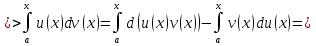 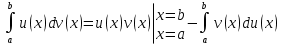 11. Интегрирование периодических функций, интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат. 1) Функция периодическая с периодом T 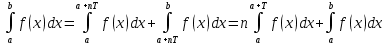 2) Функция четная или нечетная 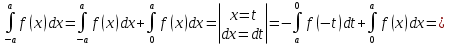 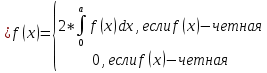 12. Сформулировать определение несобственного интеграла 1-ого рода. Сформулировать и доказать признак сходимости по неравнеству для неопределенного интеграла 1-ого рода. Опр. f(x) непрерывна на 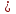 . Несобственный интеграл 1-ого рода . Несобственный интеграл 1-ого рода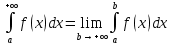 Теорема 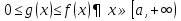 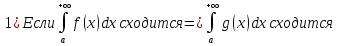 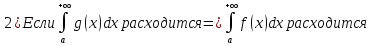 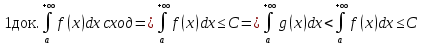 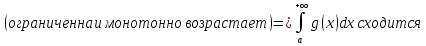 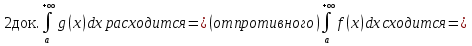 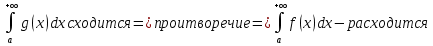 13. Сформулировать определение несобственного интеграла 1-го рода. Сформулировать и доказать предельный признак сравнения для несобственных интегралов 1-го рода Пусть 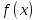 непрерывна на непрерывна на 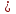 . .Неопределенным интегралом первого рода называется: 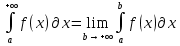 Предельный признак сравнения: Пусть 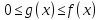 и и 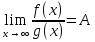 , тогда: , тогда: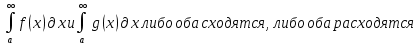 Доказательство: 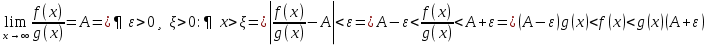 Значит: 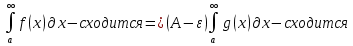 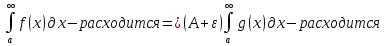 14. Сформулировать определение несобственного интеграла 1-го рода. Сформулировать и доказать признак абсолютной сходимости для несобственных интегралов 1-го рода: Пусть 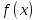 непрерывна на непрерывна на 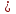 . .Неопределенным интегралом первого рода называется: 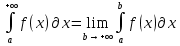 Признак абсолютной сходимости: Пусть 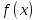 непрерывна на непрерывна на  : :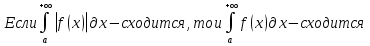 Доказательство: 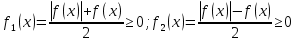 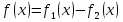 Значит: 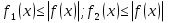 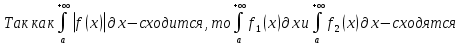 Значит: 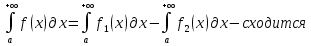 15. Сформулировать определение несобственного интеграла 2-го рода и признаки сходимости таких интегралов: Пусть 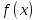 интегрируема на любом отрезке интегрируема на любом отрезке 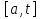 , где , где 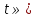 . .Пусть f не является ограниченной в окрестности 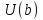 точки точки 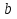 . .Тогда несобственным интегралом 2-го рода называется: 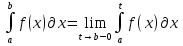 1.Признак сравнения по неравенству: Пусть 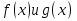 интегрируемы на любом отрезке интегрируемы на любом отрезке 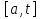 , где , где 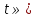 и для и для 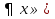 выполняется неравенство выполняется неравенство 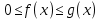 , тогда: , тогда: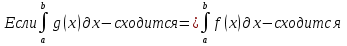 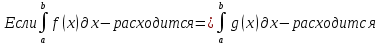 2.Предельный признак сравнения: Пусть 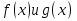 интегрируемы на любом отрезке интегрируемы на любом отрезке 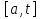 , где , где 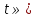 и и 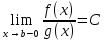 , , 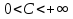 , ,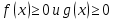 для для 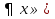 , тогда: , тогда: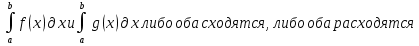 3.Признак абсолютной сходимости: Пусть 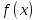 интегрируема на любом отрезке интегрируема на любом отрезке 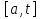 , где , где 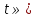 , тогда: , тогда: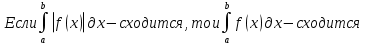 16. Фигура ограничена кривой y = f(x) > 0, прямыми x = a, x = b и y = 0 (a < b). Вывести формулу для вычисления с помощью определенного интеграла площади этой фигуры: 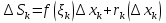 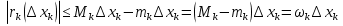 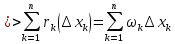 Из необходимого и достаточного условия: 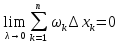 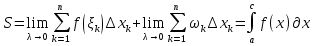 Если f(x) < 0 : 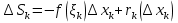 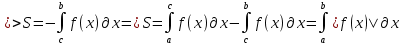 17. Фигура ограничена лучами ϕ = α, ϕ = β и кривой r = f(ϕ). Здесь r и ϕ — полярные координаты точки, 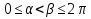 , где r и ϕ — полярные координаты точки. Вывести формулу: , где r и ϕ — полярные координаты точки. Вывести формулу: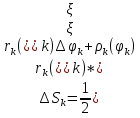 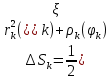 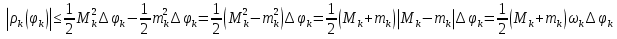 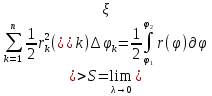 для вычисления с помощью определенного интеграла площади этой фигуры 18. Тело образовано вращением вокруг оси  криволинейной трапеции, ограниченной кривой y = f(x) > 0, прямыми x = a, x = b и y = 0 (a < b). Вывести формулу для вычисления с помощью определенного интеграла объема тела вращения: криволинейной трапеции, ограниченной кривой y = f(x) > 0, прямыми x = a, x = b и y = 0 (a < b). Вывести формулу для вычисления с помощью определенного интеграла объема тела вращения: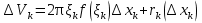 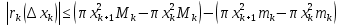 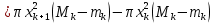 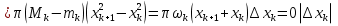 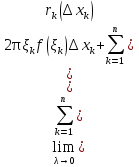 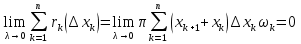 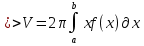 19. Кривая задана в декартовых координатах уравнением y = f(x), где x и y — декартовые координаты точки, 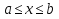 . Вывести формулу для вычисления длины дуги этой кривой: . Вывести формулу для вычисления длины дуги этой кривой:Пусть  непрерывно дифференцируемая на непрерывно дифференцируемая на 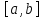 функция. Тогда дуга графика функции функция. Тогда дуга графика функции 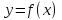 , отсекаемая прямыми , отсекаемая прямыми 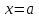 и и 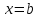 является спрямляемой, причем: является спрямляемой, причем: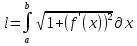 Доказательство: 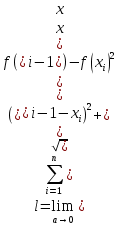 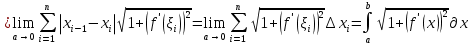 Если интеграл существует 20. Кривая задана в полярных координатах уравнением 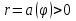 , где r и , где r и 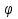 — полярные координаты точки, — полярные координаты точки, 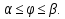 Вывести формулу для вычисления длины дуги этой кривой: Вывести формулу для вычисления длины дуги этой кривой: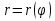 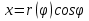 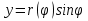 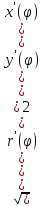 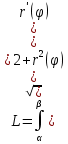 21. ЛДУ 1-го порядка. Интегрирование ЛДУ 1-го порядка методом Бернулли (“u*v”) и методом Лагранжа (вариация произвольной постоянной) ЛДУ 1-го порядка это уравнение линейное относительно неизвестной функции и её производной и имеет вид: 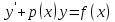 , где , где 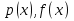 – заданные функции от x, непрерывные в области отыскания решения уравнений ( – заданные функции от x, непрерывные в области отыскания решения уравнений (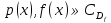 ). Если ). Если 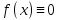 , то данное уравнение называется линейным однородным, иначе – неоднородным. , то данное уравнение называется линейным однородным, иначе – неоднородным. Методы решения НЛДУ 1-го порядка:
Метод Лагранжа: рассмотрим 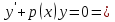 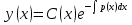 , тогда , тогда 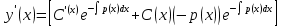 , согласно , согласно 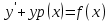 получаем: получаем: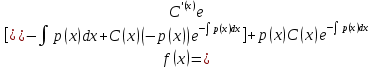 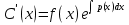 ; ; 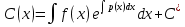 => => 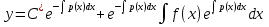 ; первая часть суммы – общее решение ЛОДУ; вторая – частное решение ЛНДУ ; первая часть суммы – общее решение ЛОДУ; вторая – частное решение ЛНДУМетод Бернулли: пусть 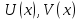 - произвольные функции, - произвольные функции, тогда 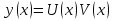 , , 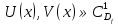 , согласно , согласно 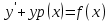 получаем: получаем: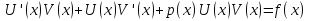 , ,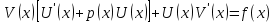 , ,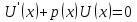 => => 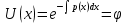 => => 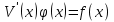 , тогда определим V(x): , тогда определим V(x): 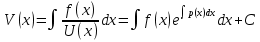 , мы нашли U(x) и V(x), теперь: , мы нашли U(x) и V(x), теперь: 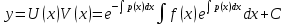 22) Сформулировать теорему Коши о существовании и единственности решения дифференциального уравнения n-го порядка. Интегрирование дифференциальных уравнений n-го порядка, допускающих понижение порядка. Т. Коши: 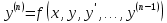 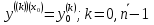     Интегрирование:                 23. Сформулировать теорему Коши о существовании и единственности решения ЛДУ n-го порядка. Доказать св-ва частных решений ЛОДУ n-го порядка. Теорема: пусть функция  и её частные производные и её частные производные  определены и непрерывны в некоторой области определены и непрерывны в некоторой области  . Тогда в любой внутренней точке . Тогда в любой внутренней точке  существует единственное решение ДУ, удовлетворяющее начальным условиям (т.е. существует единственное решение ДУ, удовлетворяющее начальным условиям (т.е.  , … , , … , 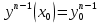 ) )Св-ва: 1: пусть 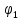 и и 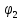 – частные решения ОЛДУ, – частные решения ОЛДУ, 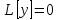 . Тогда . Тогда  + +  – решение ОЛДУ. Док-во: – решение ОЛДУ. Док-во:  и и  => => 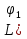 + + 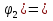 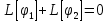 . 2: пусть . 2: пусть 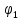 – решение ОЛДУ, – решение ОЛДУ, 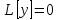 . Тогда . Тогда 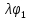 -решение ОЛДУ, -решение ОЛДУ, 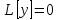 . Док-во: . Док-во: 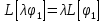 , , 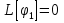 => => 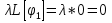 . 3: пусть . 3: пусть 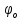 – частное решение ОЛДУ, – частное решение ОЛДУ, 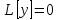 и и  – частные решения НЛДУ, – частные решения НЛДУ,  . Тогда: . Тогда:  - решение НЛДУ, - решение НЛДУ,  . Док-во: . Док-во: 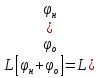 24) Сформулировать определения линейно зависимой и линейно независимой систем функций. Сформулировать и доказать теорему о вронксиане линейно зависимых функций. 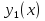 , … , , … , 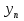 (x) линейно зависима, если хотя бы одно (x) линейно зависима, если хотя бы одно 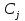 0, а линейная комбинация 0, а линейная комбинация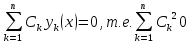 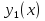 , … , , … , 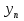 (x) линейно независима, если (x) линейно независима, если  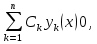 только когда все только когда все 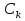 = 0, K = = 0, K = 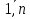 x [a,b] x [a,b] Теорема: Теорема: 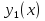 , … , , … , 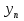 (x) линейно зависима ѡ( (x) линейно зависима ѡ(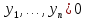 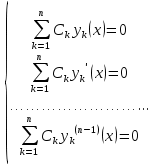 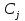 0 0( 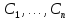 ) 0 ) 0 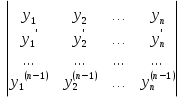 = 0 = 0 25. Определения линейно зависимой и линейно независимой систем функций. Теорема о вронскиане системы линейно независимых частных решений линейного однородного дифф уравнения n-го порядка. 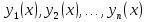 – лин. НЕзав. если: – лин. НЕзав. если: 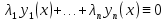 => => 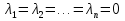 . .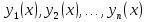 – лин. ЗАВ. если: – лин. ЗАВ. если: 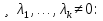 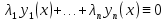 . .Вронксианом системы n-1 раз дифф функций 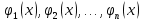 называется функциональный определитель называется функциональный определитель 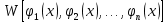 = = 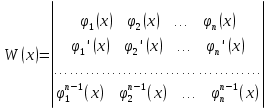 , , 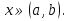 Теорема: 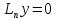 , ,  : :  , ,  , ,  – линейно независима – линейно независима 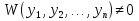 . Док-во (от противного): Необходимость: т.к. . Док-во (от противного): Необходимость: т.к. 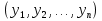 – линейно независима => – линейно независима => 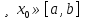 и и 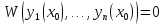 . Тогда: . Тогда:  Данная система имеет определитель равный нулю => в т. Данная система имеет определитель равный нулю => в т.  : :  => в силу теоремы единственности получаем противоречие => => в силу теоремы единственности получаем противоречие =>  => => 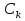 не все равны нулю. Достаточность: пусть не все равны нулю. Достаточность: пусть 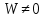 в окр. т. в окр. т. 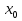 , то решения линейно зависимы, но это противоречит теореме о вронскиане СЛ зависимых решений (Если система функций , то решения линейно зависимы, но это противоречит теореме о вронскиане СЛ зависимых решений (Если система функций 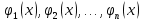 линейно зависима на интервале (a,b) , то линейно зависима на интервале (a,b) , то 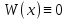 ) )26) Сформулировать и доказать теорему о существовании фундаментальной системы решений линейного однородного дифференциального уравнения n-го порядка.   , …, , …,  - линейно независимое решение - линейно независимое решениеД.  y 0 y 0  0, k = 0, k =  Существ. системы решений ѡ Существ. системы решений ѡ 0 в т. ее окр-ти 0 в т. ее окр-ти27. Теорема о структуре общего решения линейного однородного дифф уравнения n-го порядка Теорема: 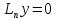 , , 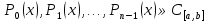 => => 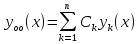 , где , где 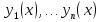 – независимые решения. Док-во: возьмём – независимые решения. Док-во: возьмём 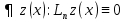 , значит: , значит: 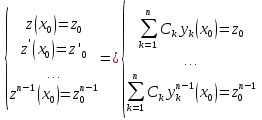 => => 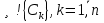 => в силу единственности по т. Коши : => в силу единственности по т. Коши : 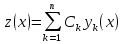 => => 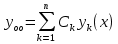 28) Вывести формулу Остроградского-Лиувилля для линейного дифференциального уравнения 2-го порядка. 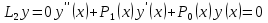 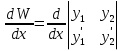 = = 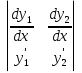 + +  = =       29. Формула для общего решения линейного однородного дифф уравнения 2-го порядка при одном известном частном решении.  – ОЛДУ 2-го порядка. Пусть – ОЛДУ 2-го порядка. Пусть 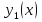 – известное решение. – известное решение. 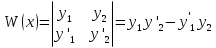 . Тогда . Тогда 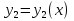 – искомое решение. В то же время по формуле Остоградского –Лиувилля: – искомое решение. В то же время по формуле Остоградского –Лиувилля: 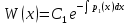 . Получаем: . Получаем:   => =>  => =>  => =>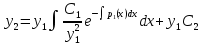 . При . При 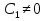 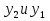 – линейно независимы. – линейно независимы. 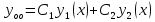 30. Сформулировать и доказать теорему о структуре общего решения линейного неоднородного дифференциального уравнения n-го порядка. T. 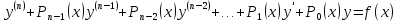 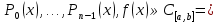 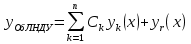 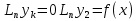 Док-во: 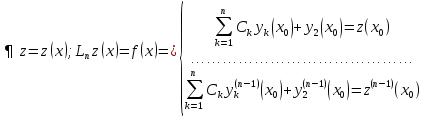 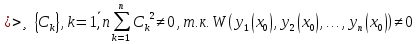 31. Вывести формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае кратных корней характеристического уравнения. 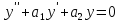 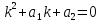 - характеристическое уравнение - характеристическое уравнение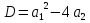 -дискриминант -дискриминант 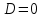 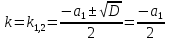 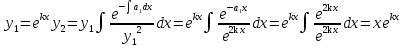 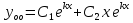 32. Вывести формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. 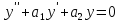 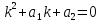 - характеристическое уравнение - характеристическое уравнение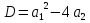 -дискриминант -дискриминант 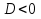 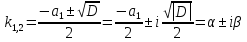 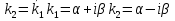 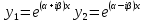 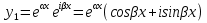 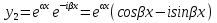 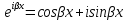 - формула Эйлера - формула Эйлера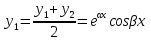 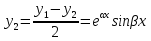 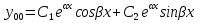 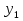 и и 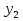 - линейно независимы - линейно независимы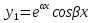 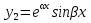 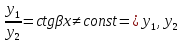 - линейно независимы => - линейно независимы =>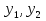 образуют ФСР образуют ФСР33. Частное решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами и правой частью специального вида (являющейся квазимногочленом). Сформулировать и доказать теорему о наложении частных решений. Определение: Квазимногочленом называется сумма нескольких слагаемых вида 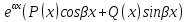 где 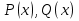 - многочлены - многочленыЧастное решение уравнения 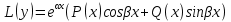 ищется в виде ищется в виде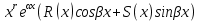 где 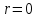 , если , если 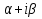 не корень характеристического уравнения, и не корень характеристического уравнения, и 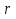 равно кратности этого корня, в противном случае; равно кратности этого корня, в противном случае; 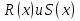 - многочлены с неопределенными коэффициентами, степень каждого из которых равна максимальной из степеней - многочлены с неопределенными коэффициентами, степень каждого из которых равна максимальной из степеней 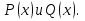 Т. 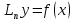 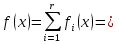 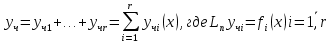 Док-во: 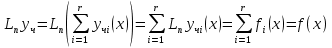 34. Метод Лагранжа вариации произвольных постоянных для нахождения решения линейного неоднородного дифференциального уравнения 2-го порядка и вывод системы соотношений для варьируемых переменных. 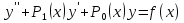 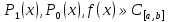 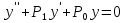 имеет 2 линейных независимых решения имеет 2 линейных независимых решения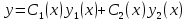 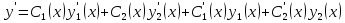 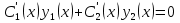 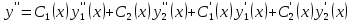 Подставим в уравнение 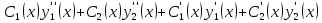 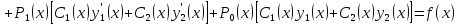 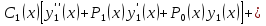 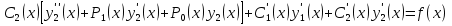 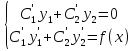 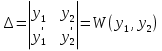 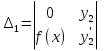 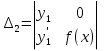 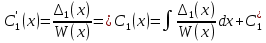 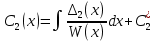 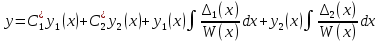 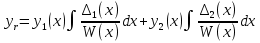 35. Сформулировать определение дифференциального уравнения n-го порядка, разрешенного относительно старшей производной, и сформулировать задачу Коши для такого уравнения. Описать метод сведения этого уравнения к нормальной системе дифференциальных уравнений. ДУ n-го порядка, разрешенное относительно старшей производной, уравнение вида 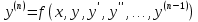 Задача Коши 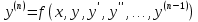 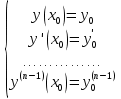 условие Коши условие КошиСведение ДУ n-го порядка к нормальной системе 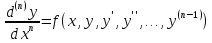 Замена переменных 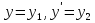 , ... , , ... , 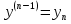 => =>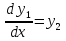 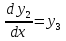  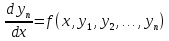 36. Сформулировать задачу Коши для нормальной системы дифференциальных уравнений и теорему Коши о существовании и единственности решения этой задачи. Описать метод сведения нормальной системы к одному дифференциальному уравнению высшего порядка. Определение: Нормальной системой называется система вида: 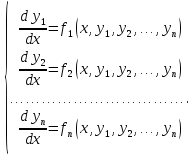 Задача Коши: 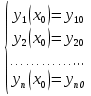 Теорема Коши:     Сведение системы к ДУ  Берем любое уравнение     Из 1-го уравнения находим    условие разрешимости условие разрешимости37. Сформировать определение первого интеграла нормальной системы дифференциальных уравнений. Описать методы нахождения первых интегралов и их применение для решения системы дифференциальных уравнений. Рассмотрим систему  Функция  называется первым интегралом нормальной системы дифференциальных уравнений если эта функция нерпрерывна, имеет непрерывные частные производные по x,y1, … yn и при подстановке в нее любого решения системы она сохраняет постоянный знак. Пусть называется первым интегралом нормальной системы дифференциальных уравнений если эта функция нерпрерывна, имеет непрерывные частные производные по x,y1, … yn и при подстановке в нее любого решения системы она сохраняет постоянный знак. Пусть  -решение нормальной системы, а функция -решение нормальной системы, а функция  ее первый интеграл. Тогда сформулированное определение означает что ее первый интеграл. Тогда сформулированное определение означает что  . Для разных решений число c-разное. Для фиксированного решения – это константа. . Для разных решений число c-разное. Для фиксированного решения – это константа.Нахождение 1х интегралов Рассмотрим систему  Для нахлждения 1х интегралов обычно используют метод выделения интегрируемых комбинаций с помощью арифметических операций. С помощью арифметических операций уравнение системы приводят к виду  Функция  в этих соотношениях является 1-м интегралом системы. Для нахождения интегрируемых комбинаций бывает удобно записать нормальную систему в симметрической форме. Чтобы ее получить из каждого уравнения системы dx и приравнять полученное выражение. в этих соотношениях является 1-м интегралом системы. Для нахождения интегрируемых комбинаций бывает удобно записать нормальную систему в симметрической форме. Чтобы ее получить из каждого уравнения системы dx и приравнять полученное выражение. Это симметрическая форма записи нормальной системы. Чтобы найти интегрируемую комбинацию нужно выделить пару отношений, допускающую разделение переменных либо воспользоваться свойством равных дробей. Свойства равных дробей. Если  Для его доказательства достаточно заметить что  Коэфициенты  стараются подобрать так чтобы знаменатель полученно дроби был =0, а числитель являлся полным дифференциалом некоторой функции стараются подобрать так чтобы знаменатель полученно дроби был =0, а числитель являлся полным дифференциалом некоторой функции  тогда эта функция первый интеграл. тогда эта функция первый интеграл.Получение решния нормальной системы при помощи 1-х интегралов. Матрицей Якоби системы функций  ,…, ,…,  по части переменных по части переменных  называют матрицу называют матрицу Определитель матрицы Якоби называется Якобианом. Рассмотрим нормальную систему n-ого порядка  Пусть известны n 1-х интегралов этой системы:  ,…, ,…,  Опр. Первые интегралы  ,…, ,…,  системы называются независимыми в области D если в каждой точке области матрица Якоби невырождена (Якобиан отличен от нуля во всех точках области). Пусть первые интегралы системы называются независимыми в области D если в каждой точке области матрица Якоби невырождена (Якобиан отличен от нуля во всех точках области). Пусть первые интегралы  ,…, ,…,  системы (1) независимы. системы (1) независимы.Тогда можем показать, что в этом случае система соотношений  Где  произвольные постоянные задает решение системы (1) и является по поределению общим интегралом этой системы. Для того чтобы решить систему (1) достаточно найти n 1-х интегралов этой системы и убедиться что они независимы. произвольные постоянные задает решение системы (1) и является по поределению общим интегралом этой системы. Для того чтобы решить систему (1) достаточно найти n 1-х интегралов этой системы и убедиться что они независимы. |
