Редукторы. 1. Подбор чисел зубьев в соосном двухступенчатом планетарном цилиндрическом редукторе
 Скачать 64.99 Kb. Скачать 64.99 Kb.
|
|
1. Подбор чисел зубьев в соосном двухступенчатом планетарном цилиндрическом редукторе. При проектировании планетарных механизмов наиболее трудоемким этапом в расчете геометрии является подбор чисел зубьев. Широко применяемым методом подбора является метод сомножителей. При выборе схемы механизма следует руководствоваться величиной передаточного отношения U12. Заданное передаточное отношение обеспечивается подбором числа зубьев z1, z2, z3, z4. При подборе чисел зубьев необходимо обеспечить несколько условий одновременно. Это УСЛОВИЕ СООСНОСТИ, УСЛОВИЕ СОСЕДСТВА, УСЛОВИЕ СБОРКИ центрального, корончатого колес и сателлитов. Условие соосности способствует обеспечению равенства межосевых расстояний центрального колеса и сателлитов. Условие соседства обеспечивает размещение сателлитов без задевания одного другим. Условие сборки обеспечивает возможность собираемости N-oгo количества сателлитов после установки первого так, чтобы зубьям сателлитов обеспечивалась возможность расположения во впадинах центрального и корончатого колес одновременно. Сущность подбора чисел зубьев методом сомножителей состоит в том, что отношение чисел зубьев, входящих в формулу для определения передаточного отношения U12 представляется отношением так называемых сомножителей С1, С2, С3, С4. Затем записывается условие соосности для данной схемы планетарного механизма (свое для каждой схемы), в котором неизвестное число зубьев выразится через известные сомножители. Далее, налагая условие сборки (практически одинаковое для всех схем планетарных механизмов), получают искомое число зубьев. Например, для схемы 2 передаточное отношение определяется формулой: и равно числу 5,20, которое можно представить суммой 1+4,20 или иначе 1+42/10=1+21/5. Последнюю дробь можно представить в виде произведения двух сомножителей числителя и двух сомножителей знаменателя, и тогда формулу для определения передаточного отношения можно переписать в цифровом выражении введя сомножители С1, С2, С3, С4: Имеется двухступенчатый планетарный редуктор с общим передаточным числом 48,84 Выбираем передаточное число первой ступени uред.1 = 8. Тогда передаточное число второй ступени редуктора uред.2 = 6,11. 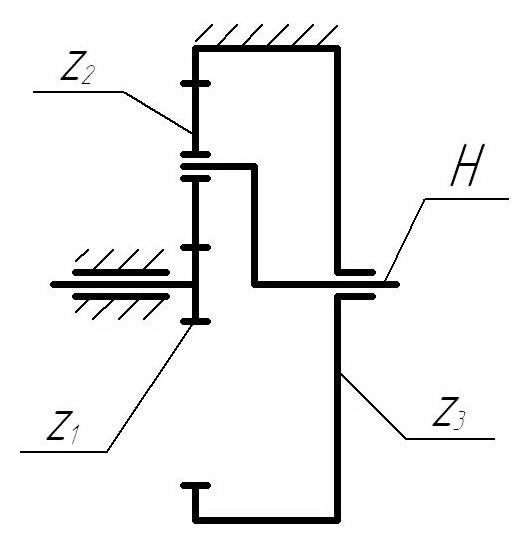 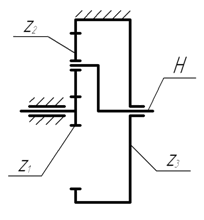 1 < U < 10 1 < U < 10 uред.1=8 uред.1=6,11 ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ ЧИСЛО ЗУБЬЕВ ИЗ УСЛОВИЯ СООСНОСТИ ПО МЕТОДУ СОМНОЖИТЕЛЕЙ z1=γ c1 z1=γ c1 15=5 х 3 21=3 х 7 z3=γ c3 z3=γ c3 105=5 х 21 108=3 х 36 УСЛОВИЕ СБОРКИ N, M – целые числа k - число сателлитов планетарной передачи, выберем равное 3-м УСЛОВИЕ СОСЕДСТВА 0,78 ≤ 0,87 0,71 ≤ 0,87 2. Волновые передачи. Передаточное отношение волнового редуктора при неподвижном гибком или жестом звене (зубчатом колесе). Волновыми называют механические передачи, содержащие контактирующие между собой гибкое и жесткое звенья и обеспечивающие передачу и преобразование движения путем деформирования гибкого звена. Волновые передачи бывают фрикционные, зубчатые и винтовые. У зубчатых волновых передач гибкие колеса имеют наружные, а жесткие колеса — внутренние зубья. В настоящее время такие передачи имеют основное распространение. Достоинства волновых зубчатых передач заключаются в возможности получения значительных передаточных чисел, небольшой массе и габаритах конструкции, высокой кинематической точности передачи, являющейся результатом многопарного зацепления зубьев. Волновые зубчатые передачи долговечны и имеют более низкий уровень шума по сравнению с обычными зубчатыми передачами. К недостаткам волновых зубчатых передач следует отнести сложную технологию изготовления деталей и отсутствие конструкций, у которых оси пересекаются или скрещиваются. Волновые передачи в наше время начинают применять в станкостроении, подъемно-транспортных машинах, химическом машиностроении, авиационной и ракетной технике, промышленных роботах и др. В волновой фрикционной передаче передаточное отношение зависит от разности диаметров жесткого и гибкого колес и равно отношению диаметра ведомого колеса к разности диаметров колес. Заменяя отношение диаметров колес отношением чисел их зубьев, получим передаточное отношение и для волновой зубчатой передачи: при ведомом жестком колесе: u = ωh/ωb=zb/(zb-zg); при ведомом гибком колесе: u = ωh/ωg=zg/(zb-zg); где zb, zg— числа зубьев жесткого и гибкого колес. Очевидно, что для увеличения передаточного отношения разность чисел зубьев колес должна быть возможно меньшей, причем она должна быть равной или кратной числу волн деформации генератором гибкого колеса во избежание интерференции (наложения) зубьев. |
