1. Поколения вычислительных машин. 5

• Название: 1. Поколения вычислительных машин. 5
• Дата: 30.05.2022
• Размер: 2.93 Mb.
• Имя файла: ovs_voprosy.docx
• Тип: Документы; #557969
• страница: 24 из 38

71. Виды кабельной продукции и разъемы для соединения витой пары. Раскладки проводов витой пары.

В зависимости от наличия защиты — электрически заземлённой медной оплетки или алюминиевой фольги вокруг скрученных пар, определяют разновидности данной технологии:

• 
  незащищенная витая пара (UTP — Unshielded twisted pair) — какие-либо защита или экранирование отсутствуют;
  
• 
  фольгированная витая пара (FTP — Foiled twisted pair) — также известна как S/UTP присутствует один общий внешний экран;
  
• 
  защищенная витая пара (STP — Shielded twisted pair) — присутствует экран для каждой пары;
  
• 
  фольгированная экранированная витая пара (S/FTP — Shielded Foiled twisted pair) — отличается от FTP наличием дополнительного внешнего экрана из медной оплетки;
  
• 
  защищенная экранированная витая пара (S/STP — Screened shielded twisted pair) — отличается от STP наличием дополнительного общего внешнего экрана.
  

Каждый провод внутри кабеля может быть одножильным и многожильным - состоящим из 7 проволочек.

Одножильный имеет лучшие характеристики, но применяется только на стационарных линиях.

Существуют разъёмы неразъёмные - для STP, и разъёмные, например, RJ-45.

Коннекторы обычно устанавливаются без пайки, так как применяется технология IDC - при подключении изоляция смещается, то есть применяются контакты-ножи.

RJ11 представляет собой стандарт 6P4C (6 разъемов, 4 контакта), где есть только четыре провода с контактами. RJ45 - 8P8C (8 разъёмов, 8 контактов).

Существует два варианта обжима разъёма на кабеле:

• 
  для создания прямого кабеля — для соединения порта сетевой карты с коммутатором или концентратором,
  
• 
  для создания перекрёстного (использующего кроссированный MDI, англ. MDI-X) кабеля, имеющего инвертированную разводку контактов разъёма для соединения напрямую двух сетевых плат, установленных в компьютеры, а также для соединения некоторых старых моделей концентраторов или коммутаторов (uplink-порт).
  

Прямой кабель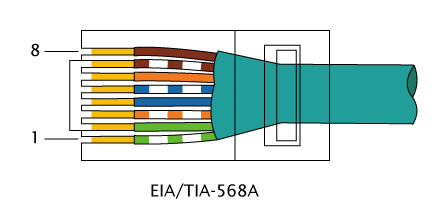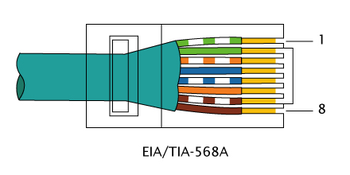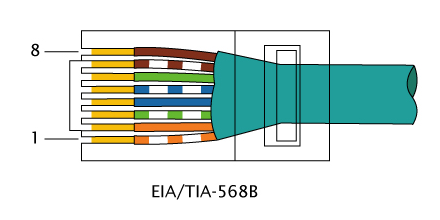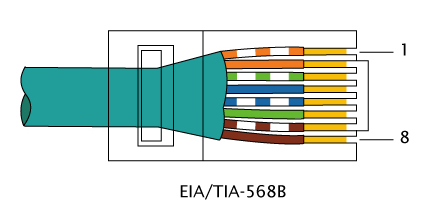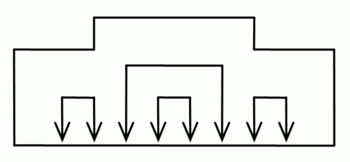







При соединении EIA/TIA-568A 1: Бело-зеленый 2: Зелёный 3: Бело-оранжевый 4: Синий 5: Бело-синий 6: Оранжевый 7: Бело-коричневый 8: Коричневый.

При соединении EIA/TIA-568B, AT&T 258A 1: Бело-оранжевый 2: Оранжевый 3: Бело-зелёный 4: Синий 5: Бело-синий 6: Зелёный 7: Бело-коричневый 8: Коричневый.

Перекрёстный кабель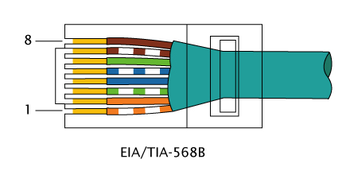

72. Алгоритм сжатия информации. Алгоритм Хаффмена. Алгоритм Лемпеля-Зива

Сжа́тие да́нных (англ. datacompression) — алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма. Применяется для более рационального использования устройств хранения и передачи данных.

Методы сжатия данных можно разделить на два типа:

1. 
   Неискажающие (loseless) методы сжатия (называемые также методами сжатия без потерь) гарантируют, что декодированные данные будут в точности совпадать с исходными;
   
2. 
   Искажающие (lossy) методы сжатия (называемые также методами сжатия с потерями) могут искажать исходные данные, например за счет удаления несущественной части данных, после чего полное восстановление невозможно.
   

Алгоритм Хаффмана

Один из первых алгоритмов эффективного кодирования информации был предложен Д. А. Хаффманом в 1952 году. Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (то есть ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).

1. 
   Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.
   
2. 
   Выбираются два свободных узла дерева с наименьшими весами.
   
3. 
   Создается их родитель с весом, равным их суммарному весу.
   
4. 
   Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.
   
5. 
   Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0. Битовые значения ветвей, исходящих от корня, не зависят от весов потомков.
   
6. 
   Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
   

Допустим, у нас есть следующая таблица частот:



Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n₀ потомков — символы из предыдущего шага и т. д.

Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от листа дерева, соответствующего текущему символу, до его корня, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

Для данной таблицы символов коды Хаффмана будут выглядеть следующим образом: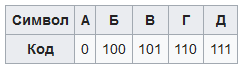