Здравоохранение Динамика. 1. Понятие, формы выражения и виды статистических показателей
 Скачать 85.09 Kb. Скачать 85.09 Kb.
|
|
1.Понятие, формы выражения и виды статистических показателей. Статистический показатель - представляет собой количественную характеристику соц.-эк. явлений и процессов в условиях качественной определенности. Качественная определен ность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью. Все статистические показатели по охвату единиц совокупности разделяются на: индивидуальные; сводные, а по форме выражения на: абсолютные; относительные; средние. Индивидуальные показатели - характеризуют отдельный объект или отдельную совокуп ность - предприятие, банк и т.д. Пример индивидуального абсолютного показателя: оборот тор говой фирмы, совокупный доход домохозяйства и т.д.) На основе соотнесения 2-х индивидуальных абсолютных показателей, характеризующих один и тот же объект или единицу, получают индивидуальный относительный показатель. Сводные показателихарактеризуют группу единиц, представляющую собой часть стати стической совокупности или всю совокупность в целом. Сводные показатели подразделяются на: объемные и расчетные. Объемные показатели получают путем сложения значений признака отдельных единиц совокупности. Различают абсолютные (стоимость основных фондов предприятий отрасли), от носительные (фондовооруженность) и средние (средняя стоимость основных фондов) объемные показатели. Расчетные показатели -вычисляются по различным формулам и служат для решения отдельных статистических задач анализа - измерения вариации, характеристики структурных сдвигов и т.д. Расчет. Показатели также подразделяются на абсолютные, относительные и сред ние. В зависимости от временного фактора различают моментные и интервальные показатели. Статистические показатели, характеризующие соц.-эк. явления и процессы по состоянию на определенный момент времени (на определенную дату, начало и конец месяца, года) назы ваются моментными. Например, численность населения на..., дебиторская задолженность на... Статистические показатели, характеризующие соц.-эк. явления и процессы за определен ный период - день, неделю, месяц, квартал, год - называются интервальными. Например, про изводство продукции, сумма страховых выплат и т.д. 2. Динамический ряд – это ряд чисел, характеризующих изменение явления во времени. Элементы динамического ряда: 1) время (период времени) – интервал или момент (хронологическая дата); 2) уровень ряда , т. е. показатель количества значе ний за периоды времени или какой либо даты. Уровни ряда обозначаются как у0, у1, …, уn. Разли чают крайние уровни ряда (первый и последний) и промежуточные уровни. Динамические ряды классифицируются по различным признакам в зависимости от способов получения. Первичные динамические ряды – это ряды, в которых уровни представлены исходными цифровыми данными, полученными в результате статистического наблюдения. Первичные ряды всегда являются количественными (объем продукции за каждый год). Вторичные (производные) динамические ряды – это ряды, в которых уровни представлены в виде производных величин (средних или относительных показателей), например динамический ряд показателя средней урожайности. В зависимости от признака времени выделяют интервальные и моментные динамические ряды. Моментный динамический ряд – это ряд, уровни которого фиксируют значение изучаемого показателя на определенный момент времени. Интервальный динамический ряд – это ряд, уровни которого характеризуют значение показателя за определенный период времени. Методы вычисления среднего уровня динамического ряда (средней хронологической). С течением времени уровни динамического ряда изменяются, и возникает необходимость обобщающей характеристики развития явления во времени. Эта задача решается с помощью средней величины – среднего уровня ряда, который называется для динамических рядов средней хронологической. Ее рассчитывают для интервальных и моментных рядов. Для интервального ряда средняя хронологическая рассчитывается по формуле: 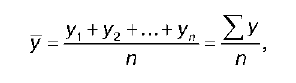 где n – число уровней динамического ряда. Для моментного ряда средняя хронологическая рассчитывается по формуле: 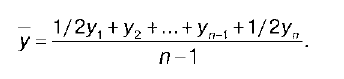 При изучении динамических рядов выделяют две основные задачи: 1) характеристика структуры ряда; 2) прогнозирование будущих уровней временного ряда на основании прошлых и настоящих уровней. Данные, представленные в виде динамических рядов, могут содержать два вида компонентов: 1) систематическая составляющая; 2) случайная составляющая. Систематическая составляющая – это результат воздействия постоянно действующих факторов. Выделяют три основных систематических компоненты динамического ряда: 1) тренд (тенденция) – это систематическая линейная или нелинейная компонента, изменяющаяся во времени; 2) сезонность – это периодические колебания уровней временного ряда внутри года; 3) цикличность – это периодические колебания, вы ходящие за рамки одного года. Промежуток времени между двумя соседними вершинами или впадинами в масштабах года считается длиной цикла. Все три систематические составляющие могут одновременно присутствовать в динамическом ряду. Анализ динамического ряда. Вычисление основных показателей динамического ряда На первом этапе статистической обработки динамических рядов анализируются основные тенденции (тренд) изменения явления во времени. Для этого, во-первых, используются графические изображения, которые часто дают самую исчерпывающую информацию. Во-вторых, вычисляется комплекс специальных показателей, позволяющих дать количественную оценку динамики анализируемого явления. При этом, если полученные показатели дают достаточно ясную и наглядную картину тенденций, то на этом этапе нередко и заканчивается весь анализ динамического ряда. Абсолютный прирост или убыль характеризует изменение явления в единицу времени (за интервал времени). Получается путем вычитания из данных последующего периода данных предыдущего. Если ряд возрастает, то прирост положителен. Если убывает — отрицателен (убыль). Этот показатель не может использоваться при сравнении динамики разнородных данных (вес в кг, рост в см). Кроме того, на его значение оказывает влияние и абсолютный размер анализируемой характеристики. Например: рост в см — трехзначное число, окружность бедра в см — двухзначное. Темп роста или снижения показывает соотношение в процентах последующего уровня и предыдущего, поэтому может использоваться при сравнительном анализе динамики разнородных величин. Получается путем деления последующего уровня на предыдущий и умножения на 100. Если прирост положителен, то показатель больше 100%, если отрицателен — меньше 100%. Темп прироста показывает, на сколько процентов увеличился или уменьшился уровень явления. По существу отражает относительную скорость изменения явления от одного отрезка времени к другому. Вычисляется путем деления абсолютного прироста на предыдущий уровень, либо вычитанием из показателя темпа роста 100. Если прирост положителен — показатель больше 0. Если отрицателен — меньше. Абсолютное значение 1% прироста характеризует значение (стоимость) 1% прироста изучаемого явления. Этот показатель может вычислятьсяделением абсолютного прироста на темп прироста или делением показателя предыдущего уровня на 100. Он является одним из самых существенных, поскольку «размер» одного процента темпа роста и прироста в различных совокупностях может серьезно различаться. Пример: число районов города «N» с высоким уровнем загрязнения атмосферного воздуха в 2001 году было 4, в 2002 стало — 8. Темп роста — 200%. В городе «NN» таких районов в 2001 году было 10, стало — 15. Темп роста — 50%. Однако, в первом случае число неблагополучных районов увеличилось на 4, а во втором — на 5. Даже в одном динамическом ряду значение одного процента роста и темпа прироста может существенно различаться на разных отрезках времени. Показатель наглядности характеризует динамику явления в процентах относительно исходного уровня. Он представляет собой отношение каждого уровня ряда к одному из них (чаще начальному), принятому за 100%. В отличие от предыдущих показателей на всем протяжении временного ряда «стоимость» одного процента этого показателя остается неизменной. Однако, динамика изменения исходных данных от одного промежутка времени к другому становится менее выразительной.
Стандартизация является способом позволяющим устранить влияние структуры (возрастного состава населения: пациентов, исследуемых и т.д.) на итоговые показатели относительных величин. Наиболее распространен метод стандартизации при оценке показателей смертности. Стандартизованный коэффициент смертности разработан для устранения влияния возрастного состава населения и позволяет корректно сравнивать смертность на различных территориях (популяциях). Наиболее часто используется метод прямой стандартизации. St - стандартизованный коэффициент; mх – коэффициент смертности в возрастной группе x изучаемой популяции; nx – численность возрастной группы x в стандартной популяции, n0 – общая численность стандартной популяции. После выбора стандарта численности можно переходить непосредственно к вычислению стандартизованного показателя смертности Ряды динамики 1. Виды рядов динамики и правила их построения 2. Аналитические показатели анализа ряда динамики 3. Приведение рядов динамики к общему основанию. Коэффициенты опережения Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени. Эта задача решается путем построения и анализа рядов динамики. Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени. В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) y. Уровни ряда - это показатели, числовые значения которых составляют динамический ряд. Время - это моменты времени или периоды, к которым относятся уровни. Ряды динамики различаются по следующим признакам. По времени - моментные и интервальные. Моментным называется такой ряд, уровни которого характеризуют состояние явления на определенные даты (моменты времени). Примерами моментных рядов могут быть последовательности показателей численности населения на начало года, величины запаса какого-либо материала на начало периода т. д. Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц). Примером такого ряда могут служить данные о динамике добычи нефти, показателей объема продукции, количества отработанных человеко-дней по отдельным периодам т. д. Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда дает вполне реальный показатель - общий выпуск продукции за год, общие затраты рабочего времени, общий объем продаж акций, объем продаж долларов США на ММВБ и т. д. Сумма же уровней моментного ряда реального содержания, как правило не имеет, т. к. одни и те же единицы совокупности обычно входят в состав нескольких уровней. 2. По форме представления уровней - ряды абсолютных, относительных и средних величин. В приведенных ранее примерах рядов динамики уровни выражены абсолютными величинами. Средними величинами могут выражаться уровни, характеризующие динамику средней реальной заработной платы в промышленности, динамику урожайности зерновых культур, и т. д. Относительными величинами характеризуется, например, динамика доли городского и сельского населения (%) и уровня безработицы. 3. По расстоянию между датами или интервалами времени выделяют ряды с равностоящими и неравностоящими уровнями. Если даты регистрации или окончания периодов следуют друг за другом с равными интервалами, то такие ряды являются равностоящими. Если в рядах динамики прерывающиеся или неравномерные интервалы времени, то такие ряды являются неравностоящими. 4. По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики. Если ведется анализ по времени одного показателя имеем изолированный ряд динамики. Комплексный ряд динамики получаем в том случае, когда в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления. Например, потребление основных продуктов питания на одного члена семьи (кг/ год). При построении динамических рядов необходимо соблюдать определенные правила: 1. Периодизация развития, т.е. расчленение ряда во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. Это, по существу, типологическая группировка во времени. 2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах. Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов. Территориальная и объемная сопоставимость обеспечивается смыканием рядов динамики, при этом либо абсолютные уровни заменяются относительными, либо делается пересчет в условные абсолютные уровни. Не возникает особых сложностей при обеспечении сопоставимости данных по единицам измерения. Стоимостная сравнимость достигается системой сопоставимых цен. Трудности могут появиться при сравнении данных по моменту регистрации. В большей степени это относится к сезонным явлениям. В таких случаях даже регистрации на одну и ту же дату часто бывает недостаточно для обеспечения сопоставимости. Регистрацию таких процессов лучше выполнять в “нейтральные” даты. 3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры. Для стабильных процессов интервалы можно увеличить. Так, переписи населения достаточно проводить один раз в десять лет, учет национального дохода, урожая ведется раз в год, ежедневно регистрируются курсы покупки и продажи валют и т. п. 4. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями. 2. Выравнивание динамических рядов Расчет показателей динамики не дает в полной мере ха рактеристики тенденций развития. Причем, средние показа тели динамики могут дать искаженную картину характера динамики, поскольку они рассчитываются на основе конечно го и начального уровней динамики и не учитывают колебания внутри ряда. Для анализа тенденций развития применяют выравнивание рядов динамики. Наиболее простым способом является сглаживание рядов динамики с помощью средней скользящей. При этом способе вычисляют средний уровень за периоды, сдвигаемые на одну дату. Величина интервала скольжения определяется в зави симости от конкретных особенностей динамики. Он должен быть достаточным для погашения случайных колебаний. Если в колебаниях есть какая-то периодичность, то целесообразно принять его равным периоду этих колебаний. Если нет пери одичности в колебаниях, то следует последовательно укруп нять интервал скольжения, пока не выявится тенденция раз вития. Скользящую среднюю определяют по формулам: …………………………………. где У0, У1, …, Уn уровни ряда; k – интервал скольжения. Сглаживание рядов динамики не всегда четко показывает закономерную тенденцию развития. Для более четкого выяв ления тенденции развития применяют аналитическое вырав нивание рядов динамики, которое позволяет получить уравне ние развития (тренда). Аналитическое выравнивание может производиться несколькими способами: по среднему абсолют ному приросту, с помощью коэффициента роста, способом на именьших квадратов. Выравнивание рядов динамики по среднему абсолютному приросту проводят в случае, если цепные абсолютные прирос ты примерно одинаковы. Уравнение тенденции в этом случае имеет вид: где У0 – начальный уровень; t – порядковый номер даты (t = 1, …, n+1). На графике выровненный ряд имеет форму прямой, соеди няющей начальный и конечный уровни ряда. В случае если стабильными являются коэффициенты роста или темпы прироста, то выравнивание ряда динамики осуществляют по среднему коэффициенту роста: где Выровненный ряд имеет форму показательной кривой, соединяющей начальный и конечный уровни ряда. Недостатком выравнивания динамических рядов по сред нему абсолютному приросту и среднему коэффициенту роста является то, что они не учитывают колебаний внутри ряда. Более эффективным способом выравнивания динамических рядов является применение метода наименьших квадратов. Суть его заключается в подборе уравнения, которое наиболее точно отражало бы тенденцию развития. Подробно метод наименьших квадратов рассмотрен в теме «Корреляционный анализ». При выравнивании динамического ряда методом наимень ших квадратов находят уравнение зависимости уровней ряда от времени. Выравнивание может производиться с помощью различных функций: линейной, параболической, гиперболиче ской, показательной и других. Выбор функций чаще всего осу ществляют по графику исходного ряда. В случае сильных коле баний целесообразно использовать график скользящей сред ней. Существенную помощь оказывает также анализ цепных абсолютных приростов и коэффициентов роста. Например, если цепные абсолютные приросты относительно стабильны, то в качестве уравнения тренда может быть принято уравнение прямой линии Оценку полученного уравнения также как и при парной корреляции производят с помощью коэффициента или индек са корреляции, который показывает тесноту связи между ис ходными и выровненными уровнями динамического ряда. Чем ближе коэффициент или индекс корреляции к 1, тем в боль шей степени уравнение тренда отражает тенденцию развития. 2. Абсолютные показатели. Исходной, первичной формой выражения статистических показателей являются абсолют ные величины.Статистические показатели в форме абсолютных величин характеризуют абсо лютные размеры изучаемых статистических процессов и явлений, их массу, площадь, объем и т.д. Абсолютные статистические показатели всегда являются именованными числами. Они выражаются в натуральных, стоимостных и трудовых единицах измерения В международной практике используются такие натуральные единицы измерения: тонны; килограммы; метры; кв. м, куб. м; км; шт.; литры и т.д. Условно-натуральныепоказатели используются, когда какой-либо продукт имеет не сколько разновидностей, и общий объем можно определить исходя из общего для всех разно видностей потребительского свойства. (Например, различные виды органического топлива пе реводят в условное топливо с теплотой сгорания 29,3 МДж/г, (7000 Ккал/кг). В отдельных случаях для измерения используется произведение двух единиц. Например, производство электроэнергии, измеряемое в киловатт-часах и т.д. В условиях рыночной экономики наибольшее применение имеют стоимостные единицы измерения,дающие денежную оценку соц.-эк. явлениям и процессам. (ВВП) К трудовым единицам измерения,позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы. 3. Относительные показатели. Относительный показательпредставляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками соц.-эк. процессов и явлений. При расчете относительного показателя абсолютный показатель, находящийся в числите ле, называется текущим (сравниваемым), а показатель, который находится в знаменателе - ос нованием или базой. Относительные показатели могут выражаться в коэффициентах, процентах или быть име нованными. Относительные показатели можно разделить на следующие виды: динамики, плана, структуры, координации, интенсивности развития, сравнения. 1) Относительный показатель динамики (ОПД)- это отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом.  ОПД показывает во сколько раз текущий уровень превышает предшествующий или какую до лю от последнего составляет. Если данный показатель выражен кратным отношением, он назы вается коэффициентом роста, при домножении этого коэффициента на 100% получают темп роста. 2) Относительный показатель плана (ОПП)используется предприятиями с целью пер спективного планирования своей деятельности. 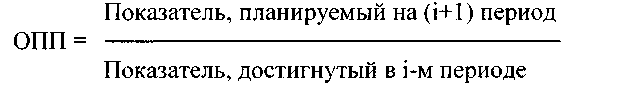 3) Относительный показатель структуры (ОПС)представляет собой соотношение структурных частей изучаемого объекта и их целого. 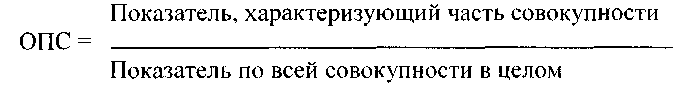 ОПС выражается в долях единицы или в % - х. Таблица Структура внешнеторгового оборота в 1997г.
Рассчитанные в графе 2 проценты представляют собой относительные показатели структуры. Сумма всех удельных весов всегда должна быть строго равна 100%. 4) Относительный показатель координации (ОПК) —характеризует соотношение отдельных частей целого между собой. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной. В результате получают, сколько единиц каждой структурной части приходится на 1 единицу (иногда на 100, 1000 и т.д. единиц) базисной структурной части. (Из табл. видно, что на каждый триллион рублей импорта приходилось 1,29 трлн. руб. экспорта (505,6 /391,1)). Относительный показатель интенсивности (ОПИ) - характеризует степень распро странения изучаемого процесса или явления в присущей ему среде:  ОПИ исчисляется, когда абсолютная величина оказывается недостаточной для формули ровки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Он может выражаться в %, быть именованной величиной. 5) Относительный показатель сравнения (ОПСр)- представляет собой соотношение од ноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области и т.п.)  4.Графики в статистике Статистический график - это чертеж, на котором статистические совокупности, харак теризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Под основой графика (графический образ)понимают геометрические знаки, т.е. сово купность точек, линий фигур, с помощью которых изображаются статистические показатели. Поле графика -это часть плоскости, где расположены графические образы. Поле графи ка имеет определенные размеры, которые зависят от его назначения. Пространственные ориентирыграфика задаются в виде системы координат. Система координат необходима для размещения геометрических знаков в поле графика. Наиболее рас пространенной является система прямоугольных координат. Масштабные ориентирыстатистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика - это мера перевода числовой величины в графическую. Шкала включает три элемента: линию (носитель шкалы), определенное число помеченных черточками точек, цифровое обозначение чисел. По правилам числовое значение необходимо помещать строго против соответствующих точек. (см. рис.)  Различают шкалы прямолинейные (миллиметровая линейка) и криволинейные - дуговые и круговые (циферблат часов). Различают также шкалы равномерные и неравномерные. Шкала является равномерной, если равным графическим отрезкам соответствуют равные числовые величины. Неравномер ным шкалам соответствуют неравные числовые значения. Экспликация графика- это пояснение его содержания, включает в себя заголовок графи ка, объяснения масштабных шкал, пояснения отдельных элементов графического образа. Вида статистических графиков. |
