1. Понятие о статистике 3

• Название: 1. Понятие о статистике 3
• Дата: 20.12.2022
• Размер: 4.08 Mb.
• Имя файла: TEORIYA_STATISTIKI_-_lekcii.doc
• Тип: Документы; #853901
• страница: 9 из 43

3.3. Расчет показателей размера и интенсивности вариации

Простейшим показателем является размах вариации – абсолютная разность между максимальным и минимальным значениями признака из имеющихся в изучаемой совокупности значений (24):

. (24)

Поскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измерять закономерную силу его вариации во всей совокупности. Предназначенный для данной цели показатель должен учитывать и обобщать все различия значений признака в совокупности без исключения. Число таких различий равно числу сочетаний по два из всех единиц совокупности (в нашем примере про ВО число сочетаний составит ). Однако нет необходимости рассматривать, вычислять и осреднять все отклонения. Проще использовать среднюю из отклонений отдельных значений признака от среднего арифметического значения признака, а таковых в нашем примере про ВО всего 35. Но среднее отклонение значений признака от средней арифметической величины согласно первому свойству последней равно нулю. Поэтому показателем силы вариации выступает не арифметическая средняя отклонений, а средний модуль отклонений, или среднее линейное отклонение (25):

. (25)

В нашем примере про ВО по данным табл. 12 среднее линейное отклонение вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины (расчет числителя произведен в 7-м столбце табл. 12), т.е. по формуле (26):

(млн.долл.). (26)

Это означает, что в среднем величина ВО в изучаемой совокупности таможенных постов отклонялась от средней величины ВО в РФ на 14,678 млн.долл.

Простота расчета и интерпретации составляют положительные стороны показателя Л, однако математические свойства модулей «плохие»: их нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением, параметром которого является не средний модуль отклонений, а среднее квадратическое отклонение, обозначаемое малой греческой буквой сигма ( 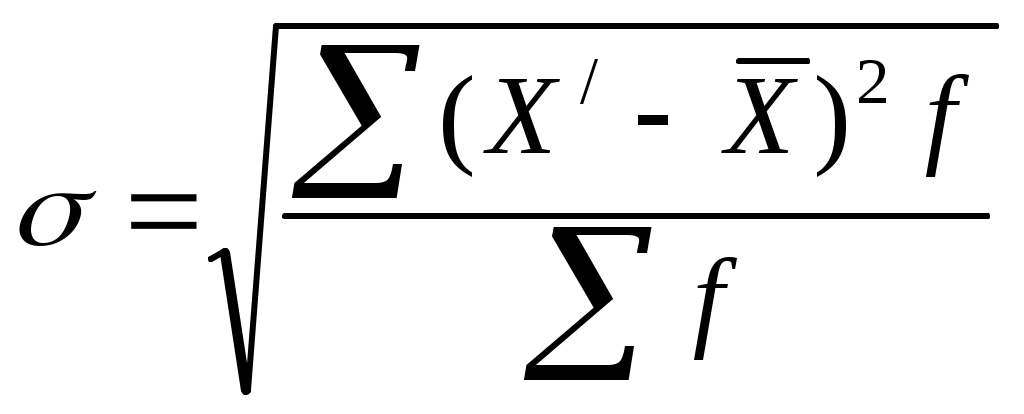) или s и вычисляемое по формуле (27) – для ранжированного ряда и по формуле (28) – для интервального ряда:

; (27) . (28)

В нашем примере про ВО по данным табл. 12 среднее квадратическое отклонение величины ВО по формуле (28) составило (расчет числителя произведен в 8-м столбце табл. 12):

(млн.долл.).

Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего модуля отклонений. Разница между ними тем больше, чем больше в изучаемой совокупности резких, выделяющихся отклонений, что служит индикатором «засоренности» совокупности неоднородными с основной массой элементами. Для нормального закона распределения отношение . В нашем примере про ВО: , т.е. в изучаемой совокупности наблюдаются некоторое число таможенных постов с отличающимися от основной массы величинами ВО.

Квадрат среднего квадратического отклонения представляет собой дисперсию отклонений, на использовании которой основаны практически все методы математической статистики, ее формула имеет вид (29) – для несгруппированных данных (простая дисперсия) и (30) – для сгруппированных (взвешенная дисперсия):

; (29) . (30)

Еще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь в ее центральной части, служит среднее квартильное расстояние (отклонение), т.е. средняя величина разности между квартилями, определяемая по формуле (31):

. (31)

В нашем примере про ВО по формуле (31): (млн.долл.).

Сила вариации в центральной части совокупности, как правило, меньше, чем в целом по всей совокупности. Соотношение между средним линейным отклонением и средним квартильным расстоянием служит для изучения структуры вариации: большое значение такого соотношения свидетельствует о наличии слабоварьирующего «ядра» и сильно рассеянного вокруг него окружения в изучаемой совокупности. Для нашего примера про ВО соотношение Л/q = 1,021, что говорит о совсем незначительном различии силы вариации в центральной части совокупности и на ее периферии.

Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков необходимы относительные показатели вариации, которые вычисляются как отношение абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака, то есть показатели (32) – (35):

• 
  относительный размах вариации: ; (32)
  
• 
  линейный коэффициент вариации: ; (33)
  
• 
  квадратический коэффициент вариации: ; (34)
  
• 
  относительное квартильное расстояние: . (35)
  

В нашем примере про ВО эти показатели составляют:

= 87/60,82 =1,43, или 143%; = 14,678/60,82 = 0,241, или 24,1%;

= 19,756/60,82 = 0,32, или 32%; d = 14,38/60,82 = 0,236, или 23,6%.

Оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава, она состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив¹⁹. Так, для совокупности таможенных постов вариация величины ВО может быть определена как слабая, если < 25%, умеренная при 25% < < 50% и сильная при > 50%.

Различная сила, интенсивность вариации обусловлены объективными причинами, поэтому нельзя говорить о каком-либо универсальном критерии вариации (например, 33%), так как для разных явлений и признаков этот критерий различен²⁰.