Практикум по Электротехника и электроника. 1 Последовательное соединение в цепи синусоидального тока
 Скачать 379.5 Kb. Скачать 379.5 Kb.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица 1.2 | |||||||
| Вариант | R1, Ом | R2, Ом | XL2, Ом | R3, Ом | XC3, Ом | XC4, Ом | U, В |
| 1 | 5 | 3 | 4 | 16 | 12 | 25 | 100 |
| 2 | 10 | 8 | 6 | 16 | 12 | 20 | 100 |
| 3 | 16,7 | 6 | 8 | 12 | 16 | 16,7 | 100 |
| 4 | 20 | 16 | 12 | 4 | 3 | 10 | 100 |
| 5 | 25 | 12 | 16 | 3 | 4 | 25 | 100 |
| 6 | 5 | 12 | 16 | 4 | 3 | 20 | 100 |
| 7 | 10 | 16 | 12 | 3 | 4 | 16,7 | 100 |
| 8 | 16,7 | 6 | 8 | 16 | 12 | 10 | 100 |
| 9 | 20 | 8 | 6 | 6 | 8 | 5 | 100 |
| 10 | 25 | 3 | 4 | 6 | 8 | 5 | 100 |
| 11 | 5 | 4 | 3 | 16 | 12 | 10 | 100 |
| 12 | 10 | 4 | 3 | 12 | 16 | 16,7 | 100 |
| 13 | 16,7 | 3 | 4 | 8 | 6 | 20 | 100 |
| 14 | 20 | 8 | 6 | 4 | 3 | 25 | 100 |
| 15 | 25 | 6 | 8 | 12 | 16 | 25 | 100 |
| 16 | 5 | 16 | 12 | 8 | 6 | 20 | 100 |
| 17 | 10 | 16 | 12 | 6 | 8 | 16,7 | 100 |
| 18 | 16,7 | 12 | 16 | 3 | 4 | 10 | 100 |
| 19 | 20 | 12 | 16 | 6 | 8 | 10 | 100 |
| 20 | 25 | 6 | 8 | 3 | 4 | 5 | 100 |
| 21 | 10 | 6 | 8 | 12 | 16 | 10 | 100 |
| 22 | 16,7 | 16 | 12 | 16 | 3 | 5 | 100 |
| 23 | 20 | 12 | 6 | 4 | 8 | 15 | 100 |
| 24 | 25 | 8 | 6 | 3 | 4 | 20 | 100 |
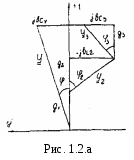
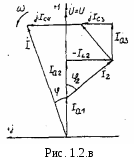
Первоначально откладывают в масштабе (mu) комплекс напряжений Ů = U (ψu=0) в положительном направлении оси вещественных чисел, затем (например для векторной диаграммы токов), откладывают в масштабе (mi) токи Ia1, Ia2, -jIL2, Ia3, +jIC4. Полный ток цепи (замыкающий вектор) отстает по фазе от напряжения при bL2 > (bС3+bС4) (φ>0) и опережает по фазе напряжение при bL2 < (bС3+bС4) (φ<0)
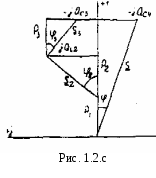
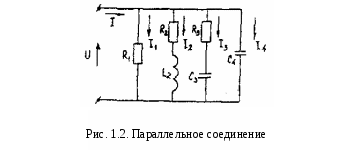
На рис. 1.2,а, рис. 1.2,в, рис. 1.2,с построенных, соответственно, диаграмма проводимостей, векторная диаграмма токов и диаграмма мощностей для произвольно принятых значений проводимостей цепи.

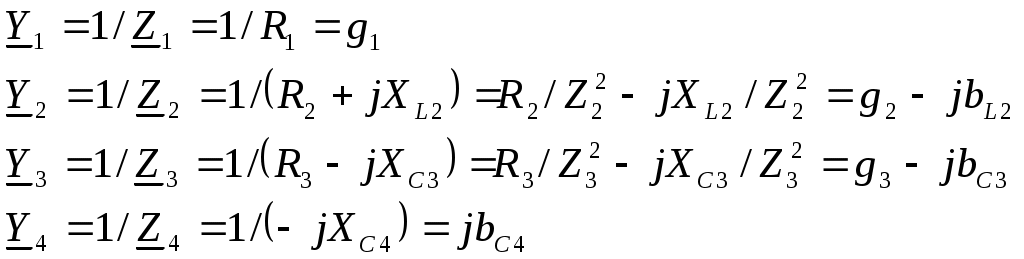 (1.6)
(1.6)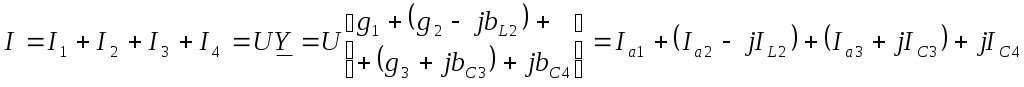 (1.8)
(1.8)