практичне. ПРАКТИЧНЕ ЗАНЯТТЯ-1 (2). 1 практичне заняття 1
 Скачать 122.54 Kb. Скачать 122.54 Kb.
|
|
Приклад 16. В ящику 10 червоних і 6 синіх ґудзиків. Навмання виймають два ґудзики. Визначити ймовірність того, що ґудзики будуть одного кольору. Розв’язання. Нехай подія А – ґудзики одного кольору, подія В – ґудзики червоні, подія С – ґудзики сині. Очевидно, 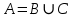 і події В і С несумісні, тому за теоремою P(A) = P(B) + P(C). Знайдемо P(B) та P(C): 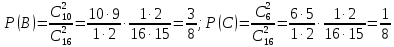 Отже, 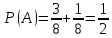 Відповідь. 1/2 Приклад 17. Для виконання завдання замовник звернувся до двох виконавців. Ймовірність того, що перший виконавець дасть згоду виконати замовлення дорівнює 0,8, а другий — 0,9. Знайти ймовірність того, що замовлення буде прийнято принаймні одним з цих виконавців. Розв’язання. Позначимо події: A = «завдання прийнято для виконання»; A1 = «перший виконавець дав згоду виконати завдання»; A2 = «другий виконавець дав згоду виконати завдання». Тоді A=A1+A2 Оскільки згода виконати замовлення першим виконавцем не виключає згоди виконання замовлення другим, події сумісні. Тоді 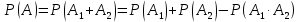 Події A1 та A2 доцільно вважати незалежними, тому що ймовірність згоди кожного виконавця не залежить від того, чи дав згоду інший виконавець. Тому 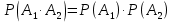 Отже, 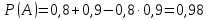 Відповідь. 0,98 Приклад 18. На відрізок [0,1] випадковим чином кидається точка. Визначити ймовірність події С: «точка потрапить в інтервал 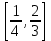 або в інтервал або в інтервал 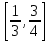 ». ».Розв’язання. Подія С є об'єднанням подій «точка потрапить в інтервал 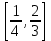 » (подія А) і «точка потрапить в інтервал » (подія А) і «точка потрапить в інтервал 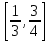 » (подія В). » (подія В).Ці події сумісні – їх перетином є подія D: «точка потрапить в інтервал 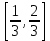 ». ».Ймовірності подій A, B, 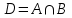 відповідно рівні відповідно рівні 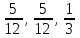 . Звідси за формулою для ймовірності події З маємо: . Звідси за формулою для ймовірності події З маємо: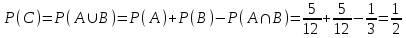 Відповідь: 0,5 Приклад 19. У цеху є три агрегати. Зупинка цеху (відмова) настає, якщо відмовили обидва агрегату з номерами 1 і 2 або один 3-й агрегат. Необхідно знайти ймовірність відмови цеху. Розв’язання. Подію А (відмова цеху), можна представити у вигляді 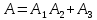 де події A1, А2, А3 – позначають відповідно відмови першого, другого і третього агрегатів. У цьому випадку ймовірність події А дорівнює: 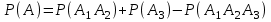 Так як за умовою завдання, події A1, А2, А3 є незалежними (в сукупності), то: 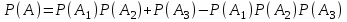 1.3 Завдання для самостійної роботи Завдання 1. Класичне означення ймовірності 1. Серед 25 фірм, з яких 10 українських, а інші російські, розігрується 5 урядових контрактів. Вважається, що кожна фірма має рівні шанси на отримання контракту. Знайти ймовірність того, що принаймні дві українські фірми виграють контракт. 2. У фірмі 10 співробітників (6 чоловіків і 4 жінки) претендують на заміщення трьох вакансій. Вважають, що всі кандидатури мають рівні шанси на зайняття цих вакансій. Знайти ймовірність того, що жінки не займуть жодної вакансії. 3. У групі з 12 бізнесменів тільки 8 мають досвід роботи у запропонованій новій галузі. Для проекту потрібно відібрати 4 особи. За припущення, що відбір претендентів проводять навмання, знайти ймовірність того, що в команду з чотирьох чоловік потраплять всі, хто має досвід роботи. 4. Комплект містить 7 виробів першого сорту, 6 – другого сорту і 2 вироби – третього сорту. Навмання обирають 5 виробів. Знайти ймовірність того, що серед них не виявиться виробів третього сорту. 5. Із 15 рейсів, що виконуються з аеропорту протягом доби, 60 % рейсів виконуються на власному літаковому парку. Знайти ймовірність того, що з вибраних навмання 5 рейсів рівно 3 виконуються на власному парку. 6. 12 виробів, серед яких 4 нестандартних, випадковим способом розбиваються на дві рівні партії. Знайти ймовірності того, що: а) у кожній партії буде рівна кількість нестандартних виробів; б) усі нестандартні вироби будуть в одній партії. 7. У конкурсі газети бере участь 12 чоловіків та 8 жінок. Є два призових місця. За припущення, що відбір претендентів ведуть навмання, яка ймовірність того, що обидва місця займуть жінки? 8. З 10 літаків, що прибувають в аеропорт протягом доби, 80 % мають повне комерційне завантаження. Знайти ймовірність того, що серед п’яти випадковим способом узятих літаків тільки 4 мають повне завантаження. 9. В авіакасі було 15 квитків, серед яких 6 квитків до пункту А. До кінця зміни продано 8 квитків. Знайти ймовірність того, що в касі не залишилося квитків до пункту А, якщо ймовірність продажу кожного квитка однакова. 10. Партія з 30 виробів містить 10 % браку. Знайти ймовірність того, що серед 7 виробів, узятих випадково: а) тільки 2 бракованих; б) жодного бракованого. 11. Комплект складається із восьми різних виробів, з яких 3 вироби коштують по 4 грн, ще 3 – по 5 грн і 2 – по 3 грн. Знайти ймовірність того, що взяті навмання 2 вироби коштують 7 грн. 12. У групі 10 хлопців і 5 дівчат, серед яких вибирають дві особи для участі у конференції. Яка ймовірність того, що: а) виберуть двох хлопців; б) виберуть хлопця й дівчину? 13. У деканаті знаходяться 10 студентських книжок. Шестеро студентів, які зайшли до деканату, навмання беруть по 1 студентській книжці. Яка ймовірність того, що: а) усі студенти взяли свої студентські книжки; б) 4 студента взяли свої студентські книжки? 14. В класі навчається 32 учні серед яких 17 – з блакитними очима, 12 – з сірими, а інші – з карими. Навмання вибирають учня і визначають колір його очей. Яка ймовірність того, що учень не з блакитними очима? 15. Знайти ймовірність того, що вибране навмання двозначне число не є кратним 10. 16. З відривного календаря навмання відривають листок. Яка ймовірність того, що число, яке написане на відірваному листку, дорівнює 29, якщо у році 365 днів? 17. В урні 30 куль: 10 червоних, 5 синіх в 15 білих. Витягується одна куля. Знайти ймовірність появи кольорового кулі. 18. У збірнику білетів з математики всього 25 білетів, в 10 з них зустрічається питання з похідної. Знайдіть ймовірність того, що в випадково обраному на іспиті білету учневі дістанеться питання з похідної. 19. У магазин надійшло 30 холодильників, п'ять з яких мають заводський дефект. Випадковим чином вибирають один холодильник. Яка ймовірність того, що він буде без дефекту? 20. Набираючи номер телефону, абонент забув дві останні цифри, але пам'ятає, що одна з них – нуль, а інша – непарна. Знайти ймовірність того, що він набере правильний номер. 21. Абонент забув пін-код до своєї сім-карті, проте пам'ятає, що він містить три «п'ятірки», а одна з цифр – чи то «сімка», чи то «вісімка». Яка ймовірність успішної авторизації з першої спроби? 22. У ліфт 20-поверхового будинку на першому поверсі зайшли 3 людини. І поїхали. Знайти ймовірність того, що: а) вони вийдуть на різних поверхах б) двоє вийдуть на одному поверсі; 23. На семимісну лавку випадковим чином розсідається 7 осіб. Яка ймовірність того, що дві певних людини виявляться поруч? 24. На шахову дошку з 64 клітин ставлять навмання дві тури, білого і чорного кольору. З якою ймовірністю вони не будуть «бити» одна одну? 25. Студент знає відповіді на 25 екзаменаційних питань з 60. Яка ймовірність здати іспит, якщо для цього треба було б відповісти не менше ніж на два з трьох питань? Завдання 2. Статистичні та геометричні ймовірності 1. До авіакаси у випадковий час у межах 10 хв звернулось 2 пасажири. Обслуговування одного пасажира триває 2 хв. Знайти ймовірність того, що пасажир, який звернувся другим, буде вимушений зачекати. 2. Відділ технічного контролю видавництва виявив 5 бракованих книжок у партії з випадково відібраних 250 книжок. Знайти відносну частоту виявлення бракованих книжок. 3. Два літаки прибувають у зону аеропорту у випадковий час між 12:00 і 12:30. Знайти ймовірність того, що літак, який прибув другим, не буде вимушений чекати дозволу на посадку, якщо чергову посадку можна здійснювати не раніше, ніж за 10 хв після попередньої. 4. У рівнобедреному трикутнику з бічною стороною 5 см та кутом при вершині 120° довільно розміщено квадрат зі стороною 1,5 см. Знайти ймовірність того, що навмання вибрана точка трикутника лежатиме в квадраті. 5. На відрізку довжиною 15 см випадково поставлено дві точки. Знайти ймовірність того, що відстань між цими точками не перевищує 7 см. 6. Відстань між пунктами M і N літак долає за 1 год, а потяг – за 18 год. Потяг у випадковий час протягом доби вирушає з пункту M до N. Знайти ймовірність того, що черговий літак прибуде до пункту N раніше від потяга, якщо між M і N виконується за розкладом один рейс літака щодоби. 7. У ромбі зі стороною 5 см та гострим кутом 60 ° лежить прямокутник зі сторонами 2 та 3 см. Знайти ймовірність того, що навмання вибрана у ромбі точка лежатиме і в прямокутнику. 8. З проміжку [0,1] випадковим способом вибирають два дійсних числа. Знайти ймовірність того, що їх сума не більша одиниці, а добуток не перевищує 2/9. 9. Кожне з двох дійсних додатних чисел не більше 4. Знайти ймовірність того, що їх добуток також буде не більше 4. 10. Усередині кола радіусом 5 мм розташовано прямокутник зі сторонами 4 та 6 мм. Знайти ймовірність того, що навмання вибрана у колі точка лежатиме і в прямокутнику. 11. Метрову стрічку випадковим чином розрізають ножицями. Знайти ймовірність того, що довжина обрізка складе не менше 80 см. 12. У трикутник зі сторонами а=9, b=13, c=16 вписаний коло. Точка M довільно ставиться в трикутник. Знайти ймовірність того, що точка потрапить в коло. Нагадую, що вписане коло лежить всередині трикутника і дотичне до його сторін в 3 точках. 13. У колі радіуса 10 см знаходиться прямокутний трикутник з катетами 12 і 7 см. В коло навмання ставиться крапка. Знайти ймовірність того, що вона не потрапить в даний трикутник. 14. Дві вантажні машини можуть підійти на навантаження в проміжок часу від 19:00 до 20:30. Навантаження першої машини триває 10 хвилин, другої - 15 хвилин. Яка ймовірність того, що одній машині доведеться чекати закінчення навантаження іншої? 15. Студенти випадковим чином приходять в їдальню з 14:00 до 15:00, при цьому обід кожного з них займає приблизно 20 хвилин. Знайти ймовірність того, що: а) Коля зустрінеться з Олею під час обіду, б) дана зустріч не відбудеться. 16. У квадрат з вершинами (0;0), (1;0), (1;1), (0;1) навмання кинута точка. Знайдіть ймовірність того, що координати цієї точки задовольняють нерівності y<2x. 17. Загадуються два числа x і y в проміжку від 0 до 5. Яка ймовірність, що xy>2? 18. На площині проведено паралельні прямі на відстані 15 см одна від одної. На площину кидають монету діаметром 5 см. Знайти ймовірність того, що монета перетне одну із паралельних прямих. 19. У круг навмання кинуто точку. Яка ймовірність того, що вона потрапить у квадрат, вписаний у круг? 20. При перевірці готової продукції було виявлено 7 бракованих одиниць товару із 140 перевірених. Знайти відносну частоту бракованих одиниць товару. 21. При стрільбі по мішені було виявлено, що відносна частота влучень дорівнює 0,9. Проведено 70 пострілів. Скільки пострілів були влучними? 22. Студент і студентка домовились зустрітись в певному місці між 19 та 20 год. Якщо студент приходить перший, він чекає студентку 30 хв і йде з місця зустрічі. Якщо першою прийде студентка, вона чекає студента 10 хв і йде з місця зустрічі. Знайти ймовірність того, що зустріч відбудеться. 23. Абонент протягом години чекає телефонного дзвінка. Яка ймовірність того, що йому зателефонують протягом перших 15 хв? 24. Дві особи домовилися зустрітися в певному місці між 12 і 13 год., Причому кожен, хто прийде на зустріч чекає іншого протягом 20 хв., але не довше, ніж до 13.00, після чого йде. Знайти ймовірність зустрічі цих осіб, якщо кожен з них приходить в випадковий момент часу, не узгоджений з моментом приходу іншого. 25. Два дійсних числа випадковим чином вибирають з інтервалу [0; 5]. Яка ймовірність того, що: а) сума двох чисел менше 4; б) добуток двох чисел більше 5. Завдання 3. Ймовірності суми та добутку подій 1. Фірма має можливість отримати два контракти. Ймовірність отримання першого контракту дорівнює 0,9, а другого – 0,8. Вважаючи ці події незалежними, знайти ймовірності подій: а) фірма отримає обидва контракти; б) фірма отримає принаймні один контракт. 2. Надійність лінії зв’язку між об’єктами (ймовірність безвідмовної роботи протягом певного часу) дорівнює 0,75. Для підвищення якості зв’язку встановлено резервну лінію надійністю 0,65. Визначити надійність зв’язку з резервною лінією. 3. Через метеорологічні умови літак було відправлено на запасний аеродром, під час наближення до якого у баках літака залишалося палива на 3 заходи на посадку. Ймовірність посадки літака за першого заходу дорівнює 0,8, за другого – 0,95, за третього – 0,995. Знайти ймовірність вдалої посадки літака. 4. Є 8 кандидатів на отримання роботи. Серед них є люди з відповідною кваліфікацією (подія А) і люди, що закінчили Видавничо-поліграфічний інститут (подія В), та інші. Їх кількості подано в таблиці 2. Таблиця 2 – Данні для задачі 4
Усі кандидати мають рівні шанси на отримання роботи. Знайти ймовірність того, що роботу отримає людина без кваліфікації, або яка закінчила Видавничо-поліграфічний інститут. 5. Імовірність виготовлення виробу вищого сорту на першому верстаті становить 0,7, на другому – 0,8. На першому верстаті виготовлено 2 вироби, на другому – 3. Знайти ймовірність того, що всі вироби належать до вищого сорту. 6. Відомо, що в деякому регіоні 40 % компаній мають у штаті юриста і 80 % компаній мають у штаті економіста. Вважаємо, що ці дві події незалежні. Знайти ймовірність того, що фірма має в штаті економіста і юриста. 7. Є два ринки цінних паперів. Інвестиційна фірма направила на обидва ринки водночас 260 акцій різноманітної якості. У визначений день на першому ринку зросли ціни 197 акцій (подія А), а на другому ринку зросли ціни 191 акції (подія В). Одночасно на обох ринках зросли ціни 165 акцій. Інші акції не піднялися в ціні. Результати торгів наведено в таблиці 3. Таблиця 3 – Данні для задачі 7
Заповнити порожні місця в таблиці. Знайти ймовірність того, що зросла ціна акцій на першому ринку, якщо відомо, що зросла ціна акцій на другому ринку. 8. На фірмі опитано 100 службовців із метою вивчення стану транспортного обслуговування. Виявилося, що 70 осіб користуються метро (подія А). Іншими видами транспорту користуються 40 осіб (подія В), а 20 осіб одночасно користуються метро та іншими видами транспорту. Опитування занесено в таблицю 4. Таблиця 4 – Данні для задачі 8
Заповнити порожні місця в таблиці. Знайти ймовірність того, що службовець користується метро або іншими видами транспорту. 9. Радіостанція аеропорту надсилає 3 повідомлення для літака. Імовірність підслуховування розвідувальним агентством першого повідомлення дорівнює 0,6; другого – 0,65; третього – 0,7. Знайти ймовірність того, що агентство підслухало: а) тільки два повідомлення; б) усі три повідомлення. 10. З опитаних бізнесменів 80 % віддають перевагу зберіганню грошей у банку (подія А), 60 % вкладає гроші в цінні папери (подія В), 50 % одночасно тримають гроші в банку та вкладають у цінні папери. Результати опитування подано в таблиці 5. Таблиця 5 – Данні для задачі 10
Заповнити таблицю до кінця. Знайти ймовірність того, що навмання обраний бізнесмен тримає гроші в банку або у вигляді цінних паперів. 11. Мішень складається з трьох областей, які попарно не перетинаються. Ймовірність влучення стрільцем у першу область мішені дорівнює 0,45, у другу область – 0, 35, а у третю – 0, 15. Яка ймовірність того, що при одному пострілі стрілець влучить: а) у першу або в другу область; б) не влучить у мішень? 12. Для виконання завдання замовник звернувся до двох виконавців. Ймовірність того, що перший виконавець надасть згоду виконати замовлення дорівнює 0,8, а другий – 0,9. Знайти ймовірність того, що замовлення буде прийнято принаймні одним з цих виконавців. 13. Три стрільці незалежно один від одного стріляють по мішені. Ймовірність влучення в мішень для першого дорівнює 0,7, для другого – 0,8, для третього – 0,9. Яка ймовірність, що: а) хоча б один з них влучить у мішень; б) тільки двоє влучать у мішень. 14. У першій урні міститься 7 білих і 3 чорних кульки; у другій – 5 білих і 5 чорних кульок; у третій – 4 білих і 6 чорних кульок. З кожної урни навмання виймають по одній кульці. Знайти класичну ймовірність того, що серед вибраних кульок виявляться: а) лише одна біла кулька; б) дві білі кульки. 15. Перший стрілець влучає у ціль з ймовірністю 0,8, другий – з ймовірністю 0,9, а третій – з ймовірністю 0,85. Яка ймовірність того, що хоча б один стрілець влучить у ціль? 16. Робітник обслуговує одночасно 3 верстати. Ймовірність порушення роботи протягом години для першого дорівнює 0,1, для другого – 0,2, для третього – 0,2. Яка ймовірність того, що: а) усі три верстати працюватимуть протягом години; б) хоча б один із них вийде з ладу? 17. В деякому класі ймовірність обрати відмінника становить 0,1, а учня, що навчається на «добре і відмінно», – 0,4. Знайти ймовірність того, що обраний учень навчається без оцінок «задовільно» і «незадовільно». 18. Двоє стрільців виконали по одному пострілу у мішень. Ймовірність влучення для першого стрільця становить 0,7, а для другого – 0,8. Яка ймовірність того, що не відбудеться жодного влучення? 19. Знайти ймовірність того, що навмання вибране двозначне число ділиться на 5 і на 10. 20. Знайти ймовірність того, що навмання вибране двозначне число ділиться на 5 або на 10. 21. В першому класі кожен третій учень має блакитні очі, в другому класі – кожен четвертий, а в третьому – половина дітей має блакитні очі. З кожного класу навмання обирають по одній дитині. Яка ймовірність того, що всі три обрані дитини мають блакитні очі? 22. В комплекті з 10 м’ячів є 7 нових і 3, якими вже грали. Для першої партії навмання взяли 1 м’яч, для другої – 2 м’ячі. М’ячі після першої і другої партії назад не повертались. Яка ймовірність взяти новий м’яч для третьої партії? 23. Магазин отримав продукцію в ящиках з чотирьох оптових складів: чотири з 1-го, п'ять з 2-го, сім з 3-го і чотири з 4-го. Випадковим чином обраний ящик для продажу. Яка ймовірність того, що це буде ящик з першого або третього складу. 24. У кожному з трьох ящиків є по 10 деталей. У першому ящику 8 стандартних деталей, в другому – 7, в третьому – 9. З кожного ящика навмання витягують по одній деталі. Знайти ймовірність того, що всі деталі виявляться стандартними. 25. У трьох урнах є по 6 білих і по 4 чорних кулі. З кожної урни витягують навмання по одній кулі. Знайти ймовірність того, що: а) всі три кулі будуть білими; б) всі три кулі будуть одного кольору. 1.4 Питання для самоконтролю 1. Що таке n!? 2. Як обчислити кількість перестановок з n елементів? 3. Як обчислити кількість розміщень з n по m елементів? 4. Як обчислити кількість сполучень з n по m елементів? 5. Якими співвідношеннями пов’язані перестановка, розміщення, сполучення? 6. Продовжить формули. P (A1 + A2) = P (A1 – A2) = P (A1 + A2 + A3) = 7. Що називають умовною ймовірністю події A за умови появи події B? 8. Які дві події називають незалежними? 9. Які три події називають незалежними? 10. Які чотири події називають незалежними? 11. Поясніть на прикладі попарну незалежність і незалежність у сукупності? 12. Чи можуть бути події попарно незалежні і при цьому залежні у сукупності? Наведіть приклад. 13. Відомо, що P (A1 + A2) = P (A1 – A2). Чому дорівнює P (A1A2), P (A2), P (A1)? 14. Для даного ймовірнісного простору скільки ймовірностей має подія A? А умовних ймовірностей? 15. Що можна сказати про незалежність подій A і B, якщо 1) P (B) = 0; 2) P (B) = 1? 1.5 Тренувальний тест до практичного заняття 1 Рівень 1 Оберіть одну з відповідей 1.Кількість сполучень з n елементів по k (k≤n) обчислюють за формулою: а) 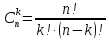 ; б) ; б) 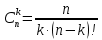 ; в) ; в) 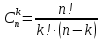 ; г) ваш варіант формули. ; г) ваш варіант формули.2. Для несумісних подій Ата В виконується рівність: а) Р(А+В)=Р(А)+Р(В); б) Р(А+В)=Р(А)·Р(В); в) Р(А+В)=Р(А)+Р(В) – Р(А·В); г) ваш варіант формули. 3. Для незалежних подій А та В виконується рівність: а) Р(А·В)=Р(А)+Р(В); б) Р(А·В)=Р(А)·Р(В) – Р(А·В); в) Р(А·В)=Р(А)·Р(В); г) ваш варіант формули. 4. Кількість розміщень з повторенням n елементів по k обчислюють за формулою: а) 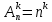 ; б) ; б) 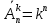 ; в) ; в) 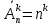 ; г) ваш варіант формули. ; г) ваш варіант формули.5. Для сумісних подій Ата В виконується рівність: а) Р(А+В)=Р(А)+Р(В); б) Р(А+В)=Р(А)·Р(В); в) Р(А+В)=Р(А)+Р(В) – Р(А·В); г) ваш варіант формули. Рівень 2 Знайдіть розв’язання задач 1. Скільки різних «слів» можна утворити перестановкою літер у слові «математика»? 2. У кондитерській є 6 різних сортів тістечок. Скількома способами можна купити 8 тістечок? 3. З урни, в якій 12 білих та 8 чорних кульок, виймають навмання 3 кульки. Яка ймовірність того, що всі три кульки будуть чорними. 4. Під час перевірки якості виготовлених 300 деталей було знайдено брак у 12 деталей. Знайти відносну частоту якісних деталей. 5. Відстань від міста A до міста B по автотрасі становить 100 км, а від міста B до міста C — 65 км. Вздовж автотраси проходить лінія електропередачі. Знайти ймовірність того, що під час негоди розрив лінії електропередачі відбудеться на ділянці від міста B до міста C. Рівень 3 Дайте відповіді на запитання Що називають подіями (або випадковими подіями)? Що називають вірогідною (або достовірною) подією? Що називають неможливою подією? Що називають статистичною ймовірністю? Якою формулою можна обчислити ймовірність, виходячи з геометричних міркувань? |