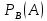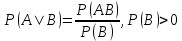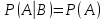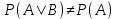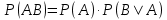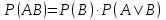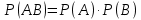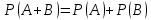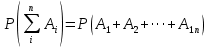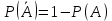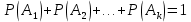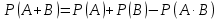практичне. ПРАКТИЧНЕ ЗАНЯТТЯ-1 (2). 1 практичне заняття 1
 Скачать 122.54 Kb. Скачать 122.54 Kb.
|
|
Приклад 9. Скількома способами два студента можуть з’їсти 10 пончиків, якщо кожен з них може з’їсти по 5? За схемою отримуємо: n=10, k=5, порядок не важливий, повторень немає. Потрібна формула: Сполучення 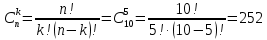 Відповідь:252 Задачі для тренування. Задача 1. Знайдіть кількість різних чотирицифрових чисел, які можна скласти з цифр 0, 3, 7, 9 (цифри в числі не повторюються). Задача 2. У деякій країні 20 міст, кожні два з яких мають авіасполучення. Скільки авіаліній у цій країні? (190) Задача 3. Студенти другого курсу згідно учбового плану вивчають 10 дисциплін. На один день можна планувати заняття з 4 дисциплін. Скількома способами можна скласти розклад занять на один день? (5040) 1.2.1. Два основні принципи комбінаторики Основне правило комбінаторики. Між скінченними множинами A та В можна встановити взаємно однозначну відповідність тоді і тільки тоді, коли вони мають однакову кількість елементів. Основне правило комбінаторики дозволяє виконувати обчислення кількості елементів множини фактично зведенням до множини з відомою кількістю елементів або до множини, для якої кількість можна підрахувати дещо простіше. У більшості випадків його використання не акцентується, а приймається як дещо зрозуміле. Значна кількість формул і теорем комбінаторики ґрунтуються на двох основних елементарних принципах, які називаються принципами суми та добутку. Принцип суми. Нехай n(A), n(B) – кількості елементів скінченних неперетинних множин А та В відповідно. Тоді для множини С = A Ս B кількість елементів обчислюється за формулою 12:
Принцип добутку. Нехай потрібно послідовно виконати k дій, причому першу дію можна виконати n1 способом, після чого другу дію – n2 способами і так далі до k-ї дії, яку можна виконати nk способами. Тоді всі k дій можна виконати 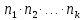 способами. способами.Розглянемо приклади обчислення класичної ймовірності за допомогою формул комбінаторики. Приклад 10. Чотирнадцять варіантів контрольної роботи написані на окремих картках і випадково розподіляються серед 12 здобувачів освіти, які сидять в одному ряду. Кожний здобувач освіти отримує одну картку. Знайти ймовірність того, що варіанти 1 і 2 не будуть використані. Розв’язання. Маємо експеримент з розподілу 14 карток серед 12 здобувачів освіти. Результатами експерименту є впорядковані (за здобувачами освіти) набори розданих 12 з 14 варіантів контрольних робіт. У цьому разі елементарні події відрізняються одна від одної не лише номерами варіантів, що розподіляються серед здобувачів освіти, а й порядком розподілу. Тому такі елементарні події є розміщеннями, а кількість усіх розміщень (елементарних подій) обчислюється за формулою: 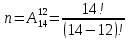 Вважаємо, що всі елементарні події рівноможливі. Нехай подія A – варіанти 1 і 2 залишаться нерозподіленими. Тоді інші 12 карток розподіляться серед 12 здобувачів освіти. Такі розподіли є перестановками, а їх кількість обчислюється за формулою: 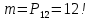 кількість елементарних подій, що сприяють події A. Отже, за формулою маємо: 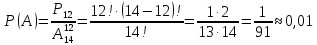 Відповідь. 0,01 Приклад 11. У групі 10 хлопців і 5 дівчат, серед яких вибирають дві особи для участі у конференції. Яка ймовірність того, що: а) Виберуть двох хлопців; б) Виберуть хлопця й дівчину? Розв’язання. У групі 15 осіб, серед яких 10 хлопців і 5 дівчат. Вибір двох осіб із 15 є сполученням, кількість яких: 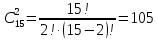 Це є загальна кількість випадків n = 15. а) Нехай подія A – вибрали двох хлопців. Кількість випадків, що сприяють події A, визначається кількістю виборів 2 хлопців із 10: 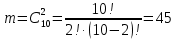 Тоді за формулою одержимо: 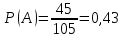 б) Нехай подія B – вибрали хлопця й дівчину. Кількість випадків, що сприяють події B, визначається кількістю виборів 1 хлопця із 10 і 1 дівчини з 5. Це можливо зробити: 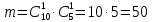 способами. Отже, 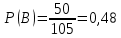 Відповідь. А) 0,43; Б) 0,48 Використання класичного означення до задач природничо-наукового або економічного характеру не завжди можливо з різних причин. Зокрема, часто неможливо подати результат експерименту як сукупність подій, які можна було б вважати рівноможливими. Наприклад, з міркувань симетрії, на яких ґрунтуються міркування про рівноймовірність подій, вивести ймовірність того, що народжена дитина була хлопчиком, неможливо. З цієї причини поряд з класичним визначенням ймовірності користуються також статистичним визначенням ймовірності, приймаючи за ймовірність події її відносну частоту. Відносна частота, поряд з ймовірністю, належить до основних понять теорії ймовірностей. Якщо позначити через μ – число появ події в n – незалежних випробуваннях, то відношення числа появ події до загального числа проведених випробувань називають відносною частотою появи даної події, тобто (формула 13)
де µ – число появ події, n – загальне число випробувань, W – відносна частота. Порівнюючи класичне визначення ймовірностей і визначення відносної частоти, можна зробити такий висновок: визначення ймовірностей не вимагає, щоб проводились випробування в дійсності; визначення відносної частоти вимагає фактичного проведення випробувань. Тобто ймовірність визначають до випробування, а відносну частоту – після випробування. Приклад 12. Відділ технічного контролю виявив у партії з 90 деталей 3 браковані деталі. Знайти відносну частоту бракованих деталей. Розв’язання. Позначимо через А таку подію, як поява бракованої деталі. Загальне число деталей n=90. Бракованих деталей є µ=3. Тоді за формулою маємо: 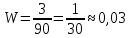 Відповідь. 0,03 Якщо дослідним шляхом встановлена відносна частота, то одержане число можна прийняти за наближене значення ймовірності. Наприклад, за даними статистики, відносна частота народження дівчат на 1000 дітей характеризується такими числами за кожен місяць (таблиця 1): Таблиця 1 – Відносна частота народження дівчат на 1000 дітей
Теореми додавання і множення ймовірностей використовують для визначення ймовірностей складних подій, які можна записати через інші події. 1.2.2 Умовна ймовірність. Залежні та незалежні події. Добуток ймовірностей. Якщо при обчисленні ймовірності події А не вказуються ніякі умови, крім комплексу умов, то такі ймовірності називаються безумовними і позначаються Р(А). Ймовірність настання події А, обчислена в припущені, що подія В уже відбулася, називається умовною ймовірністю події А при умові В і позначається (формула 14)
Словами це означає: ймовірність події А при умові, що подія В уже відбулась. Умовна ймовірність обчислюється за формулою 15:
Подію А називають незалежною від події В, якщо ймовірність події А не залежить від того, чи відбулася подія В і справедлива рівність (формула 16)
Подію А називають залежною від події В, якщо ймовірність події А залежить від того, чи відбулася подія В, тобто (формула 17)
Добутком двох подій А і В називають подію С, яка полягає в сумісному настанні цих подій. Імовірність сумісного настання двох залежних подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчисленої за умови, що перша відбулася (формули 18 та 19):
або
Для двох незалежних подій А і В (формула 20)
Приклад 13. Студент прийшов на екзамен, підготувавши лише 20 з 25 питань програми. Екзаменатор задав йому три запитання. Знайти ймовірність того, що студент знає відповіді на них. Розв’язання. Нехай подія А – студент знає відповіді на всі три запитання; подія Аі (і = 1, 2, 3) – студент знає відповідь на і-те запитання. Тоді A=A1∩A2∩A3 і за формулою умовної ймовірності: 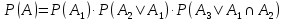 Очевидно, що 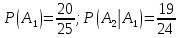 (оскільки залишилось запитань 24, з яких студент знає 19), аналогічно 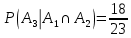 Підставивши у формулу, отримуємо: 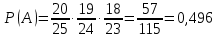 Відповідь. 0,496 1.2.3 Теорема додавання ймовірностей несумісних подій Розглянемо теореми додавання для сумісних та несумісних подій. Дві події називають несумісними, якщо вони не можуть одночасно настати в одному досліді, іншими словами, настання однієї події виключає можливість настання другої. Сумою двох подій А + В називають подію, що полягає у появі події А або події В, або обох цих подій. Наприклад, якщо зроблено два постріли А – подія, що означає влучання при першому пострілі, а В – при другому пострілі, то А+В означає влучання при першому або другому, або в обох пострілах. Зокрема, якщо дві події А і В несумісні, то А+В – подія, що полягає в появі однієї із цих подій, або події А, або події В. Сумою ∑ подій A1, A2, …, An називають таку подію, поява якої рівносильна появі принаймні однієї з подій Ai, i=1, 2, … , n. Ймовірність появи однієї з кількох несумісних подій, не важливо якої, дорівнює сумі ймовірностей цих подій (формули 21 та 22).
Ймовірність протилежної до A події 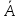 (формула 23): (формула 23):
Сума ймовірностей подій А1, А2, ..., Аk, що утворюють повну групу подій, дорівнює одиниці (формула 24):
Приклад 14. В ящику знаходиться 6 білих і 4 чорних кулі. З ящика виймають навмання 2 кулі. Яка ймовірність того, що вони однокольорові? Розв’язання. Нехай подія А – поява двох білих куль, а подія В – поява двох чорних куль. Події А та В несумісні. Число всіх єдиноможливих, рівноможливих і несумісних випадків дорівнює числу пар, які можна утворити з десяти різних куль. 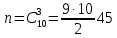 – число загальних випадків. Число випадків, сприятливих для появи двох білих куль, дорівнює 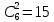 двох чорних – двох чорних – 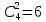 Тоді за формулою маємо: 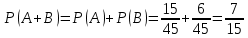 Відповідь. 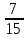 Приклад 15. У партії з 20 деталей є 16 стандартних. Знайти ймовірність того, що серед навмання взятих трьох деталей виявиться принаймні одна стандартна. Розв’язання. Нехай подія А1: виявиться одна стандартна; подія A2: виявиться дві стандартні; подія А3: виявиться три стандартні деталі. Ці події попарно несумісні. Нехай подія А: серед навмання взятих трьох деталей виявиться принаймні одна стандартна. Отже, 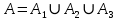 За формулою маємо: 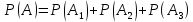 Обчислимо ймовірності подій А1, А2, А3: 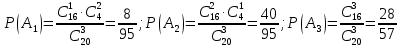 Отже, 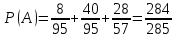 Відповідь. 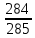 Дві події називають сумісними, якщо вони можуть одночасно настати в одному досліді, іншими словами, настання однієї події не виключає можливість настання другої. Імовірність настання принаймні однієї з двох сумісних подій А і В дорівнює сумі ймовірностей цих подій без імовірності їх спільного настання (формула 25).
|

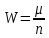
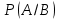 або
або