лб1. Лабораторная работа 1. 1. Правила приближенных вычислений и оценка погрешностей при вычислении
 Скачать 104.44 Kb. Скачать 104.44 Kb.
|
1. Правила приближенных вычислений и оценка погрешностей при вычисленииЦель работы: используя переменные а,b,c,d,e, данные с верными цифрами, вычислить значения функции S,U,V,W,P и их абсолютную и относительную погрешности. Результаты вычислений S,U,V,W,P округлить, оставив верные и одну сомнительную цифры. ПРИМЕР. Дано: а=13,48; b=121,51; с=3,415. Все цифры исходных данных верные. Требуется вычислить  . Результаты округлить, оставив верные и одну сомнительную цифры. . Результаты округлить, оставив верные и одну сомнительную цифры.Вычисляем абсолютные и относительные погрешности исходных данных. Абсолютную погрешность определяем исходя из того, что все цифры исходных данных верные. Относительную погрешность находим по формуле  , где , где 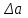 - абсолютная погрешность приближенного числа а, А - точное число. Результаты вычислений представим в виде таблицы 1.1. - абсолютная погрешность приближенного числа а, А - точное число. Результаты вычислений представим в виде таблицы 1.1.Таблица 1.1
Значение  вычисляется как сумма двух значений вычисляется как сумма двух значений 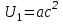 и и  . .Тогда  , а , а  . .Вычислим  и и  : : 1. |
| Значение функции | | |
| U 158,4296 158,4 | 0,11 | 0,00068 |
Отчет по самостоятельной работе должен содержать:
Таблицу исходных данных, их абсолютных и относительных погрешностей (табл. 1.3);
Заданные функции S, U, V, W, P и формулы по которым вычисляются их абсолютные и относительные погрешности;
Таблицу значений функций S S, U, V, W, P и их абсолютных и относительных погрешностей (табл. 1.4).
Таблица 1.3
| Исходные данные | | |
| a = | | |
| b = | | |
| c = | | |
| d = | | |
| e = | | |
Таблица 1.4
| Значение функции | | |
| S число до округления число после округления | | |
| U …… | | |
| V …… | | |
| W …… | | |
| P …… | | |
Теоретическая часть
Определение. Абсолютной погрешностью
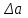 приближенного числа а называют абсолютную величину разности между точным числом А и его приближенным значением а:
приближенного числа а называют абсолютную величину разности между точным числом А и его приближенным значением а: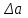 =|А-а|.
=|А-а|.Если точное число А не известно, тогда вводится понятие предельной абсолютной погрешности
 , т.е. границы (оценки) абсолютной погрешности
, т.е. границы (оценки) абсолютной погрешности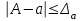 .
.Определение. Относительной погрешностью
 приближенного числа а называют отношение абсолютной погрешности
приближенного числа а называют отношение абсолютной погрешности 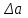 к модулю точного числа А (А0):
к модулю точного числа А (А0): .
.Замечание. На практике
 , поэтому
, поэтому  .
.Определение. Предельная относительная погрешность
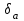 , т.е. границы (оценки) относительной погрешности, имеет вид:
, т.е. границы (оценки) относительной погрешности, имеет вид: , причем
, причем  .
.Оценка погрешностей при вычислении
Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел.
Пусть
 . Тогда
. Тогда 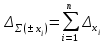 ,
,т.е. при сложении и вычитании приближенных чисел их предельные абсолютные погрешности складываются.
Относительная погрешность суммы n положительных приближенных чисел не превосходит максимальной относительной погрешности слагаемых.
Пусть
 , причем границы относительных погрешностей приближенных чисел
, причем границы относительных погрешностей приближенных чисел  равны
равны  соответственно.
соответственно.Тогда

 , где
, где  .
.Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел.
Пусть
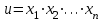 , где можно считать все сомножители положительными. Тогда
, где можно считать все сомножители положительными. Тогда  .
.При умножении и делении приближенных чисел их предельные относительные погрешности складываются.
Пусть
 , где
, где  ,
, >0, тогда
>0, тогда  .
.При умножении приближенного числа х на точный множитель k предельная относительная погрешность не изменяется, а предельная абсолютная погрешность увеличивается в
 раз:
раз:  ,
, 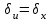
 .
.Предельная относительная погрешность m-й степени числа в m раз больше предельной относительной погрешности самого числа
 ,
,  .
.Варианты лабораторных работ
| Вариант | а | b | c | d | e | Вариант |
| 1 | 3,418 | 7,241 | 18,315 | 32,01 | 0,4721 | 1 |
| 2 | 2,4154 | 1,3127 | 41,15 | 5,180 | 21,135 | 2 |
| 3 | 15,487 | 10,401 | 12,318 | 1,4158 | 7,0013 | 3 |
| 4 | 2,4172 | 1,3120 | 9,1318 | 18,145 | 21,418 | 4 |
| 5 | 17,425 | 10,815 | 11,211 | 2,4150 | 7,1327 | 5 |
| 6 | 7,4138 | 1,1310 | 9,1315 | 17,415 | 25,135 | 6 |
| 7 | 17,48 | 10,120 | 41,01 | 1,349 | 8,4251 | 7 |
| 8 | 2,817 | 9,3156 | 4,442 | 17,480 | 13,55 | 8 |
| 9 | 13,85 | 25,140 | 31,15 | 7,8153 | 9,314 | 9 |
| 10 | 7,3148 | 1,4145 | 6,317 | 17,18 | 21,10 | 10 |
| 11 | 21,18 | 35,48 | 10,10 | 1,418 | 5,4012 | 11 |
| 12 | 17,485 | 10,817 | 2,4831 | 25,40 | 3,25 | 12 |
| 13 | 3,40 | 7,823 | 9,312 | 0,9192 | 17,42 | 13 |
| 14 | 13,481 | 15,40 | 27,31 | 2,3155 | 1,2001 | 14 |
| 15 | 7,0809 | 3,2540 | 9,35 | 17,011 | 25,148 | 15 |
| 16 | 3,0714 | 7,4142 | 1,32 | 14,810 | 21,799 | 16 |
| 17 | 14,418 | 10,875 | 13,301 | 1,41 | 9,1310 | 17 |
| 18 | 3,7118 | 9,340 | 8,75 | 17,455 | 25,785 | 18 |
| 19 | 0,4152 | 1,34 | 7,2530 | 12,485 | 25,327 | 19 |
| 20 | 7,42 | 3,2521 | 2,0045 | 21,348 | 14,500 | 20 |
| 21 | 3,4180 | 2,3754 | 9,00 | 18,015 | 21,524 | 21 |
| 22 | 17,418 | 21,310 | 35,001 | 7,35 | 3,4849 | 22 |
| 23 | 9,1240 | 1,3504 | 2,3104 | 13,275 | 21,32 | 23 |
| 24 | 18,348 | 27,218 | 40,10 | 4,1841 | 9,1945 | 24 |
| 25 | 7,415 | 1,3495 | 8,1920 | 17,485 | 25,371 | 25 |
| 26 | 12,237 | 27,790 | 30,14 | 7,1318 | 9,9571 | 26 |
| 27 | 17,835 | 21,113 | 11,004 | 3,140 | 1,0204 | 27 |
| 28 | 5,142 | 4,3560 | 12,27 | 7,1213 | 0,9991 | 28 |
| 29 | 2,5472 | 0,248 | 24,513 | 1,12 | 16,2510 | 29 |
| 30 | 0,2456 | 7,4182 | 3,651 | 13,84 | 12,50 | 30 |
| Вариант | S | U | V | W | P | Вариант |
| 1 | 2a-3b+4c | ade | b/d | (a3b2c2e)/d2 | a3b+dc+e | 1 |
| 2 | 3a+5b-2d | abe | a/d | (a2b3d2c)/e2 | ab3+bc+ed | 2 |
| 3 | 4a+5b-2c | ace | b/e | (ab2d3)/ 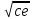 | ad-e2+bc | 3 |
| 4 | 2a+10b-c | bce | c/e | (b4c2e)/(a3d) | a2d+b3e-c | 4 |
| 5 | 2c-a+7b | abd | c/d | (ab2e2)/(cd3) | ad2-b+ce | 5 |
| 6 | 4c-5b+8a | abe | d/c | (a3b2c2)/(de) | ad+b3e+c | 6 |
| 7 | 2c+5b-2a | ade | c/e | (ab2e2)/(dc) | ae+d2c+b | 7 |
| 8 | 5b+4c-2a | ace | d/a | (a3b2d)/(c3e) | ad+be+c2 | 8 |
| 9 | 5b-2c+a | ade | a/e | (a2d2b)/(ce3) | ad2+bc+e | 9 |
| 10 | 10b+3c-2a | ace | e/a | (ab3e)/(c3d) | b3e+a2+cd | 10 |
| 11 | 2b+2a+5c | ade | b/e | (abd3)/(ce) | bd2+ac-e | 11 |
| 12 | 2a-d+3b | ace | d/b | (  bc2)/(de2) bc2)/(de2) | ac2-e2+bd | 12 |
| 13 | 10a-c+4b | ade | c/a | (a2ec)/(b2d3) | ac+e-b2d | 13 |
| 14 | 5a+b-2c | adb | b/d | (ad2b)/(e3c) | ab+d2c-e4 | 14 |
| 15 | 3a+b-2c | ace | d/c | (a2b3d)/(ce) | ac-d2+bc | 15 |
| 16 | 10a-5c+3b | acd | d/b | (a2c2e)/(b2d) | c2e+bd-a2 | 16 |
| 17 | 5a-b+3c | ace | b/e | (ad3e2)/(bc) | ae+b2+cd | 17 |
| 18 | 10a+5b-c | bcd | d/b | (a2be)/(c2d) | a2c+bd+e | 18 |
| 19 | 7a+8b-c | acd | d/c | (ab2e)/(c2d) | ac2-bd+e | 19 |
| 20 | 2c+7b-a | acd | d/a | (b2c3e)/(a2d) | a2c+be-d | 20 |
| 21 | 7a+4c-3b | ade | e/c | (a3ce)/(b2d) | a2d+e+b2c | 21 |
| 22 | 2a+3b-c | abd | c/a | (ace2)/(d3b) | ae3+d2+bc | 22 |
| 23 | 3b+9c-a | ade | e/a | (ab2d)/(c2e) | ad+b2e+c3 | 23 |
| 24 | 2a+4b-c | abc | b/c | (acd2)/(be2) | ae+d2+bc | 24 |
| 25 | 5a+10b-c | ace | e/c | (a2ec)/(b3d) | a2c+b3e-d | 25 |
| 26 | 6a+2b+c | abc | c/b | (a2e)/(bcd2) | ad2+be-c | 26 |
| 27 | 3c-2b+c | dec | b/c | (e3ac)/(b2  ) ) | d2a+be3+c | 27 |
| 28 | 6a-5b-d | acd | a/b | (ab3c)/(d2e) | ab+c2d-e3 | 28 |
| 29 | 4a+5b+d | bcd | b/d | (a2b 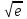 )/(c3d) )/(c3d) | a2d-b2c+e | 29 |
| 30 | 3a-2b+c | ade | d/e | (ab2c3)/(de) | ab2-dc+e | 30 |

 157,2067;
157,2067;  0,00068;
0,00068;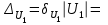 0,1069.
0,1069. 1,2229;
1,2229; 0,00041;
0,00041;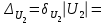 0,0005.
0,0005. 158,4296;
158,4296; 0,1074
0,1074 0,11;
0,11;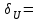 0,00068.
0,00068. 0,11<0,5, то значение U содержит три верные значащие цифры (1, 5, 8), остальные цифры являются сомнительными. Округлим значение U, оставив только верные и одну сомнительную цифры. Данные представим в виде таблицы 1.2.
0,11<0,5, то значение U содержит три верные значащие цифры (1, 5, 8), остальные цифры являются сомнительными. Округлим значение U, оставив только верные и одну сомнительную цифры. Данные представим в виде таблицы 1.2.