1. Предмет Геодезия и ее задачи

• Название: 1. Предмет Геодезия и ее задачи
• Дата: 17.05.2022
• Размер: 128.1 Kb.
• Имя файла: Geodezi111.docx
• Тип: Документы; #535297
• страница: 2 из 6

3. Классификация геодезических сетей. С точки зрения геометрии любая геодезическая сеть - это группа зафиксированных на местности точек, для которых определены плановые координаты - (X), (Y) и отметки (H) в принятой системе высот.

Все геодезические сети по назначению и точности построения подразделяются на три большие группы: 1) государственные геодезические сети (ГГС): 2) геодезические сети сгущения (ГСС); 3) геодезические съемочные сети.

Государственная геодезическая сеть (ГГС) является главной геодезической основой топографических съемок всех масштабов и должна удовлетворять требованиям народного хозяйства и обороны страны при решении соответствующих научных и инженерно-технических задач.

Плановая сеть создается методами триангуляции, полигонометрии, трилатерации и их сочетаниями; высотная сеть создается построением нивелирных ходов и сетей геометрического нивелирования.

Триангуляция – это метод построения плановой геодезической сети в виде примыкающих к друг другу треугольников, в которых измеряют все углы и длину хотя бы одной стороны, называемой базисом или базисной стороной.

Трилатерация – это метод построения плановой геодезической сети в виде примыкающих к друг другу треугольников, в которых измеряют длины всех сторон. Группа треугольников, как и в триангуляции, образует либо сплошную сеть, либо цепочку треугольников.

Полигонометрия – это метод построения геодезической сети в виде замкнутых или разомкнутых ломанных линий, в которых непосредственно измеряются все элементы: углы поворота и и длины сторон.

Государственная геодезическая сеть подразделяется на сети 1,2, 3 и 4 классов, различающиеся точностью измерений углов, расстояний и превышений, длиной сторон сети и порядком последовательного развития.

№ 7. 1. Cведения о фигуре Земли. _Предметом геодезии является планета Земля. Общая площадь Земли – 510 млн. км2; 71% поверхности Земли – это моря и океаны, 29% – суша. При определении положения точек земной поверхности обычно относят их к общей фигуре Земли, которую называют геоидом. Геоид – это геометрическое тело, ограниченное уровенной поверхностью. _Уровенная поверхность – поверхность, совпадающая с поверхностью воды в морях и океанах, которые находятся в спокойном состоянии, продолженная под материками. На местности точки, линии, углы и контуры расположены в силу неровностей земной поверхности на возвышениях или впадинах. Так как возвышения и впадины являются пространственными формами, изобразить их на бумаге в виде плоской карты или плана достаточно непросто. Способы изображения земной поверхности на плоскости основываются на методе проекций.

_______При изучении действительной поверхности Земли точки местности проецируют отвесными линиями на поверхность земного эллипсоида. Так как уровенная поверхность радиусом до 20 км может быть заменена плоскостью, при относительно небольших площадях, точки местности проецируют на горизонтальную плоскость. Положение полученных проекций точек может быть определено координатами.

_______В результате перенесения точек на плоскость длины линий заменяют их горизонтальными проекциями, называемыми горизонтальными проложениями; пространственные углы заменяются плоскими, и вся фигура заменяется проекцией на горизонтальную плоскость. _Широта отсчитывается по дуге меридиана к северу и к югу от экватора от 0° до 90°. К северу от экватора широта называется северной, к югу – южной.

_______Долгота отсчитывается от меридиана, проходящего через Гринвич на окраине Лондона. Долгота отсчитывается по дуге экватора или параллели от начального меридиана в сторону востока и запада от 0° до 180°. Долгота к востоку от Гринвичского меридиана называется восточной долготой, к западу – западной. Широты и долготы определяют положение любой точки на земной поверхности и выражаются в угловой мере. Географические координаты определяются из астрономических наблюдений и, а также с помощью геодезических измерений.
2. Румбы линий. Кроме географического и магнитного азимутов и дирекционного угла к ориентирным углам относятся также румбы. Румб - это острый угол от ближайшего направления меридиана до направления линии; он обозначается буквой (r). Пределы изменения румба от 0^o до 90^o. Название румба зависит от названия меридиана: географический, магнитный и дирекционный (или осевой). Для однозначного определения направления по значению румба он сопровождается названием четверти: І четверть - СВ (северо-восток), ІІ четверть - ЮВ (юго-восток), ІІІ четверть - ЮЗ (юго-запад), ІV четверть - СЗ (северо-запад), например, r = 30^o ЮВ.

Связь румба с соответствующим азимутом или дирекционным углом выявляется из рисунка 12.2 «Положение румба по четвертям»..І четверть: A(α) = r , ІІ четверть: A(α) = 180^° - r..ІІІ четверть: A(α) = r - 180^° , ІV четверть: A(α) =360^° - r (14.4)

3.Закрепление геодезических пунктов на местности. Закрепленная на местности точка геодезической сети называется геодезическим пунктом. На местности геодезические пункты отмечаются центрами и опознавательными знаками. Типы центров и опознавательных знаков бывают самые разноообразные; они зависят от типа и точности геодезической сети, от климатических, почвенных и других характеристик местности. Геодезические пункты должны быть достаточно прочными и долговечными, чтобы сохранить неизменное положение центра в течение длительного времени, и находиться в удобном месте, обеспечивающем быстрое его обнаружение и опознавание.
№ 8. 1.Эллипсоид вращения, эллипсоид Крассовского.

Эллипсо́ид Красо́вского — референц-эллипсоид земной поверхности, форма и размеры которого были вычислены советским геодезистом А. А. Изотовым и который в 1940 году назван именем Ф. Н. Красовского^[1]. Центр референц-эллипсоида Красовского совпадает с началом референцной системы координат, ось вращения эллипсоида параллельна оси вращения Земли, а плоскость нулевого меридиана определяет положение начала отсчёта долгот^[2]. Одно из вторых приближений фигуры Земли (первое приближение — шар).

Эллипсоид Красовского характеризуется следующими величинами: – большая полуось a 6378 245 м; – сжатие Земли 1: 298,3. Положение (ориентировка) эллипсоида Красовского в теле Земли определено геодезическими координатами центра круглого зала Пулковской обсерватории: широта B0 = 59°46'18,55", долгота L0 = 30°19'42,09", высота x0 положена равной нулю. Эти исходные геодезические даты, как и эллипсоид Красовского, приняты за основу единой государственной системы координат СК-95 при производстве всех геодезических и картографических работ на территории РФ. До 1946 года в России применялся земной эллипсоид Бесселя, размеры которого оказались ошибочными. Эллипсоид Красовского применяется также в геодезических и картографических работах всех стран бывшего СССР, в странах восточной Европы, Китае, Индии, КНДР, Южной Корее, Монголии и в других странах.  
2. Прямая геодезическая задача на плоскости. В геодезии есть две стандартные задачи: прямая геодезичеcкая задача на плоскости и обратная геодезическая задача на плоскости. Прямая геодезическая задача - это вычисление координат (X₂), (Y₂) второго пункта, если известны координаты (X₁), (Y₁) первого пункта, дирекционный угол (α) и длина (S) линии, соединяющей эти пункты.

Спроектируем точки (1) и (2) на оси координат (рисунок 11). Проекция линии (S) на ось (Х), очевидно будет равна отрезку, называемому приращением координат по оси абсцисс (∆х), а на ось (У) – приращению координат по оси ординат (∆y).. ∆х = х₂ – х₁….∆y = y₂ – y₁

В зависимости от величины дирекционного угла приращения координат могут иметь различные знаки. Знаки приращений определяются знаками тригонометрических функций (sin) и (cos) соответствующей четверти.

3.Съемочное обоснование топографических съемок.

Комплекс работ, в результате выполнения которого получают карту или план местности, называют топографической съемкой.

Принцип съемки заключается в том, что на местности создается сеть опорных точек, взаимное положение которых в принятой системе координат определяют в первую очередь. Затем прибор для съемки устанавливают последовательно на каждую опорную точку и снимают ситуацию и рельеф в промежутках между ними, определяя положение точек местности относительно опорных точек и соединяющих их линий.

Точки, на которые устанавливают прибор для съемки, закрепляют на местности; их называют пунктами съемочного обоснования. Их координаты и отметки определяют из геодезических измерений, как правило, до начала съемки. По Инструкции средняя ошибка планового положения пунктов съемочного обоснования допускается 0.1 мм в масштабе плана. Этот допуск определяется точностью графических построений.
№ 9.1.Геодезические координаты. Положение точки на поверхности сферы определяется двумя сферическими координатами - широтой (φ) и долготой (λ). Широту и долготу точек местности определяют из астрономических наблюдений, потому они и называются астрономическими координатами.

На поверхности эллипсоида вращения положение точки определяется геодезическими координатами - геодезической широтой (B) и геодезической долготой (L)

Геодезическая долгота точки - это двугранный угол между плоскостью начального меридиана и плоскостью меридиана точки.

Геодезическая широта точки - это угол, образованный нормалью к поверхности эллипсоида в этой точке и плоскостью экватора.

Плоскость геодезического меридиана проходит через точку (A) и малую полуось эллипсоида; в этой плоскости лежит нормаль к поверхности эллипсоида в точке (A). Геодезическая параллель получается от пересечения поверхности эллипсоида плоскостью, проходящей через точку (A) и параллельной плоскости экватора.

При геодезических работах невысокой точности астрономические и геодезические координаты не различают; их общее название - географические координаты - используется довольно часто.

2.Обратная геодезическая задача на плоскости. Обратная геодезическая задача - это вычисление дирекционного угла (α) и длины (S) линии, соединяющей два пункта с известными координатами (X₁), (Y₁) и (X₂), (Y₂). Рассмотрим прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна (S), катеты равны приращениям координат точек (1) и (2), вычисленным по формулам (8), а один из острых углов равен румбу (r) линии (1-2). Если Δ X 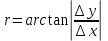0 и Δ Y 0, то решаем треугольник по известным формулам: ,,,   ,  

Для данного рисунка направление линии (1-2) находится во второй четверти, поэтому находим:α = 180^° - r

Общий порядок нахождения дирекционного угла линии (1-2) включает две операции: 1) определение номера четверти по знакам приращений координат (Δх) и (Δу); 2) вычисление (α) по формулам связи (10) в соответствии с номером четверти.

Контролем правильности вычислений является выполнение равенства: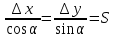        

3.Принцип топографической съемки. Съемка подробностей. Съемка местности сводится к определению координат и отметок отдельных точек, характеризующих местоположение объектов местности и ее рельеф.

Средняя ошибка положения точечного объекта или четкого контура на плане относительно ближайших пунктов съемочного обоснования допускается 0.5 мм (в горной и лесной местности - 0.7 мм). Эта величина называется точностью плана. Ошибка изображения рельефа зависит от характера рельефа и обычно равна одной трети высоты сечения рельефа.

3. Общие сведения о съемках местности. Если съемка производится для получения плана с изображением ситуации, то ее называют горизонтальной или плановой.

Съемка, в результате которой должен быть получен план или карта с изображением ситуации и рельефа, называется топографической. При топографической съемке наряду с другими действиями производят измерения с целью определения высот точек местности, т. е. нивелирование. В зависимости от применяемых приборов и методов различают следующие виды съемок.

Теодолитная съемка — это горизонтальная съемка местности, выполняемая с помощью угломерного прибора — теодолита и стальной мерной ленты (или оптического дальномера). При выполнении этой съемки измеряются горизонтальные углы и расстояния. В результате съемки получают ситуационный план местности с изображением контуров и местных предметов.

Тахеометрическая съемка В отличие от теодолитной, тахеометрическая съемка, кроме ситуации, позволяет одновременно получать данные для вычерчивания рельефа местности. При этом на местности измеряют горизонтальные и вертикальные углы и расстояния до точек. По результатам измерений в камеральных условиях строится топографический план местности.

Мензульная съемка производится при помощи мензулы — горизонтального столика и кипрегеля — специального углоначертательного прибора, снабженного вертикальным кругом и дальномером. В процессе этой съемки топографический план местности составляется непосредственно в поле, что позволяет сопоставлять полученный план с изображаемой местностью. В этом заключается достоинство мензульной съемки по сравнению с тахеометрической.

Наземная фототопографическая съемка выполняется фототеодолитом, представляющим собой сочетание теодолита и фотокамеры. Путем фотографирования местности с двух точек линии (базиса) и последующей обработки фотоснимков на специальных фотограмметрических приборах получают топографический план снимаемого участка местности. Данная съемка применяется при дорожных, геологических и других изысканиях в горной местности и в маркшейдерском деле при съемках карьеров.

Воздушная фототопографическая съемка производится специальными аэрофотоаппаратами, устанавливаемыми на самолетах. Для обеспечения этой съемки на местности выполняются определенные геодезические измерения, необходимые для планово-высотной привязки аэроснимков к опорным точкам местности. Данный вид съемок позволяет в кратчайшие сроки получить топографические планы (карты) значительных территорий страны.

Нивелирование ( вертикальная или высотная съемка) производится с целью определения высот точек земной поверхности.

Глазомерная съемка - контурная съемка местности, выполняемая на планшете с компасом при помощи визирной линейки. В инженерной практике данная съемка применяется при предварительном ознакомлении с местностью, а также при изысканиях в неисследованных районах.
№ 10.1.Плоские прямоугольные координаты. Систему плоских прямоугольных координат образуют две взаимно перпендикулярные прямые линии, называемые осями координат; точка их пересечения называется началом или нулем системы координат. Ось абсцисс – (OX), ось ординат – (OY)

Положение точки в прямоугольной системе однозначно определяется двумя координатами (X) и (Y). Значения координат бывают положительные (со знаком «+») и отрицательные (со знаком «-») в зависимости от того, в какой четверти (квадранте) находится искомая точка. 2.Принцип измерения горизонтального угла. Плоский угол образуется двумя лучами, исходящими из одной точки, называемой вершиной угла. Угол обычно измеряют в градусной мере (градусы, минуты, секунды), реже - в радианной; за рубежом широко применяется градовая мера измерения углов. В геодезии имеют дело с углами, лежащими в горизонтальной или вертикальной плоскостях, причем горизонтальный угол обычно обозначают буквой (β, а вертикальный (ν).

На местности угол фиксируется тремя точками: одна из них - точка (A) - является вершиной угла, две другие – (B) и (C) - фиксируют направления

Таким образом, прибор для измерения горизонтальных углов на местности должен иметь угломерный круг, приспособление для наведения на точки местности и устройство для отсчитывании по шкале угломерного круга; такой прибор называется теодолитом.

3. Общие сведения о съемках местности Если съемка производится для получения плана с изображением ситуации, то ее называют горизонтальной или плановой.Съемка, в результате которой должен быть получен план или карта с изображением ситуации и рельефа, называется топографической. При топографической съемке наряду с другими действиями производят измерения с целью определения высот точек местности, т. е. нивелирование. В зависимости от применяемых приборов и методов различают следующие виды съемок.Теодолитная съемка — это горизонтальная съемка местности, выполняемая с помощью угломерного прибора — теодолита и стальной мерной ленты (или оптического дальномера). При выполнении этой съемки измеряются горизонтальные углы и расстояния. В результате съемки получают ситуационный план местности с изображением контуров и местных предметов.
№ 11..1.Система высот. Для определения положения точки в трехмерном пространстве нужно задать ее третью координату, которой в геодезии является высота.Высотой точки называется расстояние по отвесному направлению от этой точки до уровенной поверхности. Числовое значение высоты точки называется ее отметкой. Высоты бывают абсолютные, условные и относительные (рисунок 4 – «Абсолютные, условные и относительные высоты»).

Абсолютные высоты, например Н_А и Н_В, отсчитывают от исходной уровенной поверхности – среднего уровня океана или моря. В нашей стране счет высот ведется от уровенной поверхности, соответствующей среднему уровню Балтийского моря (от нуля Кронштадтского футштока); эта система высот называется Балтийской.

Условной высотой, например Н_{В усл}, называется отвесное расстояние от точки земной поверхности до условной уровенной поверхности – любой точки, принятой за исходную (нулевую).

Относительной высотой, или превышением (h) точки, называется высота ее над другой точкой земной поверхности (например, точки (В) над точкой (А)).h_AB = H_B - H_A