расчетно-графическая работа геодезия. РГР №1 — копия. Обработка материалов геодезистких измерений, выполненных при создании планового съемочного обоснования
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
|
ОБРАБОТКА МАТЕРИАЛОВ ГЕОДЕЗИСТКИХ ИЗМЕРЕНИЙ, ВЫПОЛНЕННЫХ ПРИ СОЗДАНИИ ПЛАНОВОГО СЪЕМОЧНОГО ОБОСНОВАНИЯ Геодезическое съемочное обоснование – это система закрепленных на местности точек, координаты которых известны. С точек съемочного обоснования производится съемка местности. Плановое съемочное обоснование для различных видов топографической съемки обычно создают прокладкой теодолитных ходов. При прокладке теодолитных ходов в поле измеряют длины линий между точками с точностью 1:2000 и углы между сторонами хода с точностью 30''. Для вычисления координат точек в принятой на объекте системе координат выполняют геодезическую привязку хода к пунктам геодезических опорных сетей, т.е. определяют координаты начальной точки и дирекционный угол начальной стороны хода. После окончания полевых измерений производят их камеральную обработку. В результате выполнения работы студенты должны научиться вычислять координаты точек теодолитных ходов и усвоить методику обработки геодезических измерений. Вычисления выполняют с помощью микрокалькуляторов или ЭВМ, используя электронную таблицу Excel. Исходные данные для выполнения работы При создании планового съемочного обоснования был проложен замкнутый теодолитный ход из четырех точек. Исходными данными для выполнения работы являются: внутренние (правые по ходу) горизонтальные углы β на точках хода, горизонтальные проложения d сторон, координаты х1 , у1 первой (начальной) точки хода и дирекционный угол α1-2 первой (начальной) стороны хода (приложение 1). Значения горизонтальных углов и горизонтальных проложений являются общими для всех студентов. Дирекционный угол первой стороны хода, определяемые из геодезической привязки, выдается каждому студенту индивидуально (приложение 1). Схема хода показана на рис.1.  Рис. 1. Схема теодолитного хода Уравнивание горизонтальных углов хода Уравнивание – это процесс обработки результатов измерений, при котором: 1) производят контроль и оценку качества выполненных измерений; 2) находят наиболее вероятные значения измеренных величин (углов, линий) и их функций (дирекционных углов линий, координат точек). Решение первой части задачи уравнивания состоит в определении невязок и оценке их допустимости. Решение второй части состоит: - в распределении невязок, т.е. в нахождении по определенным правилам поправок к измеренным и вычисленным величинам; - в вычислении уравненных значений искомых величин. В замкнутом теодолитном ходе три избыточных измерения (два угла и одна линия), которые приводят к возникновению трех геометрических условий. Эти условия можно записать в виде трех условных уравнений: 1) ∑βи - ∑βт= fβ ; 2) ∑Δхвыч = ƒx ; 3) ∑Δувыч = ƒу . Индексы в уравнениях означают измеренные, теоретические и вычисленные величины. В правых частях уравнений стоят невязки, являющиеся результатом накопления погрешностей измерения углов и линий. Студенты выполняют уравнивание теодолитного хода в специальной ведомости (табл. 1), в которую уже вписаны все необходимые данные. Таблица 1 Вычисление координат точек съёмочного обоснования
∑ 359º 59,0' 360º 00' 659 + 0,23 - 0,06 0 0 180º(п-2)= 360º 00' ƒр=  = 0,24 = 0,24 ƒβ= - 1,0'____  = =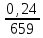 = =  ; ;  < < доп.ƒβ 1′ 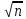 = ± 2' = ± 2' / fβ/ ≤ / доп. /fβ/ 1.2.1. Уравнивание горизонтальных углов Уравнивание горизонтальных углов выполняются в графах 2,3 ведомости в следующем порядке: 1. Вычисляют сумму измеренных углов ∑βи, результат записывают в суммарную графу 2. 2. Вычисляют теоретическое значение ∑βт суммы углов хода по формуле ∑βтеор =180о (n-2), где n – число точек хода. 3. Вычисляют угловую невязку хода fβ = ∑βи - ∑βт. 4. Вычисляют допустимое значение угловой невязки по формуле: доп.fβ = 1′ 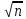 . .5. Сравнивают полученную невязку с допустимой. Если / fβ / ≤ / доп. fβ/, то невязку fβ распределяют с обратным знаком примерно поровну по всем измеренным углам, т.е. вычисляют правки δβокругляя их до 0,5′. Эти поправки выписывают над измеренными углами. Контроль вычисления правок: ∑ δβ = - fβ. 6. В графе 3 вычисляют уравненные значения углов и их сумму. Эта сумма уравненных углов должна точно равняться ∑βт. 1.2.2. Вычисление дирекционных углов сторон хода Дирекционные углы сторон хода вычисляют в графе 4 по заданному дирекционному углу стороны 1-2 и уравненным значениям горизонтальных (правых) углов по формуле αк+1 = αк + 180о – βП, где αк+1 – дирекционный угол последующей стороны хода, αк – дирекционный угол предыдущей стороны, βП – правый горизонтальный угол между этими сторонами. Если при вычислении величина дирекционного угла окажется больше 360о, то из результата следует вычесть 360о. Контроль вычислений: использовав все углы замкнутого хода из графы 3, снова получают значение дирекционного угла стороны 1-2. Пример вычисления дирекционных углов: α2-3 = α1-2 + 180о –β2 = 125о30’ + 180о – 97о58’ = 207о32’ , α3-4 = α2-3 + 180о –β3 = 207o32’ + 180o – 91o25’ = 296o07’ , α4-1 = α3-4 + 180о –β4 = 296o07’ + 180o – 77o31’ = 38o36’ , α1-2 = α4-1 +180o – β1 = 38o36’ +180o – 93o06’ = 125o30’ (контроль). 1.2.3. Вычисление и уравнивание приращений координат Эти вычисления выполняют в графах 6–9 ведомости. Приращения координат вычисляются с помощью микрокалькулятора по формулам: Δх = d  cosα, Δу = d cosα, Δу = d  sinα, sinα,где d – горизонтальное положение стороны хода, α – дирекционный угол той же стороны. При вычислениях следует помнить, что дирекционные углы вычислены в градусах и минутах, а калькуляторы воспринимают углы в десятичных долях градуса. Поэтому перед вычислением приращений минуты дирекционных углов нужно преобразовать в десятичные доли градуса, используя специальную клавишу преобразования DMS → или ° ′ ″→. При вычислении приращений удобно пользоваться специальными клавишами aи b на однострочных или Pol( на двустрочных калькуляторах, которые предназначены для решения прямой геодезической задачи. Сначала вводят длину линии, затем дирекционный угол. Примеры вычисления приращений координат на разных калькуляторах: КалькуляторCitizen SR-135 204.42 a 30.12 DMS b SHIFT b (Δx) 176.68 b (Δy) 102.83 226.09 a 110.35 DMS b SHIFT b (Δx) -79.49 b (Δy) 211.67 КалькуляторSTF-169 204.42 ALFA 0 30.12 DMS SHIFT . (Δx) 176.68 ►(Δy) 102.83 226.09 ALFA 0 110.35 DMS SHIFT . (Δx) -79.68 ►(Δy) 211.67 КалькуляторCitizen SR-281 2nd P→R 204.42 2nd , 30 ° ′ ″ 12° ′ ″ = 176.68 2nd x↔y (Δy) 102.83 Калькулятор Citizen fx-82MS SHIT Pol(204.42 , 30 ° ′ ″ 12° ′ ″) = 176,68 RCL tan 102.83 SHIT Pol(226.09 , 110 ° ′ ″ 35° ′ ″) = -79,49 RCL tan 211,67 Вычислительные значения приращений округляют до 0,01 м и со своими знаками вписывают в графы 6, 7. В суммарной строке этих же граф находят координатные невязки ƒx и ƒу : ƒx = ∑Δх, ƒy = ∑Δу . В суммарной строке графы 5 записывают значение периметра хода Р с точностью до метра. Для оценки допустимости координатных невязок ƒx и ƒy вычисляют абсолютную невязку в периметре хода ƒр =  и относительную невязку и относительную невязку 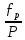 . .Относительную невязку выражают дробью с числителем, равным 1. В знаменателе следует сохранить две значащие цифры, например, 2600. Сравнивают полученную относительную невязку с допустимой. В задании допустимую относительную невязку хода принимают равной 1/2000. Если относительная невязка недопустима, т.е. если знаменатель невязки меньше 2000, то проверяют правильность вычисления дирекционных углов и приращений координат, правильность их суммирования. Если относительная невязка допустима, то допустимы и координатные невязки ƒx и ƒy. Их распределяют с обратным знаком по всем приращениям прямо пропорционально длинам горизонтальным положениям сторон хода (графа 5), т.е. вычисляют правки δхi , δуi по формулам: δхi = -  di ,δуi = - di ,δуi = -  di diПоправки δхi , δуi в сантиметрах выписывают над приращениями координат в графах 6, 7. Контроль вычисления поправок: ∑ δхi =-ƒx , ∑ δуi = -ƒy . Если этот контроль не выполняется на 1-2 см, то вычисленные поправки δхi и δуi следует округлить так, чтобы суммы поправок точно равнялись невязкам с обратным знаком. В графах 8, 9 вычисляют уравненные значения Δxi′ и Δyi′ приращений координат, учитывая и знак приращения, и знак поправки: Δxi′= Δхi + δхi , Δyi′= Δyi + δyi Контроль вычислений: суммы уравненных приращений должны точно равняться нулю ∑Δх = 0, ∑Δу = 0. Если этот контроль не получается, то следует проверить правильность вычисления невязок ƒx и ƒy, знаки поправок δх и δу, учет этих знаков при вычислении уравненных приращений. 1.2.4. Вычисление координат точек хода По заданным координатам точки 1 и уравненным приращениям координат вычисляют координаты всех точек хода: хk+1 = хk+ Δxi′ , уk+1 = уk + Δyi′ . Контроль вычислений: использовав все приращения координат из граф 8, 9, получают снова заданные координаты первой точки. На этом вычисления заканчиваются. Ведомость аккуратно оформляют в соответствии с табл. 1 и образцами, вывешенными в лабораториях кафедры. Эта ведомость является отчетным документом по выполненной работе. СОСТАВЛЕНИЕ ПЛАНА ГОРИЗОНТАЛЬНОЙ СЪЕМКИ В МАСШТАБЕ 1:2000 Горизонтальную (теодолитную) съемку выполняют для получения контурного (ситуационного) плана участка местности, например, для получения масштабного плана железнодорожной станции. Материалами съемки являются журналы измерений и абрисы – схематические чертежи с указанными на них промерами. В результате выполнения работы студенты должны научиться составлять и вычерчивать контурный план участка местности. Порядок выполнения работы: - построение координатной сетки; - нанесение на план точек съемочного обоснования с контролем; - нанесение контурных точек и составление контурного плана; - оформление и вычерчивание плана. Эту работу студенты могут выполнять вручную или с использованием любого графического редактора: Компас, Автокад и т.п. 2.1. Исходные данные для выполнения работы Исходными данными для выполнения работы служат найденные в предыдущей работе координаты точек теодолитного хода, абрис и журнал съемки с точки 3. Съемка производилась способами: перпендикуляров, полярных координат, пересечения створов, обмером сооружений 2.2. Построение координатной сетки На планах всех масштабов координатные линии проводят через 10 сантиметров. Это соответствует 200 м на плане масштаба 1:2000. Точность графических построений 0,1- 0,2 мм. Для получения такой точности координатную сетку строят с помощью циркуля-измерителя и точной линейки (например, масштабной линейки). От точности построения координатной сетки зависит правильность выполнения всей работы, поэтому сетку нужно строить очень тщательно. Следует помнить, что ось Х на плане должна быть направленна вертикально. На листе чертежной бумаги формата А4 твердым, остро отточенным карандашом проводят диагонали, точку их пересечения накалывают. От этой точки измерителем откладывают на полудиагоналях равные отрезки длиной около 13 см. Концы отрезков накалывают (точки А, В, С, Д на рис. 2). Соединив эти точки, получают исходный прямоугольник АВСД.  Рис. 2 Построение координатной сетки Для того чтобы теодолитный ход разместился в средней части чертежа, положение координатных линий рассчитывают. Для этого стороны АВ и АД исходного прямоугольника делят примерно пополам, получают точки a и b. С точностью до целых метров вычисляют координаты этих точек по формулам: ха = (хmax + хmin):2 , уb = (уmax+ уmin):2 , где хmax, хmin, уmax, уmin – наибольшие и наименьшие значения координат точек хода. По данным табл.1 получим: ха = (570 +346):2 = 458 м, уb = (420 + 191):2 = 306 м . Вычисляют расстояния Δх, Δу от точек a и b до ближайших южной (нижней) и западной (левой) координатных линий, кратных 200м: Δх = 458 – 400 = 58 м, или 29 мм в масштабе 1:2000, Δу = 306 – 200 = 106 м, или 53 мм в масштабе 1:2000. Расстояние Δх откладывают от точки а к югу (вниз), а Δу – от точки b к западу (влево), накалывают точки с и d, через которые пройдут искомые координатные линии. Для точного построения координатных линий берут измерителем отрезок Ас, откладывают его от точки Д по стороне ДС исходного прямоугольника и накалывают точку с′. Через точки с и с′ проводят горизонтальную координатную линию, абсцисса которой в нашем примере равна 400м. Затем получают точку d′, откладывая измерителем отрезок Аdот точки В вдоль стороны ВС. Через точки d и d′ проводят вертикальную координатную линию, ордината которой равна 200 м. От точек с и с′, d и d′ с помощью измерителя и масштабной линейки откладывают отрезки по 10 см и получают положение остальных координатных линий. Для контроля измеряют диагонали полученных квадратов и прямоугольников. Расхождение двух диагоналей в каждой фигуре не должно превышать 0,2 мм. Точки пересечения всех координатных линий накалывают. Все дальнейшие построения выполняют от этих наколов. На координатных линиях надписывают их абсциссы и ординаты. 2.3. Нанесение точек теодолитного хода Построение точек хода выполняют с помощью измерителя и точной линейки от ближайших линий координатной сетки. Для упрощения работы в тетради составляют табл. 2 подготовки данных. В неё выписывают координаты точек, округленные в пределах точности масштаба, т.е. в пределах 0,1 мм  2000 = 0,2 м. 2000 = 0,2 м.Сначала определяют квадрат (или прямоугольник) координатной сетки, в котором располагается наносимая точка, а затем на сторонах этой фигуры откладывают отрезки, равные разностям координат точки и координатной линии. Для достижения наибольшей точности следует выбрать кратчайший путь построения. Таблица 2 Подготовка данных для построения точек хода
Пример: точка 3 расположена в прямоугольнике пткd(рис. 2) координатной сетки. Величину 26,7 мм откладывают вниз дважды: от точки п по линии пd и от точки т по линии тк. Полученные точки е и fсоединяют прямой, на которой от точки f влево откладывают отрезок 27,5 мм. Получив на плане первые две точки, проверяют правильность их нанесения. Для этого измеряют длину линии между точками и сравнивают её с записанной в ведомости вычисления координат (табл. 1). Расхождение не должно превышать 0,3 мм. Таким же образом проверяют правильность нанесения всех последующих точек хода. Если расхождение превышает допуск, проверяют правильность нанесения точек, правильность построения координатной сетки, правильность откладывания равных отрезков на полудиагоналях, т.е. проверяют все этапы построения координатной сетки и точек хода. Результаты контроля заносят в таблицу 3: Таблица 3 Контроль правильности построения точек хода
допуск 0,3 мм  Журнал съёмки с точки 3
Рис. 3 Абрис и журнал съёмки с точки 3 2.4. Построение контурных точек и составление плана Построение контурных точек выполняют по данным абриса и журнала съемки (рис. 3) с помощью линейки, транспортира, угольника. Рекомендуемый порядок нанесения точек: - сначала следует обойти весь ход, построить точки, снятые способом пересечения линий хода с контурами; - соединив одноименные точки на линиях 2-3 и 4-1 хода, построить линию связи, ЛЭП, железную дорогу; - транспортиром построить полярные углы при точке 3 по данным журнала съемки; - по полученным с точки 3 направлениям отложить указанные в журнале расстояния; - построить контур кустарника, положение первых столбов; - провести проселочную дорогу, построить остальные столбы по указанным на абрисе расстояниям между ними, нанести переезд; - способом перпендикуляров построить здания. После проверки преподавателем правильности нанесения точек хода и ситуации производят окончательное оформление плана карандашом или гелевой ручкой. Предварительно следует внимательно изучить образцы, вывешенные в лабораториях кафедры. Условные знаки наносят на план с соблюдением их размеров и начертания согласно действующим «Условным знакам для топографических планов масштабов 1:5000, 1:2000, 1:1000 и 1:500» [1]. Образцы условных знаков приведены в табл. 4. Размеры в этой таблице даны в миллиметрах. Надписи на планах располагают параллельно южной и северной рамке. Внутренней рамкой плана служит исходный прямоугольник АВСD, от сторон которого отступают по 14 мм и стоят внешнюю рамку плана. Толщина линий внешней рамки 1,2 мм. Пересечение координатных линий на плане показывают зеленым цветом. Пример вычерчивания рамки плана и зарамочного оформления показан на рис. 4. Абсциссы и ординаты координатных линий выписывают в километрах. Стороны теодолитного хода на плане не показывают. Номера точек хода располагают слева от точки. Размеры строчных букв в пояснительных надписях пород деревьев, пашни и цифр в пояснительных надписях леса принимают равным 1,5 мм, цифр в номерах геодезических и их отметках – 2 мм, в этажности зданий – 3 мм. Размер строчных букв в зарамочном оформлении 2 мм, заглавных букв – 3 мм, высота цифр в численном масштабе – 4 мм, высота букв заголовка работы – 6 мм.  Рис. 4 Пример оформления плана  Приложение 1 Исходные данные для контрольной работы №1 координаты х1 , у1 первой точки хода х1 =450,00 у1= 510,00 дирекционный угол α1-2 первой (начальной) стороны хода
Индивидуальные для каждого студента исходные данные - дирекционный угол α1-2 первой (начальной) стороны хода , которая выбирает из таблицы по первой букве фамилии и последней цифре шифра студента. Например, студент Михайлов Е.Ю. , шифр 00-С-465 выбирает задание по варианту М-5. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
