математика. 3. Зададим целевую функцию
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
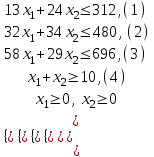 3. Зададим целевую функцию: F(X) = 4x1 + 3x2 → max Построим область допустимых решений задачи. Для этого в прямоугольной декартовой системе координат построим прямую l1: 13x1+24x2=312, соответствующую ограничению (1). Для этого найдем координаты двух точек, принадлежащих данной прямой. Полагаем x1=0, тогда x2 = 13, возьмем x2 = 0, получаем x1=24. Получили координаты точек В (24, 0) и С (0, 13). Определим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого подставим, например, координаты точки О (0; 0), не лежащей на прямой l1, в данное ограничение: 13·0 + 24·0 ≤ 312. Получаем 0 ≤ 312, следовательно точка О лежит в полуплоскости решений. Укажем данную полуплоскость штриховкой (рис.1). 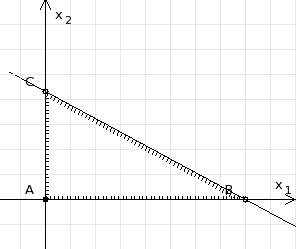 рис. 1 Аналогично строим прямую l2: 32x1+32x2 = 480, соответствующую ограничению (2) , находим полуплоскость решений. Отметим штриховкой общую часть полуплоскостей решений (рис. 2). 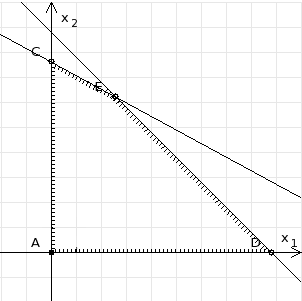 рис. 2 Строим прямую l3: 58x1 + 29x2 = 696, соответствующую ограничению (3), находим полуплоскость решений. Штриховкой обозначим общую часть полуплоскостей решений (рис. 3). 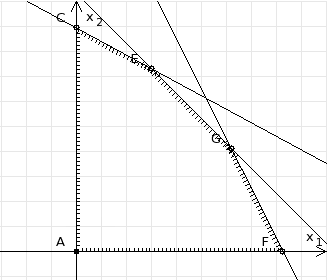 рис. 3 Построим прямую l4: x1+x2 = 10. Определим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (4). Для этого подставим, например, координаты точки О (0; 0), не лежащей на прямой l4, в данное ограничение. Получаем 0 ≥ 10, следовательно точка О не принадлежит полуплоскости решений. Штрихуем ту часть плоскости относительно прямой, где не лежит точка О. Далее находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных. Полученную область допустимых решений отметим штриховкой (рис. 4). 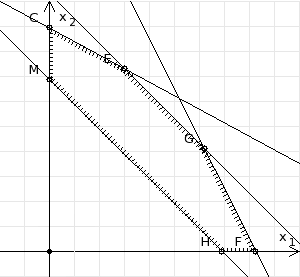 рис. 4 Построим нормаль линий уровня 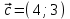 и одну из линий, например 4x1 + 3x2 = 0. и одну из линий, например 4x1 + 3x2 = 0.Так как решается задача на нахождение максимума целевой функции, то линию уровня перемещаем в направлении нормали до последней точки многоугольника решений MCEGF (рис. 5). 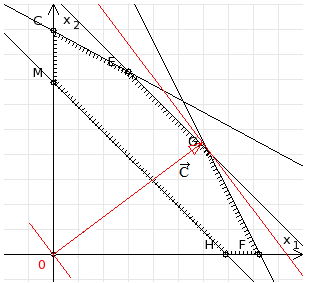 рис. 5 Видим, что последней точкой данного прямоугольника будет точка G. В данной точке значение функции будет наибольшим. Для нахождения координат точки G = l2 ∩ l3 необходимо решить систему уравнений 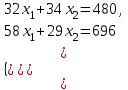 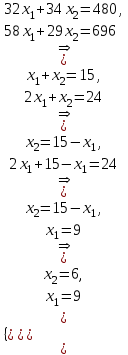 Получим G(9, 6). Находим F(G) = 4·9 + 3·6 = 54. Ответ: Для получения максимальной прибыли 54 усл. ед, необходимо производить 9 изделий вида I и 6 изделий вида II. Задание 2. В цехе работают шесть мужчин и четыре женщины. Наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины и четыре мужчины. Решение: Событие А= {среди отобранных ровно три женщины}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно выбрать 7 человек из всех работников, цеха, т.е. из 10 человек. 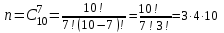 Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди 7 отобранных ровно 3 женщины): трёх женщин можно выбрать из четырёх 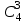 способами; при этом остальные 4 человека должны быть мужчинами. Выбрать же четырех мужчин из шести мужчин можно способами; при этом остальные 4 человека должны быть мужчинами. Выбрать же четырех мужчин из шести мужчин можно 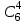 способами. способами. Следовательно, 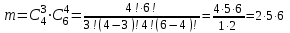 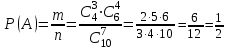 Задание3. Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый вопрос, рана 0,9; на второй – 0,7; на третий – 0,8. Найти вероятность того, что студент ответит: а) только на один вопрос б)в хотя бы на один вопрос (варианты 3,4,6) Решение: Пусть событие 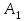 = {студент ответил на первый вопрос}, = {студент ответил на первый вопрос},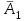 = {студент не ответил на первый вопрос}, = {студент не ответил на первый вопрос},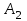 ={ студент ответил на второй вопрос }, ={ студент ответил на второй вопрос },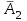 ={ студент не ответил на второй вопрос }, ={ студент не ответил на второй вопрос },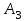 ={ студент ответил на третий вопрос }, ={ студент ответил на третий вопрос },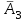 ={ студент не ответил на третий вопрос }. ={ студент не ответил на третий вопрос }.События 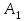 и и 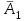 – противоположные, поэтому – противоположные, поэтому 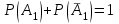 , , 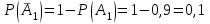 . Аналогично . Аналогично 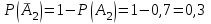 и и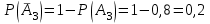 . .а) Событие 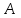 ={студент ответил только на один вопрос}. ={студент ответил только на один вопрос}.Появление события А означает, что наступило одно из трёх несовместных событий: либо 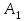 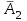 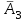 , либо , либо 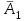 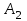 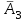 , либо , либо 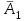 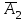 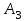 . По правилу сложения вероятностей . По правилу сложения вероятностей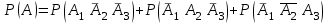 . События . События 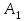 , , 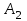 , , 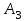 - независимые, следовательно, независимы и события - независимые, следовательно, независимы и события 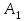 , , 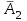 , , 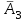 . По правилу умножения вероятностей для независимых событий . По правилу умножения вероятностей для независимых событий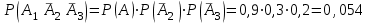 . . Аналогично 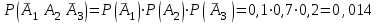 , , 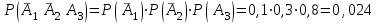 . .Тогда 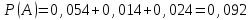 . .б) Событие В ={ студент ответил хотя бы на один вопрос }. Это означает, что был дан ответ на любой один вопрос, или на любые два вопроса, или на все три вопроса. Событие 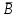 = {студент не ответил ни на один вопрос}. События B и = {студент не ответил ни на один вопрос}. События B и 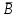 противоположны, поэтому противоположны, поэтому 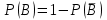 . Событие . Событие 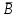 означает, что одновременно появились независимые события означает, что одновременно появились независимые события 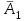 , ,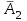 и и 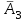 , т. е. , т. е. 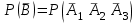 . По правилу умножения вероятностей для независимых событий . По правилу умножения вероятностей для независимых событий 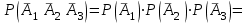 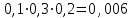 . . Итак, 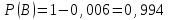 . .Варианты домашней контрольной работы Вариант №7 1. Для обработки поделочных камней используются три вида оборудования (1;2;3). Изготовляются два вида брошей из малахита и агата. Малахит обрабатывается на 1;2;3 оборудовании - 0,5;0,2;0,1 часа соответственно, агат - соответственно,0,4;0,4;0 час. Общий фонд полезного рабочего времени оборудования, соответственно составляет 40;28;6 час . Каков оптимальный план выпуска малахитовых и агатовых брошей, если цена броши из малахита 1000 руб, ., а из агата - 800 руб; а) Записать математическую модель задачи. б) Решить задачу графическим методом. ме ограничений: 0.4x2≤40, 0.2x1+0.4x2≤28 0.1x1≤6 x1 ≥ 0, x2 ≥ 0, Построим область допустимых решений, т.е. решим графически систему неравенств. Составим математическую модель задачи. 1. Введем переменные задачи: х1 –изделия из малахита; x2 – изделия из агаты ; Необходимо найти максимальное значение целевой функции F = 1000x1+800x2 → max, при системе ограничений: 0.4x2≤40, 0.2x1+0.4x2≤28 0.1x1≤6 x1 ≥ 0, x2 ≥ Составим математическую модель задачи. 1. Введем переменные задачи: х1 –изделия из малахита; x2 – изделия из агаты ; Необходимо найти максимальное значение целевой функции F = 1000x1+800x2 → max, при системе ограничений: 0.4x2≤40, 0.2x1+0.4x2≤28 0.1x1≤6 x1 ≥ 0, x2 ≥ Решение: Сведем данные в таблицу
Составим математическую модель задачи. Введем переменные задачи: х1 –изделия из малахита; x2 – изделия из агата; Необходимо найти максимальное значение целевой функции F =1000x1+800x2 → max, при системе ограничений: 0.4x2≤40, 0.2x1+0.4x2≤28 0.1x1≤6 x1 ≥ 0, x2 ≥0 Построим область допустимых решений, т.е. решим графически систему неравенств. 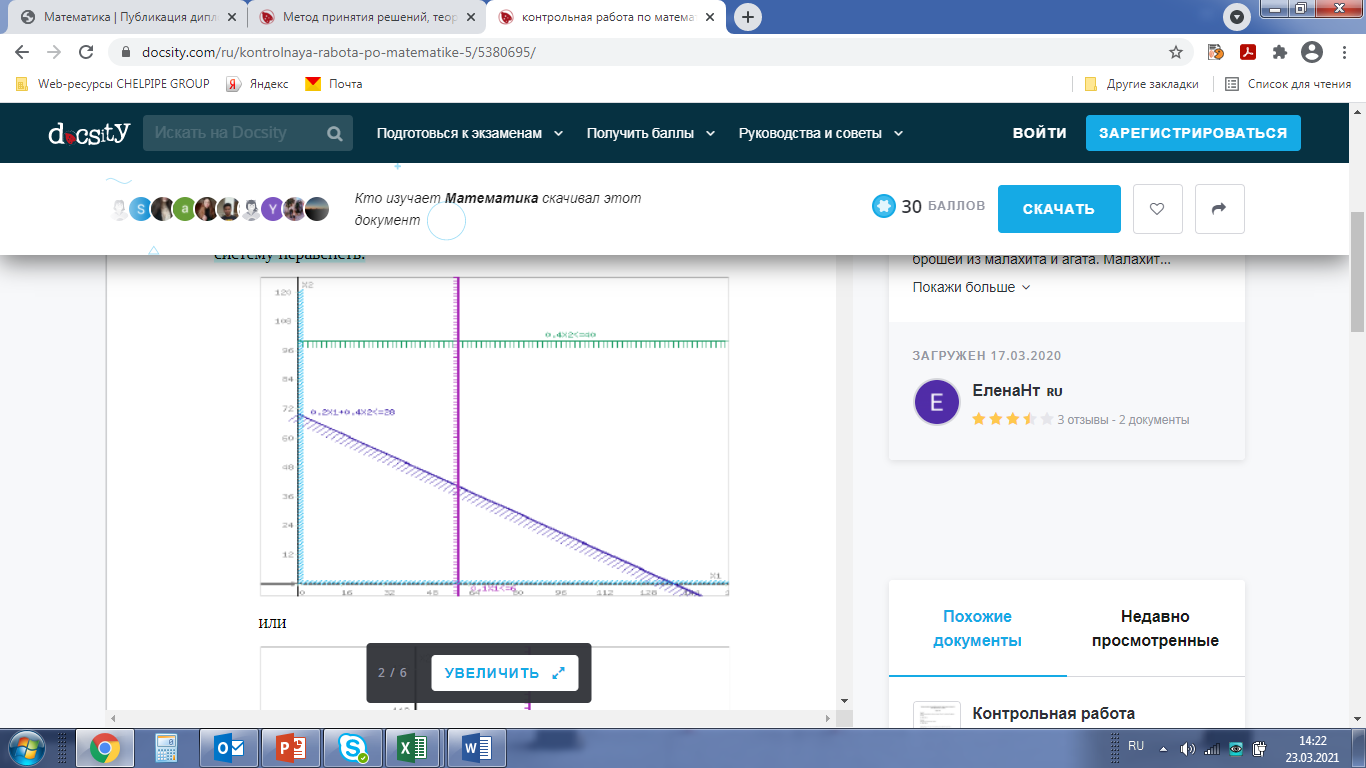 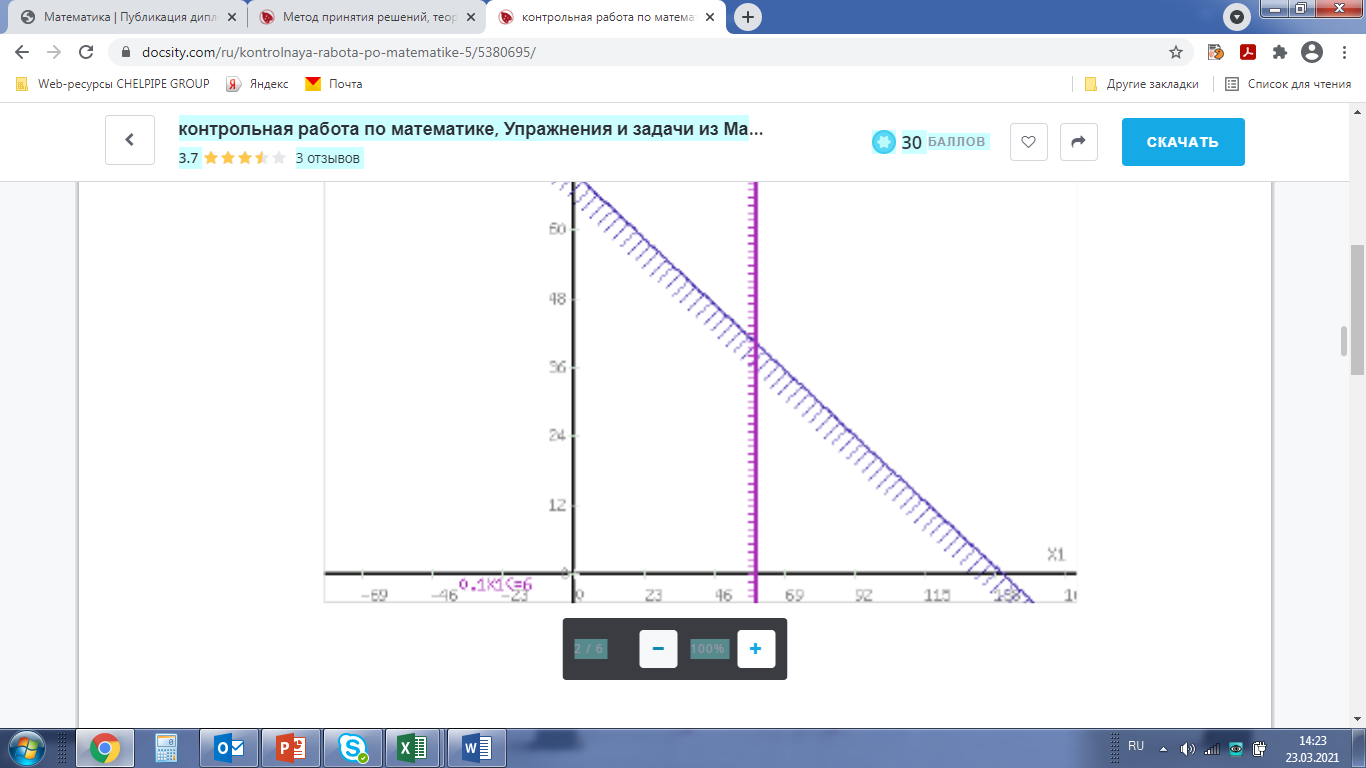 Задача 2 Три стрелка производят по одному выстрелу по обшей мишени. Вероятность попадания в мишень для первого стрелка равна 0,7; для второго 0,5; для третьего 0,8. Найти вероятность того, что будет ровно два попадания в мишень. q1=1-0,7=0,3; q2=1-0,5=0,5; q3=1-0,8=0,2 Вероятность того, что два стрелка попали в мишень. P(2) = p1*p2*q3 + p1*q2*p3 + q1*p2*p3 = 0.7*0.5*0.2 + 0.7*0.5*0,8 + 0,3*0,5*0,8 = 0,47 Ответ: Вероятность того, что будет ровно два попадания в мишень P(2) =0,47 Задание 3. Турист, заблудившись в лесу, вышел на полянку, от которой в разные стороны ведут 5 дорог. Если турист пойдет по первой дороге, то вероятность выхода туриста из леса в течении часа составляет 0,6, если по второй – 0,3, если по третей – 0,2, если по четвертой – 0,1, если по пятой – 0,1. Какова вероятность того, что турист пошел по первой дороге, если через час он вышел из леса? Решение: В данном случае событие A – «турист через час он вышел из леса» произошло. Искомая вероятность того, что турист пошел по первой дороге, если через час он вышел из леса, равна P(H1 / A) = P(H1 )P(A/ H1 ) ,∑i5=1 P(Hi )P( A/ Hi ) где Hi – гипотеза «турист через час он вышел из леса»турист пойдет по i-й дороге, i = 1, 2, 3, 4, 5. Очевидно, что все пять гипотез равновероятны, т.е. P(H1 ) = P(H2 ) = P(H3 ) = P(H4 ) = P(H5 ) = 0,2 . Значения условных вероятностей даны в условии задачи: P(A / H1 ) = 0,6; P(A / H2 ) = 0,3; P( A / H3 ) = 0,2; P( A / H4 ) =0,1; P(A / H5 ) = 0 ,1. P(H1 / A) = (0,2 х 0,6) / (0,2х0,6 +0,2х 0,3 +0,2х 0,2 +0,2х 0,1+0,2х 0,1) = 0,462 Ответ: Вероятность того, что турист пошел по первой дороге и через час вышел из леса равна. P(H1/A) = 0,462  | ||||||||||||||||||||||||||||
