Статистика. Вариант 1. сданная статистика. 1. Предмет и метод статистики. Сводка и группировка
 Скачать 101.15 Kb. Скачать 101.15 Kb.
|
КОНТРОЛЬНАЯ РАБОТА по дисциплине «Статистика» Вариант 1
Екатеринбург 2021 г. СОДЕРЖАНИЕ
Тема 1. Предмет и метод статистики. Сводка и группировка. Задача 1. Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.
Построить вариационный, ранжированный, дискретный ряд распределения, обозначив элементы ряда. Решение: Данная совокупность представляет собой множество вариантов количества получаемых студентами книг. Подсчитаем число таких вариантов и упорядочим в виде вариационного ранжированного и вариационного дискретного рядов распределения. Таблица 1 - Ранжированный вариационный ряд распределения
Таблица 2 - Дискретный вариационный ряд распределения
Тема 2. Абсолютные и относительные величины Задача 1. В таблице приведены данные о продажах автомобилей в одном из автосалонов города за 1 квартал прошедшего года. Определите структуру продаж.
Решение: Структура продаж определяется удельным весом отдельной группы в общем объеме продаж по формуле: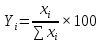 То есть, для того, что бы рассчитать структуру продаж необходимо разделить число проданных автомобилей каждой марки, на общее количество проданных автомобилей и выразить результат в процентах. Skoda: (245/1145) ×100 = 21,40 % Hyundai: (100/1145) ×100 = 8,73 % Daewoo: (125/1145) ×100 = 10,92 % Nissan: (274/1145) ×100 = 23,93 % Renault: (231/1145) ×100 = 20,17 % Kia: (170/1145) ×100 = 14,85 % Таким образом, наибольший удельный вес в общем объеме продаж автомобилей занимает марка Nissan – 23,93%, наименьший – марка Hyndai – 8,73%.Тема 3. Средние величиныЗадача 3. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов. Решение: Для определения среднего удельного веса студентов, обучающихся на коммерческой основе, используем формулу средней арифметической взвешенной: 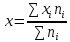 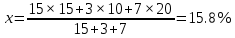 Определим количество студентов, обучающихся на коммерческой основе: УрФУ: 15 000/100 * 15 = 2 250 человек. УрГЭУ: 3 000/100 * 10 = 300 человек. УрГЮИ: 7 000/100 * 20 = 1 400 человек. Итого, обучающихся на коммерческой основе: 2 250 + 300 + 1 400 = 3 950 человек. Таким образом, общее число студентов, обучающихся на коммерческой основе, составляет 3,95 тыс.чел., или 15,8% от общего количества студентов в ВУЗах. Тема 4. Показатели вариацииЗадача 1 При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:
Определить: для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада; средний размер вклада за месяц для двух банков вместе. Дисперсию вклада для 2-х банков, зависящую от рекламы; Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы; Общую дисперсию используя правило сложения; Коэффициент детерминации; Корреляционное отношение. Решение: Для определения среднего размера вклада за месяц найдем середины интервалов. Таблица 3 - расчетная таблица для банка с рекламой.
Средний размер вклада найдем по формуле средней арифметической взвешенной: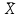 = = 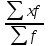 = 29 000/50 = 580 руб. = 29 000/50 = 580 руб.Дисперсию вклада найдем по формуле:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Размер месячного вклада, руб | Число вкладчиков (f) | Середина интервала (x) | xf | 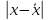 | 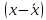 2 2 | 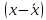 2f 2f |
| До 500 | 3 | 490 | 1 470 | 52.8 | 2 787. 84 | 8 363.52 |
| 500-520 | 4 | 510 | 2 040 | 32.8 | 1 075.84 | 4 303.36 |
| 520-540 | 17 | 530 | 9 010 | 12.8 | 163.84 | 2 785.28 |
| 540-560 | 15 | 550 | 8 250 | 7.2 | 51.84 | 7 776.00 |
| 560-580 | 6 | 570 | 3 420 | 27.2 | 739.84 | 4 439.04 |
| 580-600 | 5 | 590 | 2 950 | 47.2 | 2 227.84 | 11 139.20 |
| 600-620 | - | 610 | - | - | - | - |
| 620-640 | - | 630 | - | - | - | - |
| Итого | 50 | - | 27 140 | - | - | 31 808 |
Средний размер вклада:
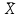 =
=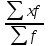 = 27 140/50 = 542,8 руб.
= 27 140/50 = 542,8 руб.Дисперсия вклада:
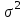 =
=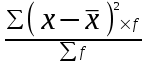 = 31 808/50 = 636,2
= 31 808/50 = 636,22) Найдем средний размер вклада для двух банков вместе. Хср =(580×50+542,8×50)/100 = 561,4 руб.
3) Дисперсию вклада, для двух банков, зависящую от рекламы найдем по формуле: σ2=pq (формула дисперсии альтернативного признака). Здесь р=0,5 – доля факторов, зависящих от рекламы; q=1-0,5, тогда σ2=0,5*0,5=0,25.
4) Поскольку доля остальных факторов равна 0,5, то дисперсия вклада для двух банков, зависящая от всех факторов кроме рекламы тоже 0,25.
5) Определим общую дисперсию, используя правило сложения.
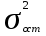 =
=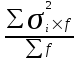 = (468*50+636,16*50)/100=552,08
= (468*50+636,16*50)/100=552,08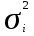 =
=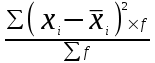 = [(580-561,4) 250 + (542,8-561,4) 250] / 100 = 34 596/ 100 = 345,96
= [(580-561,4) 250 + (542,8-561,4) 250] / 100 = 34 596/ 100 = 345,96 Общая дисперсия: 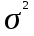 =
=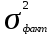 +
+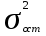 = 552,08+345,96 = 898,04
= 552,08+345,96 = 898,04
6) Коэффициент детерминации: 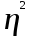 =
=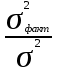 = 345,96/898,04 = 0,39 = 39% - размер вклада на 39% зависит от рекламы.
= 345,96/898,04 = 0,39 = 39% - размер вклада на 39% зависит от рекламы.
7) Эмпирическое корреляционное отношение:
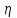 =
=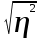 =
=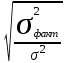 =
= 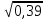 = 0,62 – связь достаточно тесная.
= 0,62 – связь достаточно тесная.
Это свидетельствует об умеренной зависимости средней величины от факторов положенных в основу.
Тема 5. Выборочное наблюдение
Задача 1.
Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:
| Группы предприятий по объему продукции, тыс. руб. | Число предприятий (f) |
| 1 | 2 |
| До 100 100-200 200-300 300-400 400-500 500 и > | 28 52 164 108 36 12 |
| итого | 400 |
Определить: 1) по предприятиям, включенным в выборку: а) средний размер произведенной продукции на одно предприятие; б) дисперсию объема производства; в) долю предприятий с объемом производства продукции более 400 тыс. руб.; 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать: а) средний объем производства продукции на одно предприятие; б) долю предприятий с объемом производства продукции более 400 тыс. руб.; 3) общий объем выпуска продукции по области.
Решение:
Таблица 5 – Расчетная таблица
Группы предприятий по объему продукции, тыс. руб. | Число предприятий (f) | Середина интервала (x) | xf |
|
До 100 | 28 | 50 | 1 400 | 70 000 |
100-200 | 52 | 150 | 7 800 | 1 170 000 |
200-300 | 164 | 250 | 41 000 | 10 250 000 |
300-400 | 108 | 350 | 37 800 | 13 230 000 |
400-500 | 36 | 450 | 16 200 | 7 290 000 |
500 и > | 12 | 550 | 6 600 | 3 630 000 |
Итого | 400 | - | 110 800 | 35 640 000 |
По предприятиям, включенным в выборку, средний размер произведенной продукции на одно предприятие:
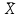 =
=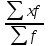 = 110 800/400 = 277
= 110 800/400 = 277
Дисперсию объема производства вычислим упрощенным способом σ2 = 35 640 000/400 – 2772 = 89 100 – 76 229 = 12 371.
Число предприятий, объем производства продукции которых превышает 400 000 руб. равно 36 + 12 = 48, а их доля равна ω = 48:400 = 0,12 = 12%.
Из теории вероятности известно, что при вероятности Р=0,954 коэффициент доверия t=2. Предельная ошибка выборки:
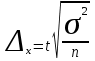 = 2
= 2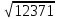 / 400 = 11,12 тыс. руб.
/ 400 = 11,12 тыс. руб.
Установим границы генеральной средней: 277-11,12 ≤Хср≤ 277+11,12; 265,88 ≤Хср≤ 288,12
Предельная ошибка выборки доли предприятий:
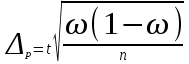 = =2
= =2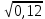 * 0,88/400 = 0,03
* 0,88/400 = 0,03
Определим границы генеральной доли: 0,12-0,03≤ р ≤0,12+0,03; 0,09≤ р ≤0,15
Поскольку рассматриваемая группа предприятий составляет 10% от общего числа предприятий области, то в целом по области насчитывается 4000 предприятий.
Тогда общий объем выпуска продукции по области лежит в пределах 265,88×4000≤Q≤288,12×4000; 1063520 ≤ Q ≤ 1152480
Тема 6. Ряды динамики
Задача 1.
Данные о площадях под картофелем до и после изменения границ района, тысяч гектаров:
периодыплощадьпод картофелем | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
До изменения границ района | 110 | 115 | 112 | ----- | ----- | ----- | ----- |
После изменения границ района | ----- | ----- | 208 | 221 | 229 | 234 | 230 |
Сомкнутый ряд | 204.2 | 213.5 | 320 | 221 | 229 | 234 | 230 |
Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района.
Решение:
Примем за базу сравнения третий период – период, за который есть данные как в прежних, так и в старых границах района. Затем эти два ряда с одинаковой базой смыкаем в один.
Определим коэффициент соотношения площадей до изменения границ района и после:
208/112=1,857 – коэффициент
Пересчитаем площадь первых двух периодов на новые границы
110*1,857=204.27
115*1,857=213.55
115/112*100=102,68%
110/112*100=98,21%
221/208*100=106,25%
229/208*100=110,096%
234/208*100=112,5%
230/208*100=110,58%
Таблица 6
периоды | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
До изменения границ района | 110 | 115 | 112 | ----- | ----- | ----- | ----- |
После изменения границ района | ----- | ----- | 208 | 221 | 229 | 234 | 230 |
3 период – 100% | 98,21 | 102,68 | 100 | - | - | - | - |
- | - | 100 | 106,25 | 110,1 | 112,5 | 110,58 | |
Сомкнутый ряд относительных величин в % к 3 периоду | 98,21 | 102,68 | 100 | 106,25 | 110,1 | 112,5 | 110,58 |
Сомкнутый ряд | 204.2 | 213.5 | 208 | 221 | 229 | 234 | 230 |
Тема 7. Экономические индексы
Задача 7
По нижеприведенным данным ответить на вопросы, поставленные в таблице, т.е. определить недостающие показатели.
Показатели | Изменение показателей в % к предыдущему кварталу «+»-увеличение, «-» - уменьшение | ||
II квартал | III квартал | IV квартал | |
Цена | ? | +10 | -2 |
Натуральный объем продаж | Без изменения | ? | +5 |
Товарооборот в денежном выражении | +8 | +5 | ? |
Решение:
1) ІІ квартал: Ip= ?; Iq= 1; Ipq =1,08; Ip = Ipq/Iq = 1,08:1 = 1,08 (в таблицу поместим +8).
2) ІІІ квартал: Ip = 1,1; Iq = ?; Ipq =1,05; Iq = Ipq/Ip = 1,05:1,1 = 0,95 (в таблицу поместим -5).
3) ІV квартал: Ip =0,98; Iq = 1,05; Ipq =?; Ipq = Ip×Iq = 0,98×1,05 = 1,029 ≈ 1,03 (в таблицу поместим +3).
Таблица 7 - Изменение показателей по отношению к предыдущему кварталу
Показатели | Изменение показателей в % к предыдущему кварталу «+»-увеличение, «-» - уменьшение | ||
II квартал | III квартал | IV квартал | |
Цена | +8 | +10 | -2 |
Натуральный объем продаж | Без изменения | -5 | +5 |
Товарооборот в денежном выражении | +8 | +5 | +3 |
Тема 8. Основы корреляционного анализа
Задача 1.
По пяти рабочим цеха имеются данные о квалификации и месячной выработке. Для изучения связи между квалификацией рабочих и их выработкой определить линейное уравнение связи и коэффициент корреляции. Дать интерпретацию коэффициентам регрессии и корреляции.
| Табельный номер рабочего | Разряд | Выработка продукции за смену, шт. |
| 1 2 3 4 5 | 6 2 3 5 4 | 130 60 70 110 90 |
Решение:
Расширим предлагаемую таблицу.
| Табельный номер рабочего | Разряд, X | Выработка продукции за смену, шт., Y | X2 | XY | Y2 |
| 1 2 3 4 5 | 6 2 3 5 4 | 130 60 70 110 90 | 36 4 9 25 16 | 780 120 210 550 360 | 16 900 3 600 4 900 12 100 8 100 |
| Итого: | 20 | 460 | | 2020 | 45 600 |
Определим параметры уравнения прямой yx = a + bx. Для этого решим систему уравнений:
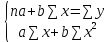
n = 5
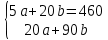
5a + 20 b = 460
a + 4b = 92
a = 92 - 4b
20 (92-4b) + 90b = 2 020
1840 – 80b + 90b = 2 020
1840 + 10b = 2 020
10b = 2 020 – 1840
10b = 180
B = 18
Коэффициент регрессии равен 18.
Поскольку b - положительное число, то имеется прямая связь между параметрами x и у.
а=92-4×18
а=20
Линейное уравнение связи имеет вид ух=20+18х.
Для определения тесноты (силы) связи между изучаемыми признаками определим величину коэффициента корреляции по формуле:
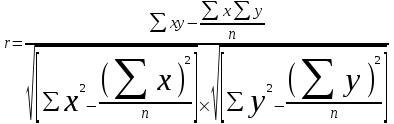
= (2020-20×460/5)/(√10×√3280) ≈ 180/181,11=0,99.
Поскольку коэффициент корреляции больше 0,7, то связь в данном ряду сильная.
Тема 9. Статистический анализ социально-экономического развития общества
Задача 1.
Имеются следующие данные за 2006 год:
численность населения, тыс чел.: на 1 января - 430,0; на 1 апреля - 430,2; на 1 июля 430,3; на 1 октября - 430,7; на 1 января 2007 г. 430,8
. число умерших, чел. - 8 170
. число выбывших на постоянно жительство в другие населенные пункты, чел. - 570
. коэффициент жизненности - 1,075
. доля женщин в общей численности населения, % - 58
. доля женщин в возрасте 15-49 лет в общей численности женщин, % - 39
Определите: коэффициенты рождаемости, смертности, естественного, механического и общего прироста населения; число родившихся; число прибывших на постоянно жительство из других населенных пунктов; специальный коэффициент рождаемости.
Решение:
Определим по формуле средней хронологической среднюю численность населения за 2006 год:
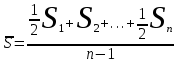 =
=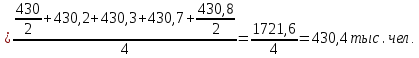
Число родившихся в 2006 году определим через коэффициент жизненности как:
N = Kжизн × M = 1,075 × 8170 = 8 783 чел.
Коэффициент рождаемости равен:
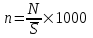 =
= 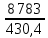 × 1000 = 20,4 %
× 1000 = 20,4 %Коэффициент смертности равен:
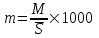 =
= 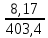 × 1000 = 19 %
× 1000 = 19 %Коэффициент естественного прироста равен:
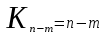 = 20,4 – 19 = 1,4 %
= 20,4 – 19 = 1,4 %Известно, что
НКГ = ННГ + N – M + П – В.
Отсюда получим число прибывших на постоянно жительство из других населенных пунктов:
П = НКГ – ННГ – N + M + В = 430,8 – 430 – 8,783 + 8,17 + 0,57 = 0,757 тыс. чел.
Коэффициент механического прироста населения равен:
Кмех.пр. =
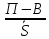 × 1000 =
× 1000 = 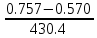 × 1000 = 0.43 %
× 1000 = 0.43 %Коэффициент общего прироста населения равен:
Кобщ.пр. = Кест.пр. + Кмех.пр. = 1,4 + 0,43 = 1,73 %.
Специальный коэффициент рождаемости равен:
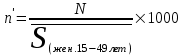 =
= 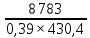 × 1000 = 52,3 %
× 1000 = 52,3 %Таблица 8
| Коэффициент рождаемости | 20,4% |
| Коэффициент смертности | 19% |
| Коэффициент естественного прироста населения | 1,4% |
| Коэффициент механического прироста населения | 0,43% |
| Коэффициент общего прироста населения | 1,73% |
| Число родившихся;; | 8 783 чел. |
| Число прибывших на постоянное место жительство из других населенных пунктов | 757 чел. |
| Специальный коэффициент рождаемости. | 52,3% |
Тема 10. Статистика рынка труда и занятости населения
Задача 1.
Имеются данные на конец года по РФ, млн. чел.:
- численность населения – 146,7
- экономически активное население – 66,7
- безработных, всего - 8,9, в том числе
зарегистрированных в службе занятости – 1,93.
Определить: 1) уровень экономически активного населения; 2) уровень занятости; 3) уровень безработицы; 4) уровень зарегистрированных безработных; 5) коэффициент нагрузки на 1 занятого в экономике.
Решение:
Уровень экономически активного населения равен доле численности экономически активного населения в общей численности населения:
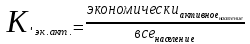 =
= 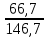 = 0,4547 (45,47%)
= 0,4547 (45,47%)Уровень занятости равен:
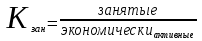 =
= 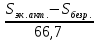 =
= 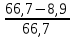 = 0,8666 (86,66%)
= 0,8666 (86,66%)Уровень безработицы равен:
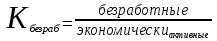 =
= 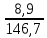 = 0,0607 (6,07%)
= 0,0607 (6,07%)Уровень зарегистрированных безработных равен:
Кзар.безр. =
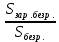 =
= 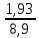 = 0,2169 (21,69%)
= 0,2169 (21,69%)Коэффициент нагрузки на 1 занятого в экономике равен:
Кнагр =
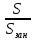 =
= 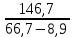 = 2,538.
= 2,538.Таблица 9
| Уровень экономически активного населения | 45,47% |
| Уровень занятости | 86,6% |
| Уровень безработицы | 6,07% |
| Уровень зарегистрированных безработных | 21,69% |
| Коэффициент нагрузки на 1 занятого в экономике | 2,538 |
Список использованных источников
Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики, информатики, финансов и права. - М., 2003;
Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика» для студентов экономических специальностей: УрГЭУ, 2007;

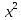 f
f