Биомеханика физических упражнений ( PDFDrive ) — копия. 1. предмет и методы биомеханики
 Скачать 239.62 Kb. Скачать 239.62 Kb.
|
|
Коэффициенты Bi, для вычисления центрального момента инерции сегментов тела (по данным В.М. Зациорского и др., 1981)
Используя табличные данные коэффициентов уравнений множественной регрессии, можно вычислить центральный момент инерции сегментов тела че ловека относительно его фронтальной оси, что соответствует положению рас сматриваемой модели тела спортсмена при выполнении, к примеру, оборото вых упражнений на перекладине. Отдельные звенья модели, состоящие из сегментов, также имеют цен тральный момент инерции, определяемый относительно оси, проходящей через центр масс звена. Правомерно возникает вопрос о способе его вычисления. С этой целью можно воспользоваться одним из положений теоретической меха ники: если известна величина момента инерции тела относительно какой-либо оси, то можно определить момент инерции данного тела и относительно любой другой оси, параллельной заданной и расположенной на произвольном рассто янии от нее. В математической форме данная зависимость выражается в виде соотношения Jo = Jc + mr 2, (4.21) где Jo – момент инерции тела относительно заданной оси; Jc – централь ный момент инерции; m – масса тела; r – расстояние от заданной оси до центра масс тела. 75 Рассмотрим технологию определения центрального момента для звеньев тела, состоящих из отдельных сегментов, например, для ноги, включающей в себя три сегмента: бедро, голень, стопу. Для иллюстрации воспользуемся ри сунком 4.9, на котором показана кинематическая схема ноги. Поместим ось тазобедренного сустава в начало системы координат и обо значим кружками суставы с соответствующими значениями координат по осям Ох, Оу: X1, Y1 – координаты тазобедренного сустава; X2, Y2 – координаты колен ного сустава; Х3, У3 – координаты голеностопного сустава. YL L L 3 1 2 S S S 1 2 3 ОХ Хс Х Хс Х Хс Х 1 1 2 2 Рис. 4.9. Кинематическая схема ноги 3 3 Координатами центра масс сегментов тела будут соответственно: 1. Xc1, Yc1 – координаты центра масс бедра; 2. Хс2, Yc2 – координаты центра масс голени; 3. Хс3, Ус3 – координаты центра масс стопы. Положим, что координаты как центра масс сегментов так и суставов по оси Оу равны нулю. Воспользуемся данными выполненных расчетов и припишем для масс сегментов, их длин и положений центра масс следующие значения: бедро – m1 = 9,921; L1 = 44; S1 = 23,19; голень – m2 = 2,999; L2 = 38; S2 = 15,36; стопа – m3 = 0,951; L3 = 26, S3 = 13,927. Согласно рис. 4.9 координаты центра масс бедра, голени, стопы соответ ственно равны Xc1 = 23,19; Xc2 = 59,36; Хс3 = 91,927. Введем обозначения для центральных моментов инерции сегментов ноги относительно оси Oz, перпендикулярной плоскости чертежа и проходящей че- 76 рез центры масс сегментов: J1 – центральный момент инерции бедра; J2 – цен тральный момент инерции голени; J3 – центральный момент инерции стопы. Численные значения Ji соответственно равны: J1 = 1822,2; J2 = 328,13; J3 = 40,02. На основании уравнений (4.18), (4.21) получим величину момента инерции ноги (Jo) относительно оси Oz, проходящей через тазобедренный сустав, пер пендикулярно плоскости чертежа (рис. 4.9) Jo = J1+ m1 (Xc1) 2 + J2 + m2 (Xc2) 2 + J3 + m3 (Хс3) 2. (4.22) В то же время Jo = Jc + m (Xc) 2, где Jc – центральный момент инерции ноги; m – масса ноги; Хс – расстояние от центра масс ноги до оси Oz. Для определения центрального момента инерции биомеханической систе мы (Jc) воспользуемся уравнением Штейнера и приведем его к виду Jc = Jo - mr2, (4.23) где m – масса биомеханической системы; r – расстояние от ОЦМ системы до оси вращения, проходящей через точку опоры. Учитывая, что r = Xc и принимая во внимание уравнение (4.22) для рас сматриваемой трехзвенной модели имеем Jc = J1 + J2 + J3 + m1 (Xc1)2 + m2 (Xc2) 2 + m3 (Хс3) 2- m (Xc) 2, (4.24) или в численном значении при m = 13,871 и Хс = 35,722818 получим, что Jc = 8428,3712. Для модели звена, состоящей из N сегментов, выражение (4.24) имеет вид N N = + − ∑ ∑ 2 2 Jc J m Xc mXc . i i i i i = = 1 1 Как видно из уравнений (4.22), величина момента инерции тела определя ется его массой и квадратом расстояния от центра масс тела до оси вращения. В 77 процессе выполнения упражнений масса тела спортсмена остается постоянной, а расстояние от центра масс звеньев тела до оси вращения, проходящей через точку опоры, меняется. Действительно, тело человека представляет собой био механическую систему переменной конфигурации, поэтому в динамических упражнениях взаимное расположение звеньев тела носит переменный характер, а следовательно, изменяется и расстояние от центров масс звеньев тела до точ ки опоры, что влечет за собой и изменение величины момента инерции как от носительно оси, проходящей через ОЦМ тела спортсмена, так и относительно оси, проходящей через точку опоры. Рассмотрим вопрос об определении момента инерции трехзвенной биомеханической системы относительно оси, проходящей через точку опоры при произвольных, анатомически допустимых углах, между звеньями тела (рис. 4.10). 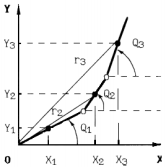 Рис. 4.10. Момент инерции трехзвенной биомеханической системы Обозначим через X1, X2, Х3 – координаты центра масс первого, второго и третьего звена по оси Oх и соответственно через Y1, Y2, Y3 – по оси Оу. Расстояния от начала системы коор динат, помещенной в точку опоры, до центра масс первого, второго и третьего звена обозна чим через r1, r2, r3. В этом случае момент инерции рассматриваемой трехзвенной системы относительно оси Oz, проходящей через начало системы координат Oxyz перпендикулярно плоскости рисунка, согласно (4.19), (4.22) определяется из выражения Jo = J1 + m1r12 + J2 + m2r22 + J3 + m3r32. (4.25) Так как r12 = X12 + Y12, r22 = Х22 + Y22, r32 = Х32 + Y32, 78 а координаты центра масс звеньев (Xi, Yi) выражаются в свою очередь через длины звеньев тела (Li), обобщенные координаты (Qi) и положение центра масс звеньев относительно оси шарниров (Si), то соответственно имеем r12 = S12cos2Q1 + S12sin2Q1; r22 = L12cos2Q1 + 2L1S2cosQl cos Q2 + S22cos2Q2 + + L12sin2Q1 + 2L1 S2 sinQ1sinQ2 + S22sin2Q2; r32 = L12 cos2Q1 + L22cos2Q2 + S32cos2Q3 + + 2L1L2cosQlcosQ2 + 2L1S3 cosQlcosQ3 + 2L2 S3 cosQ2cosQ3 + + L12sin2Q1 + L22sin2Q2 + S32sin2Q3 + + 2L1L2sinQ1sinQ2 + 2L1S3sinQ1sinQ3 + 2L2S3sinQ2sinQ3. Выполнив соответствующие преобразования, получим r12 = S12; r22 = L12 + 2L1S2 cos(Q2-Q1) + S22; r32 = L12 + L22 + S32 + 2L1L2 cos(Q2-Q1) + 2L1S3 cos(Q3 - Q1) + + 2L2S3 cos(Q3 - Q2). Подставляя полученные значения ri в уравнения (63), получим соотношение вида Jo = A11+ А22 + А33 + + 2A12 cos(Q2-Q1) + 2A13 cos(Q3-Q1) + 2А23 соs(Q3 - Q2), (4.26) где коэффициенты Aij равны: А11 = J1 + m1S12 + L12 (m2 + m3); A12 = L1 (m2S2 + m3 L2); A13 = m3S3L1; (4.27) A22 = J2 + m2S22 + m3 L22; A23 = m3S3L2; А33 = J3+ m3S32. Таким образом, момент инерции биомеханической системы относительно оси, прохо дящей через точку опоры перпендикулярно плоскости движения, определяется динамиче скими характеристиками звеньев тела (Aij) и обобщенными координатами системы. Уравне ние (4.26) позволяет, при известных значениях коэффициентов Aij и заданных значениях обобщенных координат, определить Jo для трехзвенной биомеханической системы любой конфигурации. Аналитическое выражение момента инерции для N-звенной биомеханической системы построим при условии введения в формульную запись для коэффициентов Аij символа Кро некера. Символ Кронекера равен 79 |
