Биомеханика физических упражнений ( PDFDrive ) — копия. 1. предмет и методы биомеханики
 Скачать 239.62 Kb. Скачать 239.62 Kb.
|
|
4. БИОМЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ 4.1. Классификация биомеханических характеристик Исследуя движения человека, измеряют количественные показатели: − механического состояния и двигательной функции тела; − пространства состояний биомеханической системы (движений). Механическое состояние и двигательные функции тела человека описы ваются большим набором характеристик (размеры, пропорции, распределение масс сегментов и звеньев тела человека, подвижность в суставах, величина си лы тяги мышц и др.). Механическое состояние биомеханической системы в движении также описывается определенными характеристиками (пространственное положение, скорость, ускорение, координаты и траектория отдельных звеньев биомехани ческой системы и общего центра масс тела человека, кинетическая и потенци альная энергия и др.). Биомеханические характеристики – это меры механического состояния и изменения биосистемы. Для системного анализа (определения состава системы) движений биоме ханические характеристики позволяют различать разные движения, отличить одно движение от другого. Для системного синтеза (определение структуры движения) биомеханиче ские характеристики дают возможность установить закономерность измене ния движений под воздействием различных факторов. Иначе говоря, выяснить, например, как влияет последовательность и величина (амплитуда) сгибательно разгибательных движений в суставах или их отсутствие на формирование тра ектории биомеханической системы? Или, каким образом изменится траектория биомеханической системы при увеличении ее динамических ресурсов, к приме ру, на 10%, 20%, 30%, а программное управление кинематического уровня останется без изменений? Когда биомеханические характеристики измеряют или вычисляют, то по лучают количественные характеристики, с помощью которых выполняют ко личественный биомеханический анализ исследуемых движений. 54 Когда характеристики описывают только словами (без измерения), то это – качественные характеристики. Педагогу во время проведения урока некогда и нечем измерять и регистрировать количественные характеристики и поэтому он обычно проводит качественный биомеханический анализ движений. Для описания движения в пространстве и во времени используют кинема тические характеристики. Кинематические характеристики описывают внешнюю картину движения, его пространственную форму (рисунок, узор) и характер изменения во времени (быстрее, чаще и т.п.). Кинематические харак теристики включают три группы характеристик: − пространственные; − временные; − пространственно-временные. Кинематические характеристики, определяя геометрию движения, не учи тывают движущиеся массы и действующие силы и поэтому не в состоянии дать ответ на вопрос о причинах возникновения и изменения движений. Причины возникновения и изменения движений раскрывает динамика с использованием динамических характеристик, включающих в себя три большие группы биоме ханических характеристик: − силовые; − инерционные; − энергетические. Биомеханические характеристики двигательных действий, включающие в себя структурные компоненты кинематических и динамических характеристик, показаны на рисунке 4.1. БИОМЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КИНЕМАТИЧЕСКИЕ ДИНАМИЧЕСКИЕ Пространст венные Времен ные Пространствен но-временныеСиловые Инерционные Энерге тические Рис. 4.1. Классификационная схема биомеханических характеристик 55 Резюмируя все вышесказанное, можно дать следующую обобщенную классификацию биомеханических характеристик: 1. Качественные характеристики. 2. Количественные характеристики. 3. Характеристики сегментов и звеньев тела человека. 4. Характеристики движений: − кинематические характеристики; − динамические характеристики. 4.2. Биомеханические характеристики сегментов тела человека Для биомеханических расчетов динамических характеристик исследуемых упражнений необходимы данные о масс-инерционных характеристиках (МИХ) сегментов тела человека, т.к. соответствующие уравнения динамики включают в себя те или иные численные значения, характеризующие геометрию масс тела человека. В биомеханике под геометрией масс тела человека понимается мас сив показателей, характеризующий распределение массы, как всего тела, так и его отдельных сегментов. Такими показателями являются массы, положение центра масс сегментов, моменты инерции, длины сегментов. Так, например, общий центр масс биомеханической системы является од ной из масс-инерционных характеристик, наиболее широко используемых при исследовании техники соревновательных упражнений. Определение траектории движения ОЦМ тела спортсмена имеет большое значение при исследовании вопросов сохранения устойчивого равновесия в приземлении после выполнения соскоковых упражнений в гимнастике, оптимизации движений, построения эф фективной программы места и позы спортсмена в динамических упражнениях и в ряде других случаях. В частности, по траектории движения ОЦМ определяют эффективность решения двигательных задач в упражнениях, связанных с вра щением тела относительно закрепленной оси, так как увеличение или уменьше ние скорости вращательного движения тела спортсмена определяется измене нием радиуса вращения ОЦМ тела спортсмена. Для определения положения ОЦМ биомеханической системы необходимо знать масс-инерционные характеристики сегментов тела человека и уметь 56 определять общий центр масс системы тел, моделирующих различную конфи гурацию звеньев тела спортсмена в подводящих и соревновательных упражне ниях. Часто в учебно-методической и научной литературе можно встретить по нятие о центре тяжести тела. Возникает вопрос: тождественны ли понятия «центр масс тела» и «центр тяжести тела»? Здесь следует сделать пояснение. В любом случае центр масс тела совпадает с координатами его центра тяжести, если тело находится в однородном поле сил тяготения. Действительно, обозна чим символами P1, Р2, Р3, Р4 силы, действующие на отдельные частицы тела, а их равнодействующую – символом Р (рис. 4.2). В этом случае вес тела равен модулю равнодействующей и определяется равенством Р = P1 + Р2 +. . .+ Рn. Если мысленно повернуть тело относительно любой оси пространственной системы координат, то силы Pi остаются приложенными в одних и тех же точ ках параллельными друг другу и сохраняют направление. Таким образом, рав нодействующая Р сил Рi при любых положениях тела будет проходить через одну и ту же точку С, называемую центром тяжести тела. x zp1 2 3 4 p p p p Рис. 4.2. Равнодействующая сил Следовательно, центр тяжести твердого тела есть неизменно связанная с этим телом точка, через которую проходит связанная с этим телом линия дей ствия равнодействующих всех сил тяжести частиц данного тела при любом его 57 положении в пространстве. Этой точкой также будет определяться и центр масс тела. Таким образом, понятие центра тяжести имеет смысл только в том случае, если тело находится в однородном поле силы тяжести. Для любой же системы материальных тел, для которых равнодействующая всех внешних сил равна ну лю, правомерно употребление понятия, центр масс. К примеру, в условиях не весомости имеет смысл говорить о центре масс тела, а не о центре тяжести. В условиях же действия поля силы тяжести эти два понятия не имеют принципи ального различия, хотя понятие о центре масс тела в этом случае все же более корректно. В математической модели движения человека, представленной в виде си стемы дифференциальных уравнений второго порядка, в качестве постоянных коэффициентов при угловых (обобщенных) скоростях и ускорениях звеньев модели используют динамические коэффициенты. Численная величина дина мических коэффициентов зависит от 4-х параметров сегментов тела человека: 1) длина сегмента (кинематическая характеристика – пространственная). 2) координата центра масс сегмента (кинематическая характеристика – пространственная). 3) масса сегмента (динамическая характеристика – инерционная). 4) момент инерции сегмента (динамическая характеристика – инерцион ная). В различных формульных выражениях для вычисления кинематических или динамических характеристик упражнений эти четыре параметра, в той или иной мере, также всегда имеют место. Поэтому важно знать их количественные показатели и уметь численно определить. В соответствии с первым законом Ньютона всякое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения до тех пор, по ка внешние приложенные к телу силы не заставят его изменить это состоя ние. Иначе говоря, тело сохраняет свою скорость, а также под действием внеш них сил изменяет ее. В этом проявляется свойство инертности физических тел: противодействовать изменению скорости. Чем больше инертность, тем труднее тело сдвинуть с места или затормозить его. 58 Масса – это мера инертности тела при поступательном движении. Масса (m) измеряется отношением приложенной силы (F) к вызываемому силой уско рению (a) m = aF. (4.1) Измерение массы по формуле (4.1) основано на втором законе Ньютона: изменение движения пропорционально извне действующей силе и происходит по тому направлению, по которому эта сила приложена. В процессе выполнения различных упражнений масса спортсмена не изме няется. При взвешивании определяется вес (Р) спортсмена в килограммах (кг). В этом случае из формулы (4.2) следует, что массу (m) спортсмена можно опре делить как m = gP. (4.2) Здесь: g – ускорение свободного падения тела, равное 9,806 м/с2. Размер ность массы – кг с2/м. Центр масс сегмента. Биомеханический анализ техники соревнователь ных упражнений подразумевает учет не только величины массы, но и ее рас пределение в сегменте тела – центр масс сегмента, точки – совпадающей с точкой центра тяжести этого же сегмента (в условиях действия силы тяже сти). Момент инерции – это мера инертности тела во вращательном движе нии. Момент инерции (J) прямо пропорционален массе тела (m) и квадрату рас стояния (r) от центра масс тела до оси вращения J = mr2. (4.3) В основном, в биомеханических исследованиях, достаточно знать парамет ры следующих сегментов тела человека: кисть, предплечье, плечо, туловище, голова, бедро, голень, стопа. Длина сегмента, как известно из курса анатомии, определяется расстояни ем от центра суставов, ограничивающих данный сегмент, и измеряется антро пометрическим циркулем. Единица размерности длины – метр. 59 Остальные три параметра определяются экспериментальным или аналити ческим методами. Аналитические методы определения геометрии масс тела человека. Определение координаты центра масс однородного стержня не представляет затруднений: расположение искомой точки определяется половиной длины стержня. Сегменты тела человека не являются стержнями, и координата их цен тра масс приближена или удалена от суставов, его ограничивающих. Поэтому, числено координаты центра масс сегментов тела человека, можно определить или по средне-статистическим данным, или по уравнениям множественной ре грессии. Средне-статистические данные, являются одним из тех показателей, кото рые позволяют достаточно просто определить координаты центра масс тела че ловека: вес сегмента или расположение его центра масс составляет определен ный процент от веса тела человека или от длины его сегмента. Например, вес кисти составляет 1% от веса тела человека, или, расстояние от плечевого суста ва до центра масс предплечья равно 43% от длины предплечья. Недостаток данной методики – недостаточная точность получаемых результатов: погреш ность может достигать 50% – 70%. Уравнения множественной регрессии позволяют определить биомеханиче ские характеристики сегментов тела человека с учетом веса и роста испытуе мых. Коэффициенты в уравнениях множественной регрессии определены ста тистическими методами на основе радиоизотопной методики определения гео метрии масс тела человека. Погрешность использования алгоритмов уравнений множественной регрессии не превышает 3%. Экспериментальное определение Так как тело человека представляет собой биомеханическую систему, со стоящую из связанных сегментов, то прижизненное экспериментальное опреде ление их масс-инерционных характеристик связано со значительными трудно стями. Первые экспериментальные данные о геометрии масс тела человека бы ли получены зарубежными исследователями (Harless, 1860; Braune, Fisher, 1889 и др.). Сегменты тела замороженных трупов рассекались по осям вращения су ставов, затем взвешивались, и экспериментально определялись координаты центра масс сегментов и их моменты инерции. Полученные данные до недавне- 60 го времени являлись практически единственными, на основе которых выполня лись расчеты по динамике двигательных действий человека. В настоящее время потребность в повышенной точности выполнения био механических расчетов привела к необходимости получения более точной ин формации о геометрии масс тела человека. И одним из наиболее корректных методов прижизненного определения масс-инерционных характеристик тела человека, позволяющим получить искомые характеристики с достаточной точ ностью, является радиоизотопный метод. В лаборатории ГЦОЛИФК кафедры биомеханики (Зациорский В.М., Аруин А.С., Селуянов В.Н., 1981) проблема практической реализации идеи радиоизотопного метода была успешно решена. В серии проведенных экспериментов были получены уточненные данные о масс-инерционных характеристиках сегментов тела человека. В таблице 4.1 приведены сведения об относительных весах (m%) и коор динатах центра масс сегментов (ЦМ%) на их продольных осях. В результате экспериментальных исследований были установлены относительные весовые коэффициенты (m%), определяющие с точностью не менее 3,7% массу сегмен тов тела в процентах к массе тела в целом. Точность – достаточная для биоме ханических исследований и педагогических рекомендаций. Т а б л и ц а 4.1 Относительные веса и координаты центра масс сегментов
Зная массу тела и используя относительные весовые коэффициенты, мож но определить абсолютную массу сегмента тела спортсмена по формуле 61 mi= (m·m%i) /100, где m – масса тела спортсмена; mi – масса i-го сегмента. Аналогичным образом определяются и координаты центра масс сегментов на их продольной оси. Отсчет расстояния при этом выполняется от антропо метрической точки сегмента (рис. 4.3). Простота и доступность вычислений геометрии масс тела человека с по мощью весовых и относительных коэффициентов создает предпосылки для широкого внедрения этого метода в биомеханические расчеты. Однако, для бо лее полного учета индивидуальных особенностей строения опорно двигательного аппарата тела человека, авторами разработанной радиоизотоп ной методики определения геометрии масс тела человека, предложено исполь зовать уравнения множественной регрессии. Дело в том, что взаимосвязь между весом сегмента и весом тела, между относительным расстоянием от антропометрической точки сегмента до его цен тра масс и длиной сегмента не может быть выражена уравнением вида Y=AX, Где Y – вес сегмента или положение его центра масс; А – весовой или от носительный коэффициенты; Х – вес или длина сегментов тела. Результаты определения геометрии масс тела человека с помощью радио изотопной методики свидетельствуют о том, что даже в простейшем случае ис комая связь имеет вид Y = А0 + A1X1. Исследования, выполненные авторами, позволили им вывести уравнения множественной регрессии для оценки массы сегментов тела и положения их центров масс, учитывающие антропометриче ские особенности испытуемых. В табл. 4.2 приведены коэффициенты уравне ний множественной регрессии для вычисления массы сегментов тела и положе ния центра масс сегментов по двум аргументам: по массе и длине тела. Положение центра масс и масса сегмента определяются по формуле Y = АО + A1X1 + A2X2, где X1 – масса тела; Х2 – длина тела; A0, A1, A2 – коэффициенты уравнений мно жественной регрессии. 62 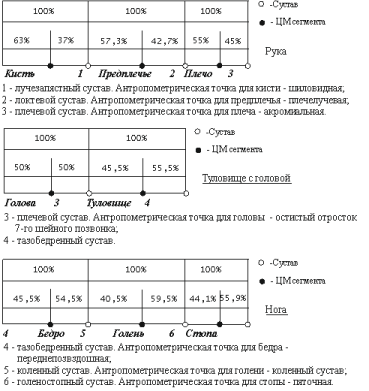 Рис. 4.3. Антропометрические точки сегментов тела человека Рис. 4.3. Антропометрические точки сегментов тела человека Т а б л и ц а 4.2 |
