геодезия все ответы. 1. предмет и задачи геодезии

• Название: 1. предмет и задачи геодезии
• Анкор: геодезия все ответы.docx
• Дата: 27.01.2018
• Размер: 212.44 Kb.
• Имя файла: геодезия все ответы.docx
• Тип: Документы; #14957
• страница: 2 из 4

Теодоли́т — измерительный прибор для определения направлений и измерения горизонтальных и вертикальных углов при геодезических работах, топографических, геодезических и маркшейдерских съёмках, в строительстве и т. п. Основной рабочей мерой в теодолите являются лимбы (горизонтальный и вертикальный круги с градусными и минутными делениями). Конструктивно теодолит состоит из следующих основных узлов: Корпус с горизонтальным и вертикальным отсчетными кругами, и др. технологическими узлами; Подставка (иногда употребляют термин «трегер») с тремя подъёмными винтами и круглым уровнем(для горизонтирования теодолита); Зрительная труба; Наводящие и закрепительные винты для наведения и фиксации зрительной трубы на объекте наблюдения; Цилиндрический уровень Оптический центрир (отвес) для точного центрирования над точкой ,Отсчетный микроскоп для снятия отсчетов. Горизонтальный круг теодолита предназначен для измерения горизонтальных углов и состоит из лимба и алидады. Лимб представляет собой стеклянное кольцо, на скошенном крае которого нанесены равные деления с помощью автоматической делительной машины. Цена деления лимба (величина дуги между двумя соседними штрихами) определяется по оцифровке градусных (реже градовых) штрихов. Оцифровка лимбов производится по часовой стрелке от 0 до 360 градусов (0 — 400 гон). Роль алидады выполняют специальные оптические системы — отсчётные устройства. Алидада вращается вокруг своей оси относительно неподвижного лимба вместе с верхней частью прибора; при этом отсчёт по горизонтальному кругу изменяется. Если закрепить зажимной винт и открепить лимб, то алидада будет вращаться вместе с лимбом и отсчёт изменяться не будет. Лимб закрывается металлическим кожухом, предохраняющим его от повреждений, влаги и пыли. в России предусматривается выпуск шести типов теодолитов:
Т1 — высокоточные
Т2 и Т5 — точные
Т15 и Т30 — технические
Т60 — технические (в настоящее время не выпускается) Литера Т — обозначает «теодолит», а последующие числа — величину средней квадратической погрешности в секундах, при измерении одним приёмом в лабораторных условиях. Обозначение теодолита, изготовленного в последние годы может выглядеть так: 2Т30МКП. В данном случае первая цифра показывает номер модификации («поколения»). М — маркшейдерское исполнение (для работ в шахтах или тоннелях; может крепиться к потолку и использоваться без штатива, помимо этого, в маркшейдерском теодолите в поле зрения визирной трубы есть шкала для наблюдения за качаниями отвеса при передаче координат с поверхности в шахту). К — наличие компенсатора, заменяющего уровни. П — зрительная труба прямого видения, то есть зрительная труба теодолита имеет оборачивающую систему для получения прямого (не перевернутого) изображения. А — с автоколлимационным окуляром (автоколлимационные); Э — электронные.

11.Поверки теодолита. Поверками теодолита называют действия, имеющие целью выявить, выполнены лигеометрические условия, предъявляемые к инструменту. Для выполнения нарушенных условий производят исправление, называемое юстировкой инструмента. 1. Ось каждого цилиндрического уровни алидады горизонтального круга должна быть перпендикулярна к оси вращения, алидады. Это условие необходимо для приведения оси вращения инструмента (алидады) в рабочее положение, т. е. чтобы при измерениях углов она была вертикальна. Для поверки выполнения условия поворотом алидады устанавливают ось поверяемого уровня по направлению каких-либо двух подъемных винтов и одновременным вращением их в разные стороны приводят пузырек уровня в нульпункт (на середину ампулы), тогда ось уровня займет горизонтальное положение. Повернем алидаду, а вместе с нею и уровень точно на 180. Если после приведения пузырька уровня в нульпункт и поворота алидады на 180° пузырек уровня останется на месте, то условие выполнено. Для выполнения других поверок необходимо привести прибор в рабочее положение. 2. Одна из нитей сетки должна находиться в вертикальной плоскости. Поверку и юстировку этого условия можно выполнить при помощи отвеса, установленного в 5—10 м от инструмента. Если поверяемая нить сетки не совпадет с изображением отвеса в поле зрения трубы, то снимают колпачок, слегка ослабляют (примерно на полоборота) четыре винта, крепящих окулярную часть с корпусом трубы, и поворачивают окулярную часть с сеткой до требуемого положения. Закрепляют винты и надевают колпачок. После юстировки вторая нить сетки должна быть горизонтальна. Убедиться в этом можно, наведя эту нить на какую-либо точку и вращая алидаду наводящим винтом по азимуту; нить при этом должна оставаться на данной точке. В противном случае юстировку надо повторить. Установив правильно сетку, в дальнейшем при повторении поверок эту можно не повторять. 3. Визирная ось должна быть перпендикулярна к оси вращения зрительной трубы. Это условие необходимо для того, чтобы при вращении трубы вокруг ее оси визирная ось описывала плоскость, а не конические поверхности. Визирную плоскость называют также коллимационной. Вертикальный круг вращается вокруг оси вместе с трубой. Для перевода трубы из положения КП в положение КЛ или наоборот надо перевести ее через зенит при неподвижном лимбе и повернуть алидаду на глаз на 180°, чтобы можно было наводить трубу на один и тот же предмет при различных ее положениях. При этом на том месте относительно лимба, где находится верньер1 , теперь будет расположен диаметрально противоположный верньер 2 к отсчеты числа градусов, взятые по верньеру I до поворота алидады и по верньеру II после поворота алидады на 180°, должны быть одинаковы. Если визирная ось перпендикулярна к оси вращения зрительной трубы, то при наведении ее при КП и КЛ на удаленную точку , расположенную приблизительно на уровне оси вращения зрительной трубы, по закрепленному горизонтальному лимбу получим верные отсчеты дуги с помощью I (при КП) и II (при КЛ) верньеров. Если же визирная ось не перпендикулярна к оси вращения трубы и занимает при КП и при КЛ неверное положение , то в отсчеты по горизонтальному лимбу войдет ошибка, соответствующая повороту визирной оси на угол, называемый коллимационной ошибкой. Проекция этого угла на горизонтальную плоскость лимба меняется в зависимости от угла наклона визирной оси. Поэтому при выполнении этой поверки линия визирования должна быть по возможности горизонтальна. Юстировка: слабив слегка один вертикальный, например верхний, исправительный винт при сетке нитей, передвигают сетку, действуя боковыми исправительными винтами при ней до совмещения точки пересечения нитей с изображением наблюдаемой точки . После юстировки надо повторить поверку и убедиться, что условие выполнено. 4. Ось вращения зрительной трубы должна быть перпендикулярна к оси вращения инструмента (алидады). Это условие необходимо для того, чтобы после приведения инструмента в рабочее положение коллимационная (визирная) плоскость была вертикальна. Для поверки выполнения данного условия приводят инструмент в рабочее положение и направляют точку пересечения сетки нитей на высокую и близкую (на расстоянии 10—20м от инструмента) точку , выбранную на какой-нибудь светлой стене. Не поворачивая алидады, наклоняют трубу объективом вниз до примерно горизонтального положения ее оси и отмечают на той же стене точку _г, в которую проектируется точка пересечения нитей. Переведя трубу через зенит, при другом положении круга снова направляют визирную ось на ту же точку и подобно предыдущему, наклонив трубу объективом вниз, отмечают точку а₂. Если обе точки совместятся в одной точке , то условие выполнено. Выполнение рассматриваемого условия обеспечивается заводом или производится в мастерской, так как современные теодолиты не имеют соответствующих исправительных винтов.

12.Измерение длин линий в теодолитной съемке.

Над одной из крайних точек измеряемой линии устанавливается в рабочее положение теодолит ,а над другой рейка. Определяется место нуля вертикального круга теодолита. Измеряется высота прибора (от центра оси вращения трубы до поверхности земли). Визируется на отсчет по рейке,равный высоте прибора. Считываются отсчеты по крайним штрихам сетки дальномера и вертикальному кругу теодолита. Вычисляются число делений рейки, видимых между крайними штрихами сетки, и угол наклона визирной оси к горизонту. Вычисляется искомое расстояние:S=K*n*cosγ где:S –искомое расстояние в м;K-коэффициент дальномера; n-число делений рейки, видимых между крайними нитями;γ-угол наклона.

13. измерение горизонтальных углов способом приемов.

Измерение отдельного угла складывается из следующих действий: - наведение трубы на точку, фиксирующую направление первой стороны угла (рис.4.16), при круге лево (КЛ), взятие отсчета L1; - поворот алидады по ходу часовой стрелки и наведение трубы на точку, фиксирующую направление второй стороны угла; взятие отсчета L2, - вычисление угла при КЛ (рис.4.16): βл = L2 - L1, - перестановка лимба на 1o - 2o для теодолитов с односторонним отсчитыванием и на 90o - для теодолитов с двухсторонним отсчитыванием, - переведение трубы через зенит и наведение ее на точку, фиксирующую направление первой стороны угла, при круге право (КП); взятие отсчета R1, - поворот алидады по ходу часовой стрелки и наведение трубы на точку, фиксирующую направление второй стороны угла; взятие отсчета R2, - вычисление угла при КП: βп = R2 - R1, при выполнении условия |βл - βп| < 1.5 * t, где t - точность теодолита, вычисление среднего значения угла: βср = 0.5 * (βл + βп). Измерение угла при одном положении круга (КЛ или КП) составляет один полуприем; полный цикл измерения угла при двух положениях круга составляет один прием. Запись отсчетов по лимбу и вычисление угла производятся в журналах установленной формы.

14. Способы съемки ситуации в теодолитной съемки. Целью теодолитной  (горизонтальной)  съемки  является  составление контурного плана местности.  Съемка элементов  ситуации  на  местности производится относительно пунктов и сторон теодолитного хода съемочного обоснования.  На рис.40 показан абрис теодолитной съемки  по  линии 1-2 теодолитного хода.  Арабскими цифрами в кружках указаны точки, положение которых получено следующими способами съемки ситуации: 1 - прямоугольных координат; 2 - линейной засечки; 3 - угловой засечки; 4 - полярных координат; 5 - створа; 6 - обмера. При съемке способом прямоугольных координат,  положение точки 1 определено координатами Х = 72.4 м, У = 9.8 м от линии теодолитного хода 1-2.  Приложив  нулевой штрих рулетки к углу дома (точка 1),  на ленту расположенную на линии 1-2 теодолитного хода опускают перпендикуляр  и отсчитывают  его  длину  по рулетке (9.8 м),  по ленте - расстояние от пункта 1 съемочного обоснования до основания перпендикуляра (72.4  м). Перпендикуляры  длиной до 4...8 в зависимости от масштаба съемки восстанавливаются визуально,  а при использовании эккера могут быть увеличены  примерно в пять раз.  Эккер - прибор для построения на местности прямых углов. Способом линейных засечек определено положение второго угла  дома (точки 2).  Для этого на местности измерено расстояния 10.6 и 9.8 м от опорных точек на линии с абсцисами соответственно 54.1  и  64.0.  Угол дома  на плане окажется в точке пересечения дуг с радиусами измеренных расстояний. Способом угловой  засечки  на  плане может быть получена точка 3. Для этого измерены теодолитом углы 33 35' и 65 05'. Способ полярных  координат предусматривает измерение на местности (точка 4) полярного угла (70 00') и  его стороны (35.3 м). Способ створа  (вертикальная плоскость через две точки) использован при съемке точки пересечения ручьем линии теодолитного хода (точка 5). Расстояние (10.5 м) измерено по створу от пункта 1. Способ обмера элементов ситуации применяют для  контроля  полевых измерений и графических построений на плане.

15.Вычисление углов невязки и ее распределение в замкнутых теодолитных ходах. За счет возникновения ошибок сумма измеренных углов теодолит хода может отличаться от теоретич суммы углов.

Угловая невязка- разность между суммой углов практической и суммой углов теоретической

f_{β =}∑β _{изм -} ∑β _теор

∑β _{теор =}180*(n-2)- измерение внутреннего угла

∑β _{теор =}180*(n+2)- измерение внешнего угла

Невязка должна быть меньше или равна предельной величине

16.Вычисление дирекционных углов и румбов для линий теод хода по измеренным правым и левым горизонтальным углам.

Для вычисления дир углов замкнутого хода надо знать дир угол из одной стороны хода. Зная начальный дир угол и привязочные углы. Можно определить дир углы всех линий хода

При измеренном правом гор угле:

α_n =α _{n- 1} + 180- β _прав.

При измеренном левом угле:

α_n =α _{n- 1} + β _лев – 180

Румбы находятся:

0-90 СВ r= α

90-180 ЮВ r=180-α

180-270 ЮЗ r= α-180

270-360 СЗ r=360- α

17. Вычисление абсолютной и относительной линейных невязок и их распределение в замкнутом теодолитном ходе. Вычисление координат.

Линейная невязка- вычисление приращения ∆х и ∆у, содержащие в себе некоторые ошибки и их суммы отличаются от 0 на некоторую величину f

Абсолютная линейная невязка:

ƒ _s= 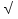ƒ_х²+ ƒ_у²

Относительная невязка:

ƒ _относ.=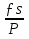, где Р- периметр хода

Вычисление координат:

По исправленным приращениям координат вычисляют координаты поворотных точек хода:

х_n= х _n-1 +∆ х _испр

у_n= у _n-1 +∆ у _испр

18.Прамая и обратная геодезические задачи.  Прямая геодезическая задачаВ геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние S_AB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.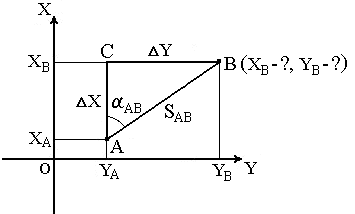



Рис. 23. Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом. Дано: Точка А( X_A, Y_A ), S_AB и α_AB. Найти: точку В( X_B, Y_B ). Непосредственно из рисунка имеем: ΔX = X_B – X_A;  ΔY = Y_B – Y_A . Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС: ΔX = S_AB · cos α_AB ; ΔY = S_AB · sin α_AB . Так как в этих формулах S_AB всегда число положительное, то знаки приращений координат ΔX  и  ΔY зависят от знаков cos α_AB  и  sin α_AB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности в которую направлена линия
	I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

При помощи румба приращения координат вычисляют по формулам: ΔX = S_AB· cosr_AB ; ΔY = S_AB· sinr_AB . Знаки приращениям дают в зависимости от названия румба. Вычислив приращения координат, находим искомые координаты другой точки: X_B = X_A +ΔX  ;  Y_B = Y_A + ΔY  . Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения. Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB (рис.24).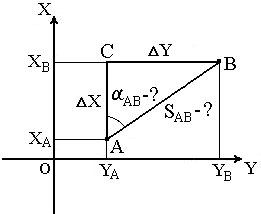



Рис. 24. Обратная геодезическая задача Даннная задача решается следующим образом. Сначала находим приращения координат:  ΔX = X_B – X_A;  ΔY = Y_B – Y_A . Величину угла r_AB определем из отношения

ΔY	= tg rAB
ΔX

 По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB. Для контроля расстояние S_AB дважды вычисляют по формулам:

SAB=	ΔX	=	ΔY	= ΔX · sec αAB = ΔY · cosec αAB
	cos αAB		sin αAB

 

SAB=	ΔX	=	ΔY	= ΔX · sec rAB = ΔY · cosec rAB
	cos rAB		sin rAB

Расстояние S_AB можно определить также по формуле

.

19.Вычисление площади полигона по координатам его вершин. Пусть требуется определить площадь полигона A₁, A₂, A₃, A₄, A₅ с координатами вершин x₁,y₁; x₂,y₂; x₃,y₃; x₄,y₄; x₅,y₅. Площадь полигона S можно представить трапециями, у которых абсциссы являются основаниями, а разности ординат соседних точек высотами

S = a₁A₁A₂a₂ + a₂A₂A₃a₃ + a₃A₃A₄a₄ - a₅A₅A₄a₄ - a₁A₁A₅a₅.
2S = (x₁ + x₂)(y₂ - y₁) + (x₂ + x₃)(y₃ - y₂) + (x₃ + x₄)(y₄ - y₃) + (x₄ + x₅)(y₅ - y₄) + (x₅ + x₁)(y₁ - y₅). (1)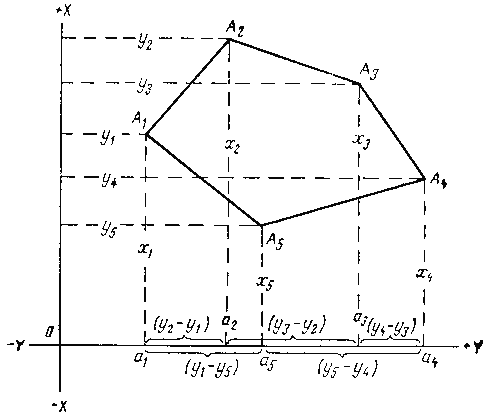



После раскрытия скобок и приведения подобных членов получим

2S = x₁y₂ - x₂y₁ + x₂y₃- x₃y₂ + x₃y₄ - x₄y₃ + x₄y₅ - x₅y₄ + x₅y₁ - x₁y₅ (2)
После вынесения за скобки x₁, x₂, x₃, x₄, x₅ будем иметь

2S = x₁(y₂-y₅) + x₂(y₃-y₁) + x₃(y₄-y₂) + x₄(y₅-y₃) + x₅(y₁-y₄)

а если из формулы (2) вынести за скобки y₁, y₂, y₃, y₄, y₅. то будем иметь

2S = y₁(x₅-x₂) + y₂(x₁-x₃) + y₃(x₂-x₄) + y₄(x₃-x₅) + y₅(x₄-x₁).

В сокращенном виде эти формулы можно записать так:





После преобразований получаем формулу в ее нормальном виде.

Аналогичное можно проделать и для любого другого многоугольника.

20.Планиметр.Определение площади. Аналитический способ. Если участок представляет собой замкнутый многоугольник, то, сняв с плана прямоугольные координаты его вершин, площадь участка вычисляют по формуле:

  ,

где i - номера вершин многоугольника, пронумерованных по ходу часовой стрелки.

По этой же формуле можно вычислить площадь с криволинейными границами, если координаты точек границы сняты так часто, что отрезки между точками можно считать прямыми. В последнем случае съём координат выполняют с помощью специального прибора – дигитайзера, а вычисления выполняют на ЭВМ.