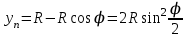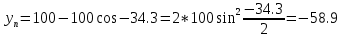пр15. Практическое задание 13
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» «Тольяттинский государственный университет»
Практическое задание №13 по учебному курсу «Геодезия» (наименование учебного курса) Вариант __ (при наличии)
Тольятти Расчетно-графическая работа №15 Построение горизонтальной кривой способом перпендикуляров Цель работы – научиться выполнять детальную разбивку кривой способом перпендикуляров (прямоугольных координат) в соответствии с требуемой точностью. Построить кривую в масштабе 1:1000 на листе бумаги. Исходные данные: значение радиуса кривой R – берутся по варианту из приложения 1. Варианты заданий выбирать по первой букве Вашей фамилии (табл.1). Таблица 1
Основные положения Для обеспечения плавного перехода с одного направления трассы на другое служат кривые. Для сопряжения двух прямых наиболее удобной кривой является круговая кривая, имеющая во всех своих точках одну и ту же кривизну и, следовательно, один и тот же радиус. Для производства расчетов и для разбивки на местности необходимо знать шесть элементов круговой кривой: угол поворота трассы θ; радиус кривой R; тангенсТ; кривую К; биссектрисуБ домер Д. 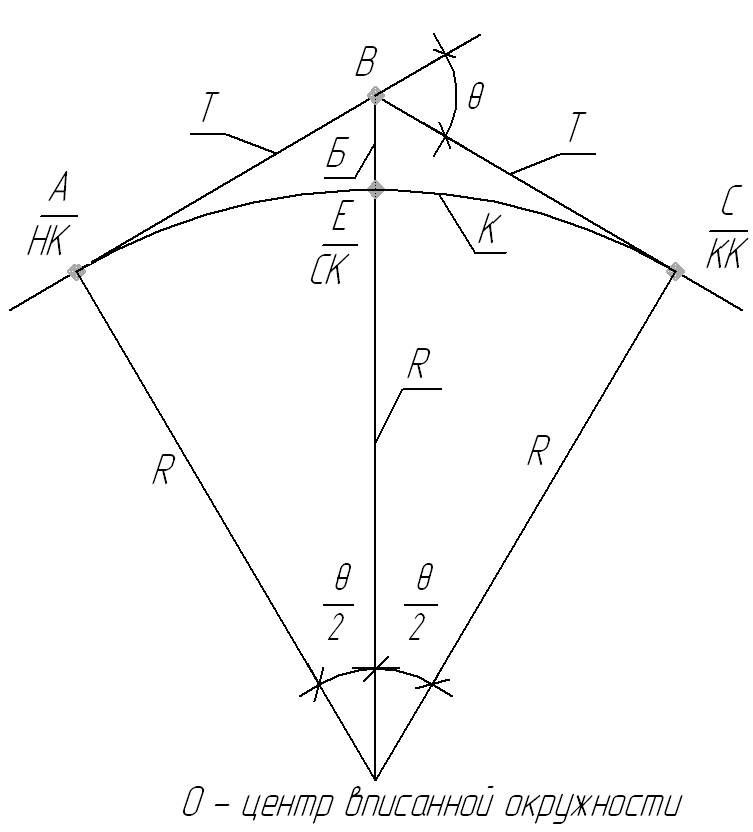 Рис.1. Схема разбивки главных точек кривой.θ – угол поворота; R – радиус кривой; Т – тангенс; К – длина кривой; Б – отрезок биссектрисы; Д – домер Угол поворота θ вычисляют по заданному горизонтальному углу. Радиус R назначают в зависимости от характера местности и технических условий проектирования линейных сооружений и зданий, имеющих закругления. Главными точками закругления являются: начало А, середина Е и конец кривой С (сокращённо НК, СК и КК). Для разбивки кривой от вершины угла поворота В необходимо отложить отрезки ВА = ВС = Т, а вдоль биссектрисы угла (180° – θ) – отрезок ВЕ. Эти отрезки обозначают соответственно черезТ и Б и называют: тангенс и биссектриса кривой. Кроме того, необходимо знать длину кривой К и величину домера Д (разность между двумя тангенсами и кривой). Вычисление элементов горизонтальной кривой По радиусу R и по величине угла поворота θ находят элементы кривой: Т (тангенс), К (кривая), Д (домер), Б(биссектриса). Элементы горизонтальной кривой вычисляют или по известным формулам, или находят по специальным таблицам для разбивки круговых кривых. Тангенс Т = 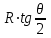 ; ;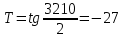 Кривая К = 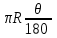 ; ; Домер Д = 2Т – К; 2 * (-27) – 6 = -60 Биссектриса Б = R(1-сos 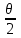 ) / cos ) / cos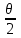 . .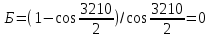 Разбивка кривой по трем главным точкам выполняют, главным образом, в период изысканий, но при постройке сооружений требуется детальная разбивка кривой. Для детальной разбивки необходимо получить ряд точек на кривой на таком расстоянии одна к другой (К = 2, 5, 10, 20 м), чтобы отрезок дуги кривой можно считать за отрезок прямой. Длина таких отрезков дуги будет зависеть от величины радиуса кривой. Чем больше радиус, тем длиннее будут и отрезки. Детальная разбивка может быть выполнена разными способами. Рассмотрим способ перпендикуляров (прямоугольных координат). Способ перпендикуляров (прямоугольных координат) Этот способ является наиболее распространенным и точным. Суть этого способа состоит в следующем. Допустим, требуется выполнить детальную разбивку кривой радиуса R, т. е. найти точки Р1, Р2, Р3,…Рn так, чтобы расстояние между ними по кривой были равны К (рис. 2). 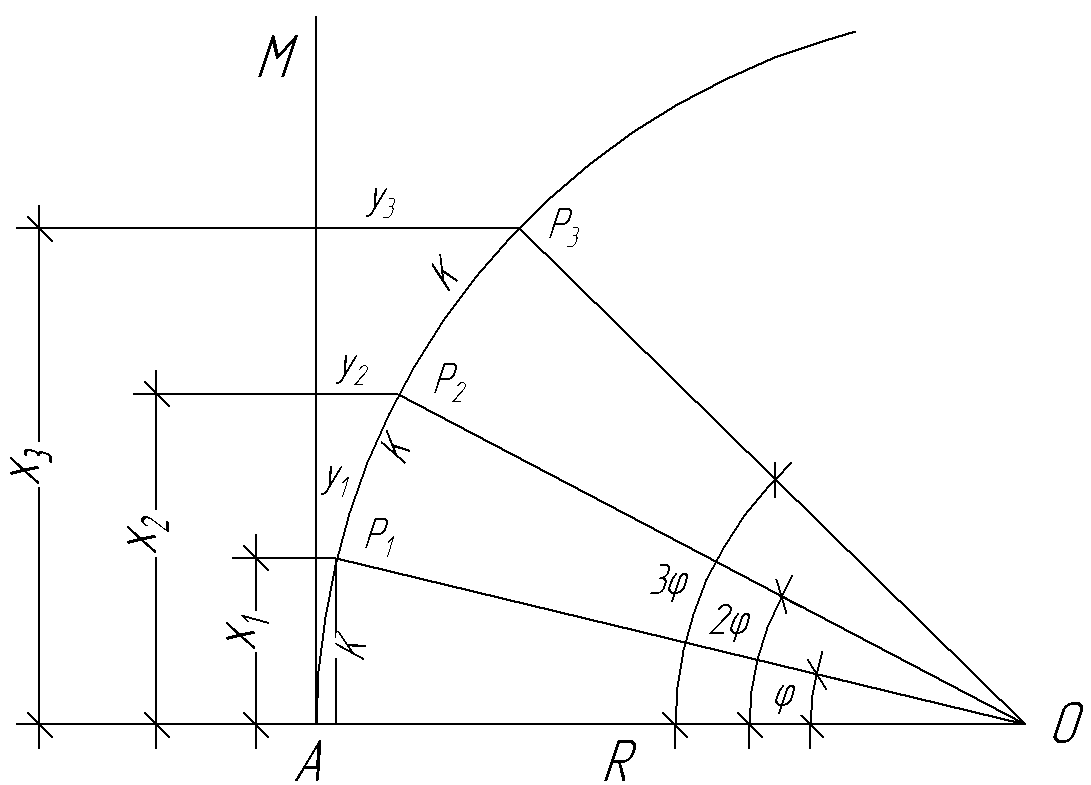 Рис. 2. Схема разбивки кривой способом прямоугольных координат Примем для этой цели, касательную АМ за ось абсцисс, а точкуА за начало счета абсцисс. Радиус R – за ось ординат. Тогда положение точек Р1, Р2, Р3,…Рn на кривой можно определить с помощью прямоугольных координат. С этой целью найдем сначала величину угла φ, соответствующего заданной дуге К(1,2,3,4, и т. д). Величина коэффициента К зависит от величин Х и У, чем меньше их значение, тем больше коэффициент.
откуда
Из рис. 2 положение точек определится отрезками х и y.
Построение кривой начинают с выбора вершины угла поворота трассы и построении тангенса АО = Т в соответствии с заданным масштабом. Разбивку кривой ведут от начала кривой и от конца кривой к середине. Начало и конец кривой – это значение тангенсов построенных от точки О. Абсциссы и ординаты откладывают соответственно по касательной АМ и перпендикулярно к ней при помощи линейки. Точки на кривой отстоят одна от другой на одинаковом расстоянии, т. к. принимают интервал разбивки К (1, 2 и т. д.).Затем последовательно соединить отложенные точки и получится кривая. Приложение 1 Значения радиусов, углов поворота трассы
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

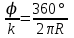 ,
, 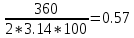
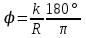
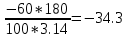
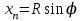 ;
;