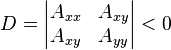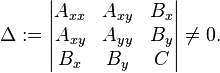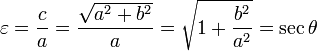Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида: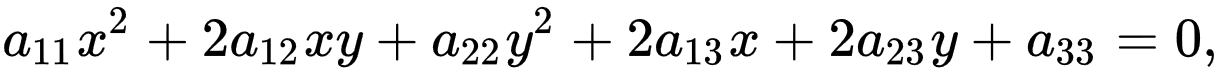 {\displaystyle a_{11}x^{2}+2a_{12}xy+a_{22}y^{2}+2a_{13}x+2a_{23}y+a_{33}=0,}в котором по крайней мере один из коэффициентов {\displaystyle a_{11}x^{2}+2a_{12}xy+a_{22}y^{2}+2a_{13}x+2a_{23}y+a_{33}=0,}в котором по крайней мере один из коэффициентов  {\displaystyle a_{11}, {\displaystyle a_{11},a_{12},
a_{22}}отличен от нуля. Таким образом кривая второго порядка является частным случаем алгебраической кривой. К ним относятся эллипс, гипербола, парабола и окружность.
История:
Впервые кривые второго порядка изучались Менехмом, учеником Евдокса. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы образованного ими угла, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII веке, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, при достижении второй космической скорости — по параболе, а при скорости, большей второй космической, — по гиперболе.
Эллипс
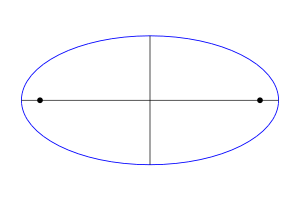
Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
| F1M | + | F2M | = 2a, причем | F1F2 | < 2a.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
1. Связанные определения
Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Точка пересечения большой и малой осей эллипса называется его центром.
Расстояния r1 и r2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
Расстояние 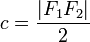 называется фокальным расстоянием. называется фокальным расстоянием.
Диаметром называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
Радиус эллипса в данной точке вычисляется по формуле 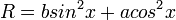 , где x - угол наклона до данной точки. , где x - угол наклона до данной точки.
Фокальным параметром 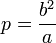 называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса. называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: 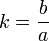 . Величина, равная . Величина, равная 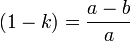 называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением 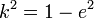
2. Свойства
Оптическое свойство. Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
Если F1 и F2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X) равен углу между этой касательной и прямой (F2X).
Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Эволютой эллипса является астроида.
Точки пересечения эллипса с осями являются его вершинами.
Эксцентриситет эллипса равен отношению 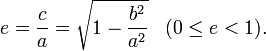 . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут. . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Эллипс также можно описать как
фигуру, которую можно получить из окружности, применяя аффинное преобразование
ортогональную проекцию окружности на плоскость.
Пересечение плоскости и кругового цилиндра
3. Координатное представление 3.1. Эллипс как кривая второго порядка
Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида
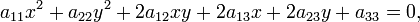
при инвариантах 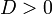 и и 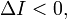 где: где:

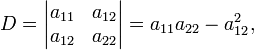
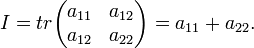
Соотношения между инвариантами кривой второго порядка и полуосями эллипса:


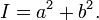
4.2. Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
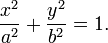
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Для определённости положим, что 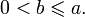 В этом случае величины a и b — соответственно, большая и малая полуоси эллипса. В этом случае величины a и b — соответственно, большая и малая полуоси эллипса.
Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:
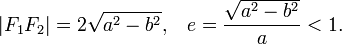
Координаты фокусов эллипса:
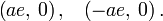
Эллипс имеет две директрисы, уравнения которых можно записать как
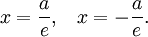
Фокальный параметр (т.е. половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен
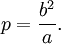
Фокальные радиусы, т. е. расстояния от фокусов до произвольной точки кривой 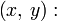

Уравнение диаметра, сопряжённого хордам с угловым коэффициентом k:
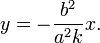
Уравнение касательных, проходящих через точку 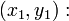
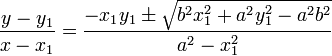
Уравнение касательных, имеющих данный угловой коэффициент k::
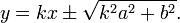
Уравнение нормали в точке 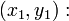
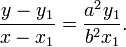
3.3. Параметрическое уравнение
Каноническое уравнение эллипса может быть параметризовано:
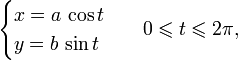
где 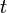 — параметр уравнения. — параметр уравнения.
3.4. Уравнение в полярных координатах
Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах 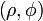 будет иметь вид будет иметь вид
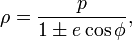
где e — эксцентриситет, а p — фокальный параметр. При положительном знаке перед e второй фокус эллипса будет находиться в точке 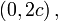 а при отрицательном — в точке а при отрицательном — в точке 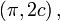 где фокальное расстояние где фокальное расстояние 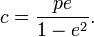
Вывод
Пусть r1 и r2 расстояния до данной точки эллипса из первого и второго фокусов. Пусть, также полюс системы координат находится в первом фокусе, а угол φ отсчитывается от направления на второй полюс. Тогда, из определения эллипса,
r1 + r2 = 2a.
Отсюда,
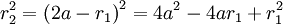 . .
С другой стороны, из теоремы косинусов
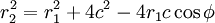 . .
Исключая r2 из последних двух уравнений, получаем
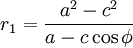
Учитывая, что
p = a(1 − e2),
получаем искомое уравнение.
Другое уравнение в полярных координатах:
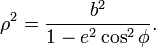
4. Длина дуги эллипса
Длина дуги плоской линии определяется по формуле:
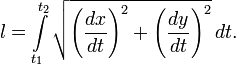
Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:

После замены 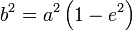 выражение для длины дуги принимает окончательный вид: выражение для длины дуги принимает окончательный вид:
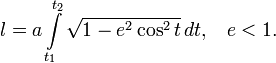
Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода 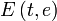 . В частности, периметр эллипса равен: . В частности, периметр эллипса равен:
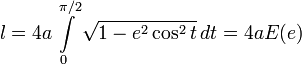 , ,
где 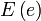 — полный эллиптический интеграл второго рода. — полный эллиптический интеграл второго рода.
4.1. Приближённые формулы для периметра
 . .
Максимальная погрешность этой формулы
0.63% при эксцентриситете эллипса
0.988 (соотношение осей
1/6.5). Погрешность всегда положительная.
Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:
 , где , где 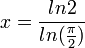 . .
Максимальная погрешность этой формулы
0.36% при эксцентриситете эллипса
0.980 (соотношение осей
1/5). Погрешность также всегда положительная.
Существенно лучшую точность при 0.05 < a / b < 20 обеспечивает формула Рамануджана:
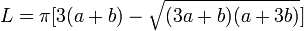 . .
При эксцентриситете эллипса
0.980 (соотношение осей
1/5) погрешность составляет
0.02%. Погрешность всегда отрицательная.
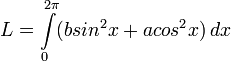 - интеграл от формулы радиуса эллипса. - интеграл от формулы радиуса эллипса.
5. Площадь эллипса и его сегмента
Площадь эллипса вычисляется по формуле
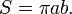
Площадь сегмента между дугой, выпуклой влево, и хордой, проходящей через точки 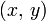 и и 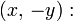

Гипербола
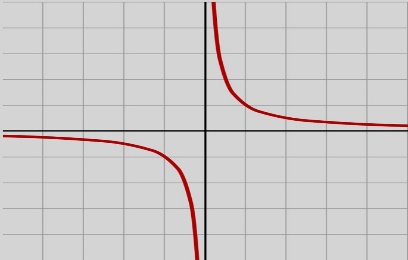
Гипе́рбола (др.-греч. ὑπερβολή, от др.-греч. βαλειν — «бросать», ὑπερ — «сверх») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно. Точнее,
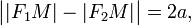 причем | F1F2 | > 2a > 0. причем | F1F2 | > 2a > 0.
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
1. История
Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.
2. Определения
Гипербола может быть определена несколькими путями.
2.1. Коническое сечение
Три основных конических сечения
Гипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как скрещенные и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, скрещенные прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
2.2. Как геометрическое место точек 2.2.1. Через фокусы
Гипербола может быть определена, как Геометрическое место точек, разность расстояний которых до двух заданных точек, называемых фокусами, одинакова и равна 2a.
2.2.2. Через директрису и фокус
Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная ε называется эксцентриситетом гиперболы.
3. Связанные определения
Гипербола состоит из двух отдельных кривых, которые называют ветвями.
Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
Середина большой оси называется центром гиперболы.
Расстояние a от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием с.
Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы.
Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. (Численно прицельный параметр равен b.)
В задачах, связанных с движением тел по гиперболическим траекториям расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием 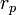 . .
3.1. Соотношения 4. Уравнения
Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
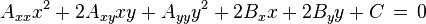 , ,
где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению
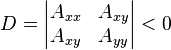
и
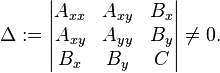
Перемещением центра гиперболы в начало координат и вращением её относительно центра на угол Φ уравнение гиперболы можно привести к каноническому виду
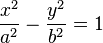 , ,
где большая a и малая b полуоси.
4.2. Полярные координаты
Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то
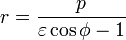
Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то
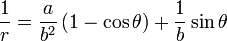
5. Свойства
Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.
Форма гиперболы полностью определяется её эксцентриситетом ε, который для гиперболы всегда больше единицы. Численно, эксцентриситет равен отношению фокального расстояния к большой полуоси. Также эксцентриситет можно определить, как отношение расстояний от произвольной точки гиперболы до фокуса к расстоянию от этой точки до соответствующей прямой, параллельной мнимой оси, называемой директрисой. Отсюда, расстояние от центра гиперболы до директрисы равно a/ε. Эксцентриситет можно выразить с помощью величин a, b, c и θ следующим образом:
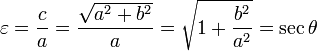
Например, эксцентриситет равнобочной гиперболы, у которой (θ = 45°, a = b) равен
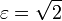 . .
В некоторых прикладных задачах для описания формы гиперболы употребляют коническую константу k, которая связана с эксцентриситетом следующим образом:
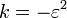 . .
Величина фокального параметра выражается через большую и малую полуоси как
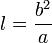 . .
Парабола
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.
1. Уравнения
Каноническое уравнение параболы в прямоугольной системе координат:
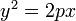 (или (или 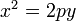 , если поменять местами оси). , если поменять местами оси).
Вывод:
|
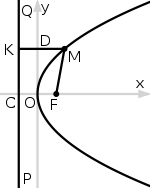
Уравнение директрисы 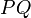 : : 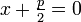 , фокус — , фокус — 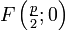 , таким образом начало координат , таким образом начало координат 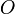 — середина отрезка — середина отрезка 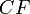 . По определению параболы для любой точки . По определению параболы для любой точки 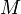 , лежащей на ней выполняется равенство , лежащей на ней выполняется равенство 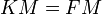 . . 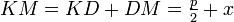 и и 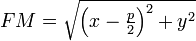 , тогда равенство приобретает вид: , тогда равенство приобретает вид:
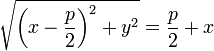 . .
После возведения в квадрат и некоторых преобразований получается равносильное уравнение 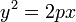 . .
|
Квадратное уравнение 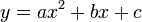 при при  также представляет собой параболу и графически изображается той же параболой, что и также представляет собой параболу и графически изображается той же параболой, что и 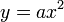 , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке 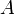 , координаты которой вычисляются по формулам: , координаты которой вычисляются по формулам:
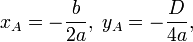 где D = b2 − 4ac - дискриминант где D = b2 − 4ac - дискриминант
Уравнение 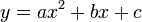 может быть представлено в виде может быть представлено в виде 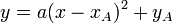 , а в случае переноса начала координат в точку , а в случае переноса начала координат в точку 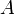 каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим. каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим.
1.1. Расчёт коэффициентов квадратного уравнения
Если для уравнения 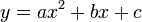 известны координаты 3-х различных точек его графика известны координаты 3-х различных точек его графика 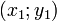 , , 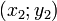 , , 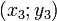 , то его коэффициенты могут быть найдены так: , то его коэффициенты могут быть найдены так:
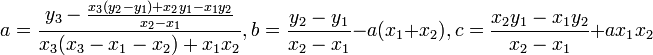
2. Свойства
Парабола — кривая второго порядка.
Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
Для параболы 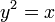 фокус находится в точке (0,25; 0). фокус находится в точке (0,25; 0).
Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
Парабола является антиподерой прямой.
Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
Окружность

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
1. Другие определения
Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.
Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы.
Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.
2. Связанные определения
Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.
Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.
Окружность называется единичной, если ее радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Угол, образуемый дугой окружности, равной по длине радиусу, принимается за 1 радиан.
Длина единичной полуокружности обозначается через π.
Геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое, называется кругом.
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Прямая, проходящая через две различных точки окружности, называется секущей.
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Две окружности, имеющие общий центр, называются концентрическими.
Две окружности, пересекающиеся под прямым углом, называются ортогональными.
3. Свойства
Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на прямой, проходящей через их центры.
Длина дуги окружности радиуса R, образованной центральным углом  , измеренным в радианах, можно вычислить по формуле , измеренным в радианах, можно вычислить по формуле 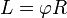 . .
Длину окружности с радиусом R можно вычислить по формуле 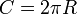 . .
Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.
Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.
Угол между двумя секущими, проведёнными из точки, лежащей вне окружности равен полуразности мер дуг, лежащих между секущими.
Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле и дуги напротив нее.
Угол между касательной и хордой равен половине градусной меры дуги, стягиваемой хордой.
Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
При пересечении двух хорд произведение отрезков, на которые делится одна из них точкой пересечения, равно произведению отрезков другой.
Произведение длин расстояний от выбранной точки до двух точек пересечения окружности и секущей, проходящей через выбранную точку, не зависит от выбора секущей и равно абсолютной величине степени точки относительно окружности.
Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равен абсолютной величине степени точки относительно окружности.
Окружность является простой плоской кривой второго порядка.
Окружность является коническим сечением и частным случаем эллипса.
4. Основные формулы
Длина окружности: L = 2πR = πD
Радиус окружности: R = L/2π
Диаметр окружности: D = L/π
5. Уравнения 5.1. Декартовы координаты
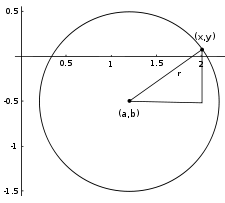
Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)
Общее уравнение окружности записывается как:
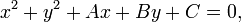
или
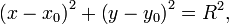
где
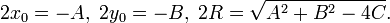
Точка 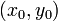 — центр окружности, R — её радиус. — центр окружности, R — её радиус.
Уравнение окружности радиуса R с центром в начале координат:
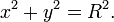
Уравнение окружности, проходящей через три точки (с помощью определителя) 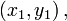 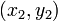 и и 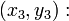
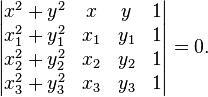
Окружность также можно описать с помощью параметрического уравнения:
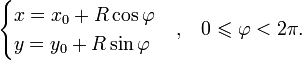
В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:
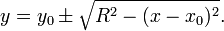
Если центр окружности совпадает с началом координат, функции принимают вид:
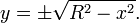
5.2. Полярные координаты
Окружность радиуса R с центром в точке 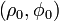 : :
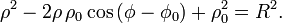
Если полярные координаты центра окружности 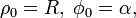 то проходящая через начало координат окружность описывается уравнением: то проходящая через начало координат окружность описывается уравнением:
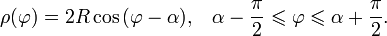
Если же центр является началом координат, то уравнение будет иметь вид:
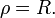
5.3. Комплексная плоскость
На комплексной плоскости окружность задаётся формулой:
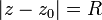
или в параметрическом виде
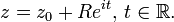
6. Касательные и нормали
Уравнение касательной к окружности в точке 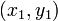 определяется уравнением определяется уравнением
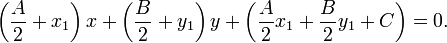
Уравнение нормали в той же точке можно записать как
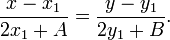
7. Концентрические и ортогональные окружности
Две окружности, заданные уравнениями:
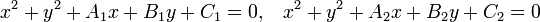
являются концентрическими (то есть имеющими общий центр) в том и только в том случае, когда A1 = A2 и B1 = B2.
Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие
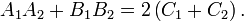 |
 Скачать 249.22 Kb.
Скачать 249.22 Kb.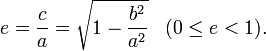 . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
. Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
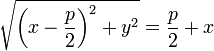 .
.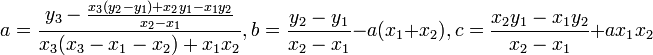


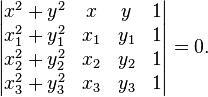
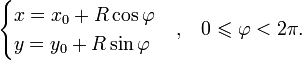



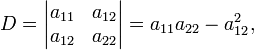
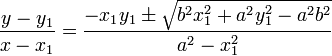
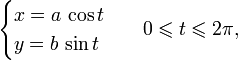
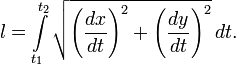

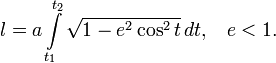
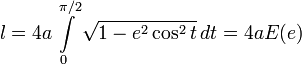 ,
, - интеграл от формулы радиуса эллипса.
- интеграл от формулы радиуса эллипса.