|
|
Пространство геометрических векторов
Лекция 1
Глава 1
Пространство геометрических векторов
Линейные операции над геометрическими векторами. Коллинеарные и компланарные векторы. Базис, координаты вектора, их свойства. Проекция вектора на ось. Декартов базис и декартовы координаты вектора. Декартовы координаты точки.
|
1.1. Понятие геометрического вектора.
Линейные операции над векторами, их свойства
Определение 1. Геометрическим вектором (или просто вектором) называется отрезок, концы которого рассматриваются в определенном порядке (т. е. указано, какая из его граничных точек является началом, а какая - концом).
Е сли за начало отрезка сли за начало отрезка 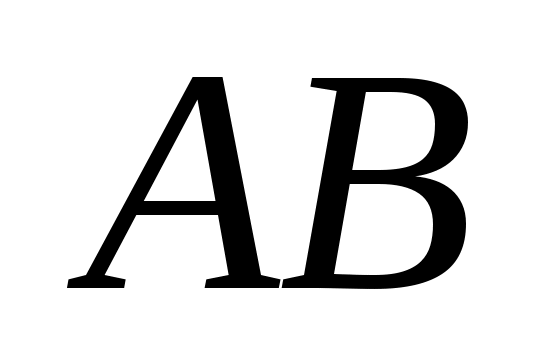 принята точка принята точка  , вектор будем обозначать символом , вектор будем обозначать символом 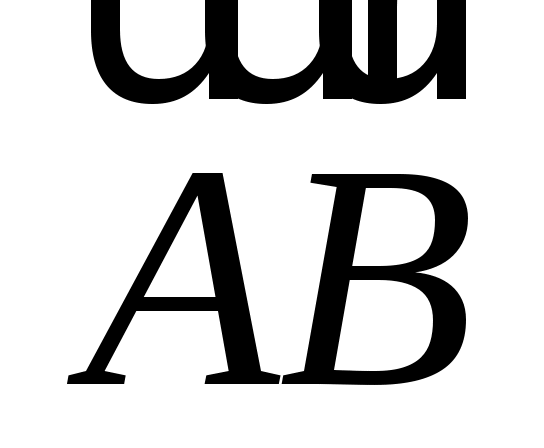 (либо одной малой латинской буквой, например, (либо одной малой латинской буквой, например,  ), а точку ), а точку  называть точкой приложения вектора. называть точкой приложения вектора.
На чертеже вектор 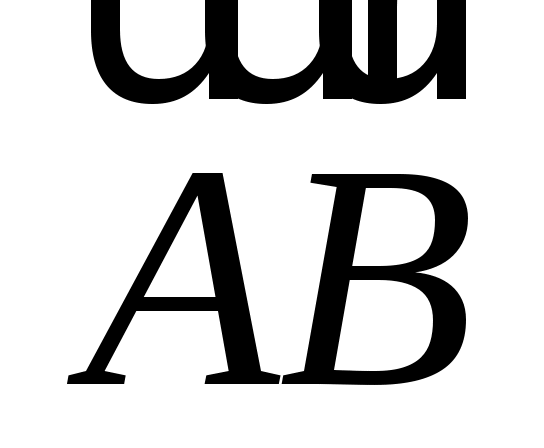 будем изображать отрезком со стрелкой в конечной точке (рис. 1.1). будем изображать отрезком со стрелкой в конечной точке (рис. 1.1).
Длиной вектора 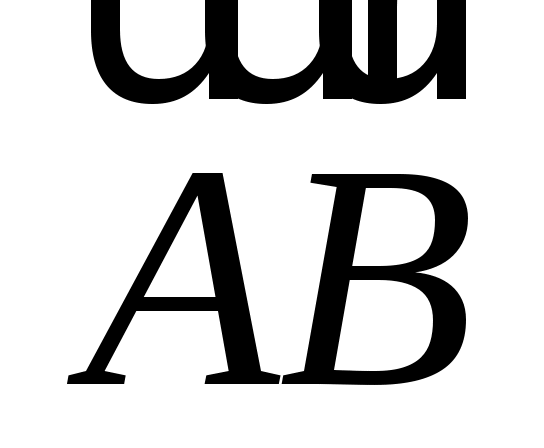 назовем длину отрезка назовем длину отрезка 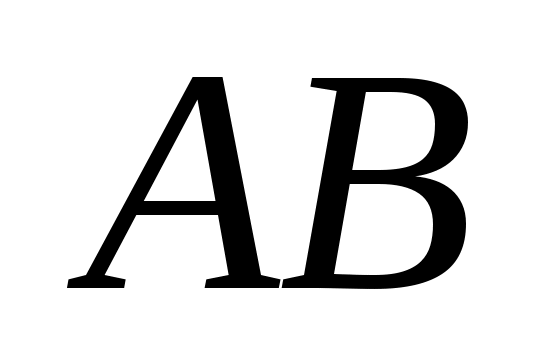 и в записи используем знак абсолютной величины: и в записи используем знак абсолютной величины:  (либо (либо  ). ).
Вектор 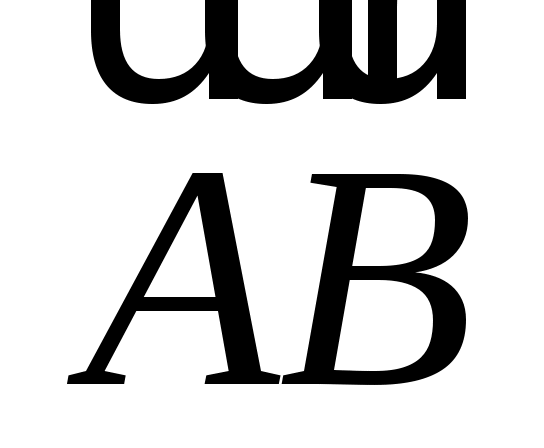 называется нулевым вектором, если его конечная точка называется нулевым вектором, если его конечная точка 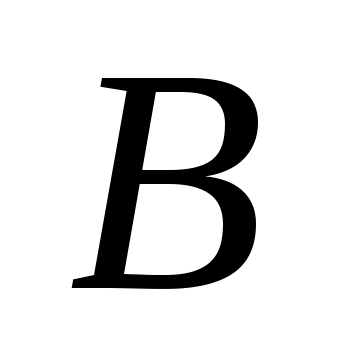 совпадает с начальной совпадает с начальной  . .
Нулевой вектор в силу его определения не имеет направления, а длина его равна нулю.
Векторы 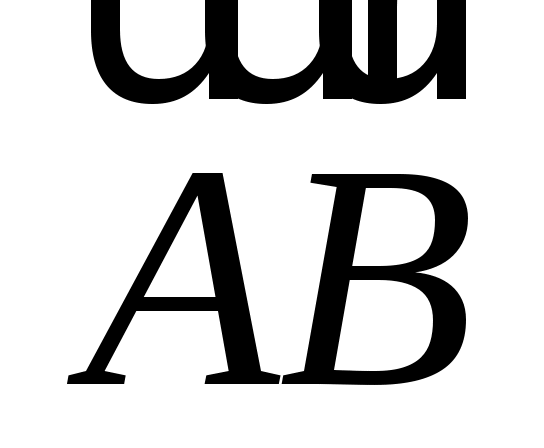 и и 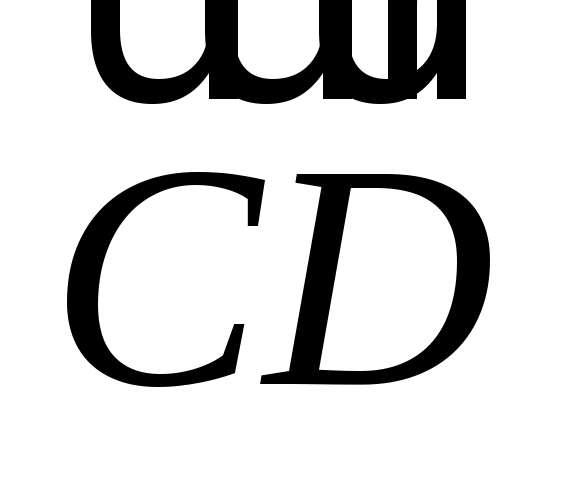 назовем коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 1.2; 1.3). назовем коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 1.2; 1.3).
Два вектора 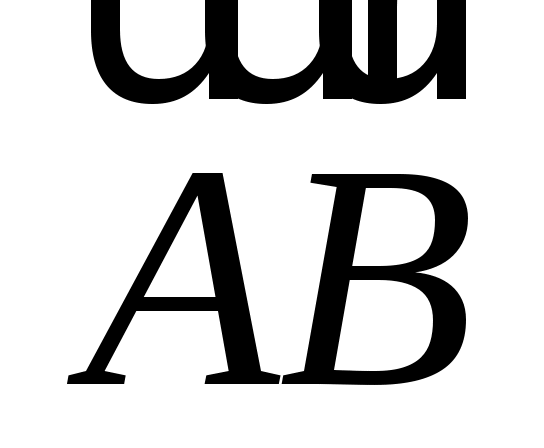 и и 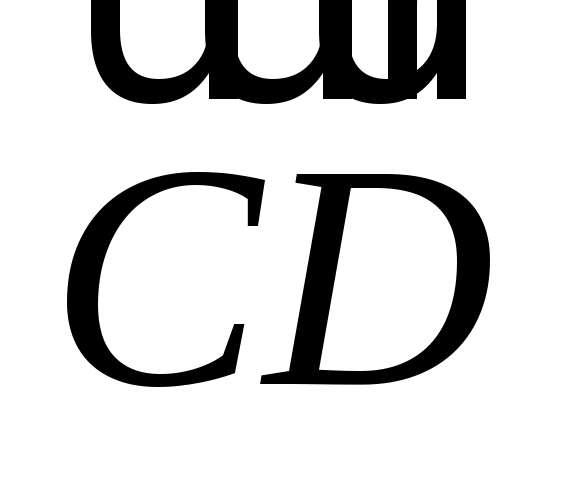 называют равными, если они коллинеарны, имеют общее направление и равные длины (рис. 1.4). называют равными, если они коллинеарны, имеют общее направление и равные длины (рис. 1.4).

Из определения следует, что два вектора, порознь равные третьему, равны между собой. Именно поэтому в аналитической геометрии не различают равные векторы, имеющие разные точки приложения. Векторы, изучаемые в аналитической геометрии, называются свободными.
О пределение 2. Суммой векторов пределение 2. Суммой векторов 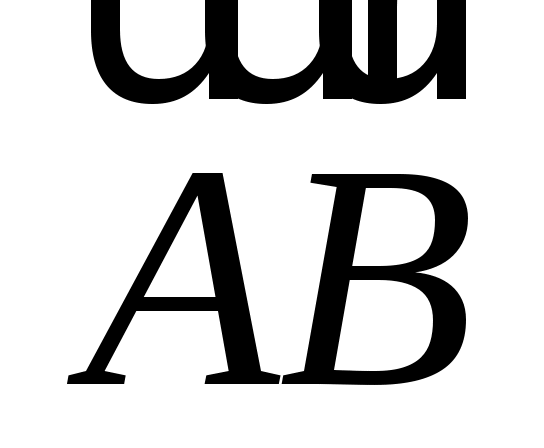 и и 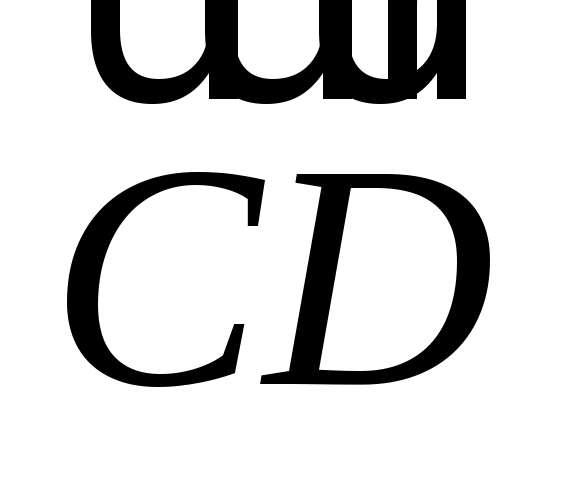 называется вектор, идущий из начала первого вектора ( называется вектор, идущий из начала первого вектора (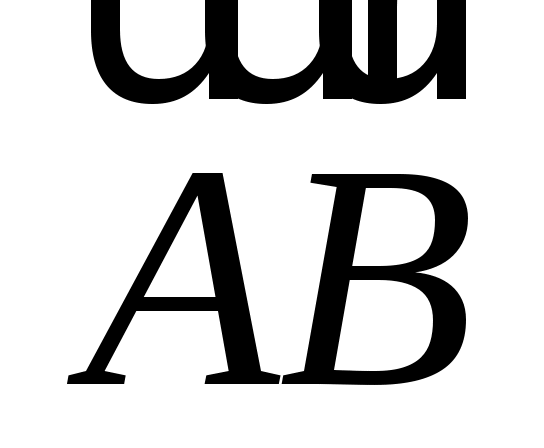 ) в конец второго ( ) в конец второго (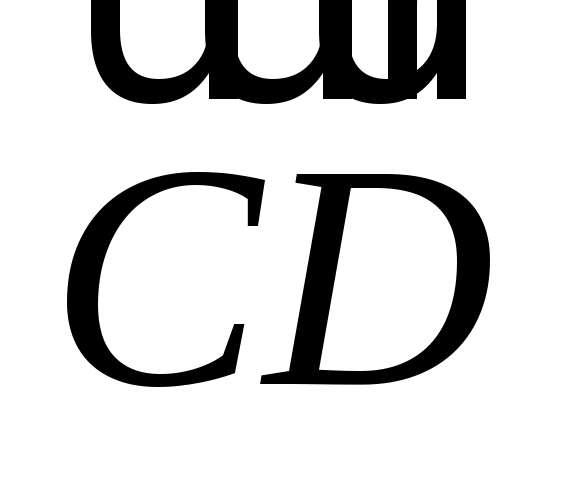 ), при условии, что ), при условии, что 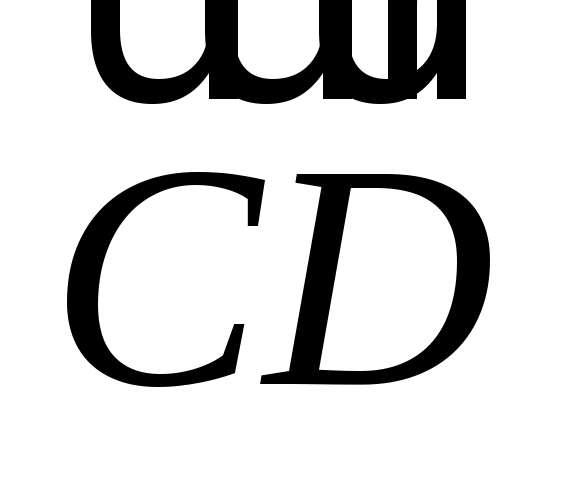 приложен к концу вектора приложен к концу вектора 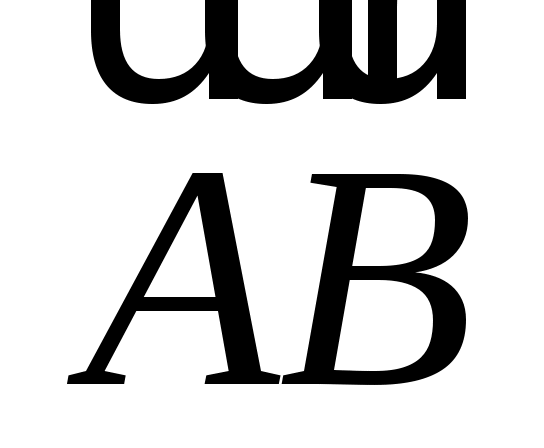 (рис. 1.5). (рис. 1.5).
Обозначать сумму в тексте будем 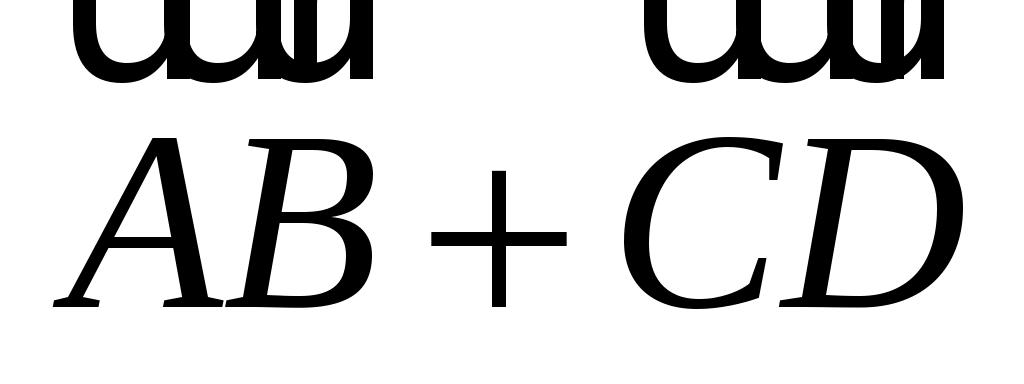 (либо (либо 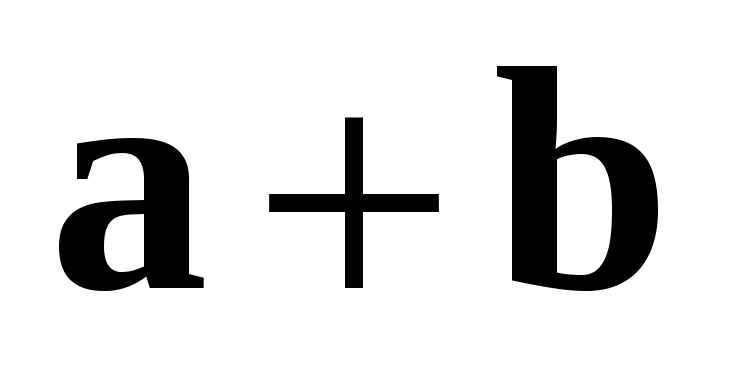 , если , если 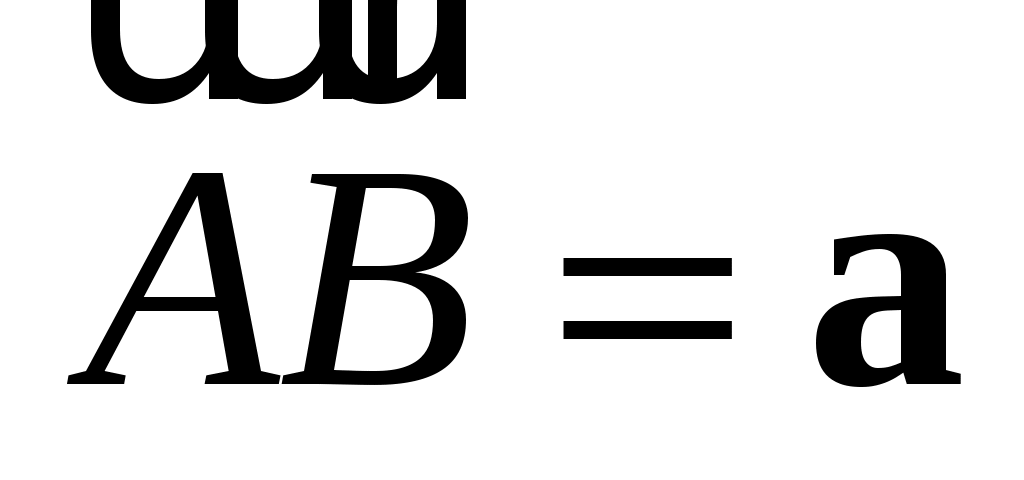 , ,  ). ).
Замечание 1. Из определения 2 следует так называемое «правило параллелограмма»: если векторы  и и  приложены к одной точке (одному началу), то сумма приложены к одной точке (одному началу), то сумма 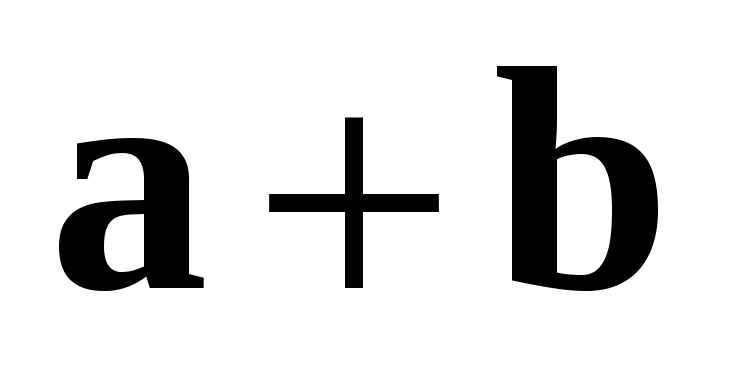 представляет собой диагональ параллелограмма, построенного на векторах представляет собой диагональ параллелограмма, построенного на векторах  и и  как на сторонах. как на сторонах.
Д ействительно, в параллелограмме ействительно, в параллелограмме  (рис. 1.6) векторы (рис. 1.6) векторы 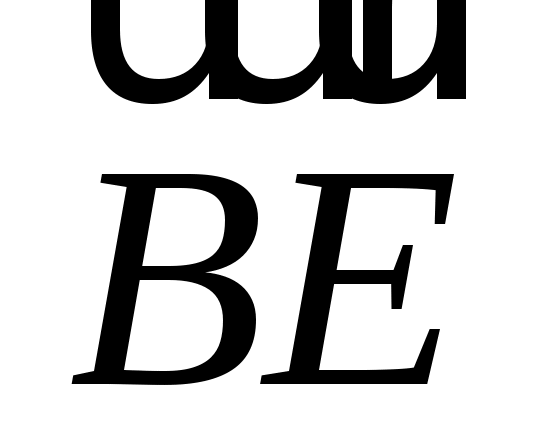 и и  равны: равны: 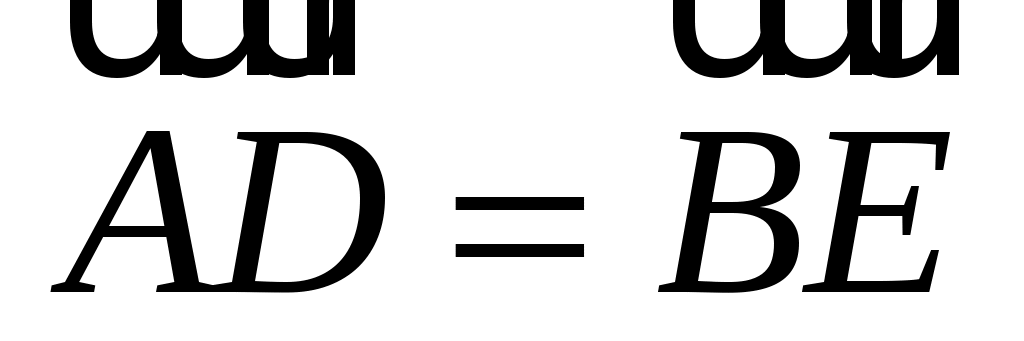 , а тогда по определению 2 диагональ , а тогда по определению 2 диагональ  или или  . .
Докажем два свойства операции сложения геометрических векторов:
1) для любых двух геометрических векторов  и и  : :
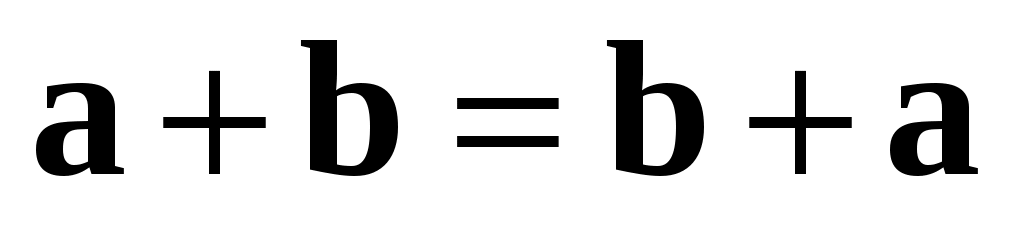 ; ;
2) для любых трех геометрических векторов  , ,  и и  : :
 . .
Д оказательство свойства 1. оказательство свойства 1.
Приложим векторы  и и  к одному началу – произвольной точке к одному началу – произвольной точке 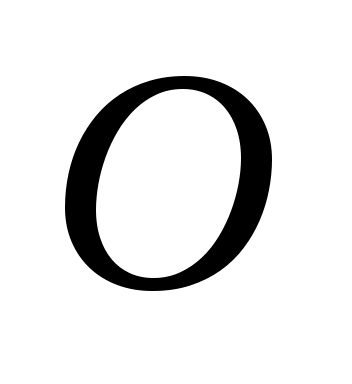 , концевые точки обозначим так, как показано на рис. 1.7 и рассмотрим треугольники , концевые точки обозначим так, как показано на рис. 1.7 и рассмотрим треугольники  и и 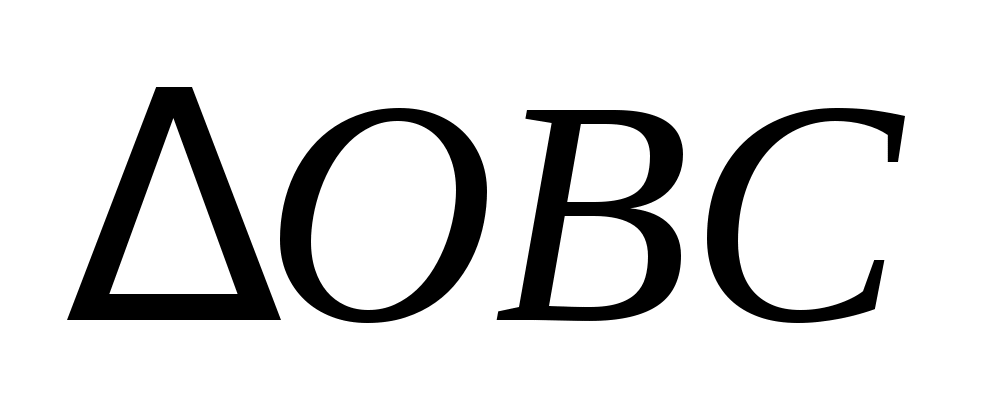 . .
Из  вектор вектор 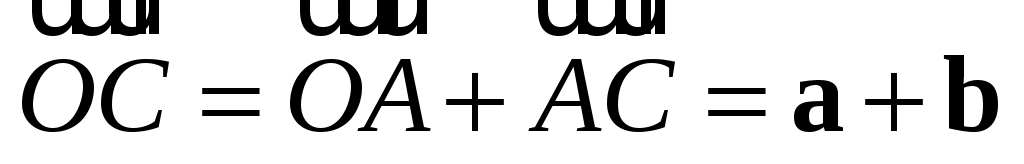 , так как по определению равных векторов , так как по определению равных векторов 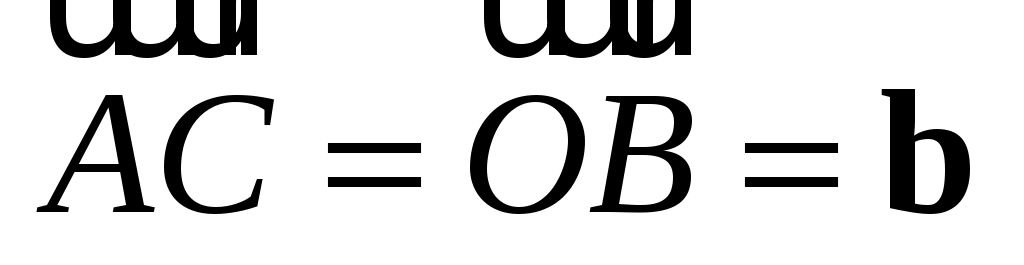 . .
С другой стороны, из 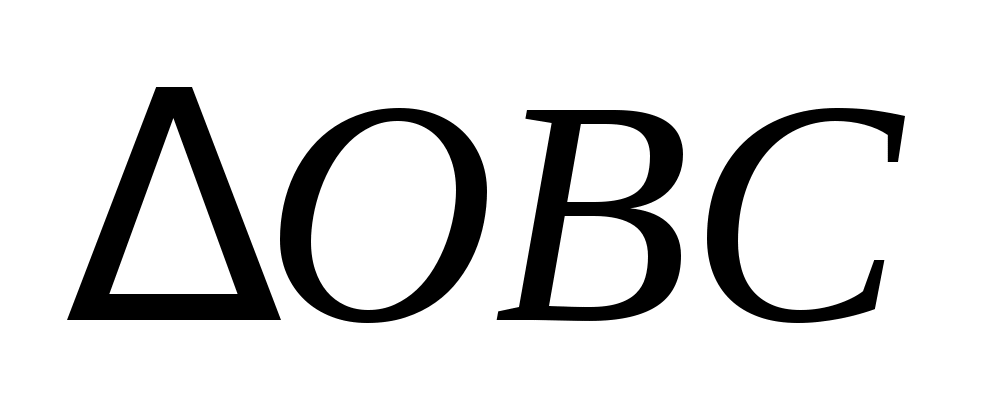 тот же самый вектор тот же самый вектор 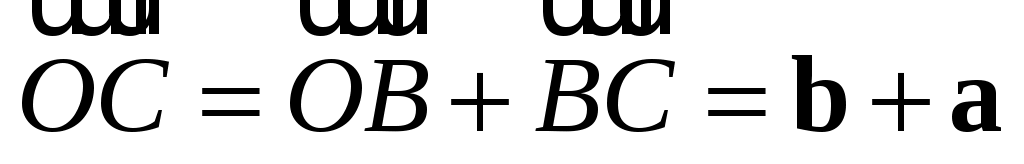 , так как , так как 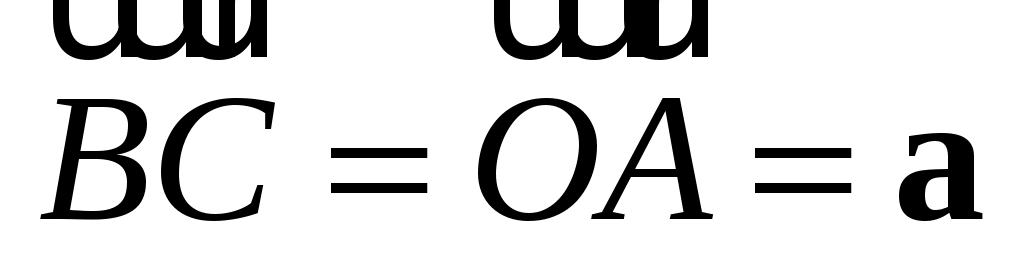 . .
Таким образом, 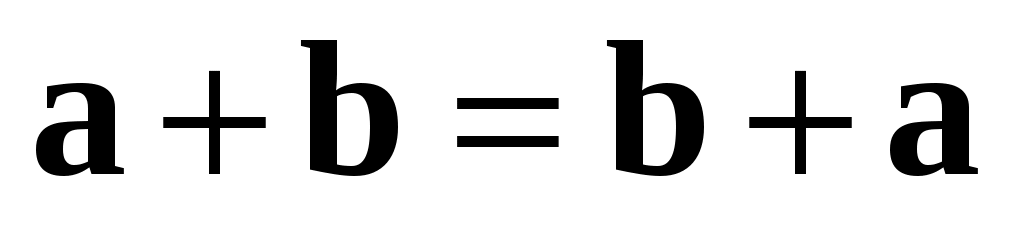 , и свойство 1 доказано. , и свойство 1 доказано.
Доказательство свойства 2.
П риложим вектор риложим вектор  к произвольной точке к произвольной точке 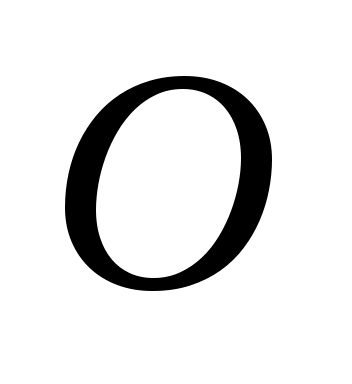 , к концу вектора , к концу вектора  приложим вектор приложим вектор  , к концу , к концу  - вектор - вектор  . Концевые точки обозначим так, как показано на рис. 1.8, и рассмотрим вектор . Концевые точки обозначим так, как показано на рис. 1.8, и рассмотрим вектор 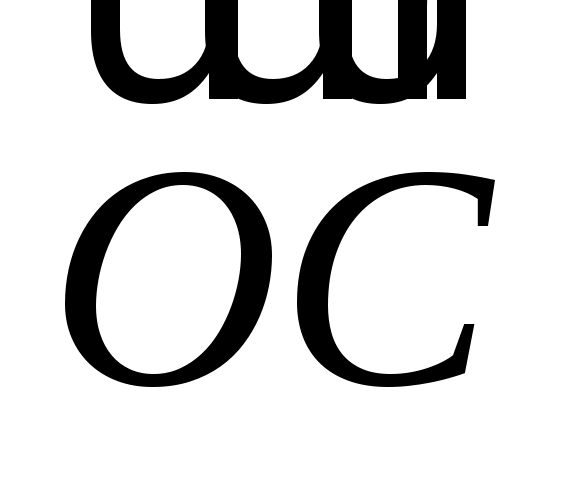 , идущий из начала , идущий из начала  в конец вектора в конец вектора  . .
Из  имеем: имеем:
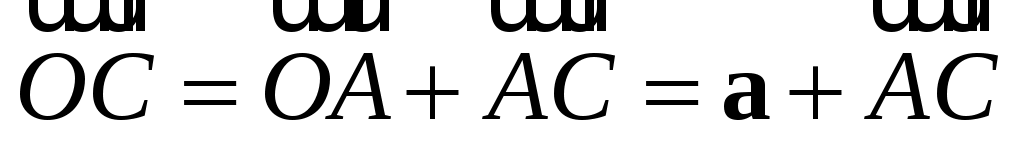 , (1.1) , (1.1)
но вектор  из из 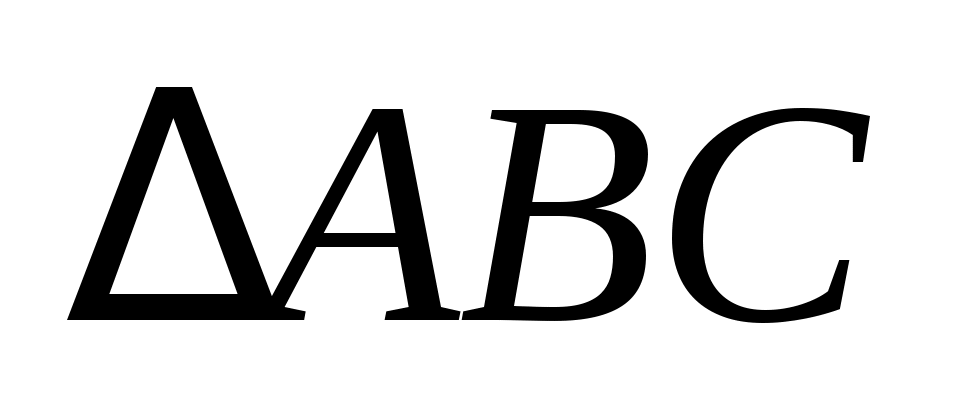 равен равен
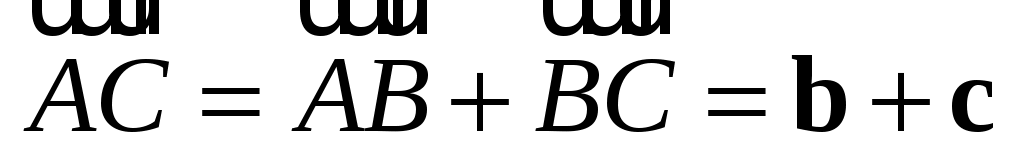 . (1.2) . (1.2)
Из (1.1) и (1.2) получим
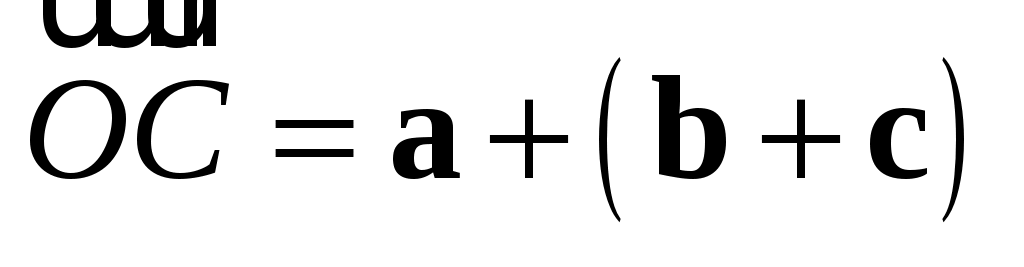 . (1.3) . (1.3)
С другой стороны, тот же самый вектор 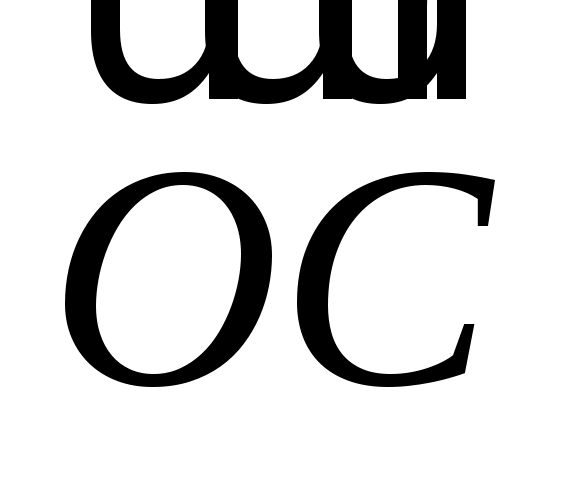 из треугольника из треугольника 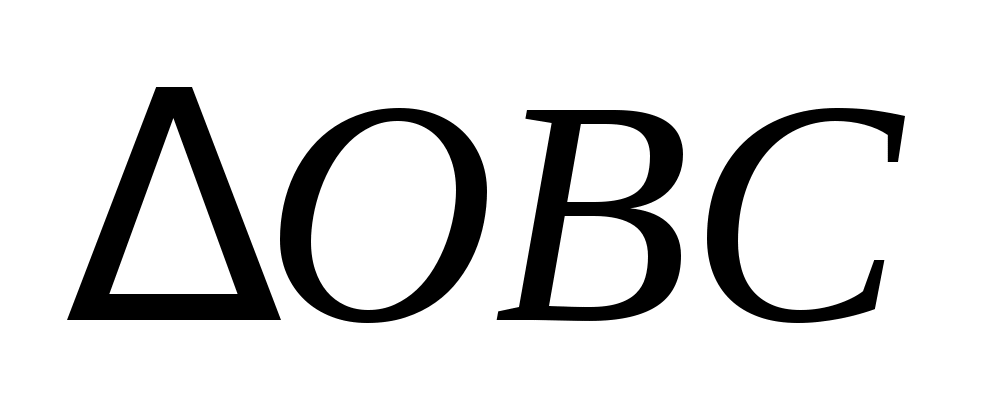 можно записать в виде можно записать в виде
 , (1.4) , (1.4)
но из 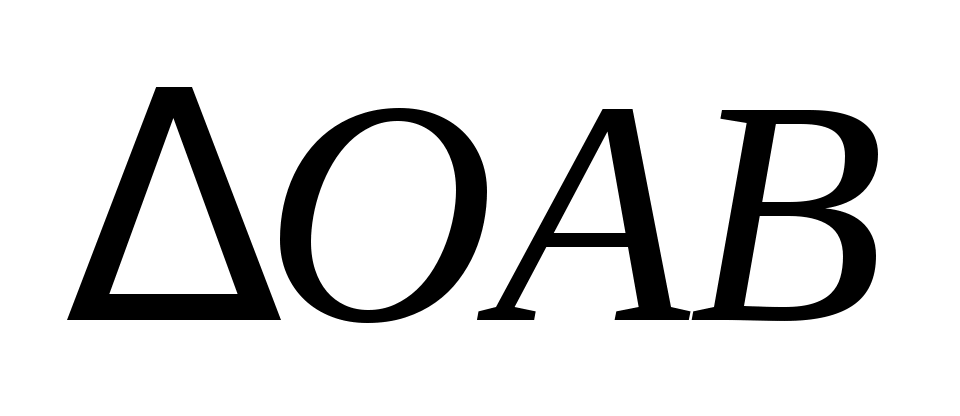
 . (1.5) . (1.5)
Равенства (1.4) и (1.5) дают следующее:
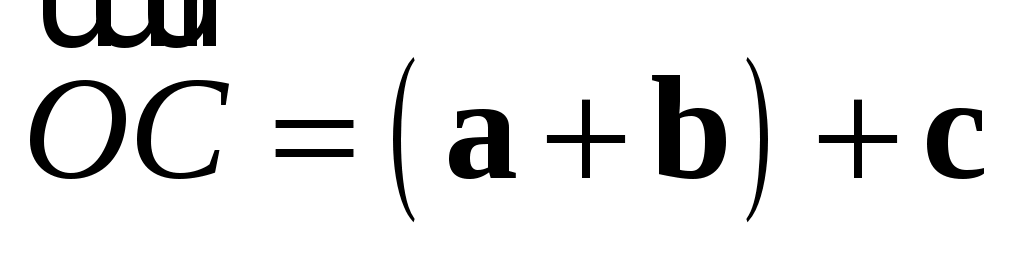 . .
Сравнив последнее равенство с (1.3), получим
 , ,
и свойство 2 доказано.
Замечание 2. Свойство 2 означает, что мы можем далее не различать векторы 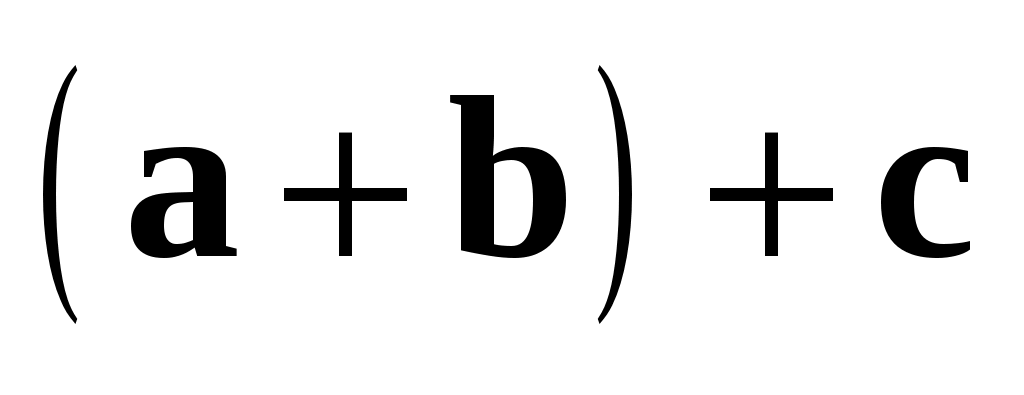 и и 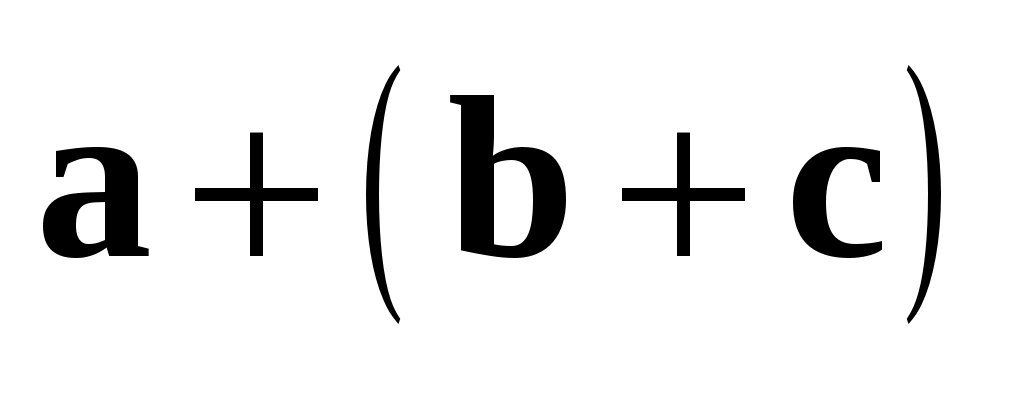 , а рассматривать их как один и тот же вектор , а рассматривать их как один и тот же вектор 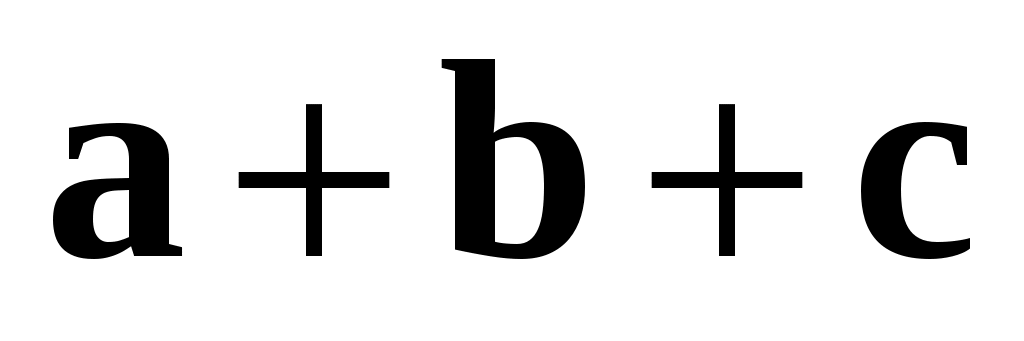 . .
С умма произвольного числа векторов умма произвольного числа векторов 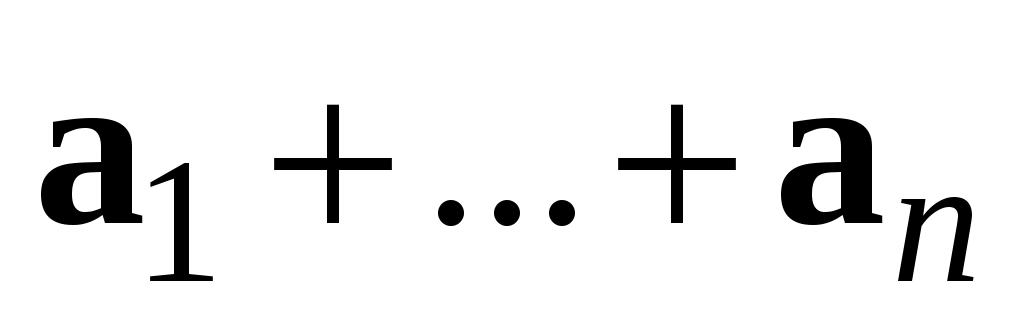 может быть получена по следующему правилу: к произвольной точке может быть получена по следующему правилу: к произвольной точке 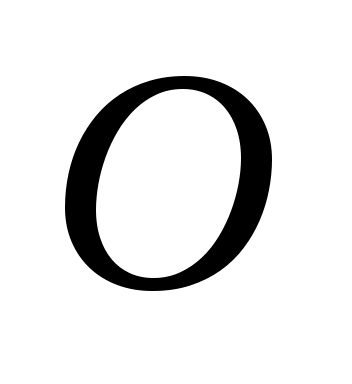 приложим вектор приложим вектор  , к его концу – вектор , к его концу – вектор 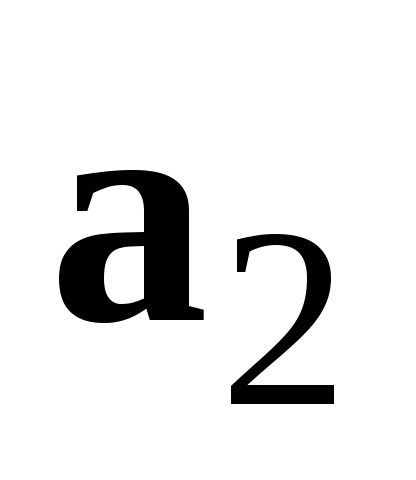 и так далее, к концу вектора и так далее, к концу вектора 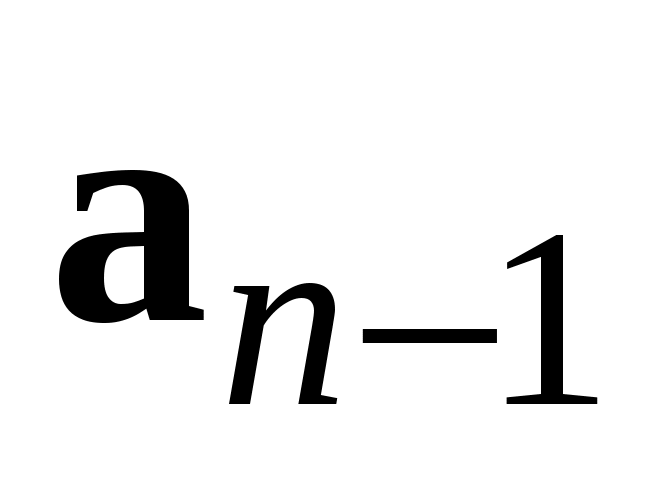 приложим вектор приложим вектор 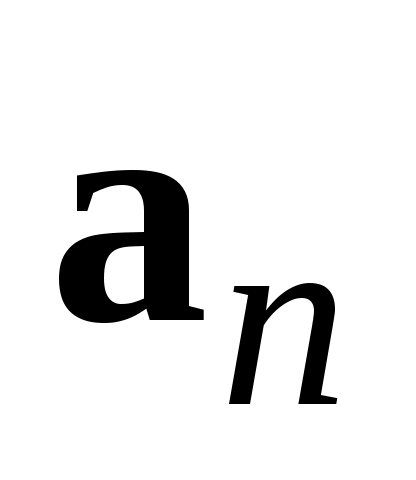 , тогда вектор, начало которого совпадет с началом , тогда вектор, начало которого совпадет с началом  , а конец – с концом , а конец – с концом 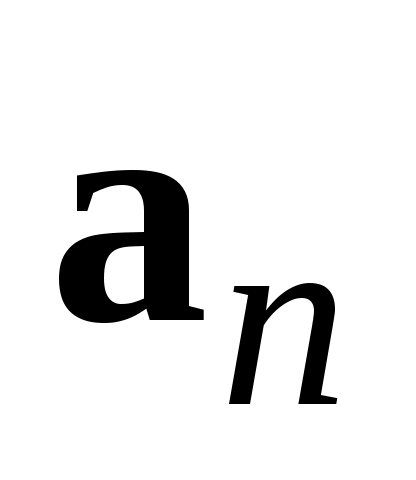 , и будет вектором , и будет вектором 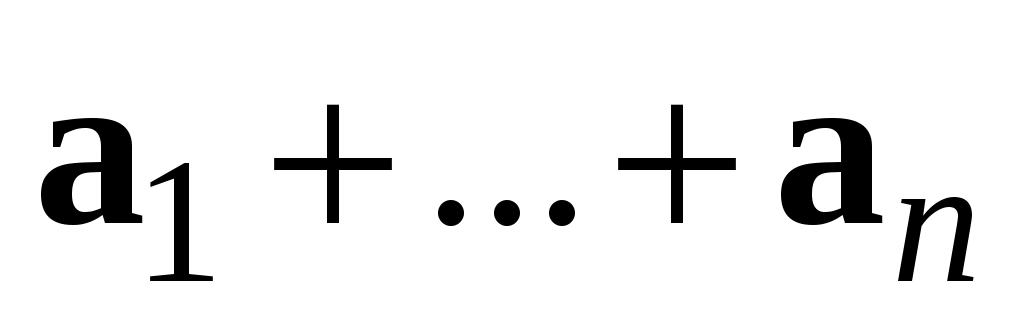 (рис. 1.9). (рис. 1.9).
Замечание 3. Существует такой вектор 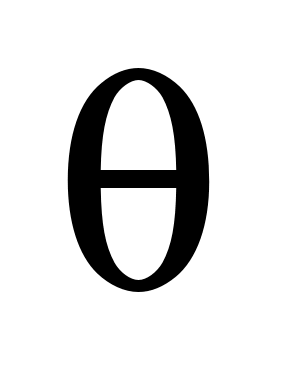 , что для любого геометрического вектора , что для любого геометрического вектора  справедливо равенство справедливо равенство
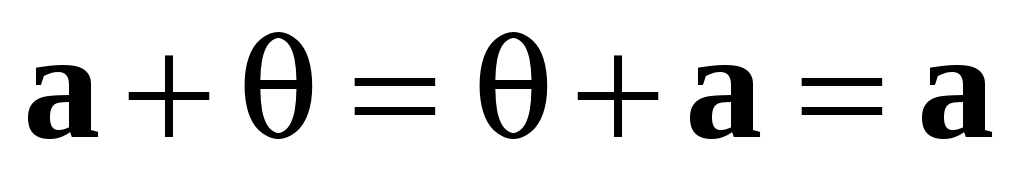 . .
Действительно, в качестве вектора 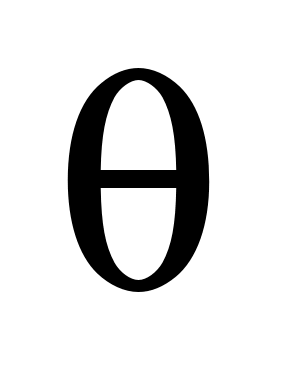 можно взять введенный ранее нулевой вектор. можно взять введенный ранее нулевой вектор.
Если  – произвольный геометрический вектор, то по определению суммы вектор – произвольный геометрический вектор, то по определению суммы вектор  имеет начало в начале имеет начало в начале  , а конец – в конце второго слагаемого, т. е. , а конец – в конце второго слагаемого, т. е. 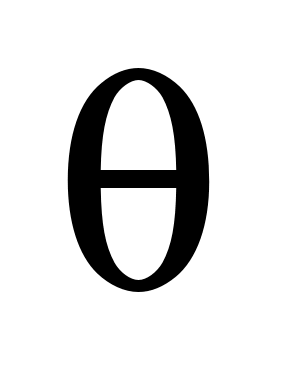 , но у , но у 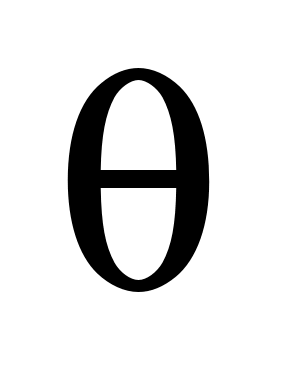 начало и конец совпадают и, таким образом, у вектора начало и конец совпадают и, таким образом, у вектора  начало совпадает с началом вектора начало совпадает с началом вектора  , а конец – с концом вектора , а конец – с концом вектора  и и 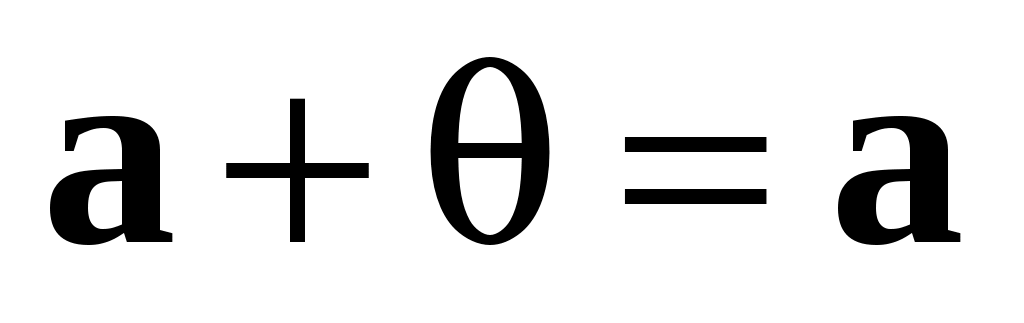 . .
Аналогично устанавливаем, что 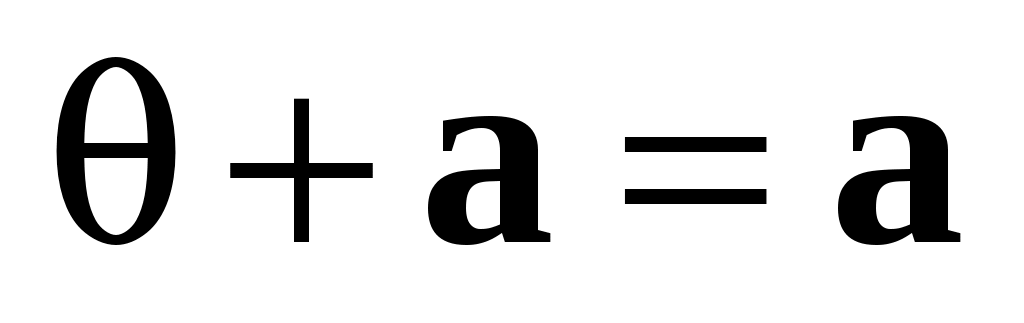 . .
Определение 3. Разностью векторов  и и  называется такой вектор называется такой вектор  , что , что  . .
Запись:  . .
И з определения 3 следует, что если привести векторы з определения 3 следует, что если привести векторы  и и  к одному началу, то к одному началу, то  изображается вектором, идущим из конца изображается вектором, идущим из конца  в конец в конец  (рис. 1.10). (рис. 1.10).
Определение 4. Произведением вектора  на число на число 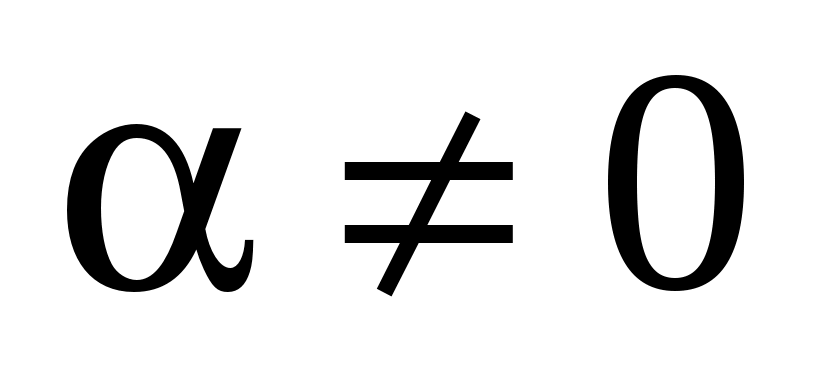 назовем вектор назовем вектор  , удовлетворяющий следующим трем условиям: , удовлетворяющий следующим трем условиям:
 коллинеарен коллинеарен  ; ;
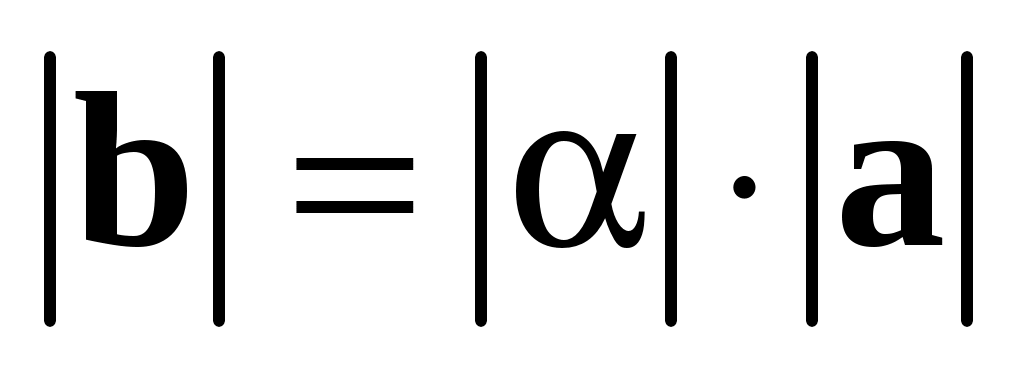 ; ;
направление  совпадает с направлением совпадает с направлением  , если , если 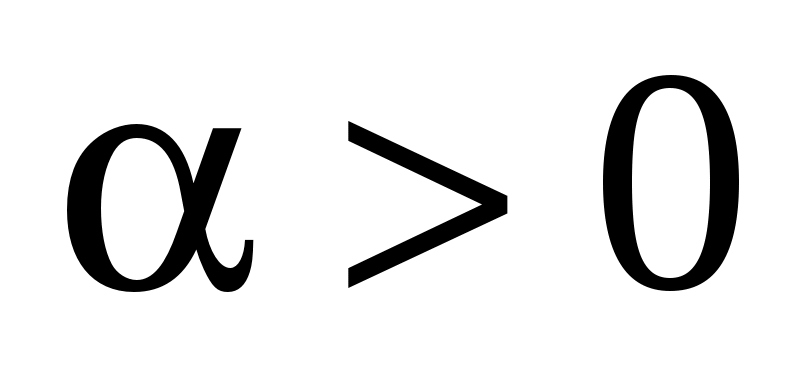 , и противоположно ему, если , и противоположно ему, если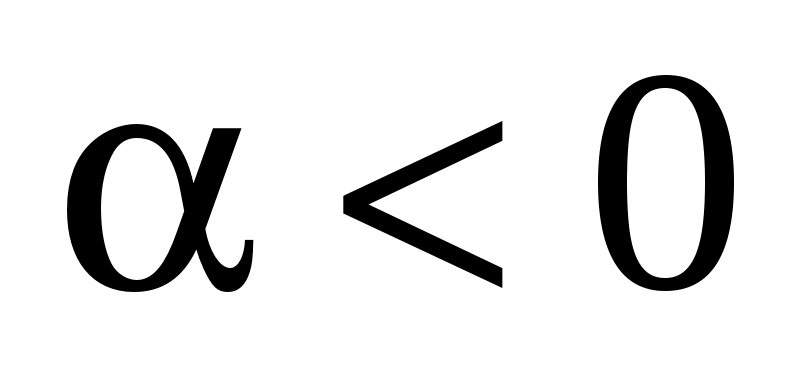 . .
Под произведением вектора  на на  будем понимать нулевой вектор будем понимать нулевой вектор 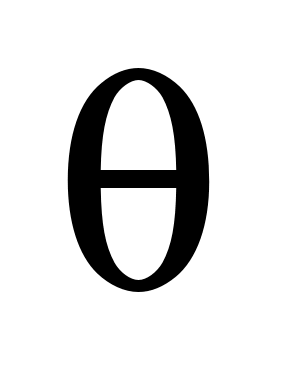 . .
Запись: 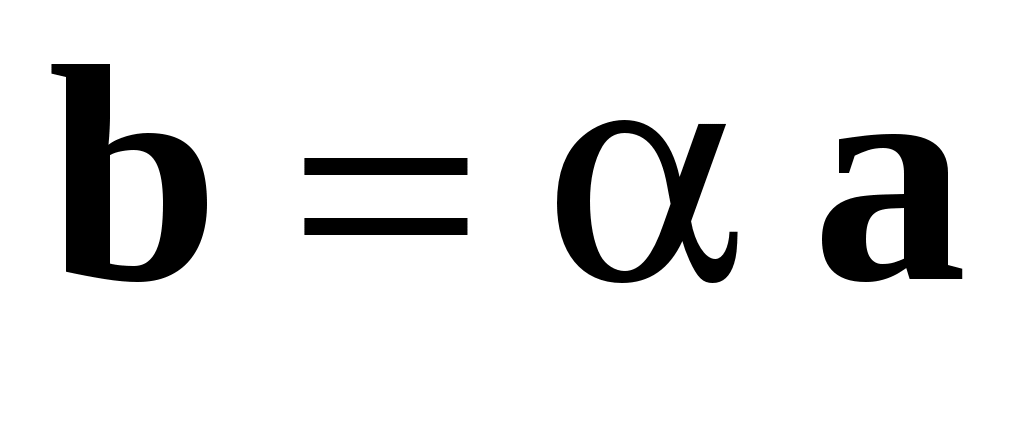 . .
З амечание 4. Вектор амечание 4. Вектор 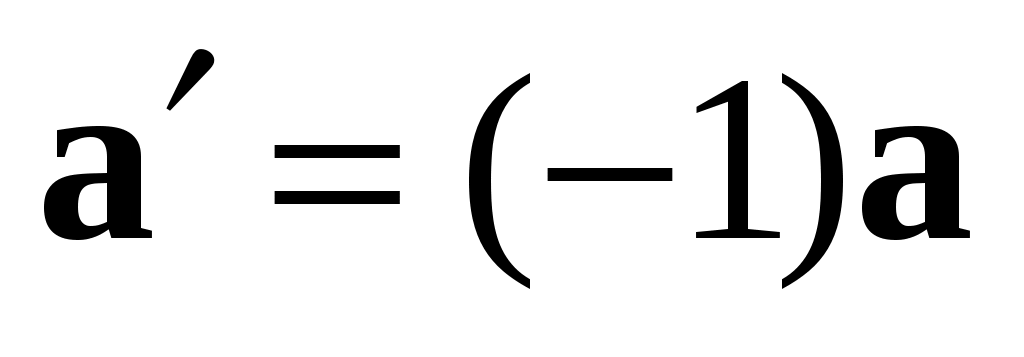 имеет длину такую же, как вектор имеет длину такую же, как вектор  ( (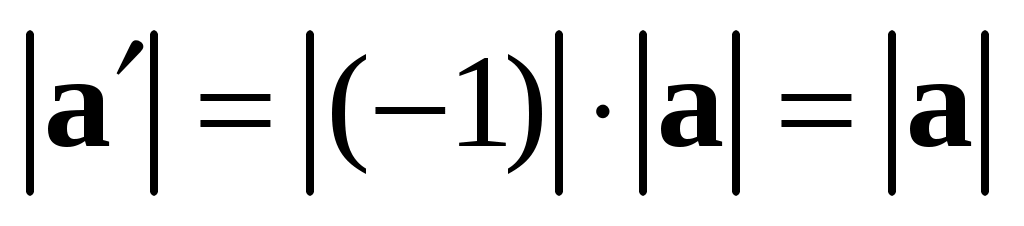 ), и направление, противоположное направлению ), и направление, противоположное направлению  (так как число (так как число 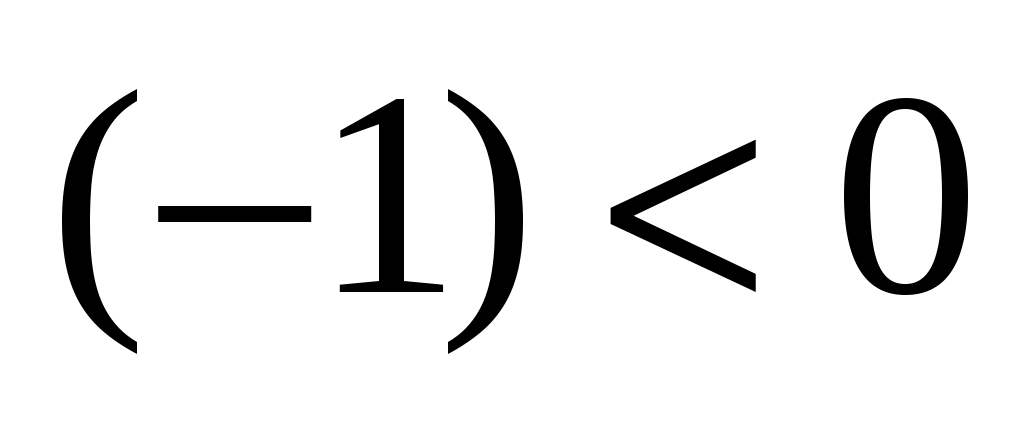 ). ).
Вектор  называется противоположным для вектора называется противоположным для вектора  (рис. 1.11). (рис. 1.11).
Замечание 5. Для любых векторов  и и  , если , если  , ,  , равенство , равенство 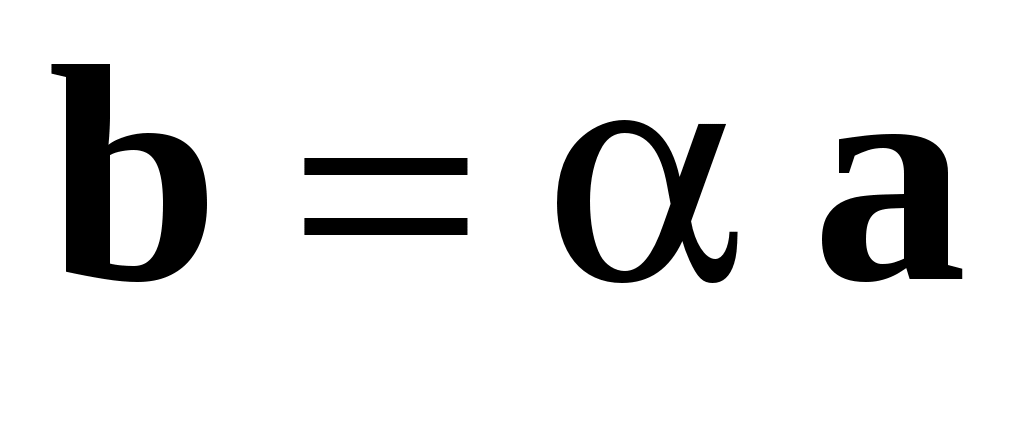 есть необходимое и достаточное условие коллинеарности векторов есть необходимое и достаточное условие коллинеарности векторов  и и  . .
В самом деле, пусть  , ,  и и 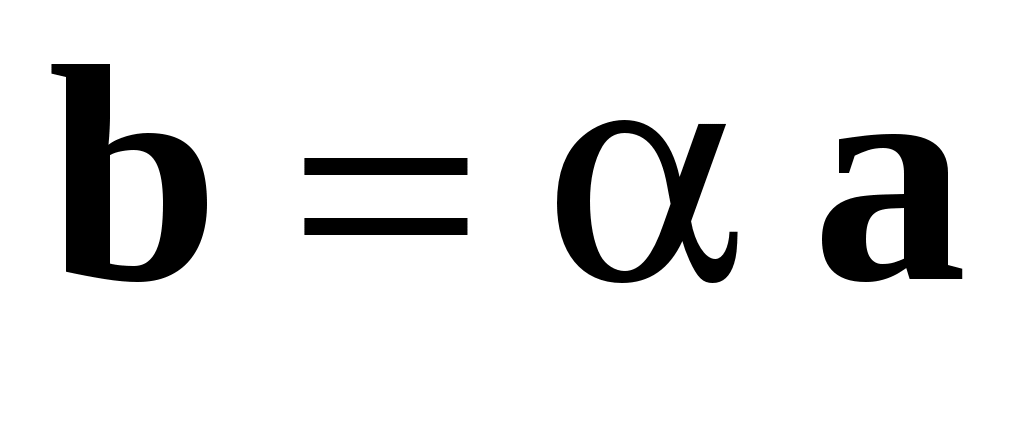 . Тогда в соответствии с определением 4 . Тогда в соответствии с определением 4  и и  коллинеарны. коллинеарны.
Обратно. Пусть  и и  коллинеарны. Так как коллинеарны. Так как  , ,  , можно рассмотреть векторы , можно рассмотреть векторы 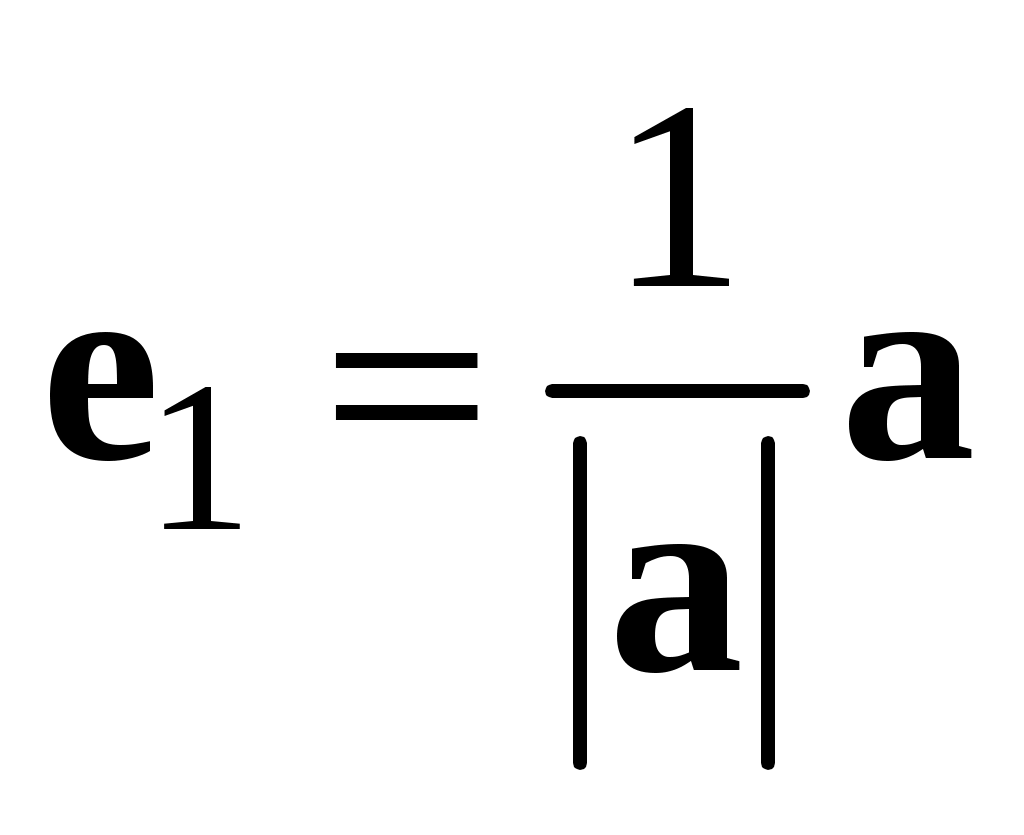 и и 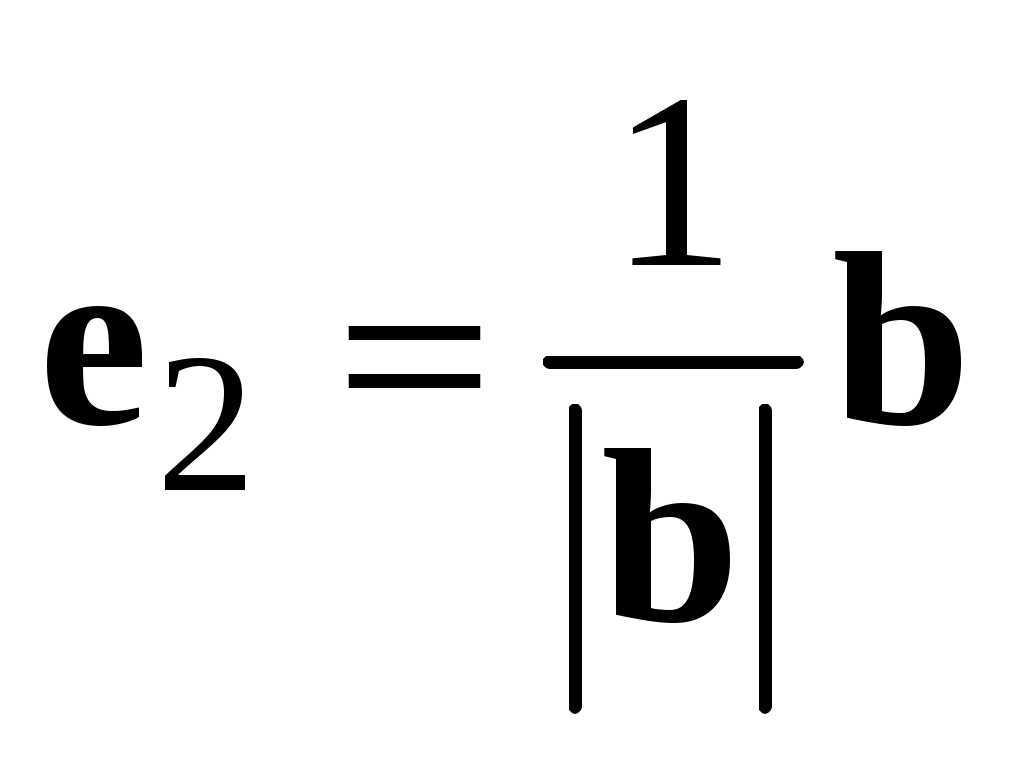 . .
В соответствии с определением 4 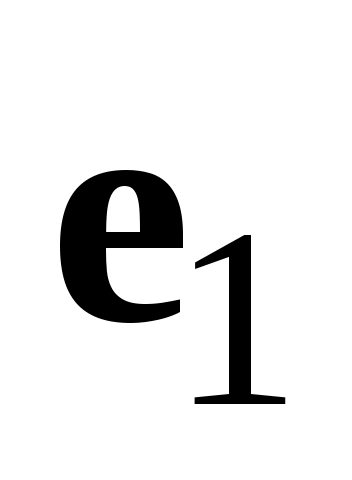 и и  коллинеарны, аналогично коллинеарны, аналогично 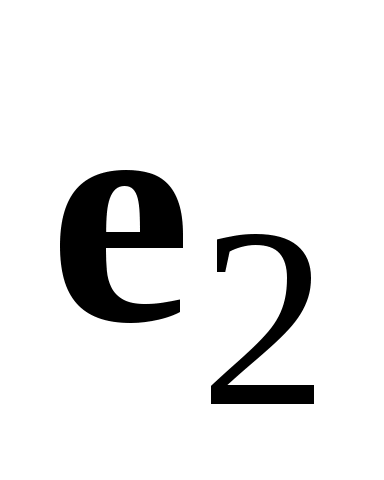 и и  коллинеарны, но тогда коллинеарны, но тогда 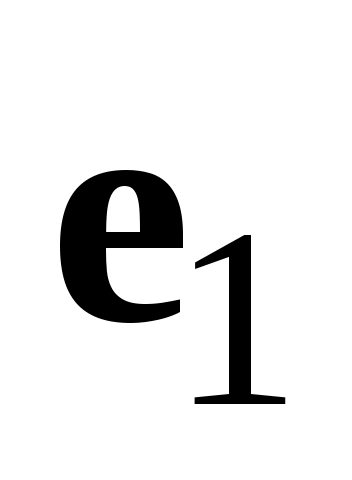 и и 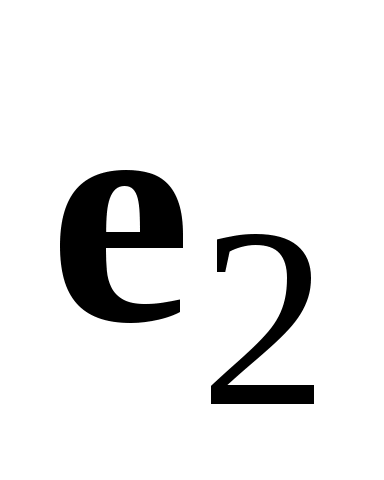 тоже коллинеарны. тоже коллинеарны.
Имеем  и и 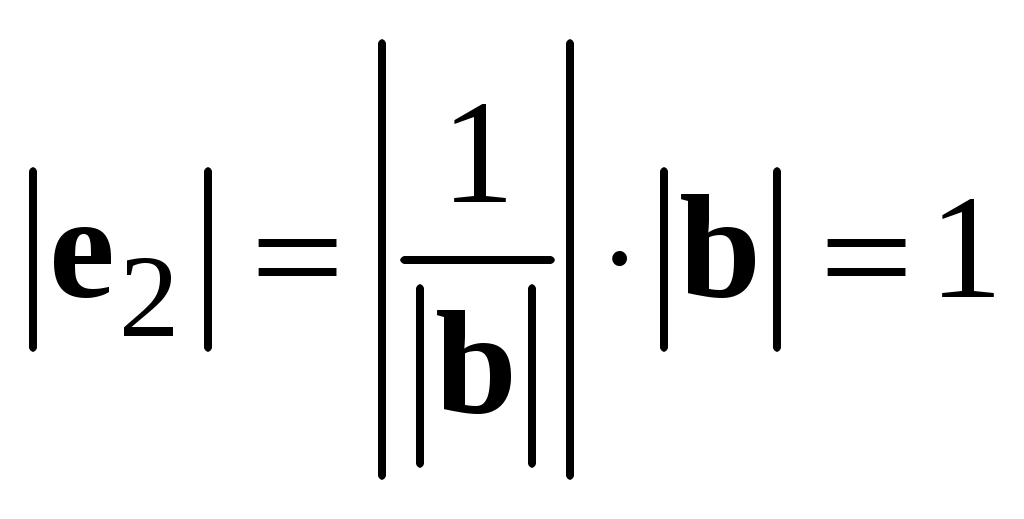 . .
Таким образом, 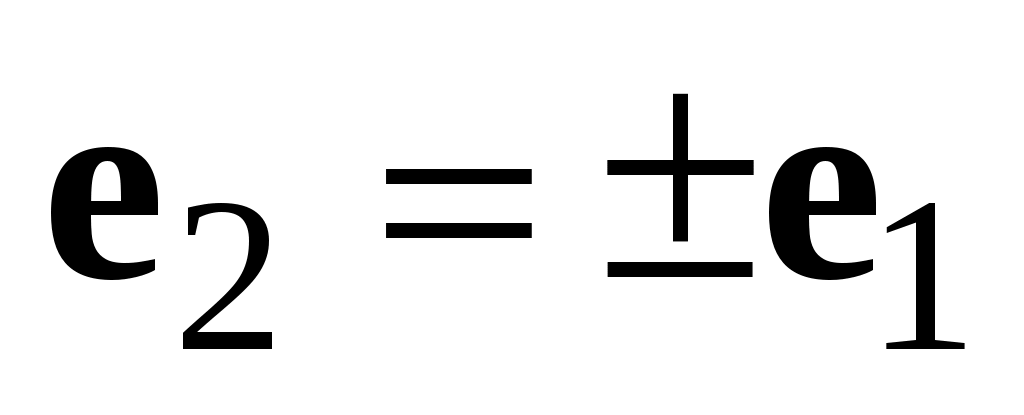 , т.е. , т.е. 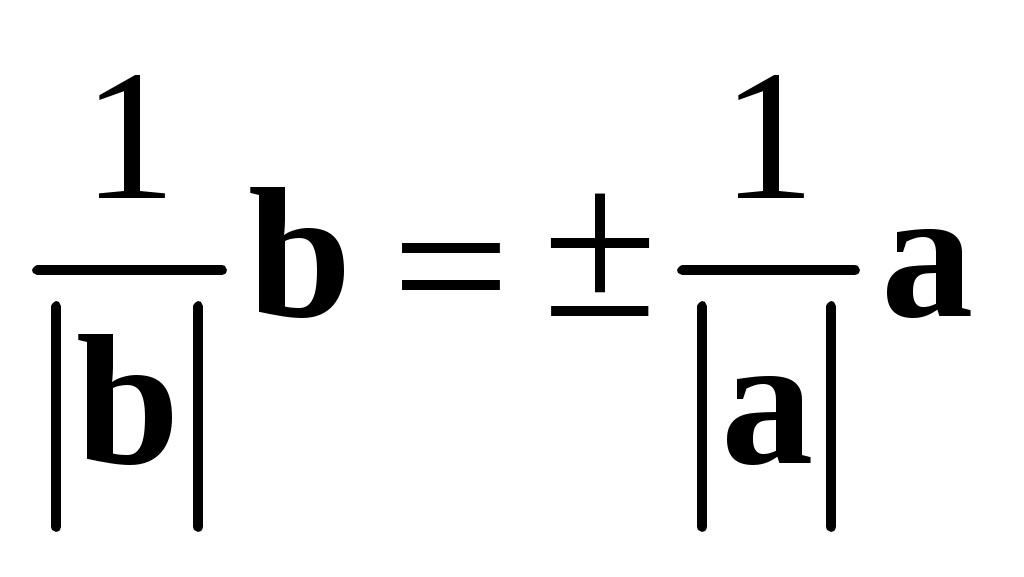 , или , или 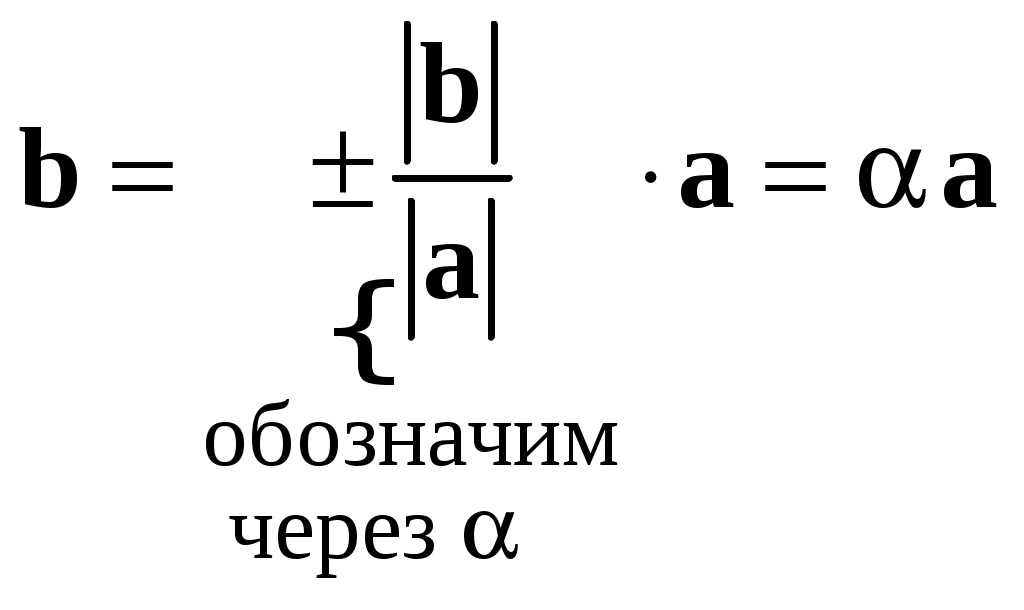 и и  оказывается равным вектору оказывается равным вектору  , умноженному на число , умноженному на число 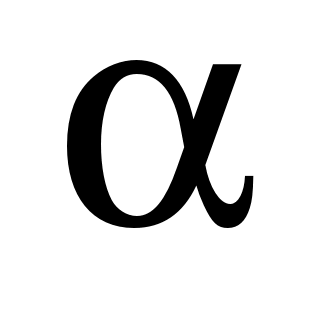 . .
Отметим следующие свойства умножения вектора на число:
3) 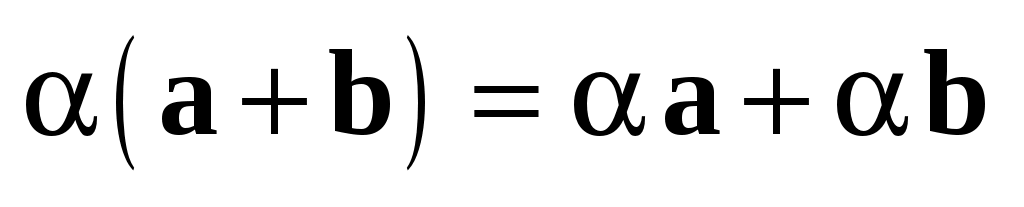 ; ;
4)  ; ;
5) 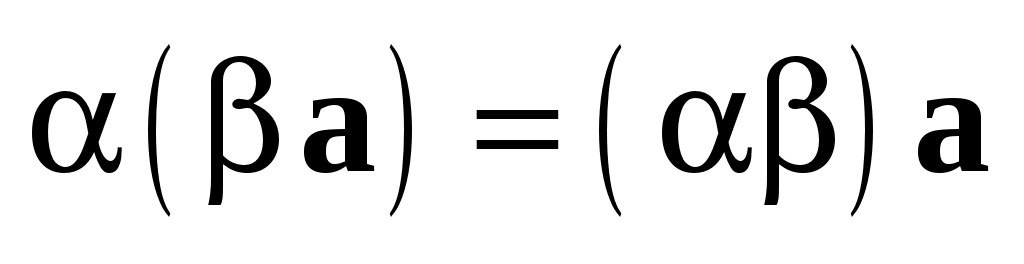 . .
Доказательство свойства 3.
Приложим векторы  и и  к общему началу – произвольной точке к общему началу – произвольной точке 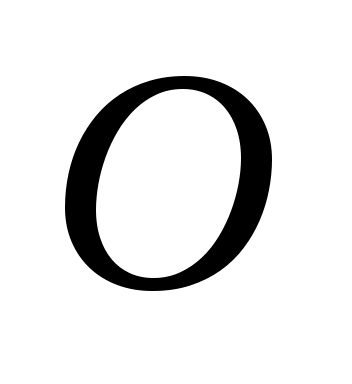 и построим на них как на сторонах параллелограмм (рис. 1.12). и построим на них как на сторонах параллелограмм (рис. 1.12).
И з подобия треугольников з подобия треугольников 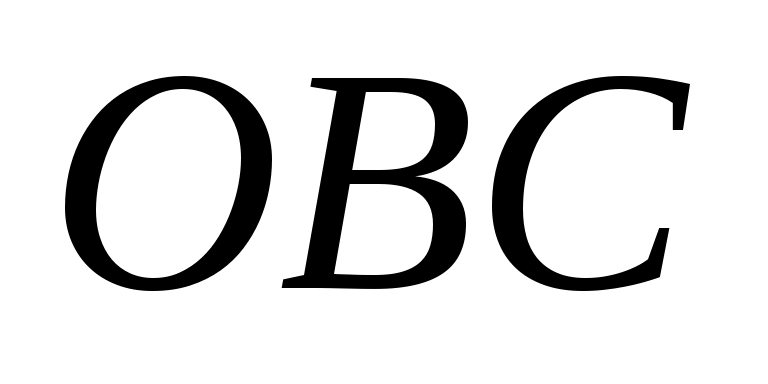 и и 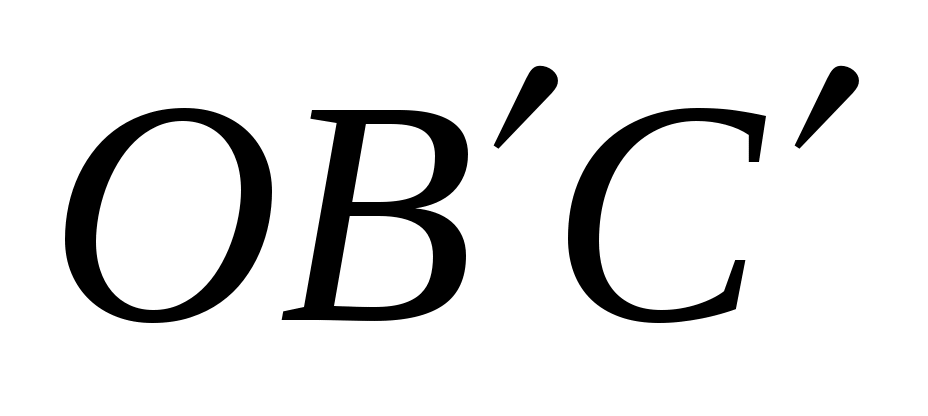 найдем найдем 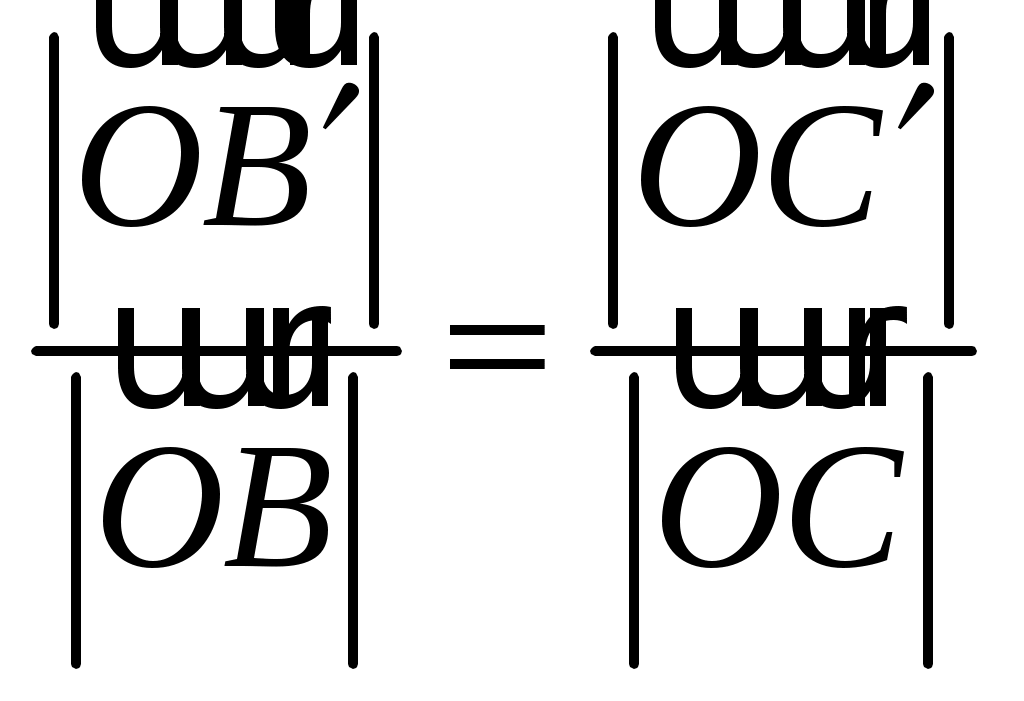 , но , но 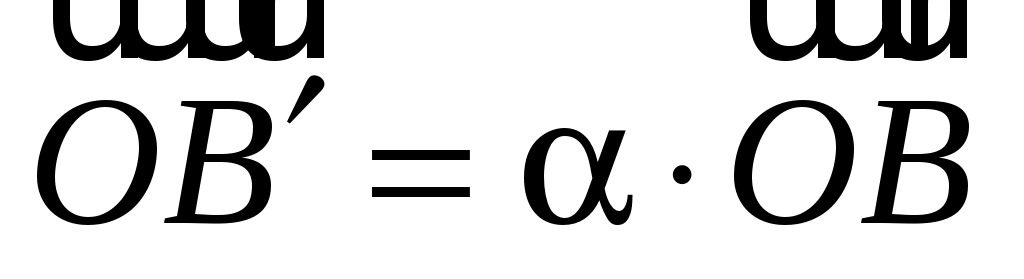 , а тогда , а тогда 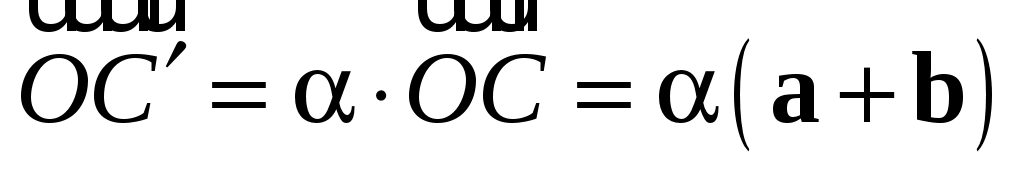 . .
С другой стороны, 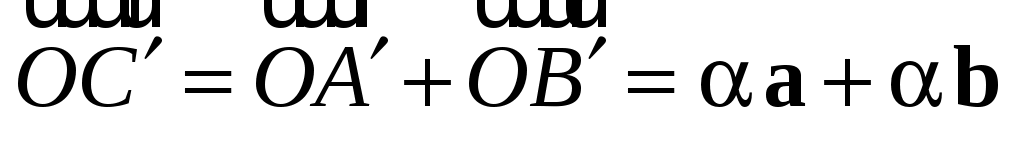 , и свойство 3 доказано. , и свойство 3 доказано.
Свойства 4 и 5 очевидны из наглядных геометрических соображений, и доказательство их опустим.
Совокупность всех геометрических векторов с операциями сложения и умножения на число будем называть пространством геометрических векторов и обозначать 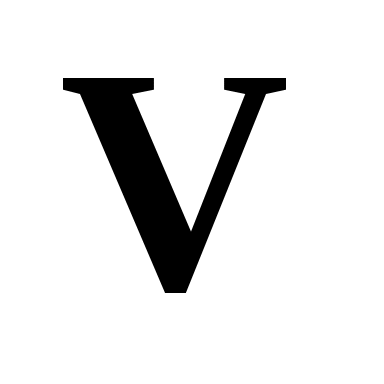 . .
|
|
|
 Скачать 1.47 Mb.
Скачать 1.47 Mb. сли за начало отрезка
сли за начало отрезка 
 пределение 2. Суммой векторов
пределение 2. Суммой векторов  ействительно, в параллелограмме
ействительно, в параллелограмме  оказательство свойства 1.
оказательство свойства 1. риложим вектор
риложим вектор  умма произвольного числа векторов
умма произвольного числа векторов  з определения 3 следует, что если привести векторы
з определения 3 следует, что если привести векторы  амечание 4. Вектор
амечание 4. Вектор 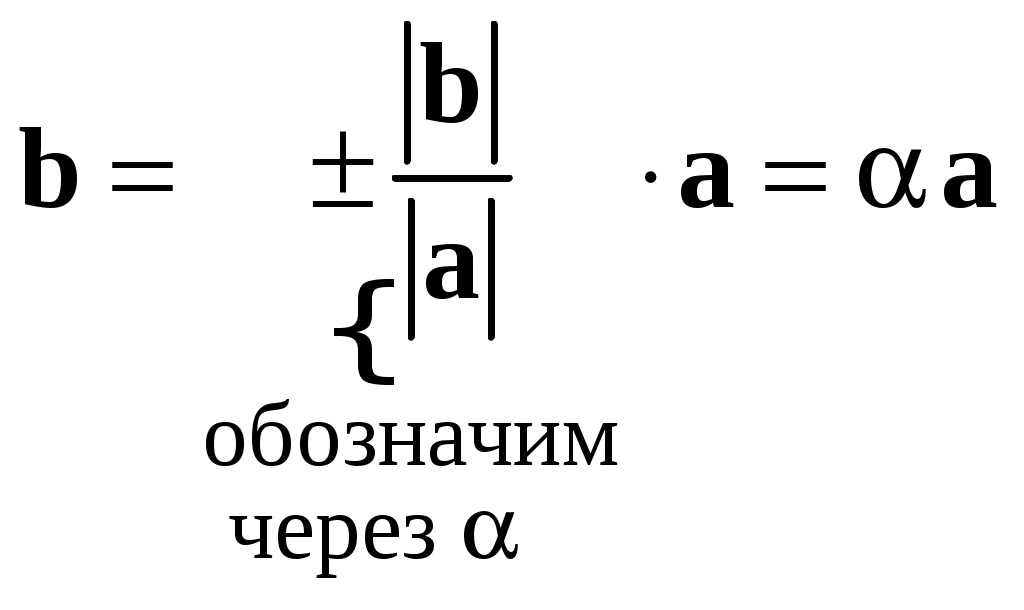 и
и  з подобия треугольников
з подобия треугольников 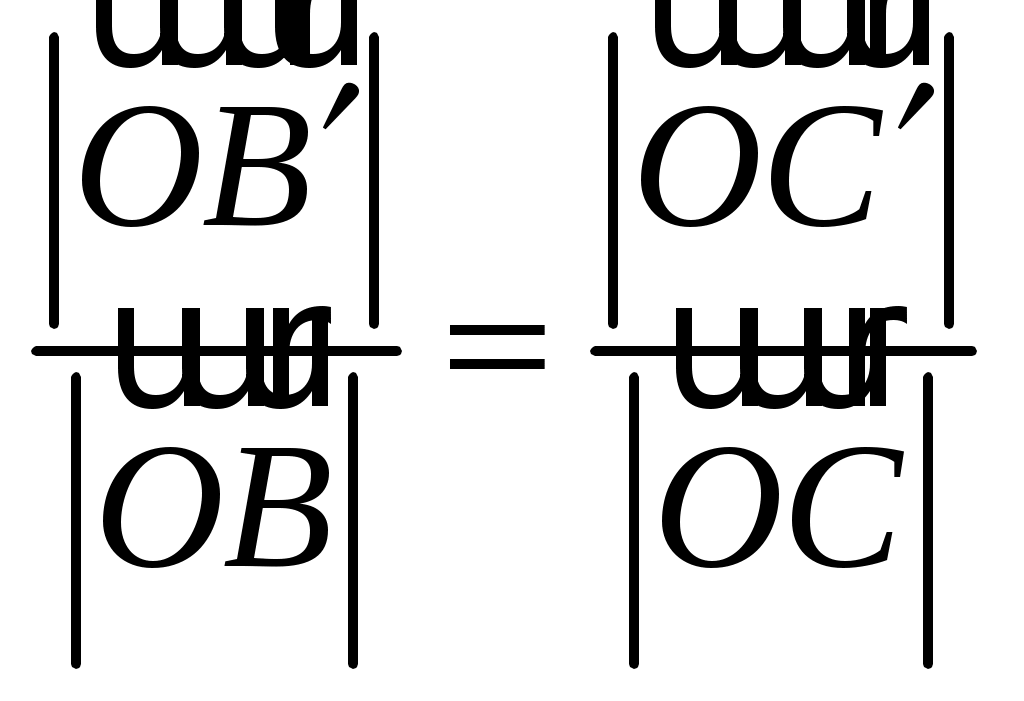 , но
, но 