Следствие 1. Пусть  и и  не коллинеарны, тогда любой вектор не коллинеарны, тогда любой вектор  плоскости можно представить в виде их линейной комбинации (см. доказательство достаточности, случай 3). плоскости можно представить в виде их линейной комбинации (см. доказательство достаточности, случай 3).
Следствие 2. Если три вектора  , ,  и и  не компланарны, они линейно независимы (допустим противоположное, тогда по теореме 4 не компланарны, они линейно независимы (допустим противоположное, тогда по теореме 4  , ,  , ,  компланарны, что противоречит условию). компланарны, что противоречит условию).
Теорема 5. Любые четыре геометрических вектора линейно зависимы.
Доказательство. Пусть  , ,  , ,  и и  – рассматриваемые векторы. – рассматриваемые векторы.
Случай 1. Какие-нибудь три из четырех векторов компланарны, тогда (см. теорему 4), эти три вектора линейно зависимы, следовательно (см. теорему 2), все четыре вектора линейно зависимы, так как содержат зависимую подсистему.
Случай 2. Среди четырех векторов  , ,  , ,  и и  никакие три не компланарны. никакие три не компланарны.
Приведем векторы  , ,  , ,  и и  к одному началу к одному началу 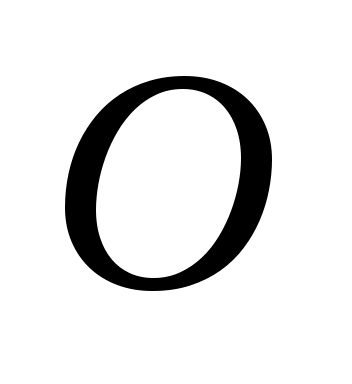 и проведем через конец вектора и проведем через конец вектора  плоскости, соответственно параллельные плоскостям, определяемым парами векторов плоскости, соответственно параллельные плоскостям, определяемым парами векторов  и и  , ,  и и  , ,  и и  . .
Точки пересечения этих плоскостей с прямыми, на которых лежат  , ,  и и  , обозначим , обозначим  , , 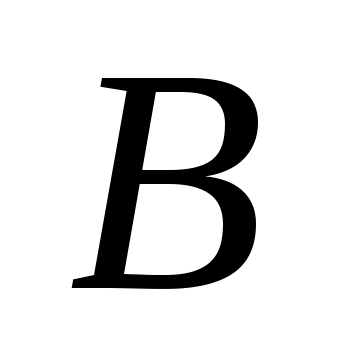 и и 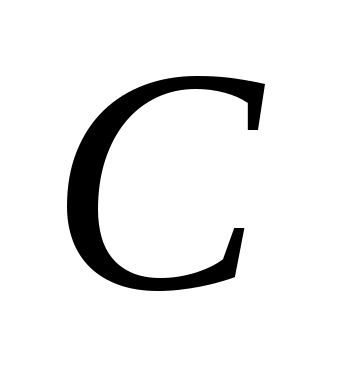 соответственно (рис. 1.15). соответственно (рис. 1.15).
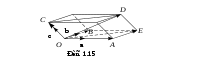
Из параллелограмма  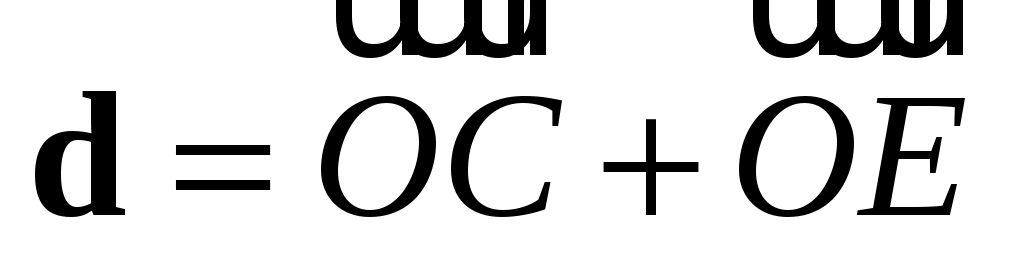 , аналогично из параллелограмма , аналогично из параллелограмма   и, таким образом, и, таким образом,
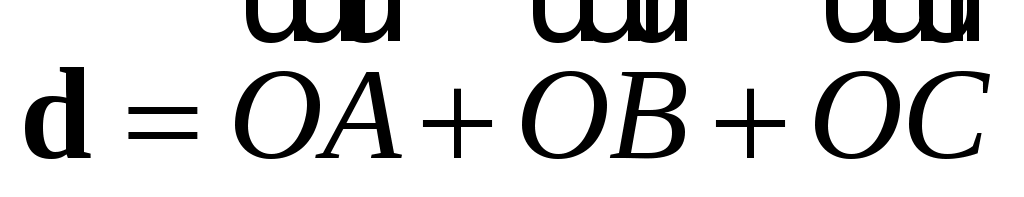 . (1.8) . (1.8)
Вектор  коллинеарен коллинеарен  , следовательно, найдется число , следовательно, найдется число 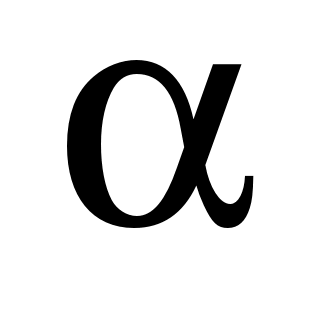 такое, что такое, что
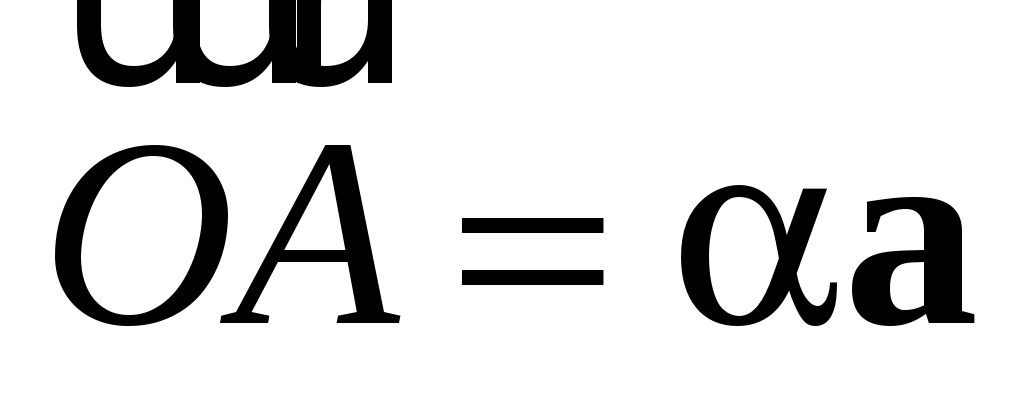 . .
Вектор  коллинеарен коллинеарен  , следовательно, найдется число , следовательно, найдется число 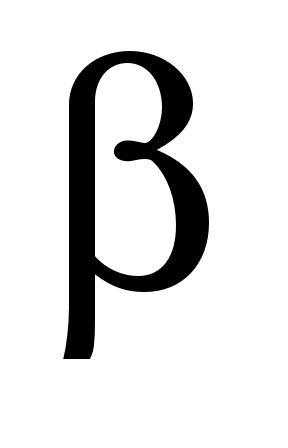 такое, что такое, что
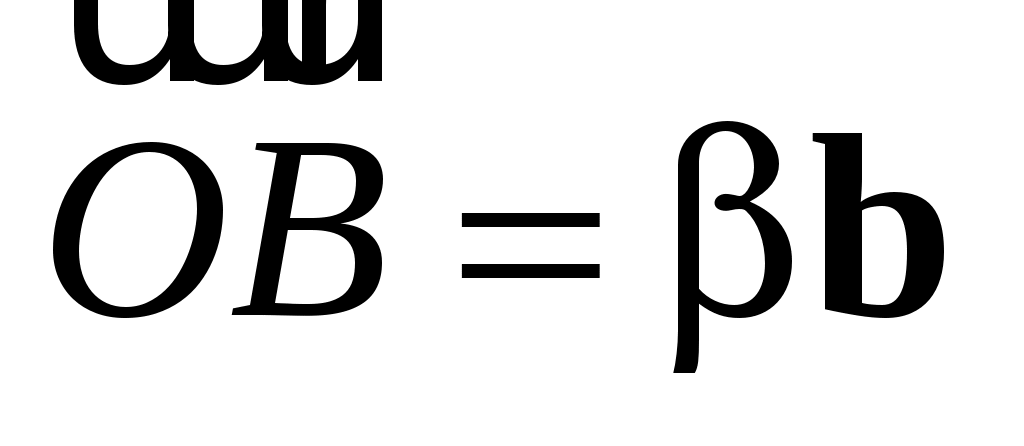 . .
Вектор 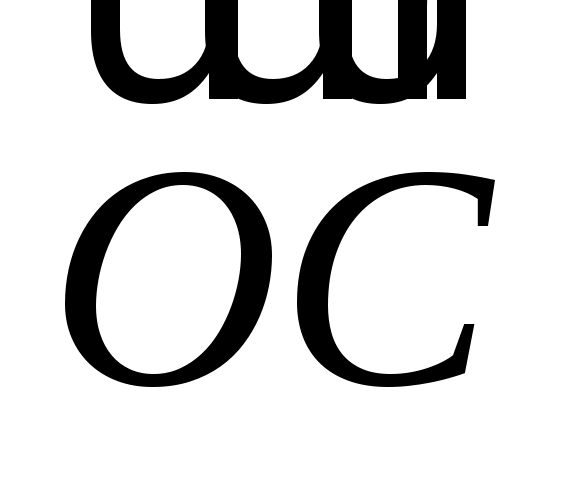 коллинеарен коллинеарен 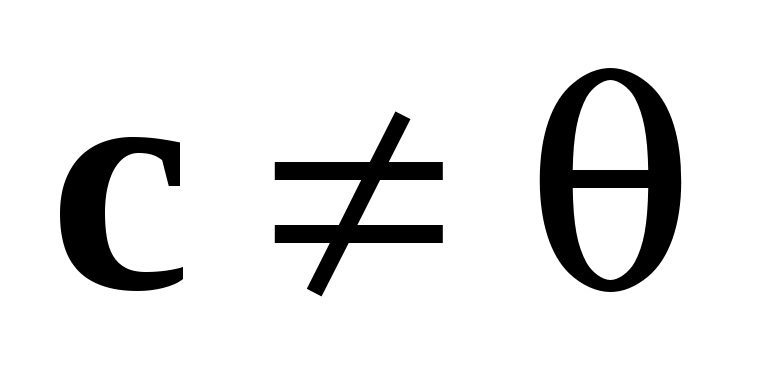 , следовательно, найдется число , следовательно, найдется число 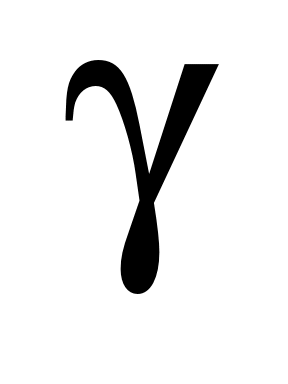 такое, что такое, что
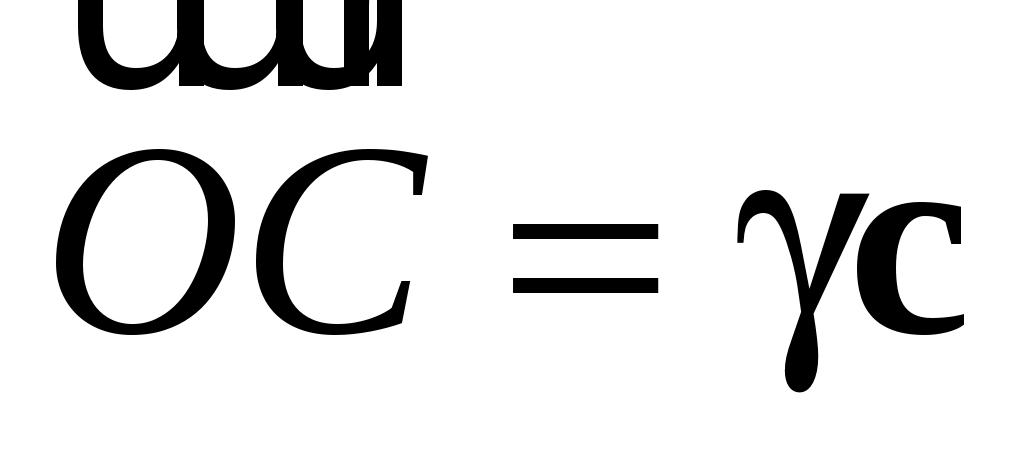 . .
Подставив полученные результаты в (1.8), найдем
 , ,
или
 . (1.9) . (1.9)
Равенство (1.9) означает линейную зависимость векторов  , ,  , ,  и и  : их линейная комбинация с коэффициентами, не равными нулю одновременно (коэффициент при : их линейная комбинация с коэффициентами, не равными нулю одновременно (коэффициент при  равен равен  и отличен от нуля), равна и отличен от нуля), равна 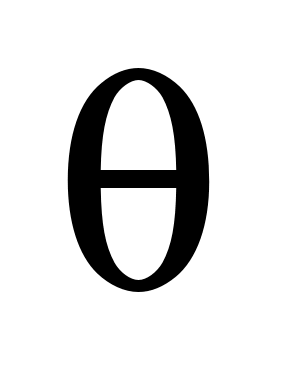 . .
Следствие. Каковы бы ни были некомпланарные векторы  , ,  и и  , любой вектор , любой вектор  можно представить в виде их линейной комбинации можно представить в виде их линейной комбинации
1.3. Понятие базиса. Координаты вектора
и их свойства
Определение 8. Три вектора  , ,  , ,  называются базисом в называются базисом в 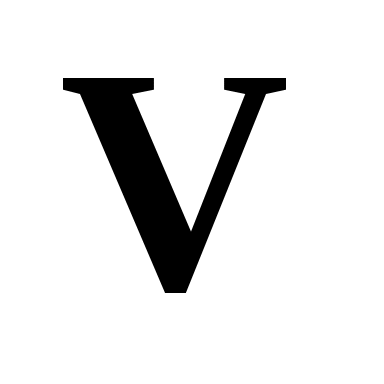 , если: , если:
1)  , ,  , ,  линейно независимы; линейно независимы;
2) любой вектор  можно представить в виде их линейной комбинации, т.е. найдутся числа можно представить в виде их линейной комбинации, т.е. найдутся числа 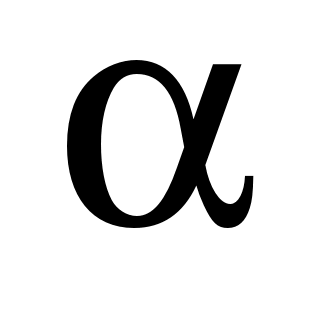 , , 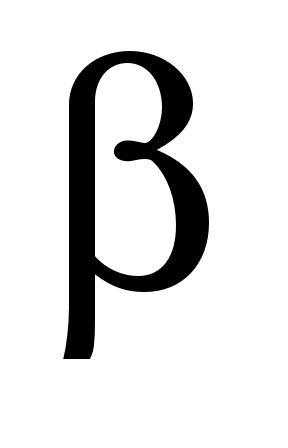 и и 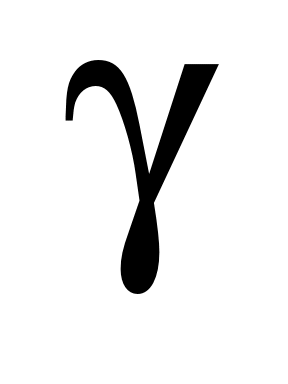 такие, что такие, что  . .
Определение 9. Два вектора  и и  называются базисом в плоскости, если: называются базисом в плоскости, если:
1)  и и  линейно независимы; линейно независимы;
2) для любого вектора  этой плоскости найдутся числа этой плоскости найдутся числа и и 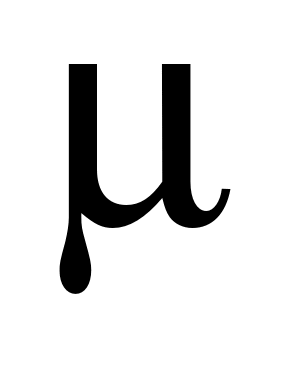 такие, что такие, что  можно представить в виде их линейной комбинации можно представить в виде их линейной комбинации  и и  , т.е. найдутся числа , т.е. найдутся числа  и и 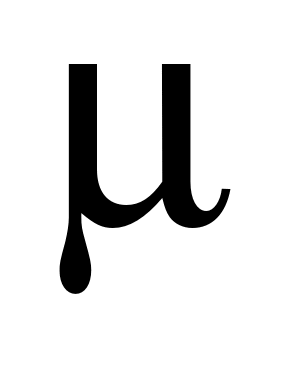 такие, что такие, что 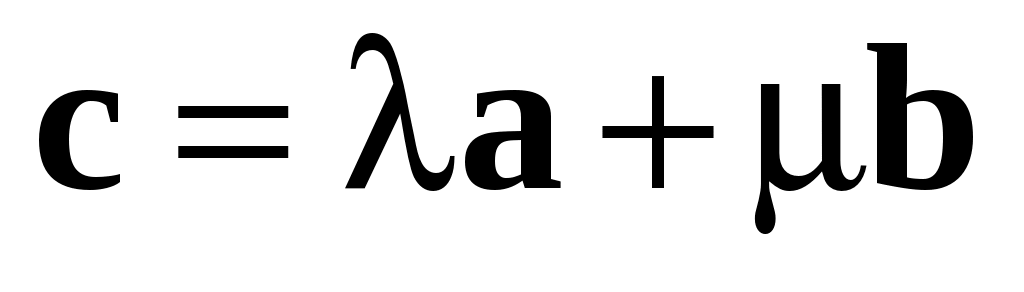 . .
Из результатов, полученных в 1.2, следует, что любые три некомпланарных вектора составляют базис в 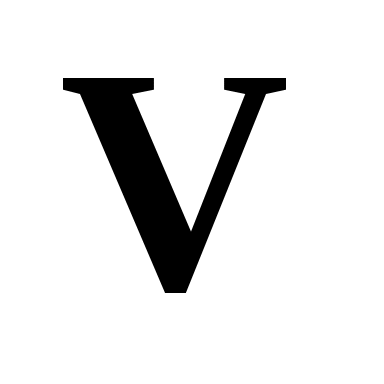 . .
В самом деле, пусть  , ,  и и  не компланарны. Тогда согласно следствию 2 из теоремы 4 векторы не компланарны. Тогда согласно следствию 2 из теоремы 4 векторы  , ,  и и  линейно независимы. А в силу следствия из теоремы 5 любой вектор линейно независимы. А в силу следствия из теоремы 5 любой вектор  может быть представлен в виде линейной комбинации может быть представлен в виде линейной комбинации  , ,  и и  , и, таким образом, , и, таким образом,  , ,  и и  являются базисом в являются базисом в 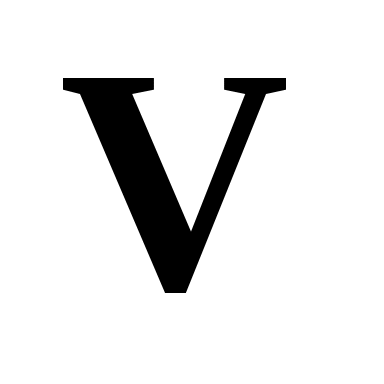 (в соответствии с определением 8). (в соответствии с определением 8).
Аналогично любые два неколлинеарных вектора образуют базис в плоскости.
Действительно, если  и и  не коллинеарны, то согласно следствию из теоремы 3 не коллинеарны, то согласно следствию из теоремы 3  и и  линейно независимы. А в силу следствия 1 из теоремы 4 любой вектор линейно независимы. А в силу следствия 1 из теоремы 4 любой вектор  плоскости может быть представлен в виде их линейной комбинации и, следовательно, плоскости может быть представлен в виде их линейной комбинации и, следовательно,  , ,  - базис плоскости (в соответствии с определением 9). - базис плоскости (в соответствии с определением 9).
Ограничимся в дальнейшем рассмотрением базиса в пространстве.
Пусть  , ,  , ,  – произвольный базис в – произвольный базис в 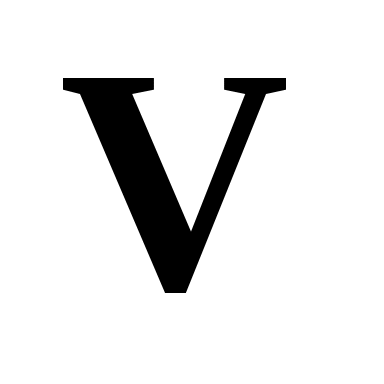 , ,  . Тогда . Тогда
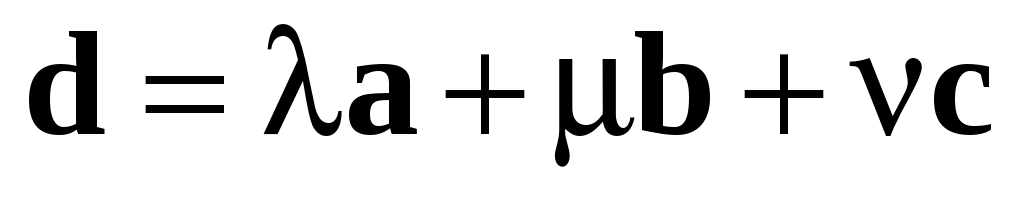 (1.10) (1.10)
Правая часть равенства (1.10) называется разложением вектора  по базису по базису  , ,  , ,  , а числа , а числа  , , 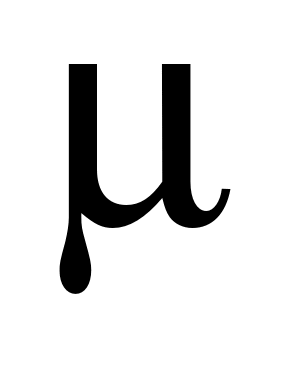 , , 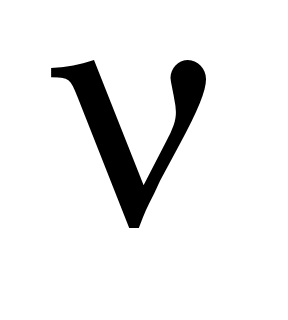 – координатами вектора – координатами вектора  относительно базиса относительно базиса  , ,  , ,  . .
Теорема 6. Пусть  , ,  , ,  – базис в – базис в 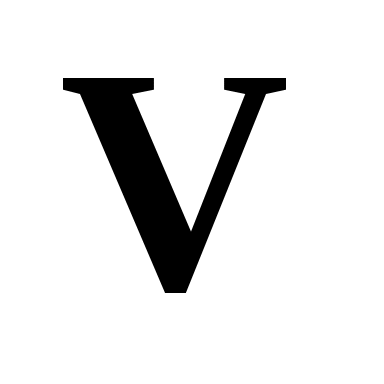 . Координаты любого вектора . Координаты любого вектора  относительно базиса относительно базиса  , ,  , ,  определяются однозначно. определяются однозначно.
Доказательство. Доказательство проведем от противного.
Допустим, существует другое разложение вектора  по базису по базису  , ,  , ,  : :

Противоположный вектор 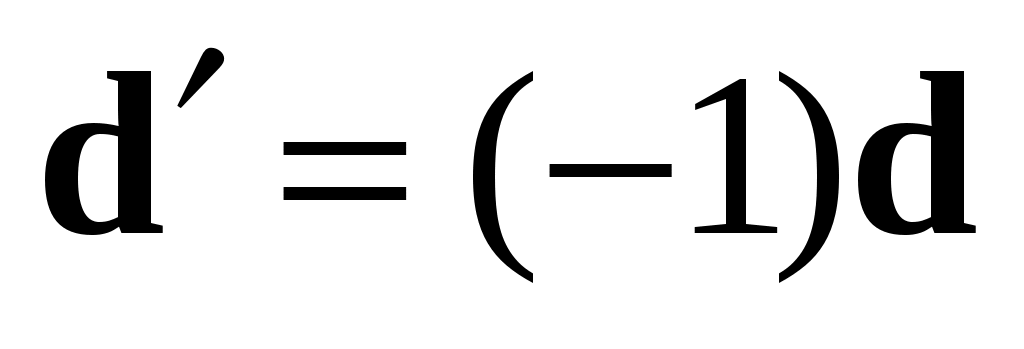 (см. замечание 4). К обеим частям равенства (1.10) прибавим вектор (см. замечание 4). К обеим частям равенства (1.10) прибавим вектор
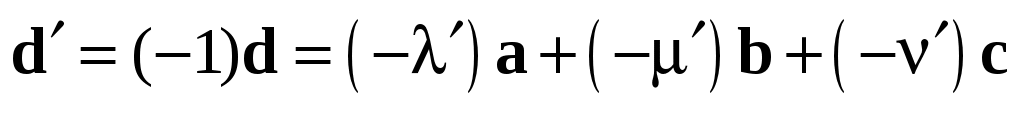
и получим
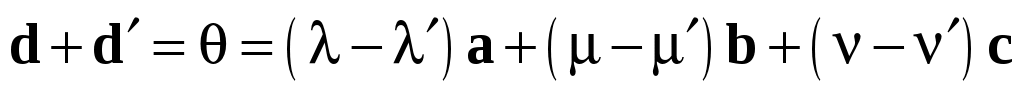 . (1.11) . (1.11)
Равенство (1.11) означает, что линейная комбинация векторов  , ,  , ,  равна равна 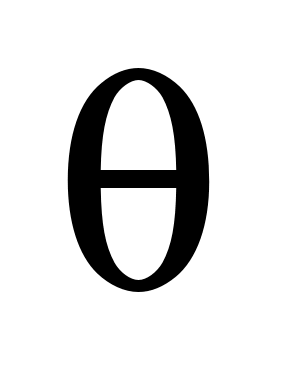 , откуда в силу линейной независимости , откуда в силу линейной независимости  , ,  и и  следует, что коэффициенты при следует, что коэффициенты при  , ,  и и  равны нулю, а тогда равны нулю, а тогда 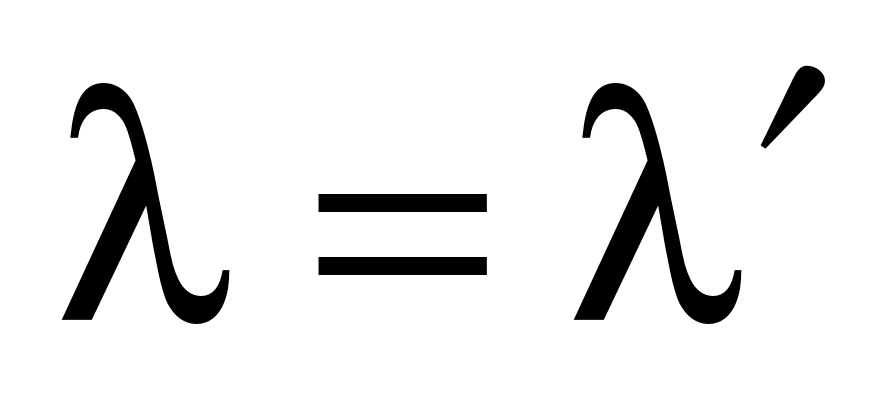 , , 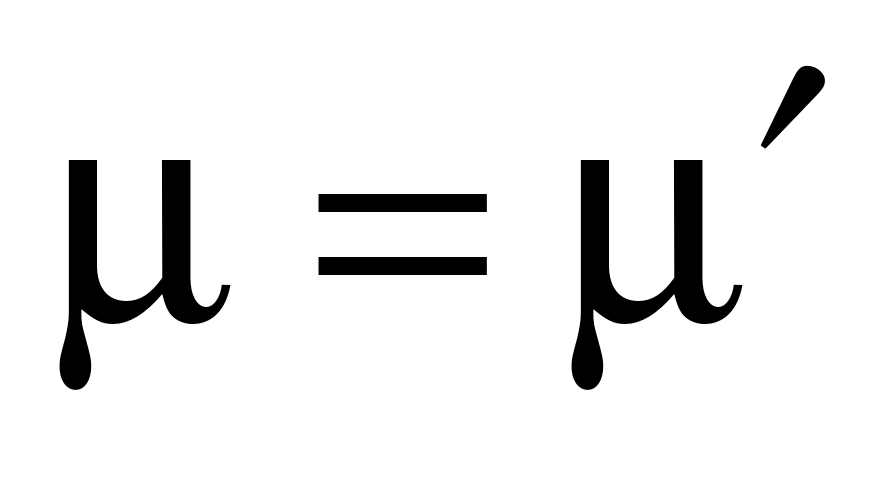 , ,  . .
|
 Скачать 1.47 Mb.
Скачать 1.47 Mb.
