Все задачи. Решение Как известно, базисом в пространстве является любая упорядоченная система из трёх линейно независимых векторов. Покажем, что векторы, и линейно независимы, т е. выполняется равенство

• Название: Решение Как известно, базисом в пространстве является любая упорядоченная система из трёх линейно независимых векторов. Покажем, что векторы, и линейно независимы, т е. выполняется равенство
• Анкор: Все задачи.doc
• Дата: 28.01.2018
• Размер: 1 Mb.
• Имя файла: Все задачи.doc
• Тип: Решение; #14969
• Категория: Математика
• страница: 1 из 3

Задача 04. Даны четыре вектора (а₁, а₂, а₃), (b₁, b₂, b₃),

(c₁, c₂, c₃) и (d₁, d₂, d₃) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.

(1,3,5), (0,2,0), (5,7,9), (0,4,16).

Решение: Как известно, базисом в пространстве является любая упорядоченная система из трёх линейно независимых векторов. Покажем, что векторы , и линейно независимы, т.е. выполняется равенство:



при условии, что все числа , , одновременно равны нулю. Подставляя в это равенство координаты векторов , , , получаем:

(е₁ + 3е₂ + 5е₃) + (2е₂) + (5е₁ + 7е₂ + 9е₃) = 0

или ( + 5) ∙ е₁ + (3 + + 7) ∙ е₂ +(5 + 9) ∙ е₃ = 0

Для того, чтобы вектор, разложенный по базису е₁, е₂, е₃ был равен нулевому вектору, его координаты должны равняться нулю, т.е.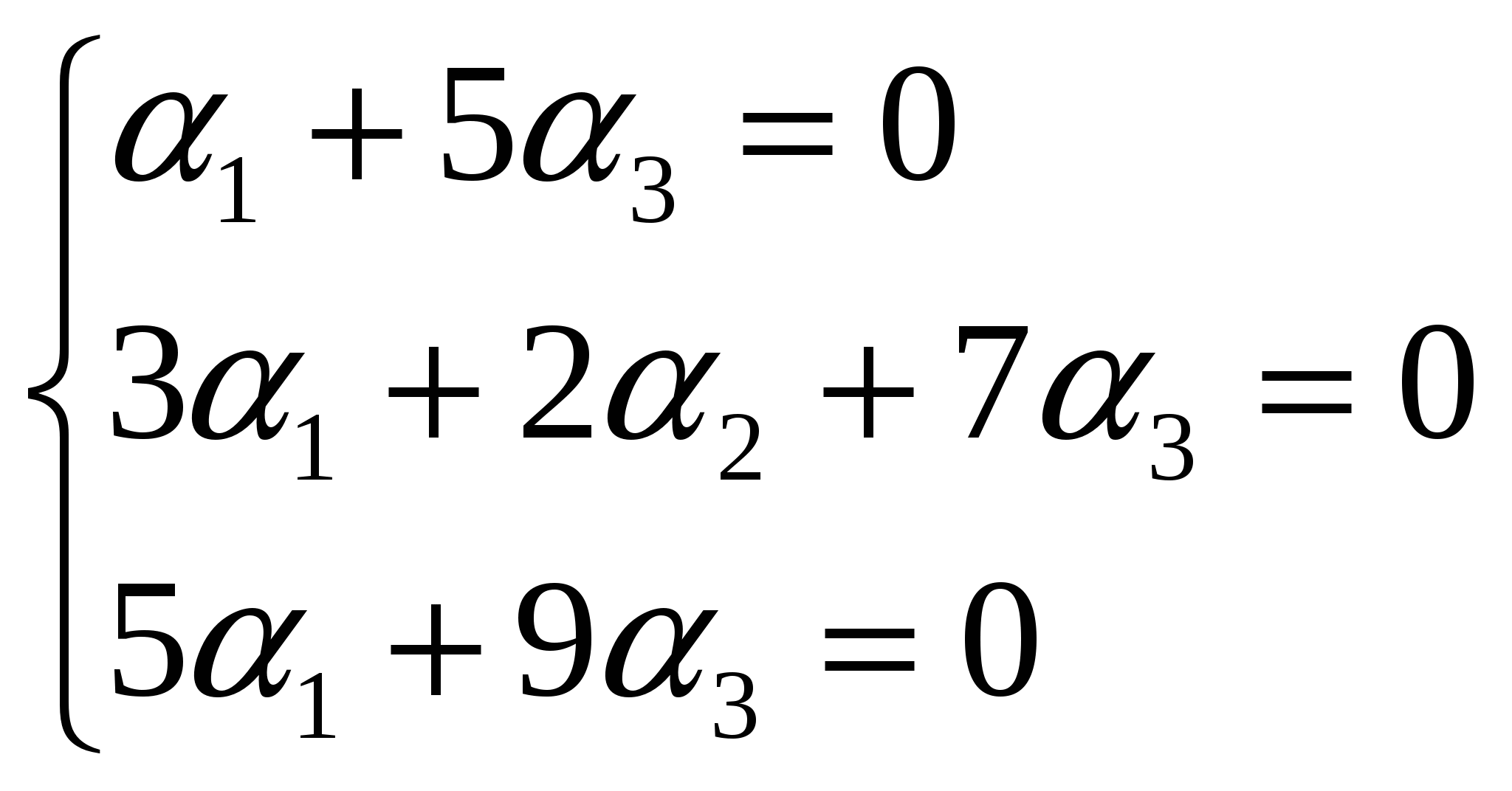



Получим однородную систему трех линейных уравнений с тремя неизвестными , , . Такая система имеет нулевое решение (=0, =0, =0), если её определитель не равен нулю.

Поскольку ,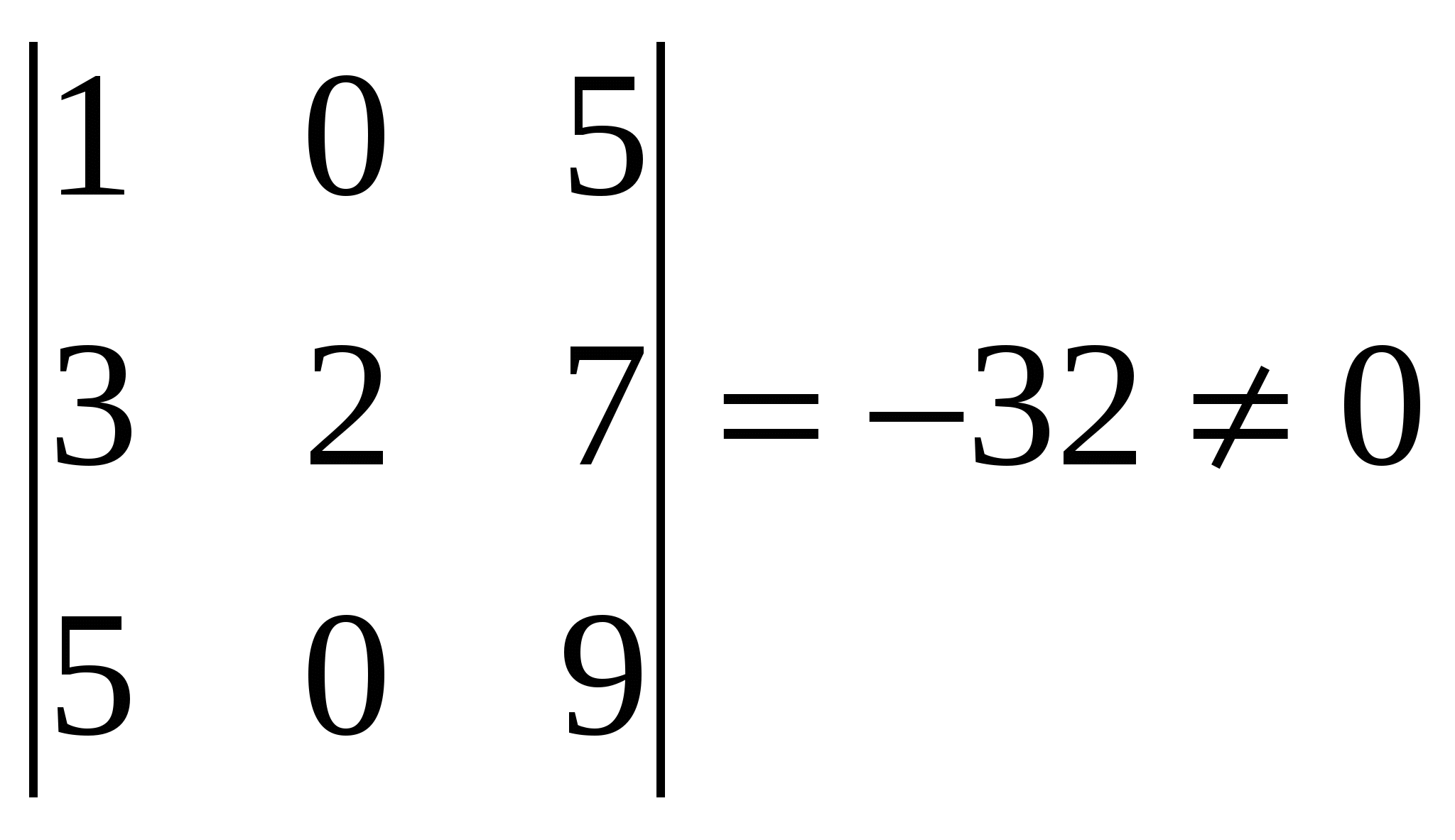

то векторы , , линейно независимы. Следовательно, они образуют базис и вектор является линейной комбинацией векторов , , : =. Числа , , будут координатами вектора в базисе , , . Найдем их.

Воспользовавшись разложением , , , в базисе е₁, е₂, е₃, имеем:

4 е₂ + 16 е₃ = ( е₁ + 3 е₂ + 5 е₃) + (2 е₂) + (5 е₁ + 7 е₂ + 9 е₃)

Или 4 е₂ + 16 е₃ = ( + 5) е₁ + (3 + 2 + 7) е₂ + (5+ 9) е₃.

Из равенства векторов следует равенство их координат, поэтому получаем систему: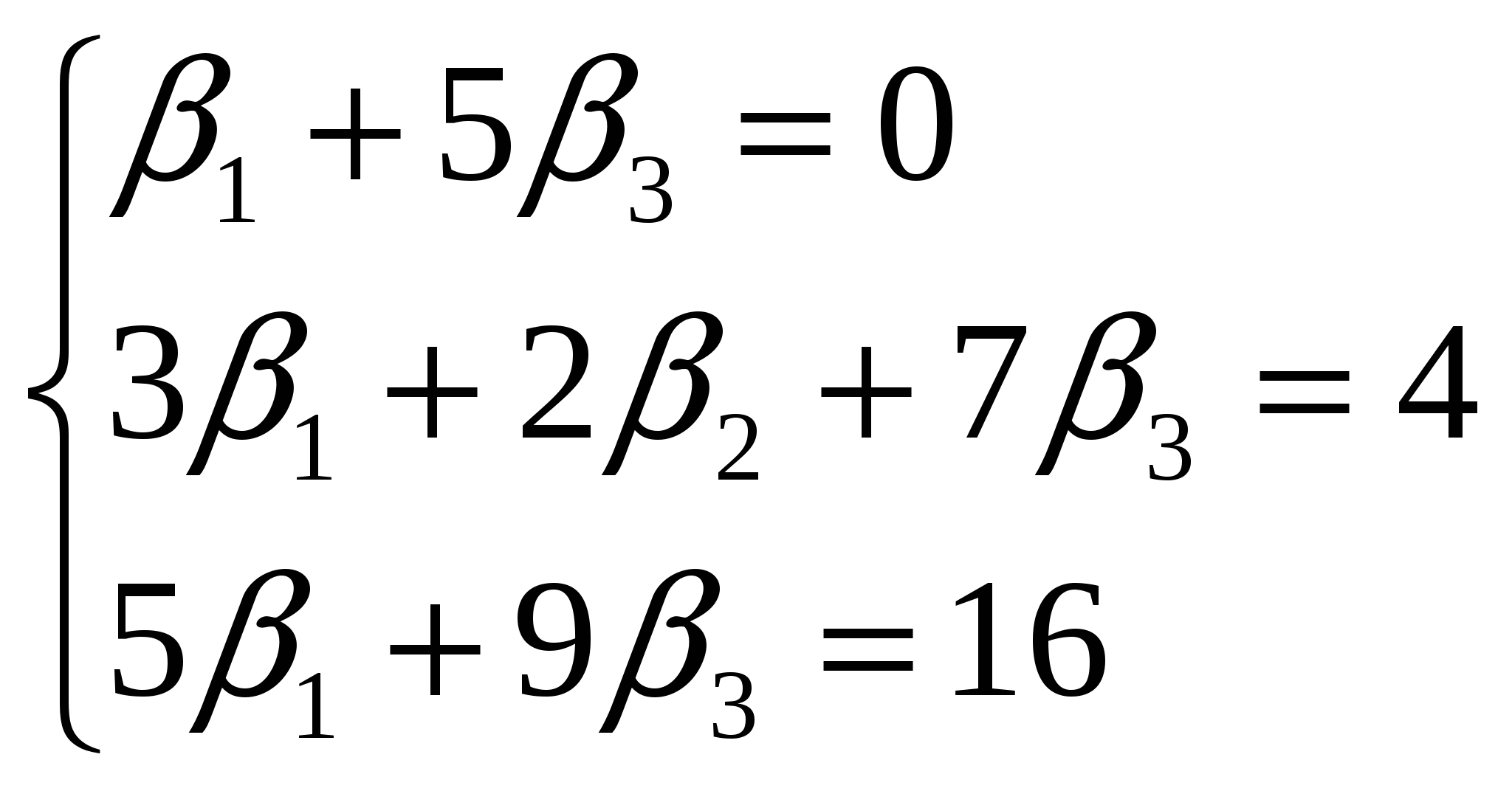



Решая её по формулам Крамера 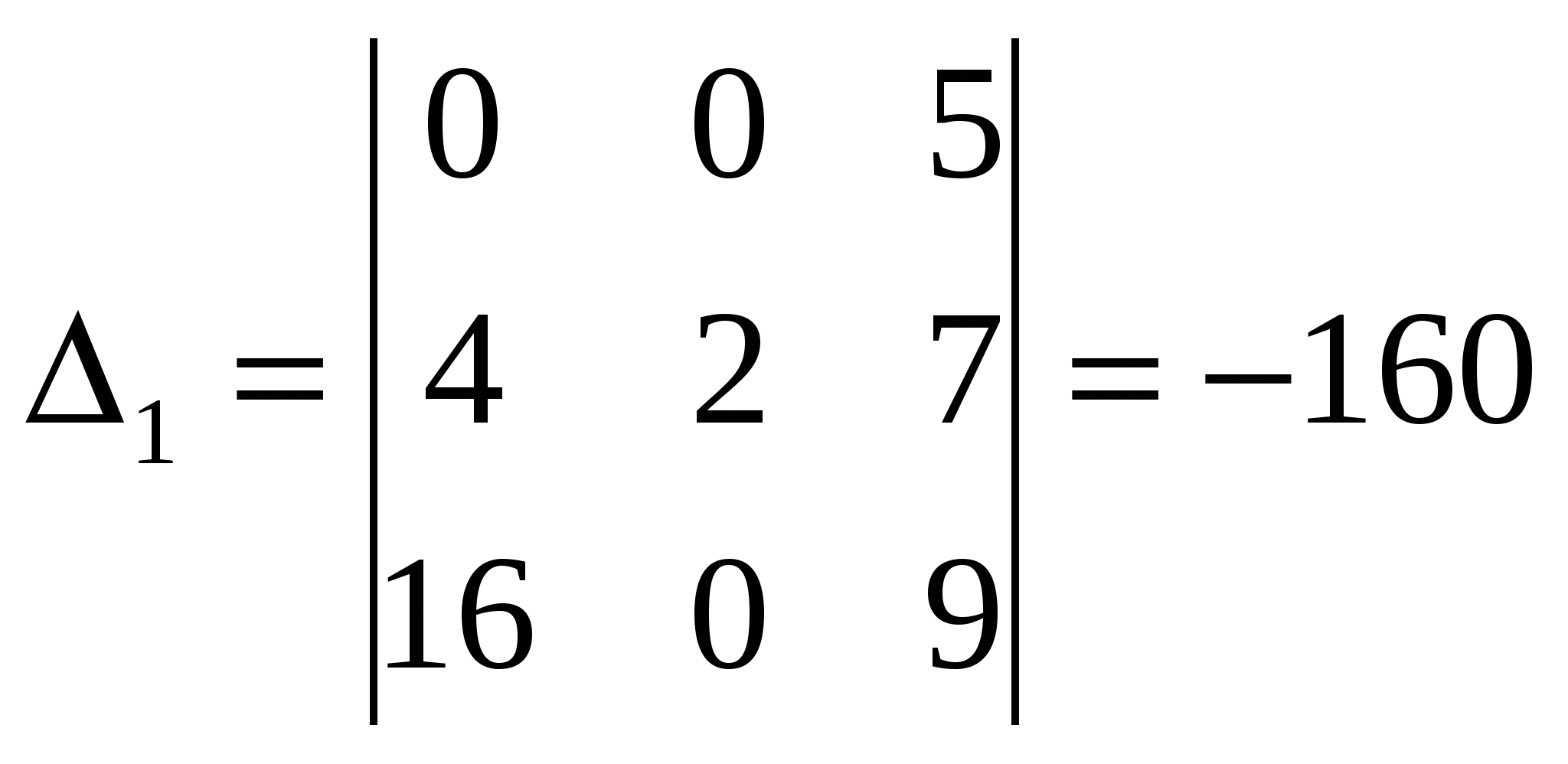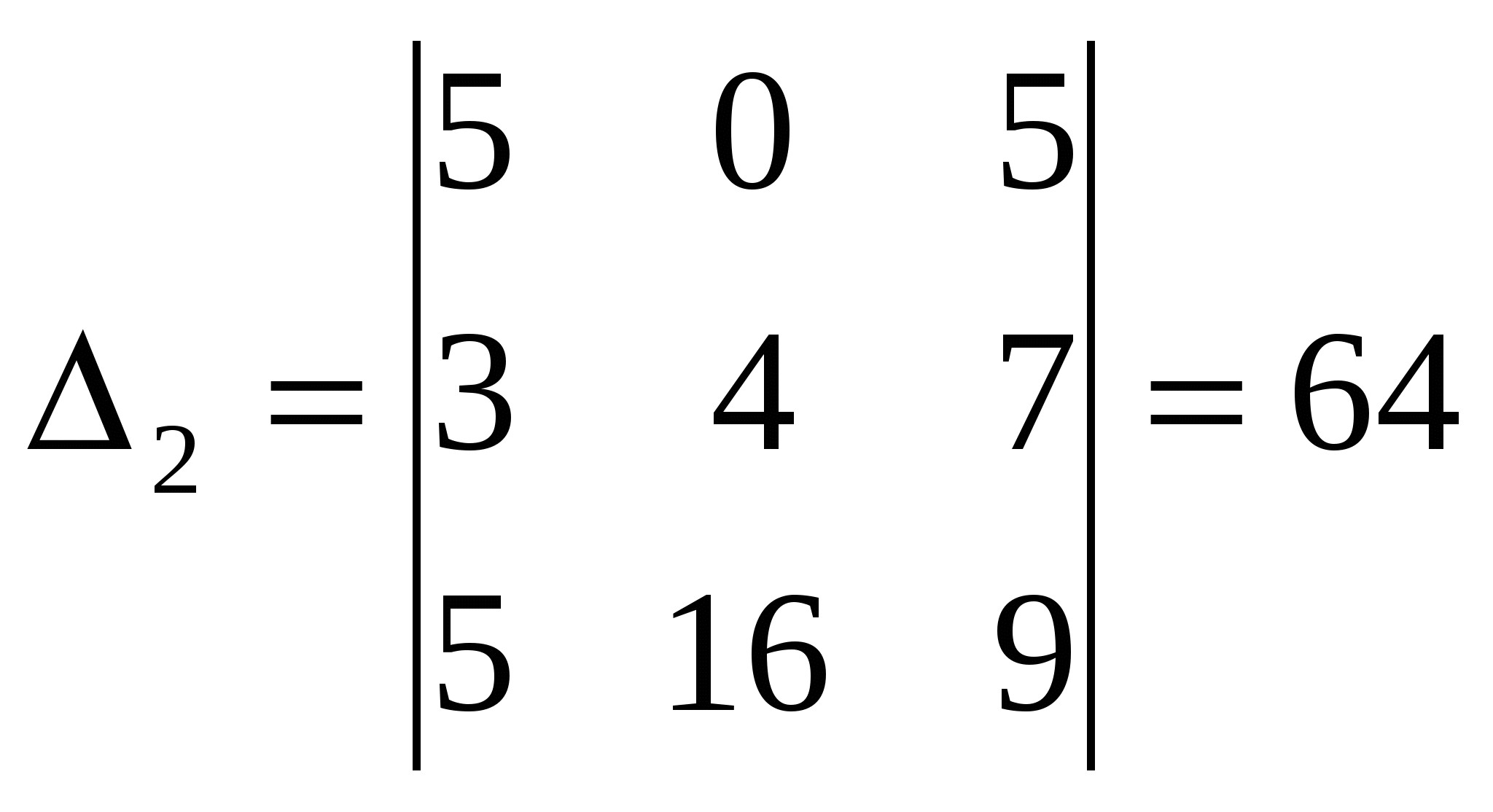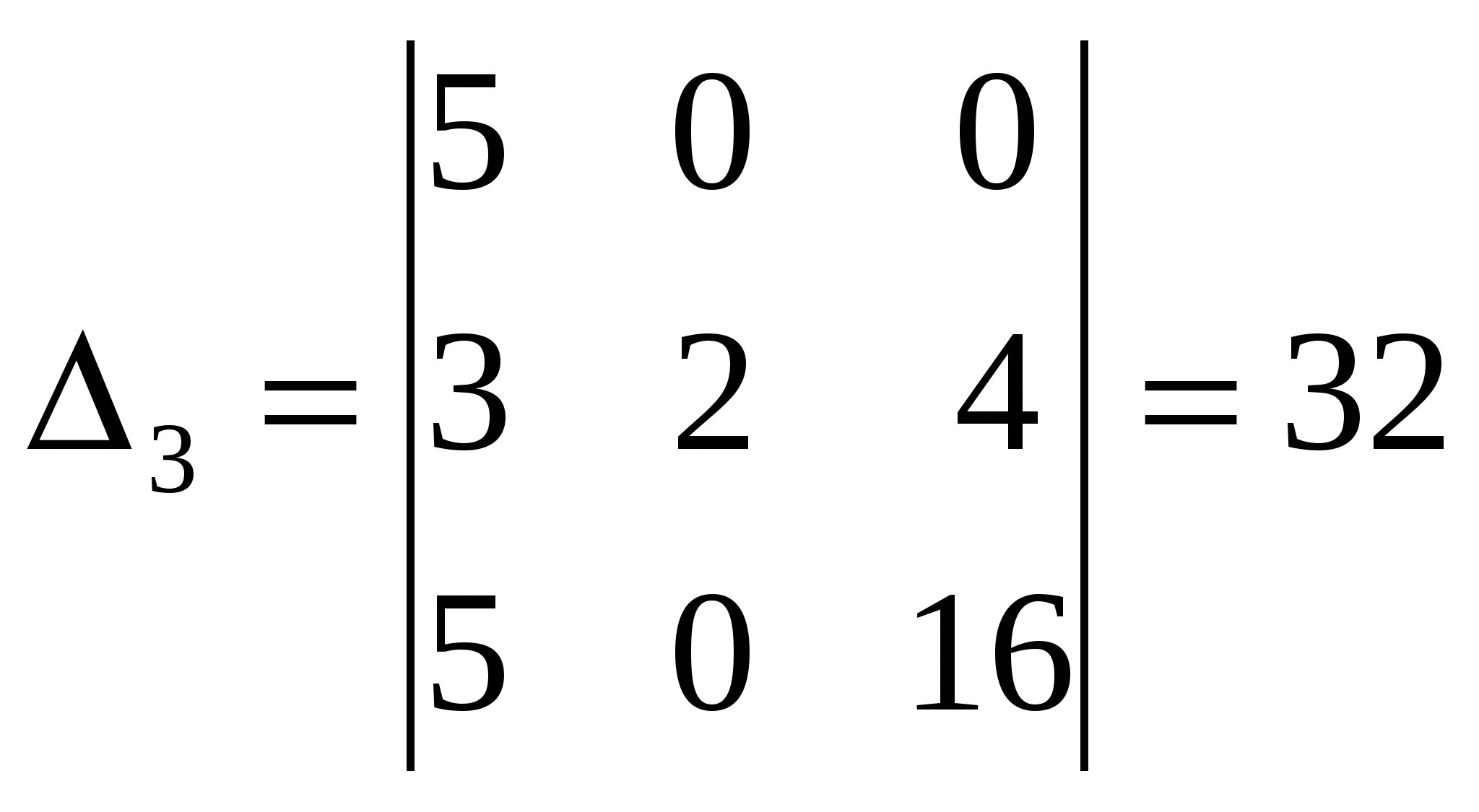=, , находим:

, , .

Следовательно, , , , т.е. координаты вектора в этом базисе: =(1,-1,0).

Задача 14. Даны координаты вершин пирамиды A₁A₂A₃A₄. Найти:

1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнения прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

Сделать чертёж.

А₁(2,4,3), А₂(7,6,3), А₃(4,9,3), А₄(3,6,7).
Решение:

1. 
   найдём координаты и длину вектора:
   

= (5,2,0),

2. 
   найдем угол между ребрами А₁А₂ и А₁А_4.
   

Для этого найдём координаты и длину вектора :

= (1,2,4),

Векторное произведение векторов: 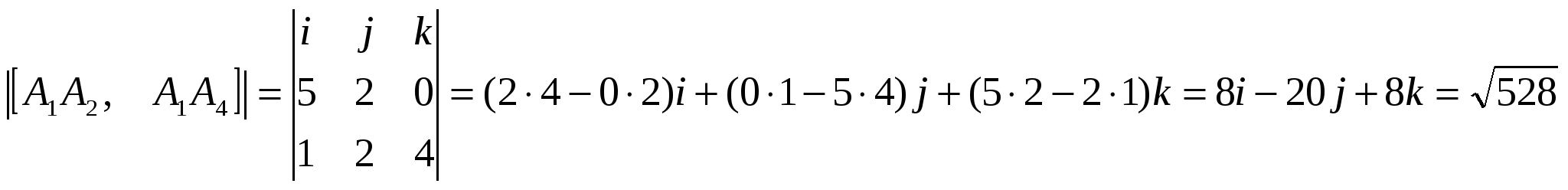и :



;

3. 
   угол между ребром А₁А₄ и гранью А₁А₂А₃
   

найдем каноническое уравнение ребра А₁А₄

,



– каноническое уравнение ребра А₁А₄

Найдем уравнение плоскости, проходящей через точки

А₁(2,4,3), А₂(7,6,3), А₃(4,9,3):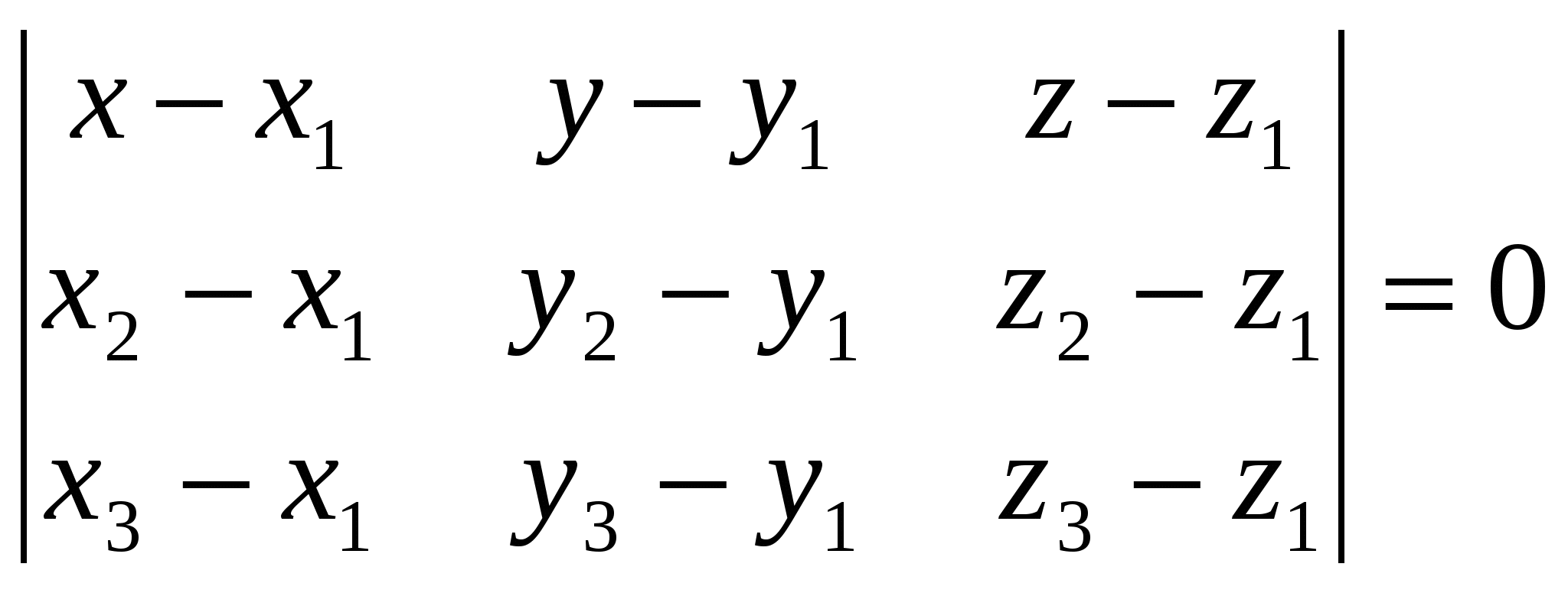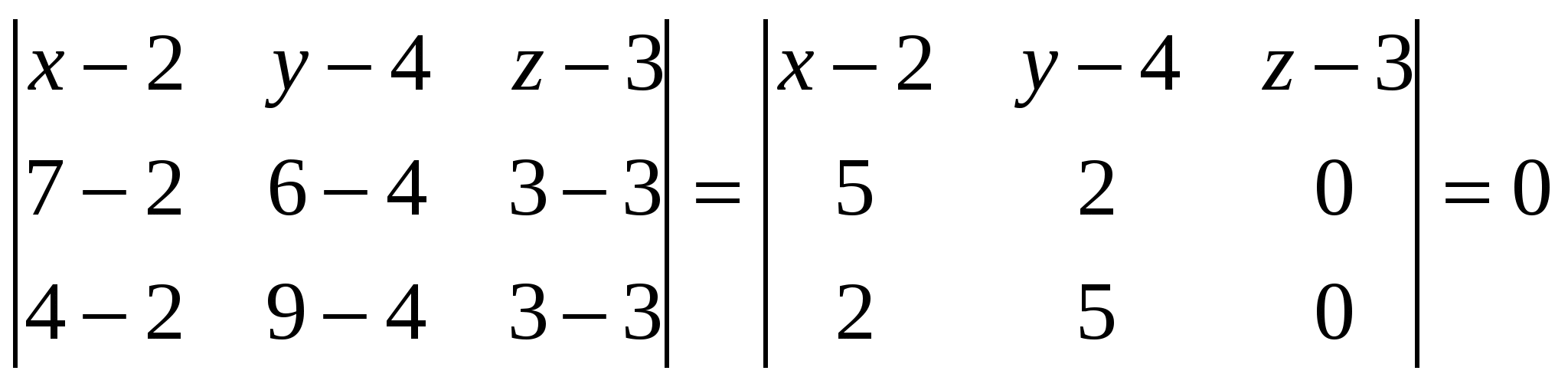







уравнение плоскости, проходящей через точки А₁, А₂, А₃:



Синус угла между ребром А₁А₄ и гранью А₁А₂А₃

4. 
   площадь грани А₁А₂А₃;
   

Грань А₁А₂А₃ – это треугольник, площадь которого равна ½ площади параллелограмма, построенного на векторах и

= (5,2,0),

= (2,5,0),

Векторное произведение векторов:





Находим площадь треугольника А₁А₂А₃:


5) объём пирамиды;


= (5,2,0),

= (2,5,0),

= (1,2,4),

Смешанное произведение векторов: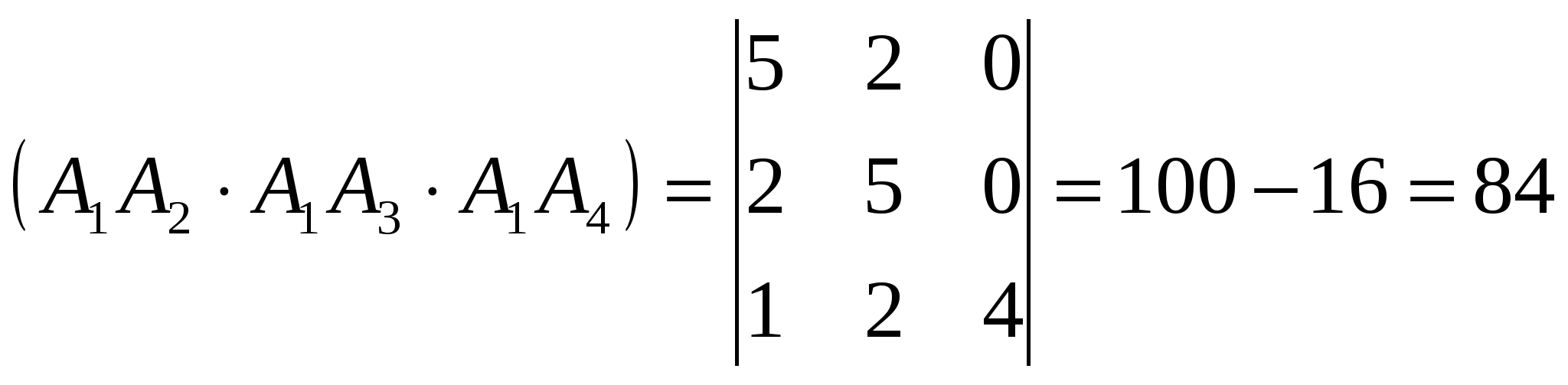



объём пирамиды

6) уравнения прямой А₁А₂;

а). Как пересечение двух плоскостей А₁А₂А₃ и А₁А₂А₄:

уравнение плоскости, проходящей через точки А₁, А₂, А₃:



Найдем уравнение плоскости, проходящей через точки

А₁(2,4,3), А₂(7,6,3), А₄(3,6,7):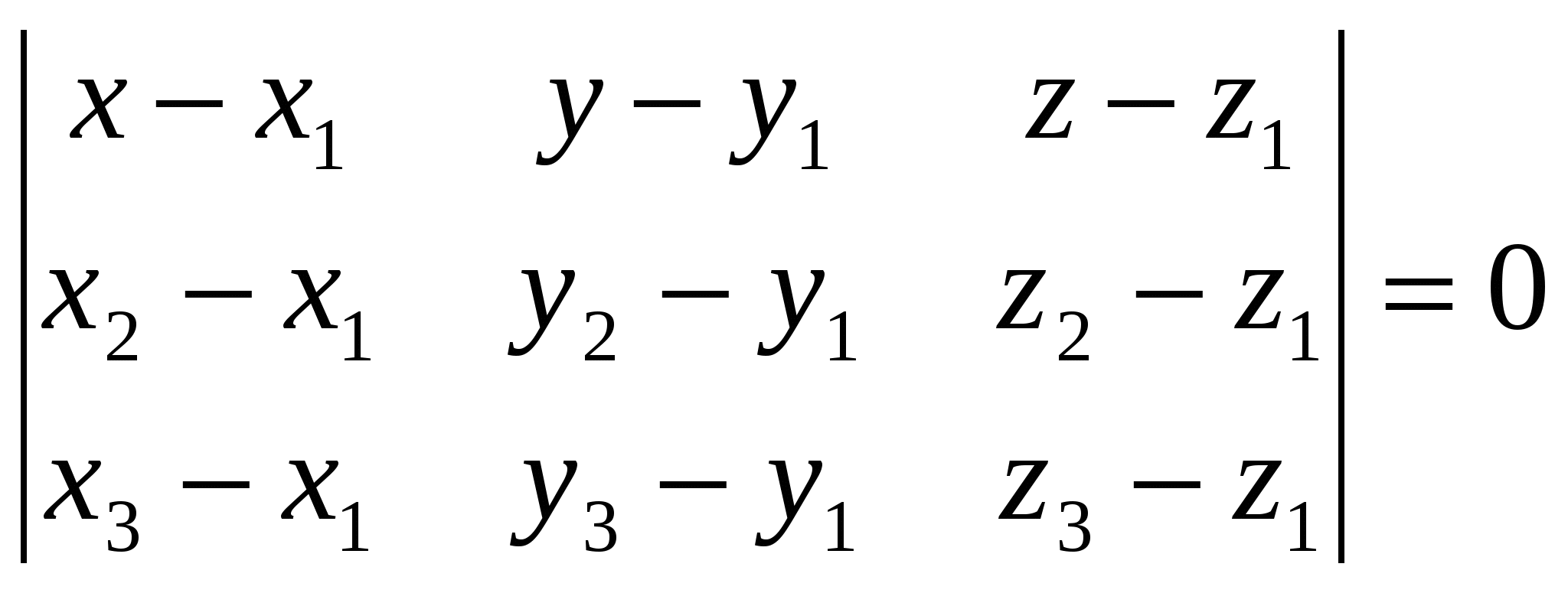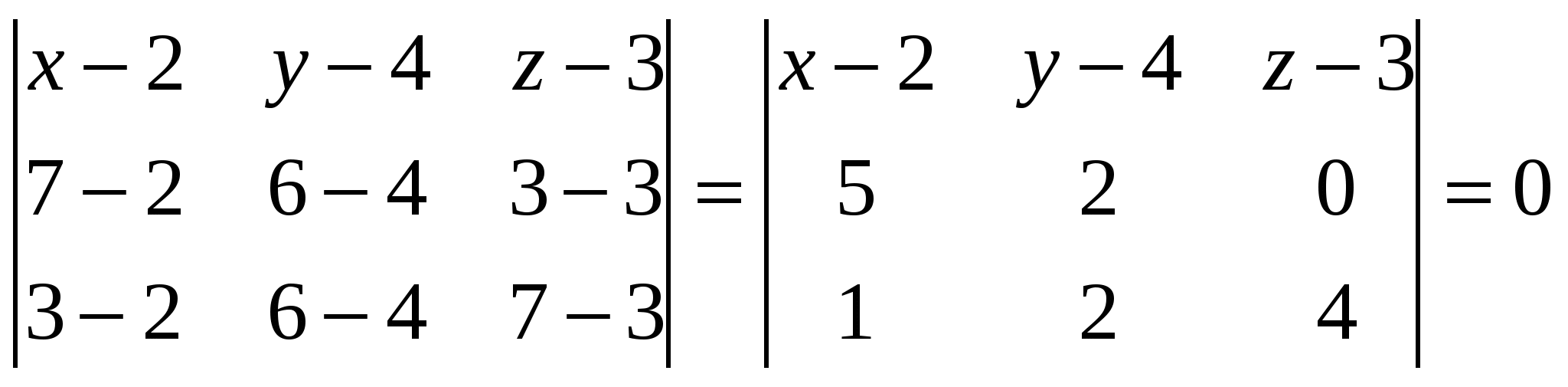







уравнение плоскости, проходящей через точки А₁, А₂, А₄:



Общие уравнения прямой А₁А₂: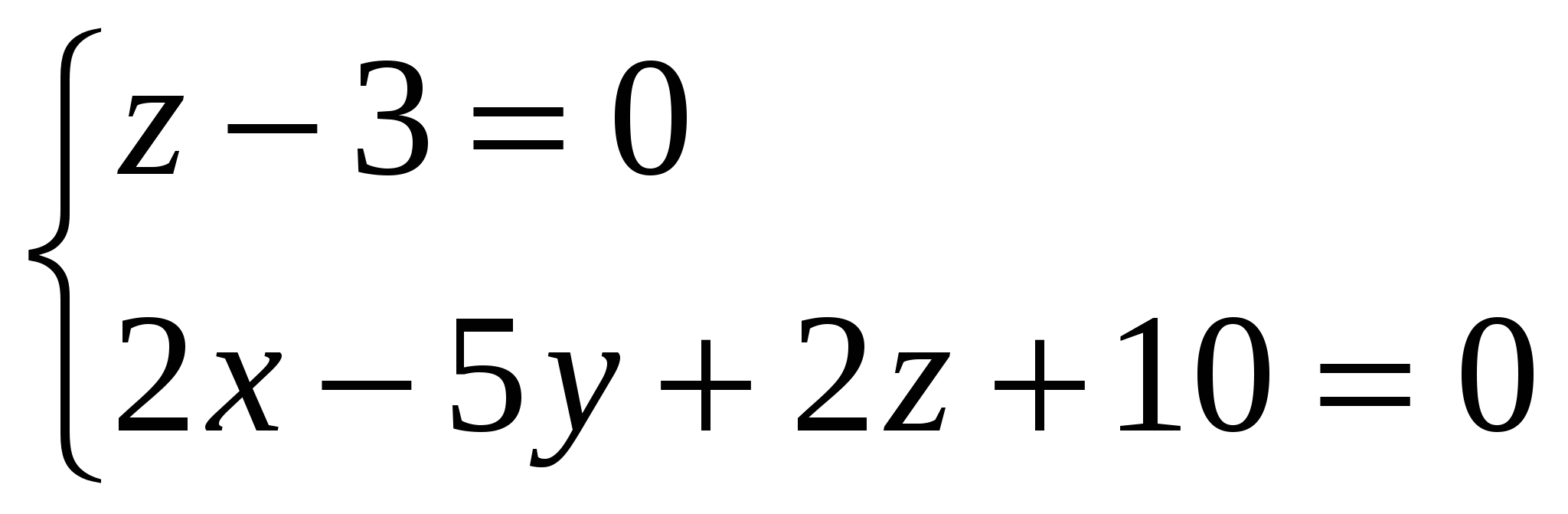


б). каноническое уравнение прямой А₁А₂:

,



– каноническое уравнение ребра А₁А₂
с). параметрическое уравнение прямой А₁А₂: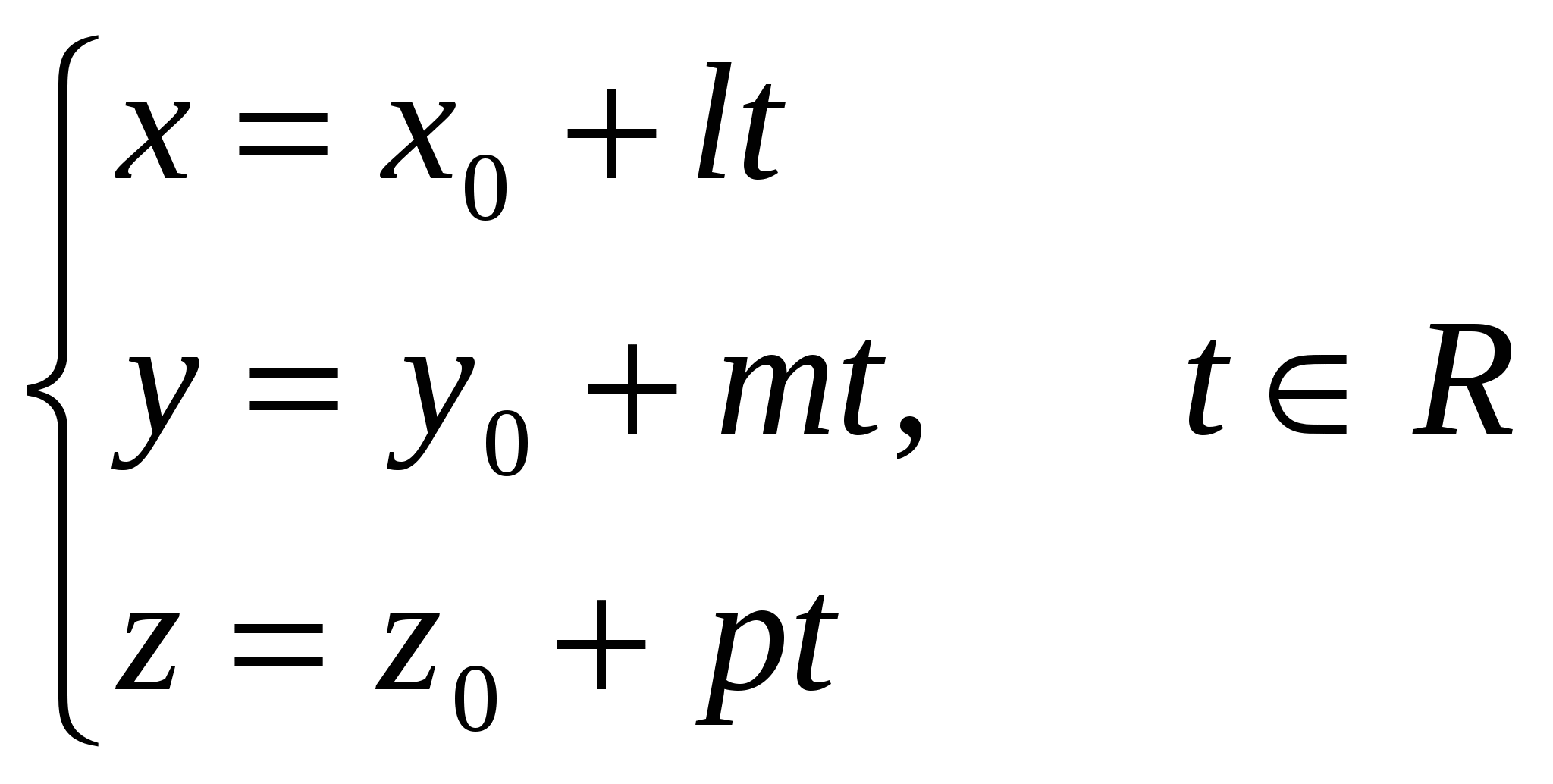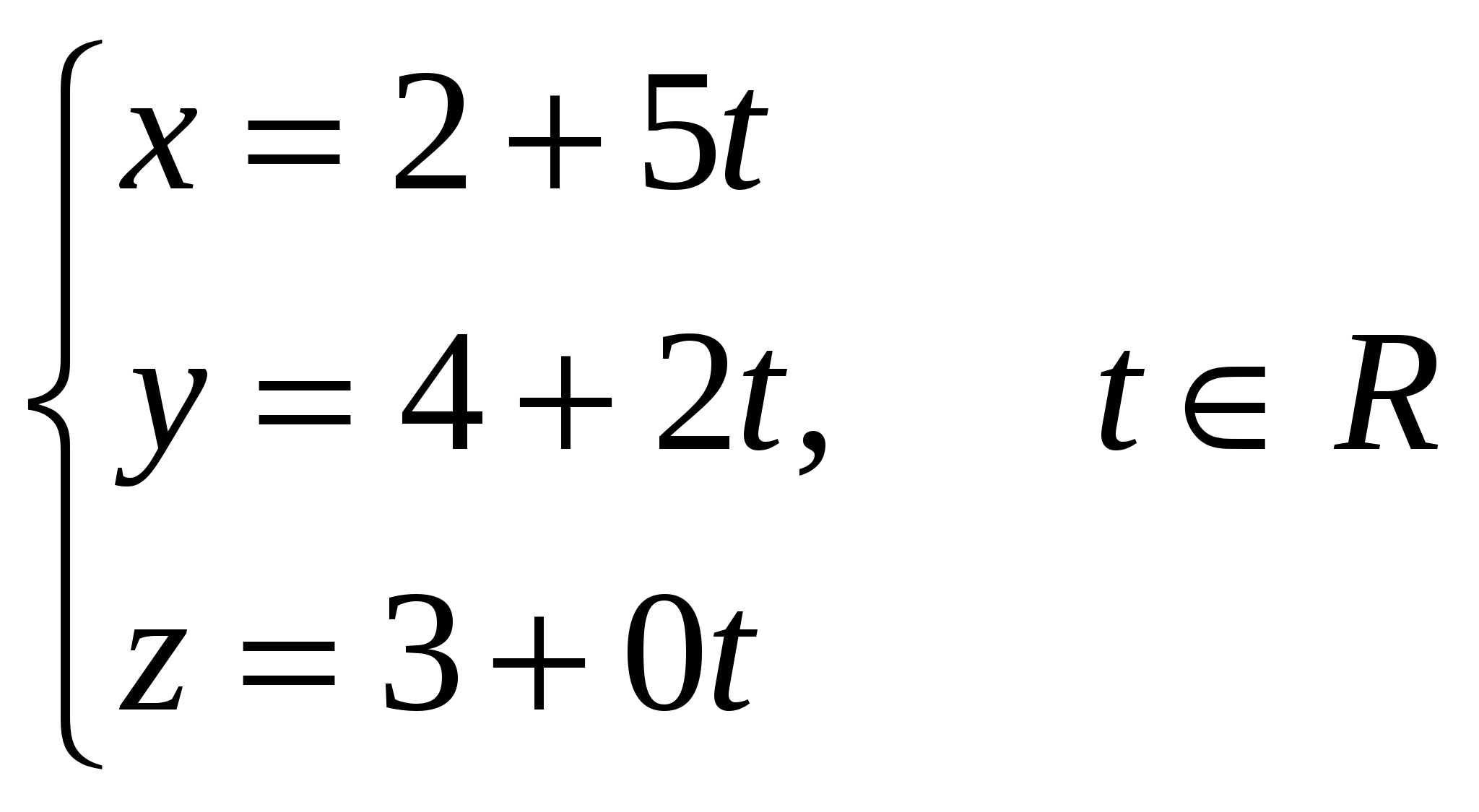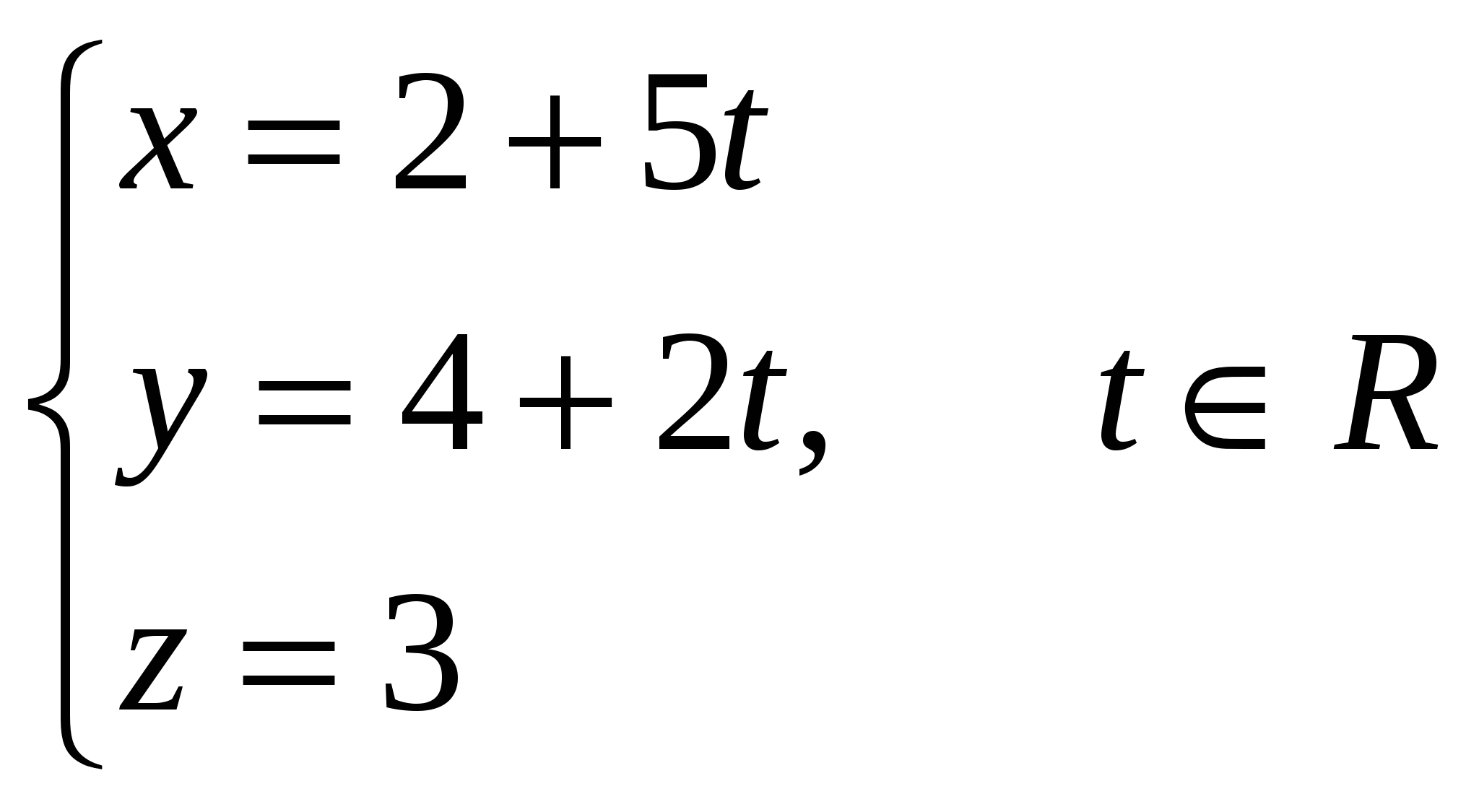







7) уравнение плоскости А₁А₂А₃;
А₁(2,4,3), А₂(7,6,3), А₃(4,9,3):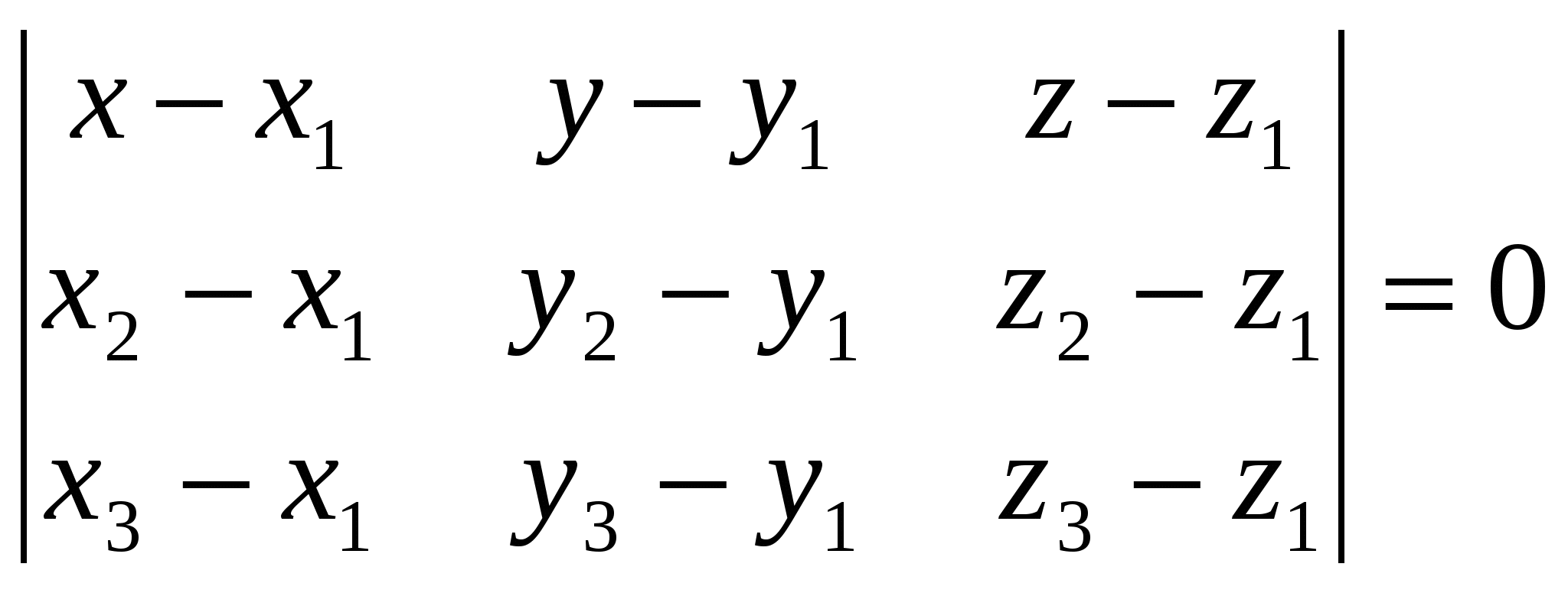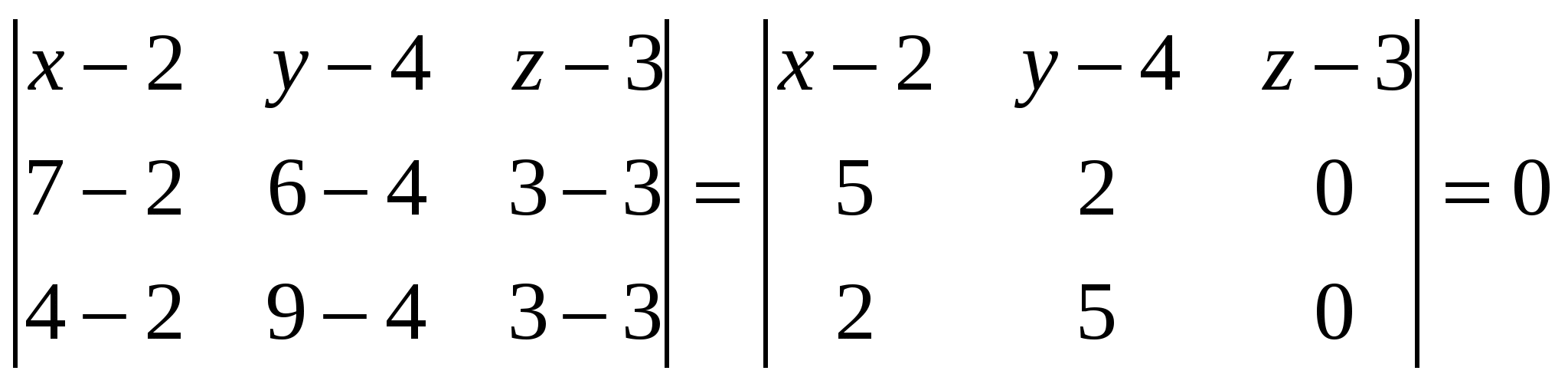





уравнение плоскости, проходящей через точки А₁, А₂, А₃:



8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

уравнение плоскости, проходящей через точки А₁, А₂, А₃:



Нормальный вектор данной плоскости



Уравнение высоты А₄Н, опущенной из т. А₄(3,6,7) на плоскость А₁А₂А₃, имеет вид:



Найдем координаты т.Н:

Решая параметрическое уравнение прямой А₄Н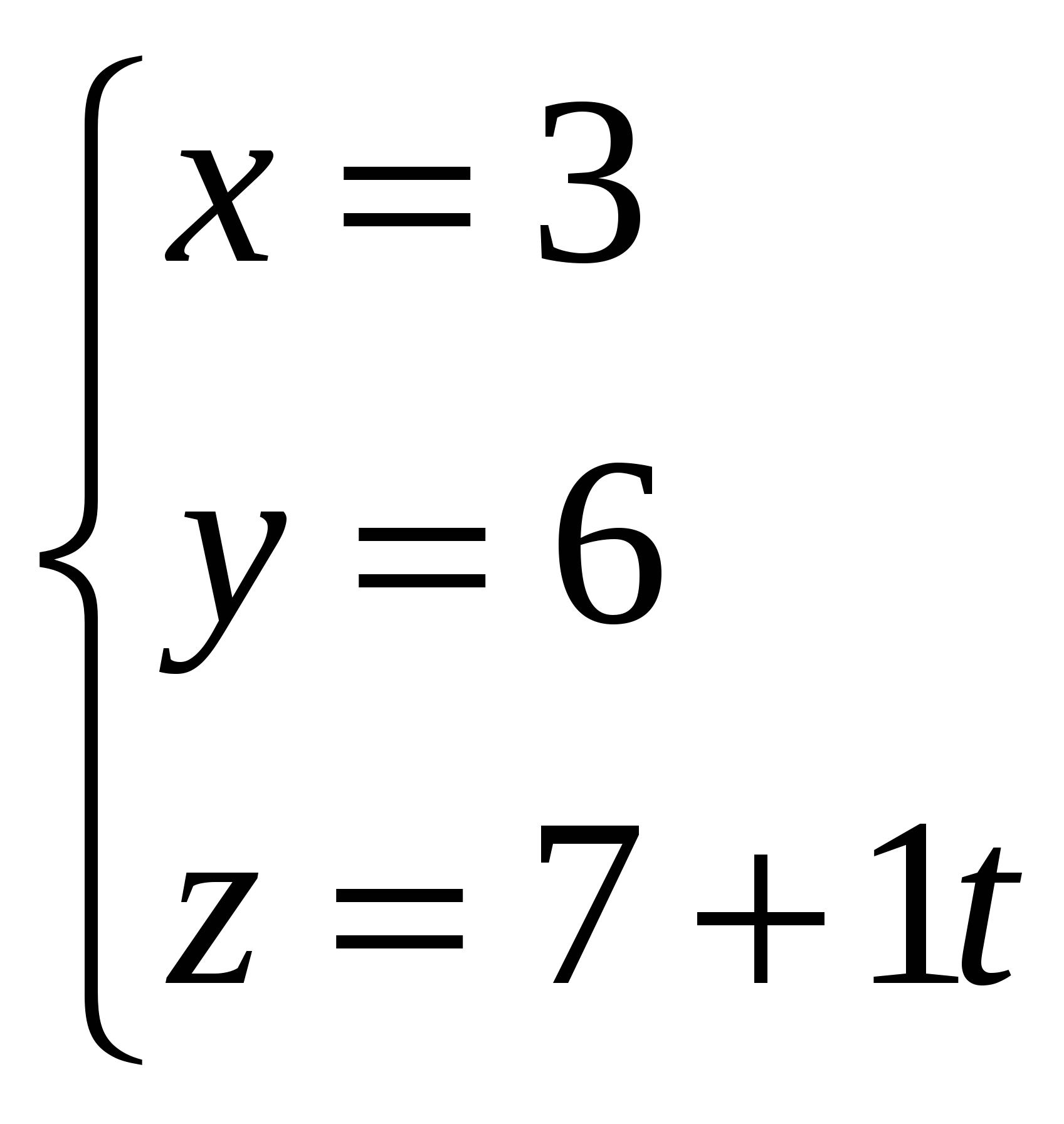

и уравнение плоскости А₁А₂А₃: 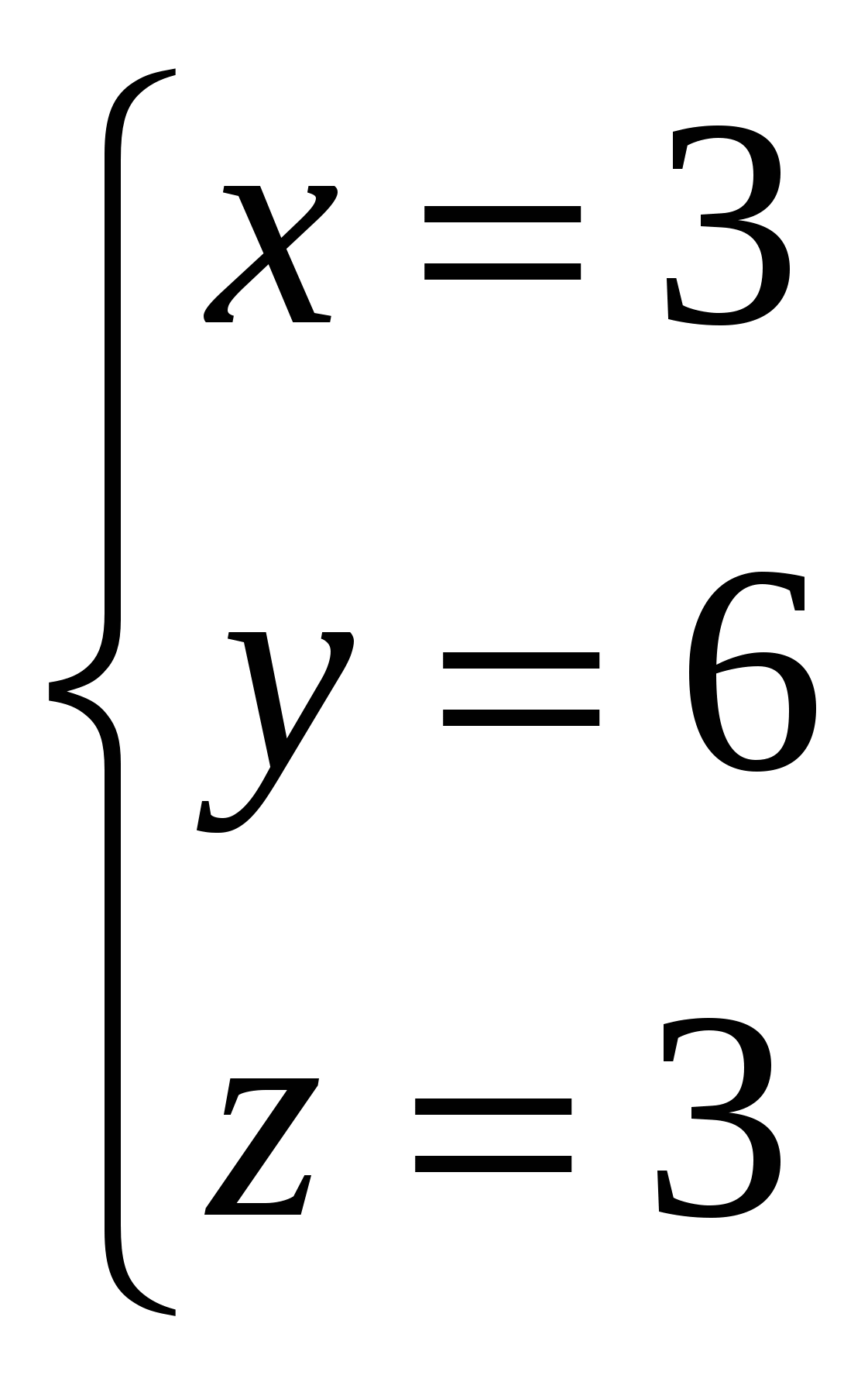, имеем: , отсюда координаты т.Н: