Все задачи. Решение Как известно, базисом в пространстве является любая упорядоченная система из трёх линейно независимых векторов. Покажем, что векторы, и линейно независимы, т е. выполняется равенство
 Скачать 1 Mb. Скачать 1 Mb.
|
|
Задача 24. Вычислить координаты центра окружности, описанной около треугольника с вершинами A(-1,1), B(2,-1), C(4,0). Решение: Центр описанной окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника. Найдем уравнения прямых, на которых лежат стороны треугольника и их угловые коэффициенты: АВ: ВС: АС: Координаты середин сторон: Угловые коэффициенты перпендикулярных прямых имеют обратную пропорциональность: Уравнения серединных высот: DO: EO: FO: 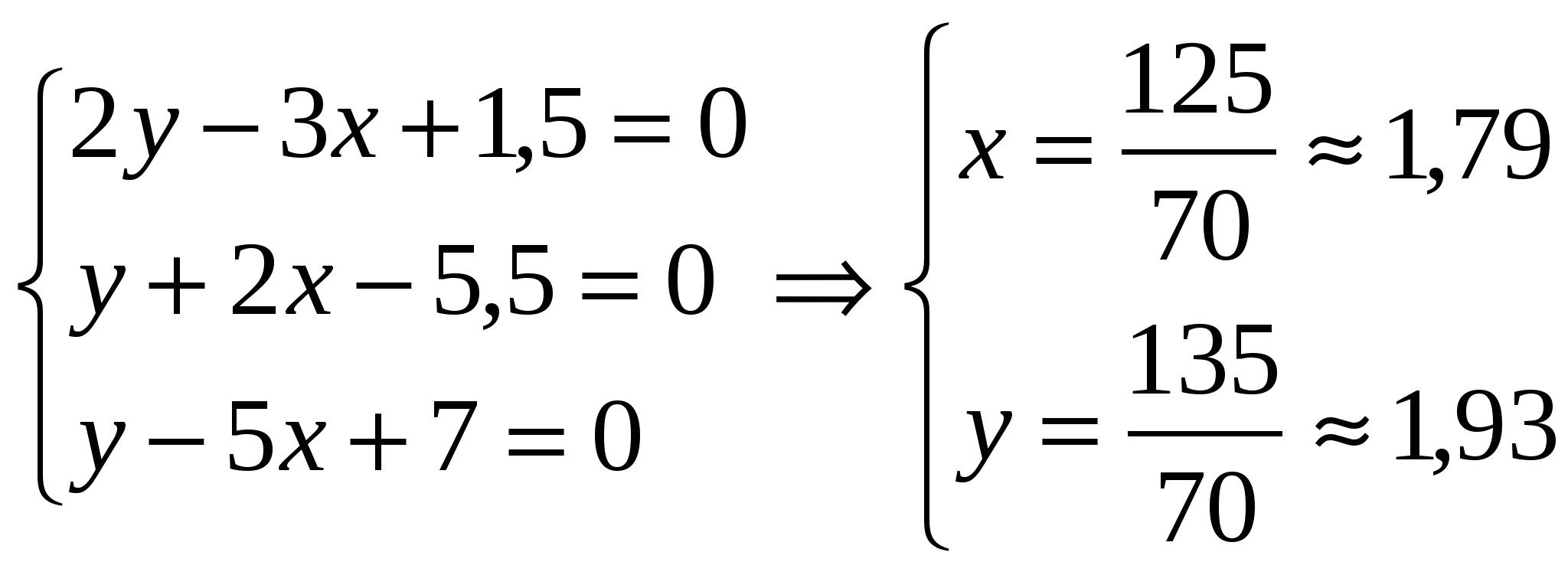  Задача 34. Построить на плоскости область решений системы линейных неравенств. 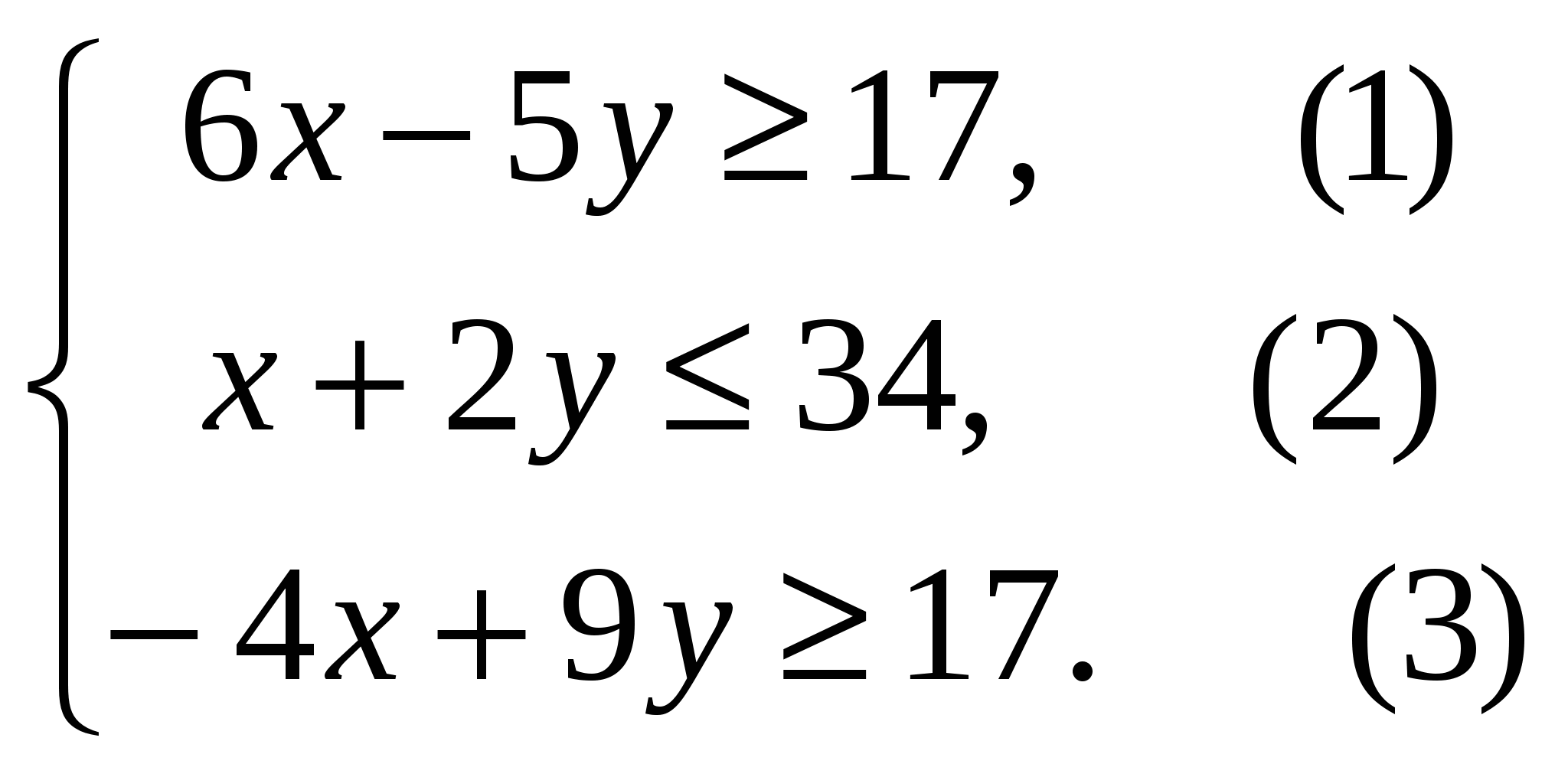 Решение: Строим область решений системы. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (см. рис.) строим прямую  Найдем теоретически точки пересечений прямых: 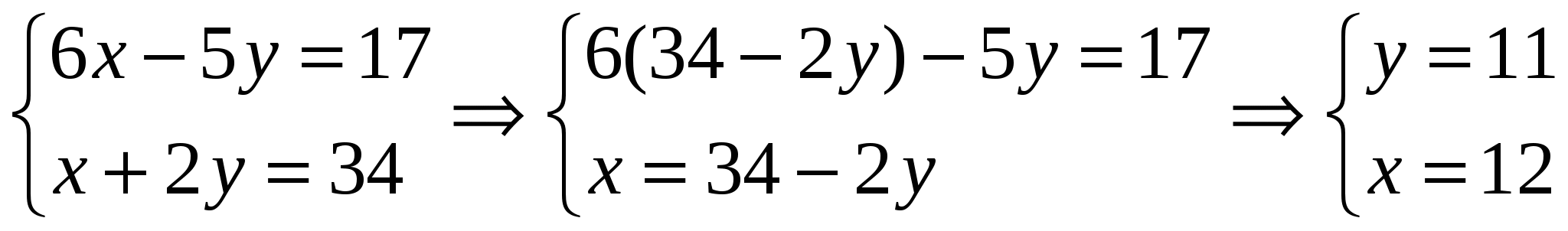 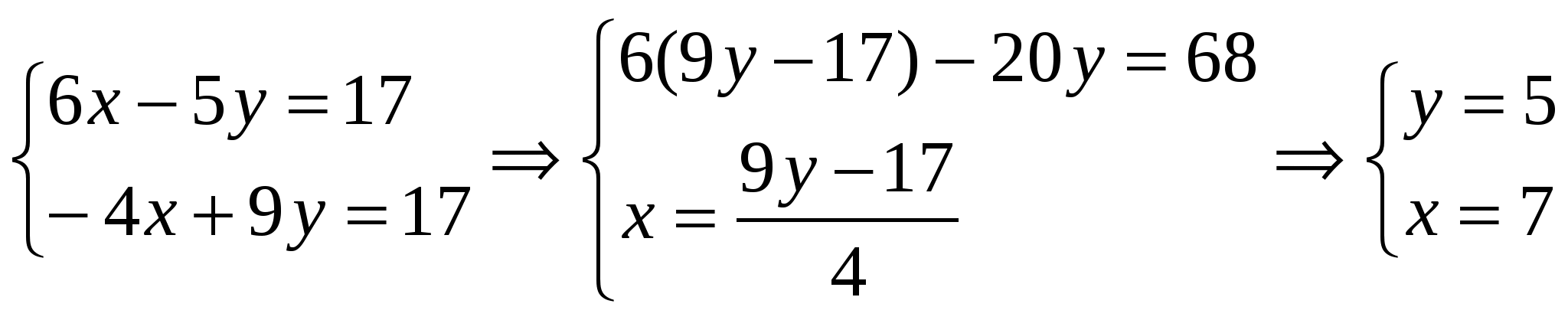 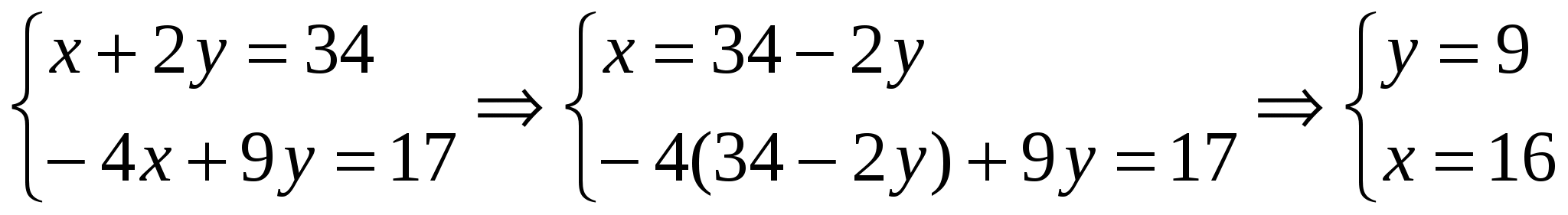 Задача 44. Составить уравнение линии, каждая точка которой находится вдвое ближе к точке A(1,0), чем к точке B(-2,0). Решение: Каждая точка с другой стороны, она должна также удовлетворять условию следовательно, искомая прямая есть решение системы 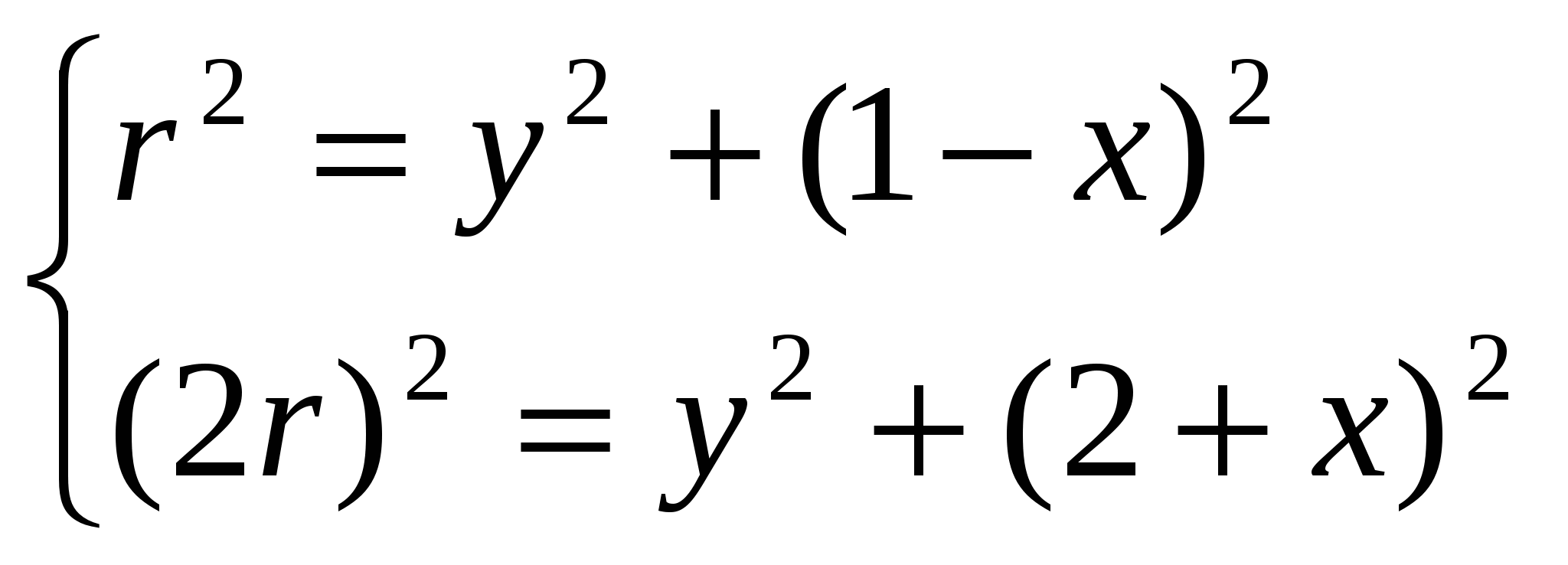 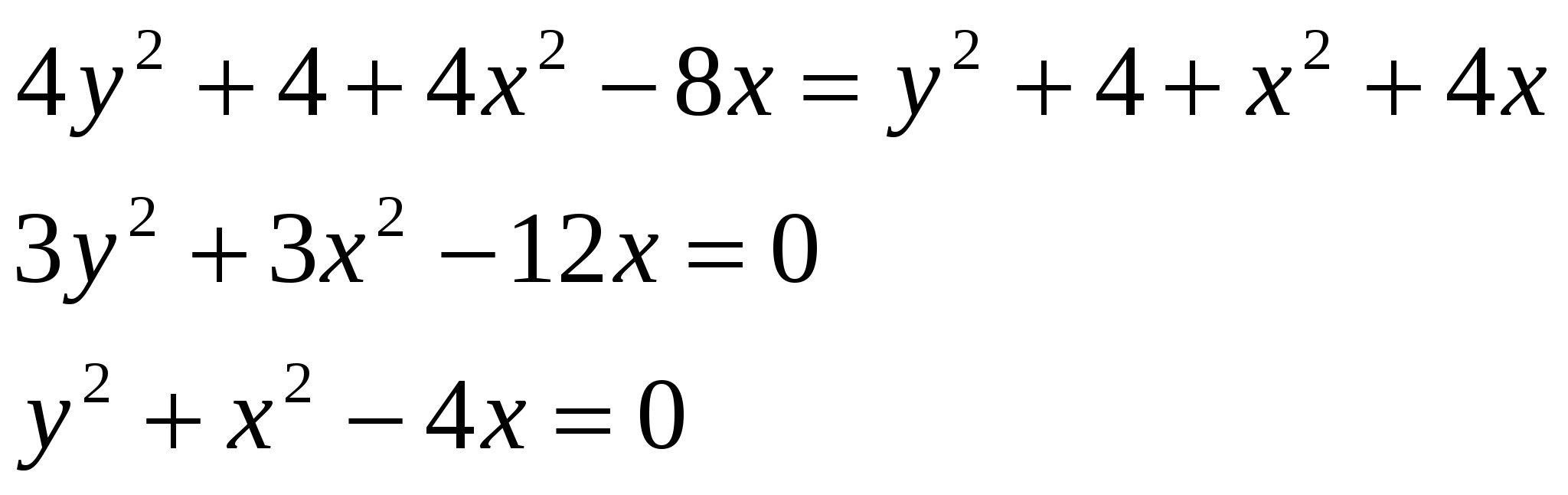  Задача 54. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления. 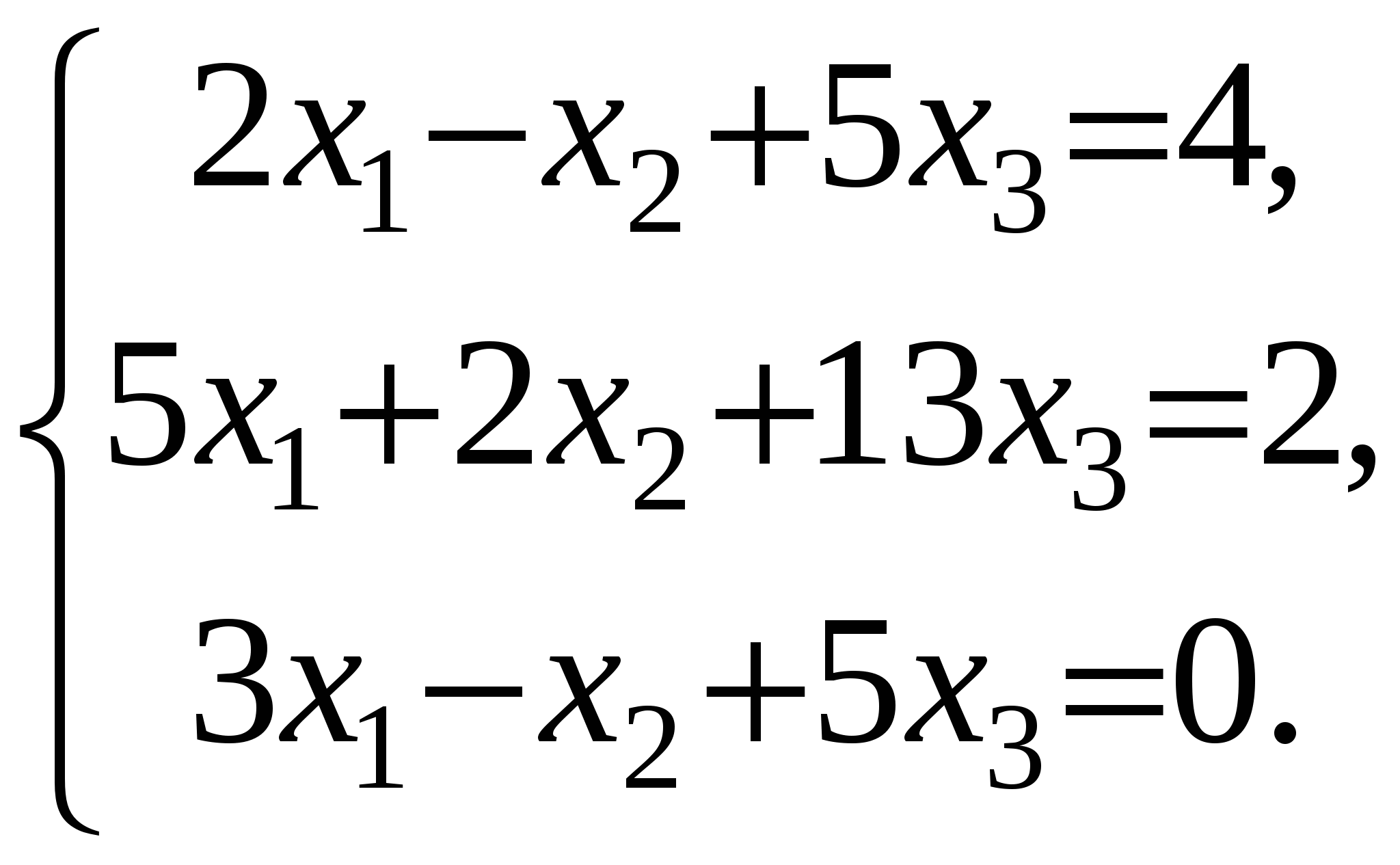 Решение: Запишем матрицу коэффициентов системы А и расширенную матрицу системы В: 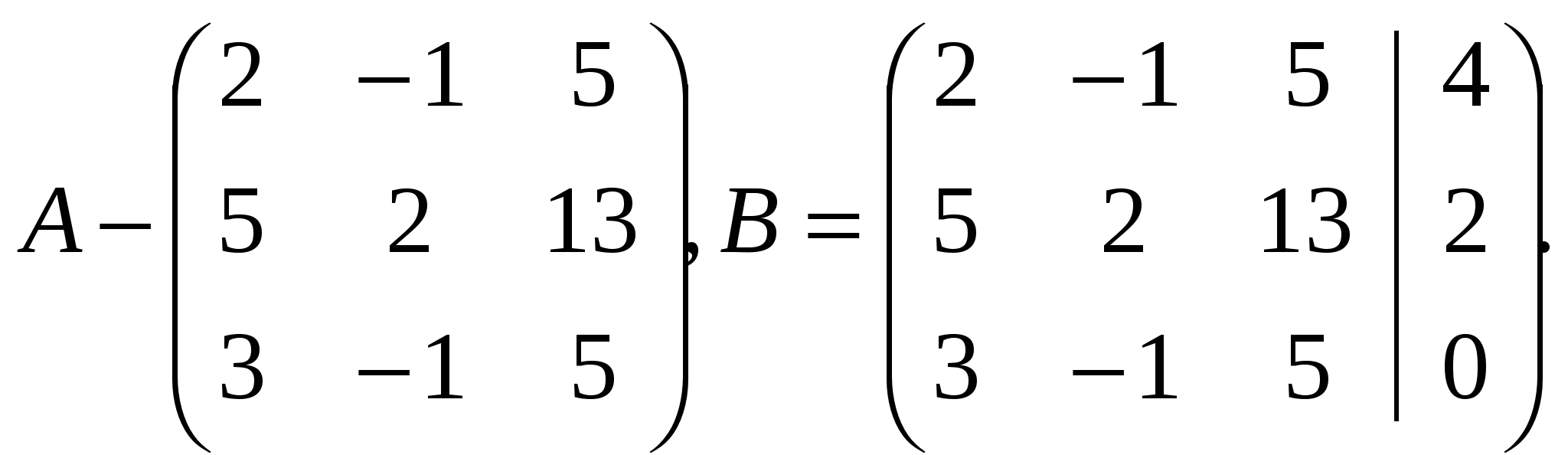 Вертикальной чертой мы отделили элементы матрицы системы от свободных членов системы. Определим ранги матрицы А и В. Для этого проведём преобразования матрицы В:
Третью строку сложим с первой строкой, умноженной на (-3);
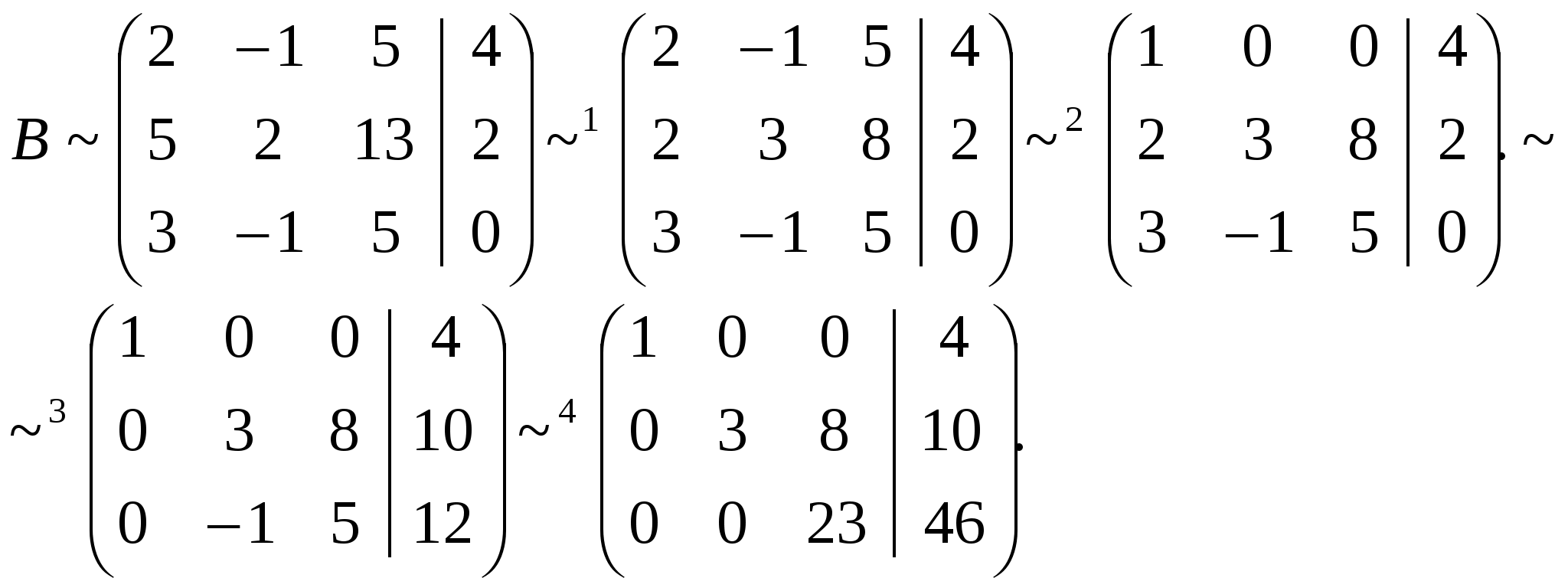 Отсюда следует, что r(В)=3, минор третьего порядка матрицы А 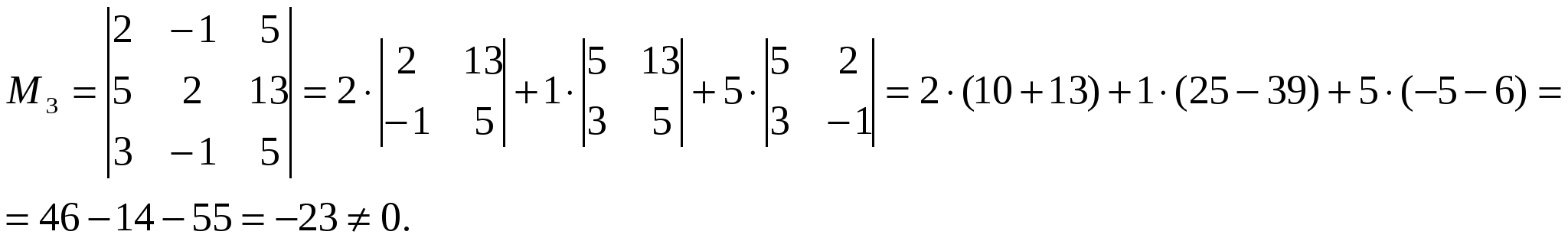 Следовательно, r(B) = r(A) = 3, т.е. данная система совместна. Но последняя преобразованная матрица В 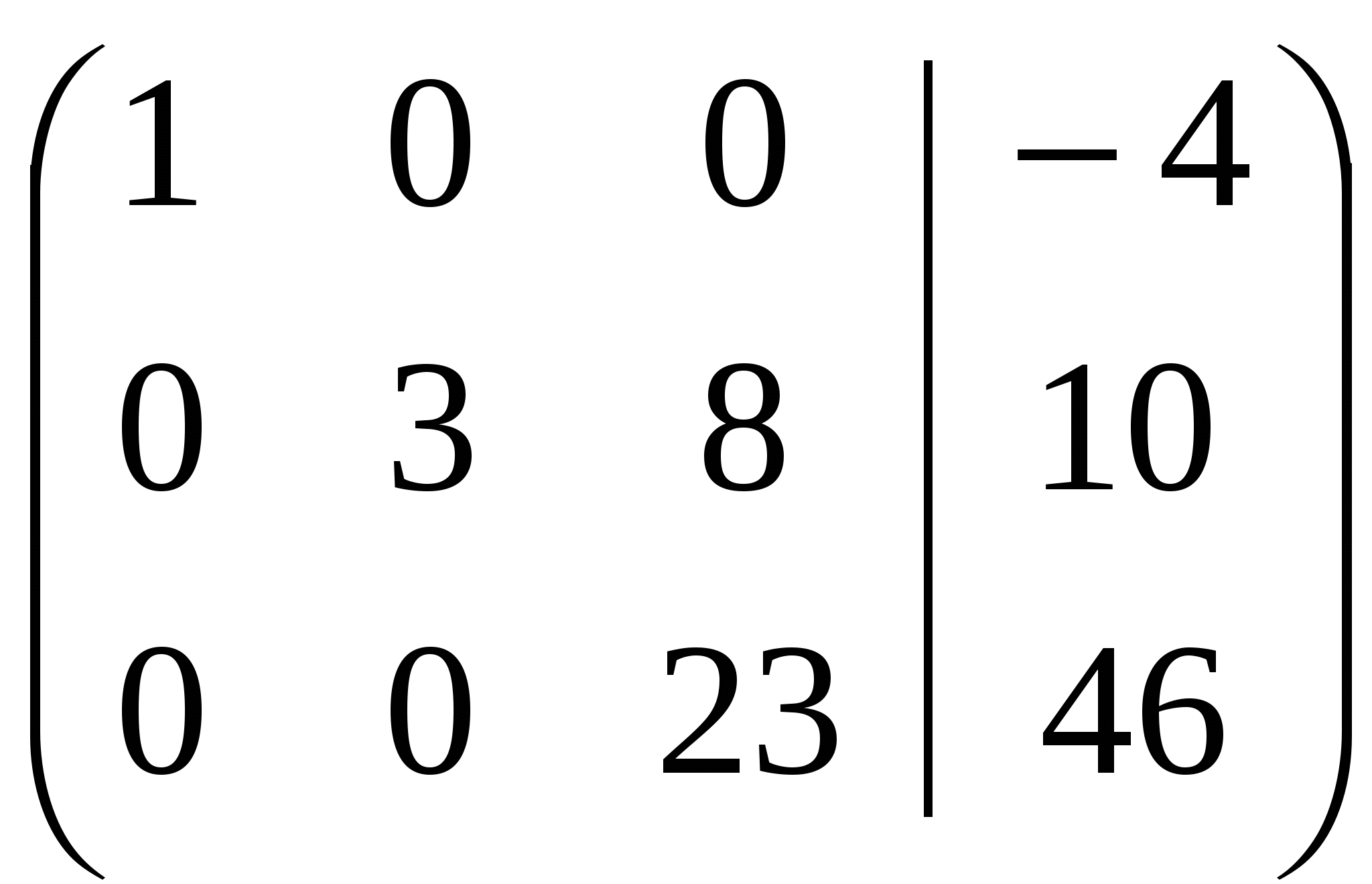 - это расширенная матрица системы - это расширенная матрица системы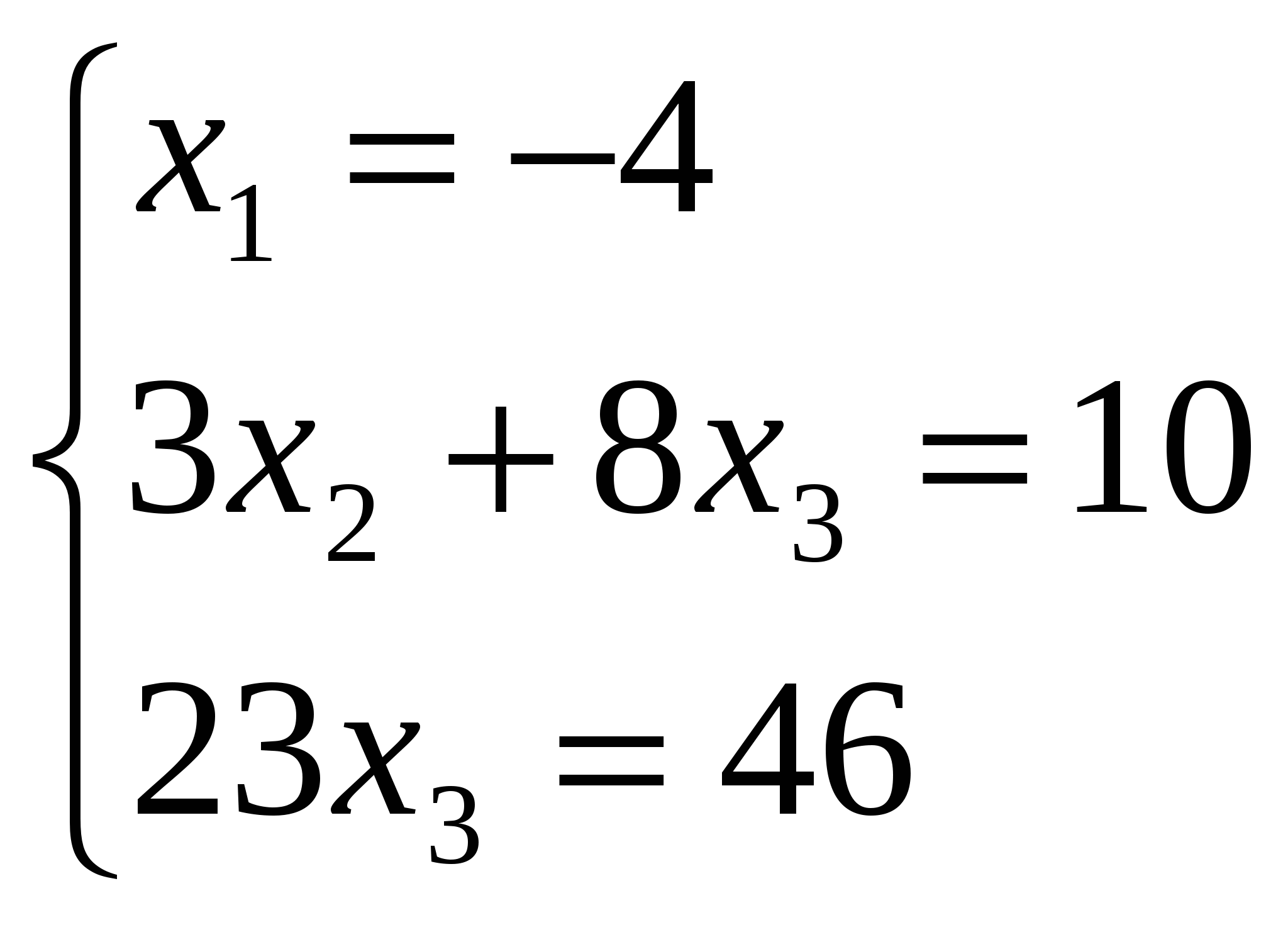 "Обратным ходом" метода Гаусса из последнего уравнения системы находим х3 = 2; из второго х2 = – 2; из первого х1 = – 4 Ответ: 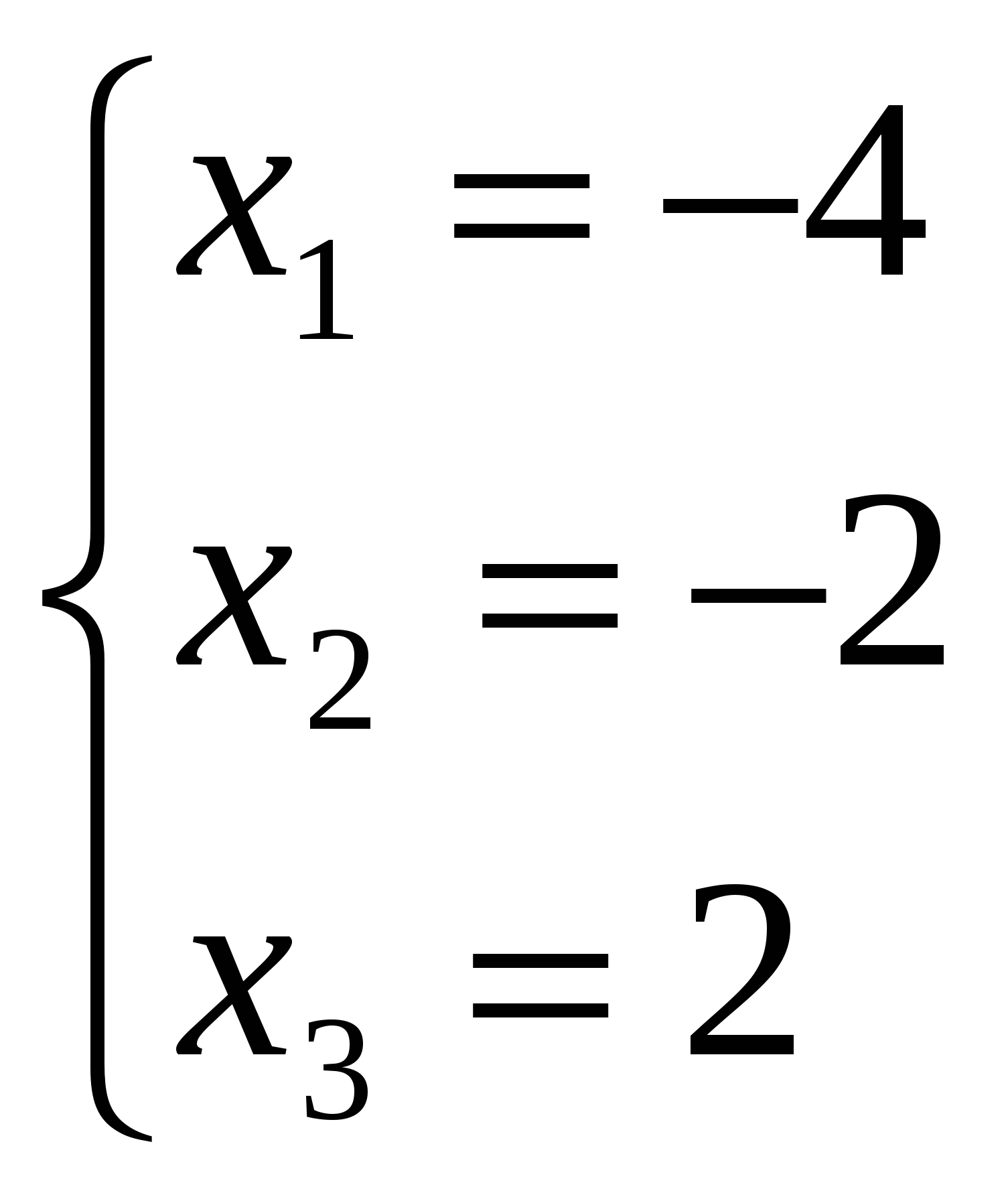 2) Решение матричным методом: Прежде всего, найдем матрицу А-1, обратную матрице А. Определитель основной матрицы системы: 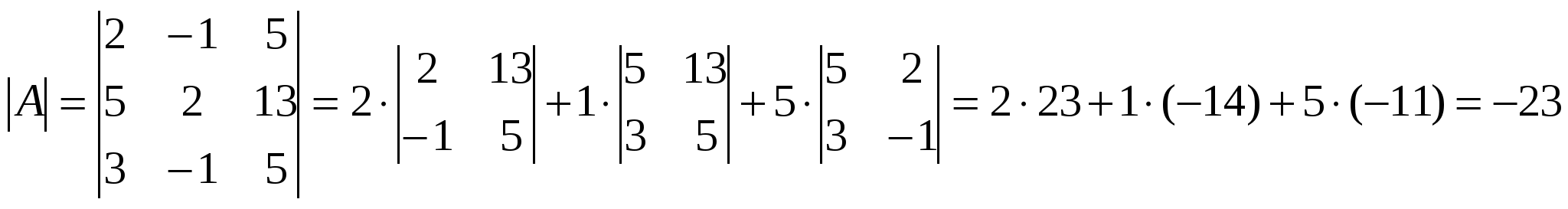 . .Алгебраические дополнения всех элементов: 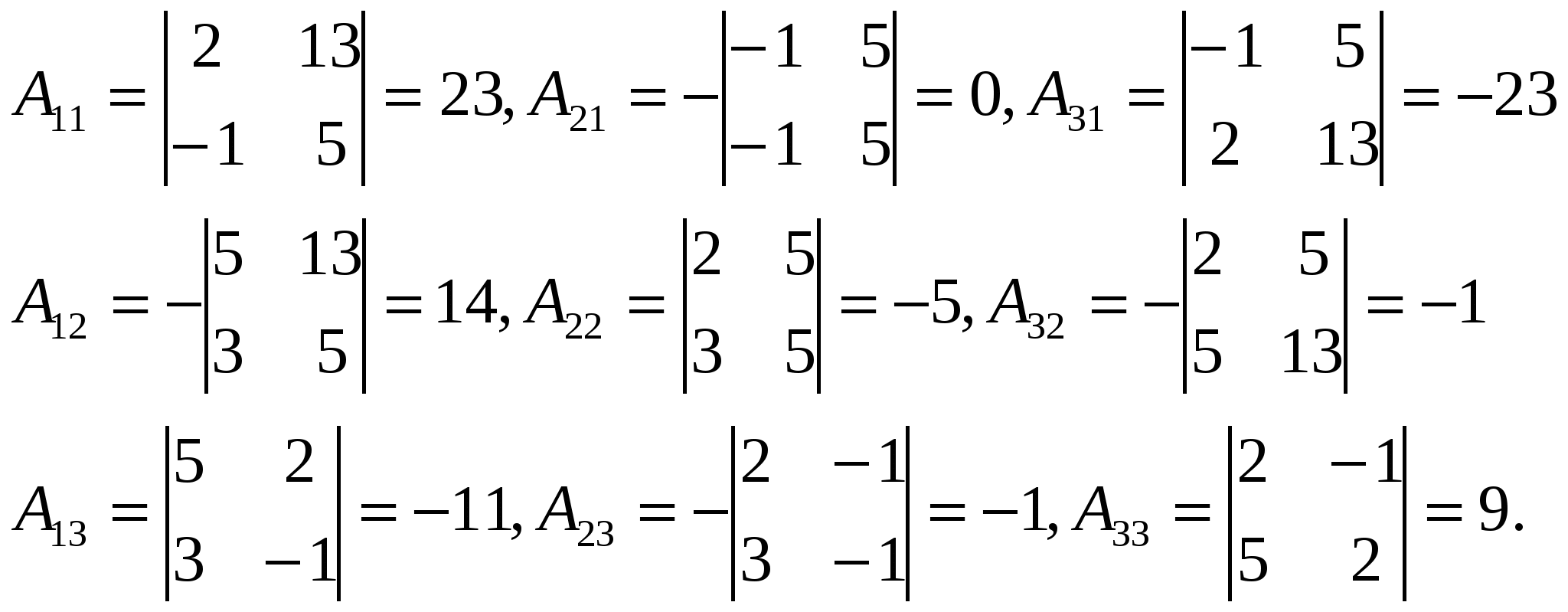 Отсюда 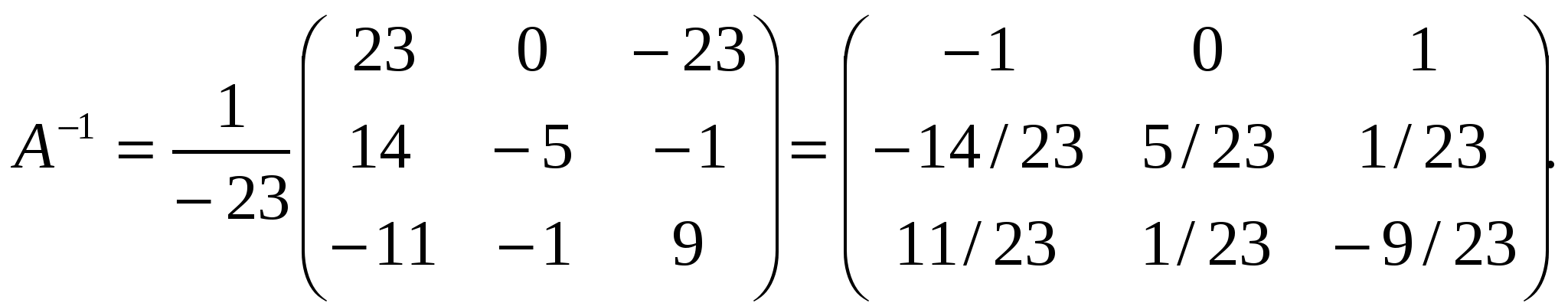 Тогда Х = 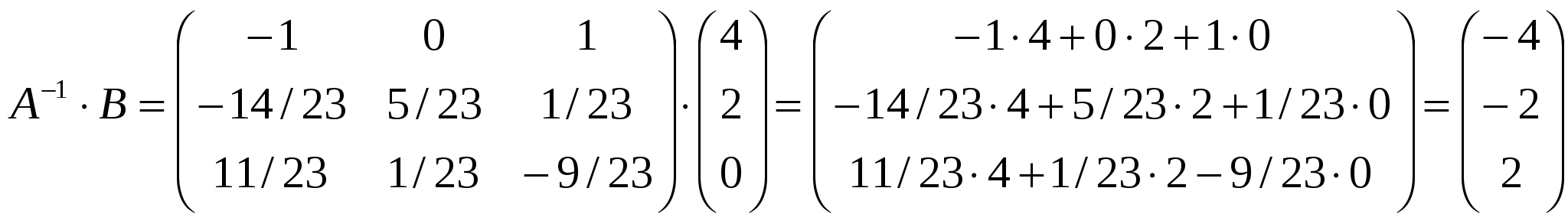 , ,и, следовательно х1=-4; х2=-2; х3=2. Задача 64. Найти размерность и базис пространства решений однородной системы линейных уравнений 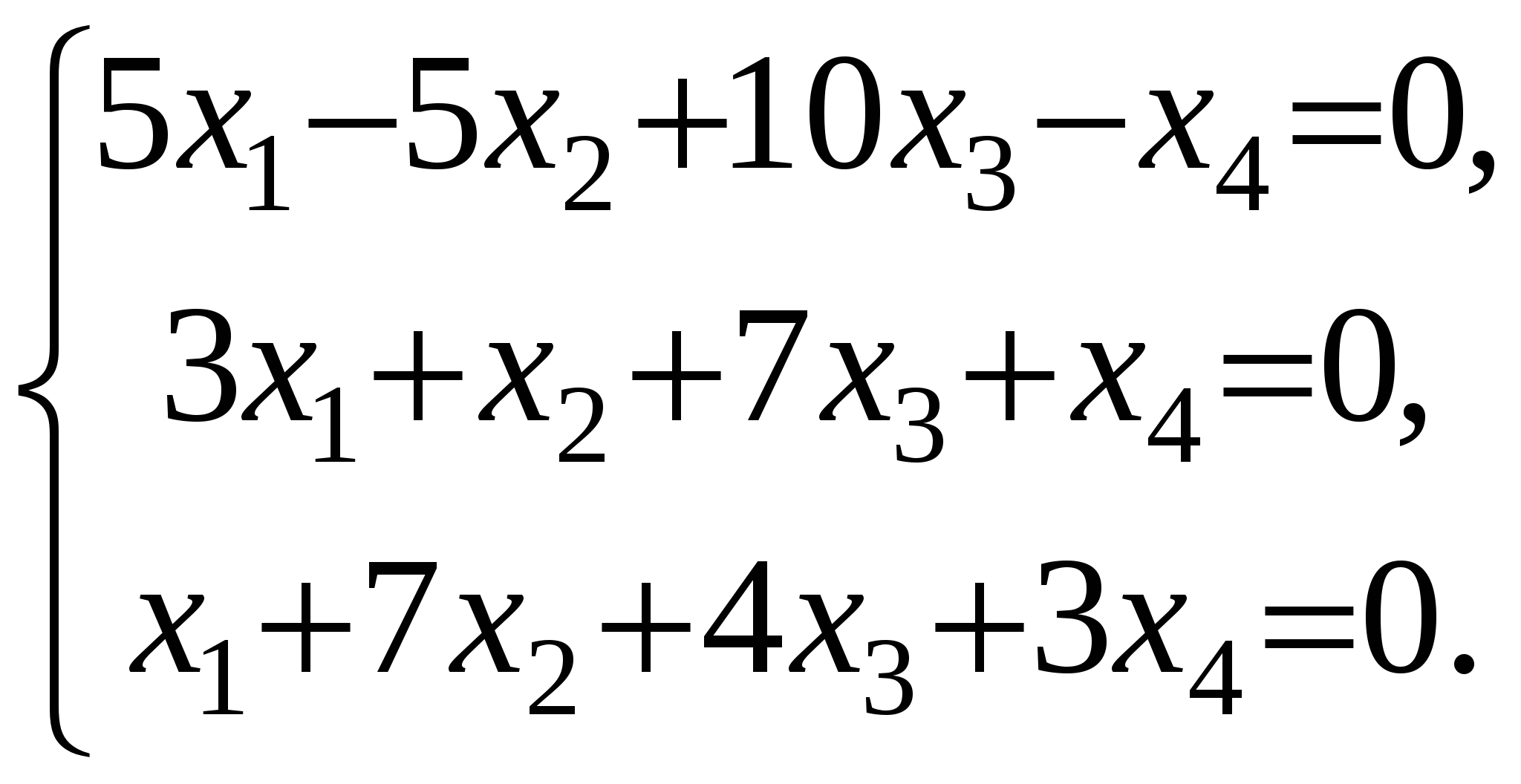 Решение: Данная система имеет размер 2×3. Она однородна, т.к. свободный член в каждом уравнении равен нулю. Число уравнений меньше числа неизвестных. Следовательно, множество решений системы бесконечно. 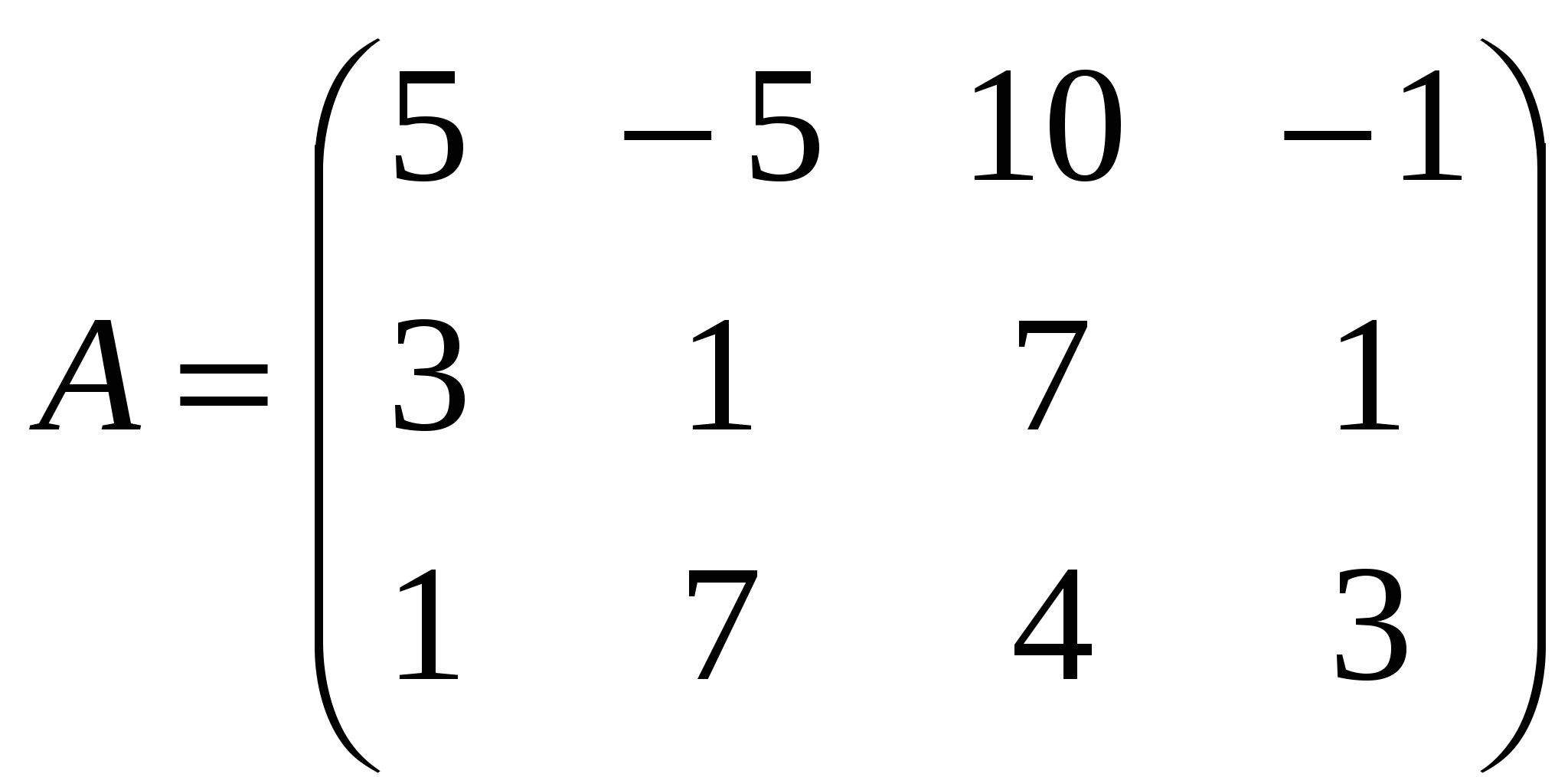 Проведем преобразования: Проведем преобразования: Для этого проведём преобразования матрицы А:
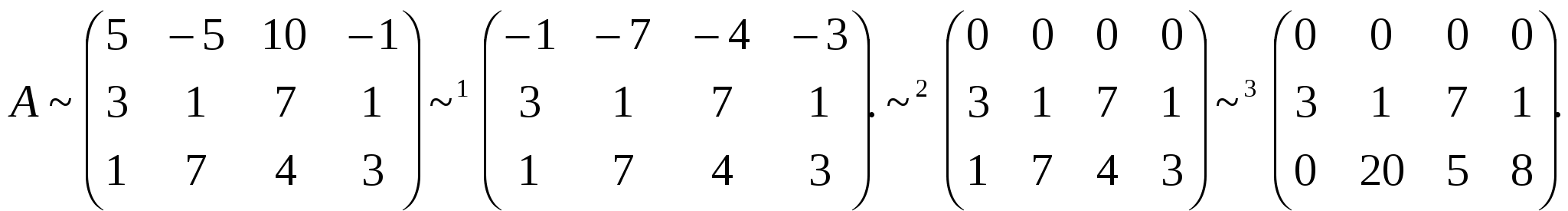 Ранг матрицы системы равен двум, так как только среди ее миноров второго порядка есть отличный от нуля, например минор Следовательно, данная система эквивалентна системе 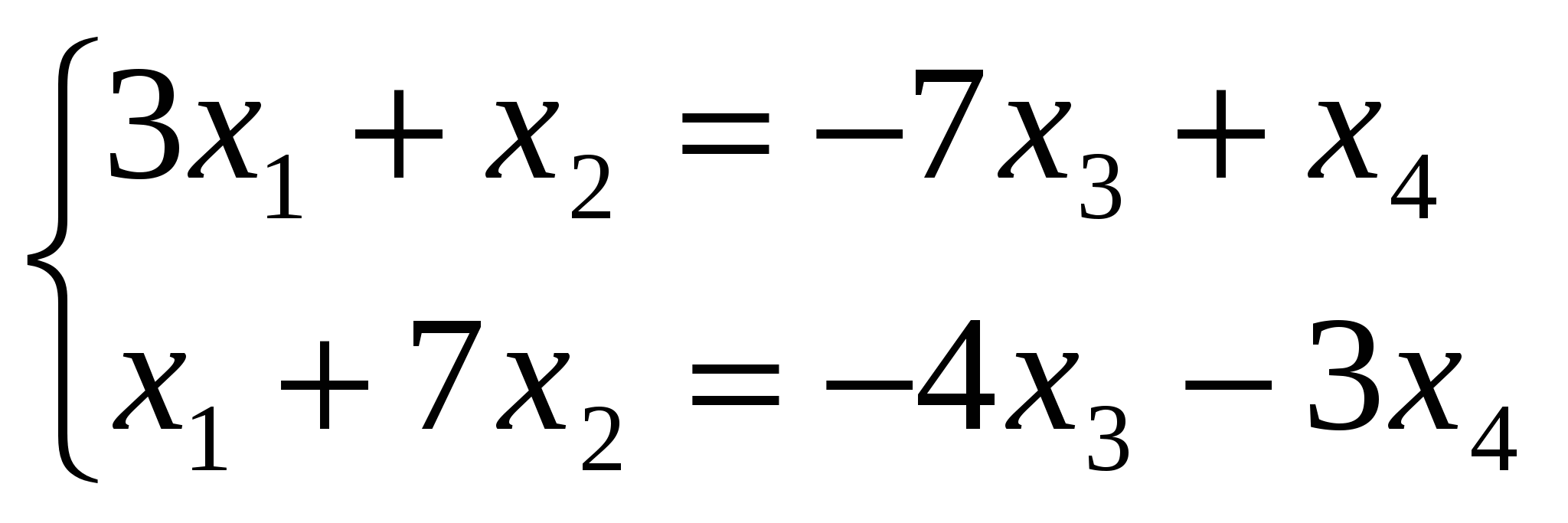 , , Отсюда 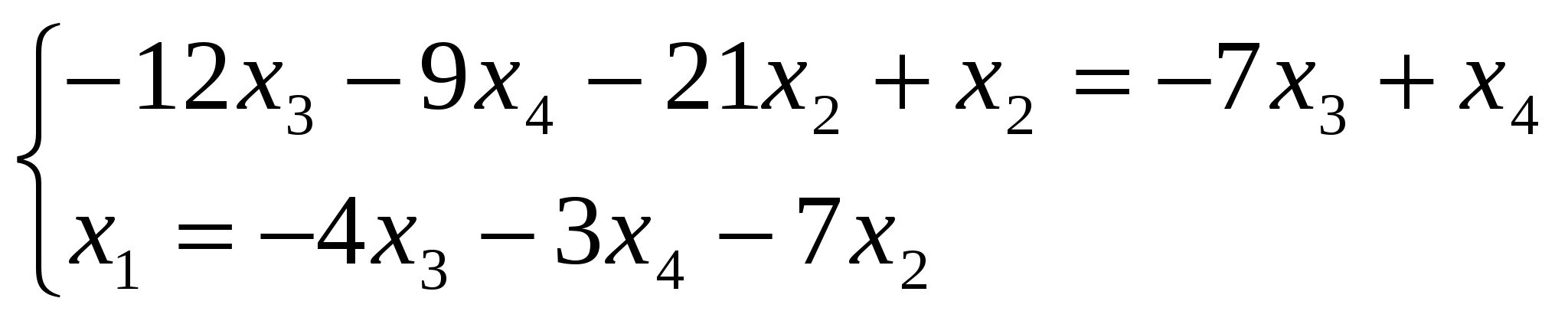 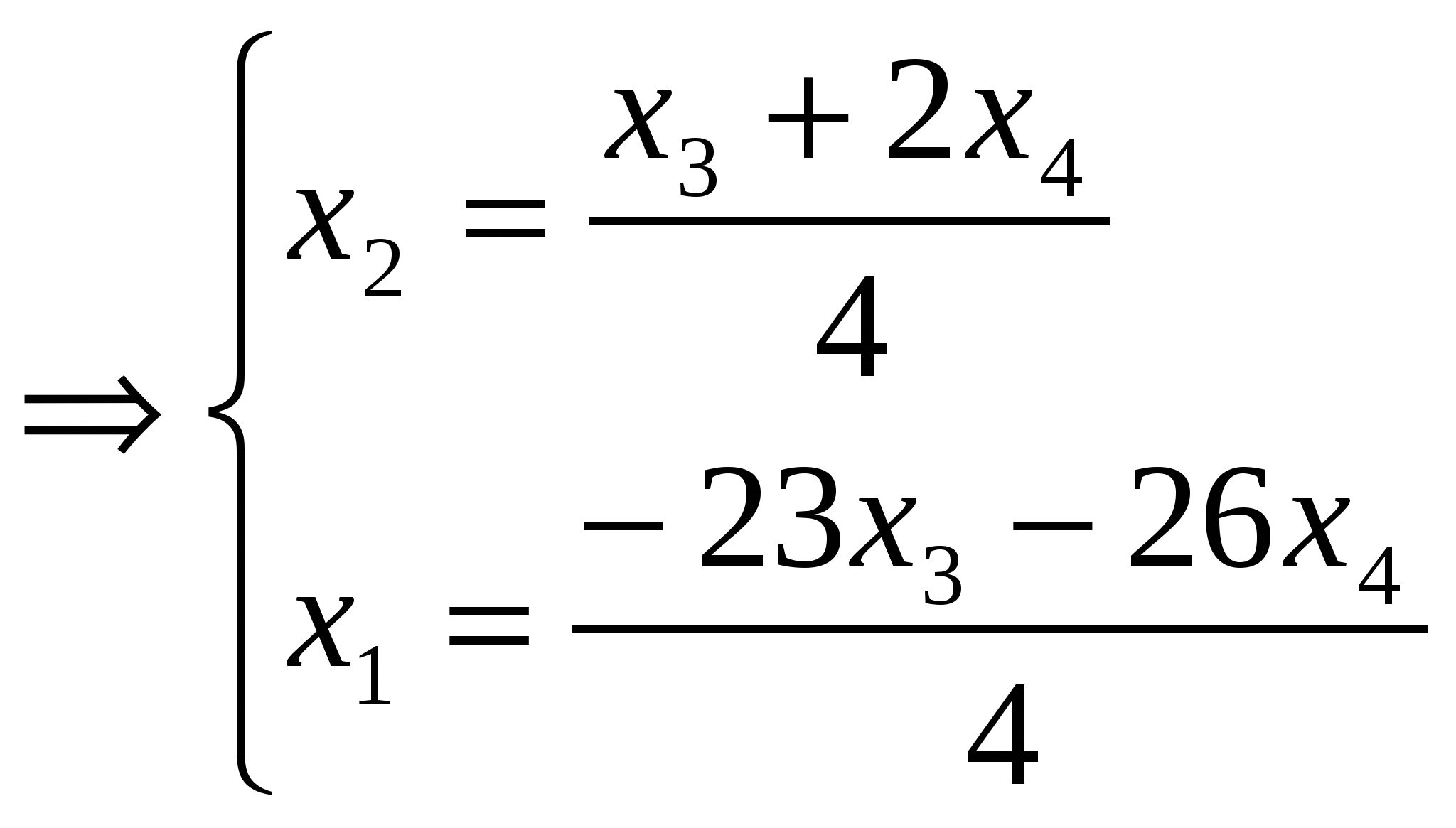 Следовательно, множество решений системы имеет вид Задача 74. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее 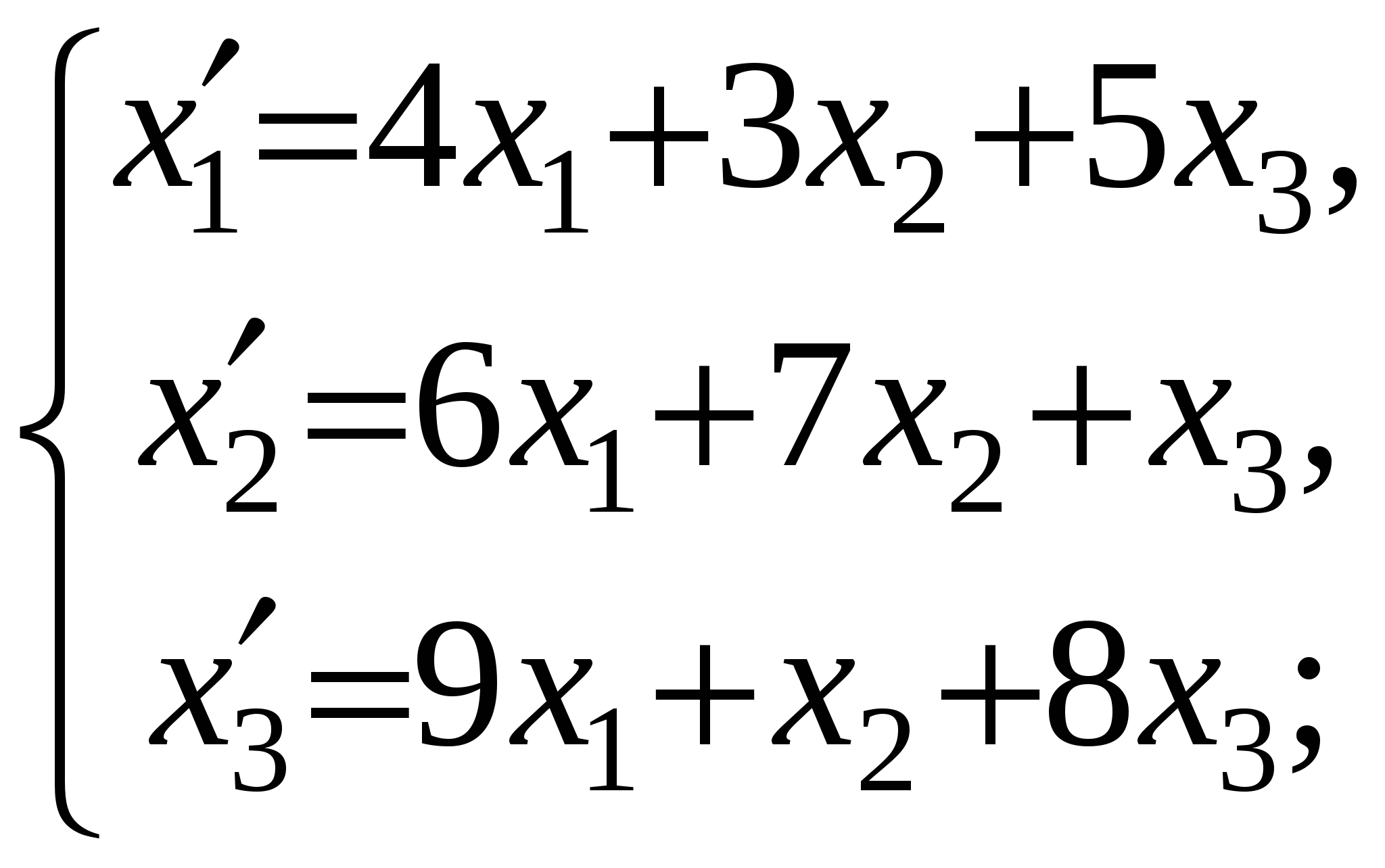 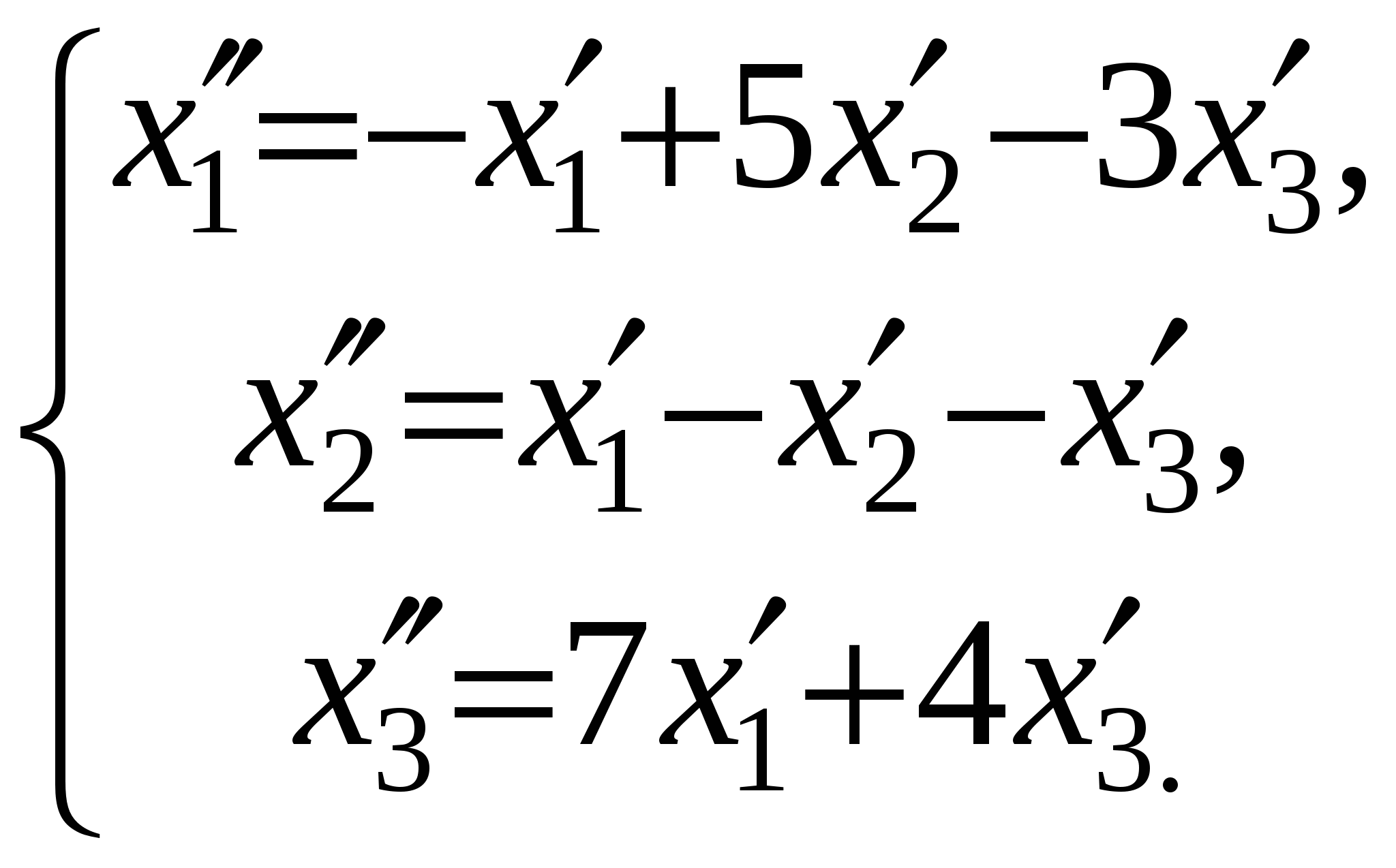 Решение: Составим две матрицы: 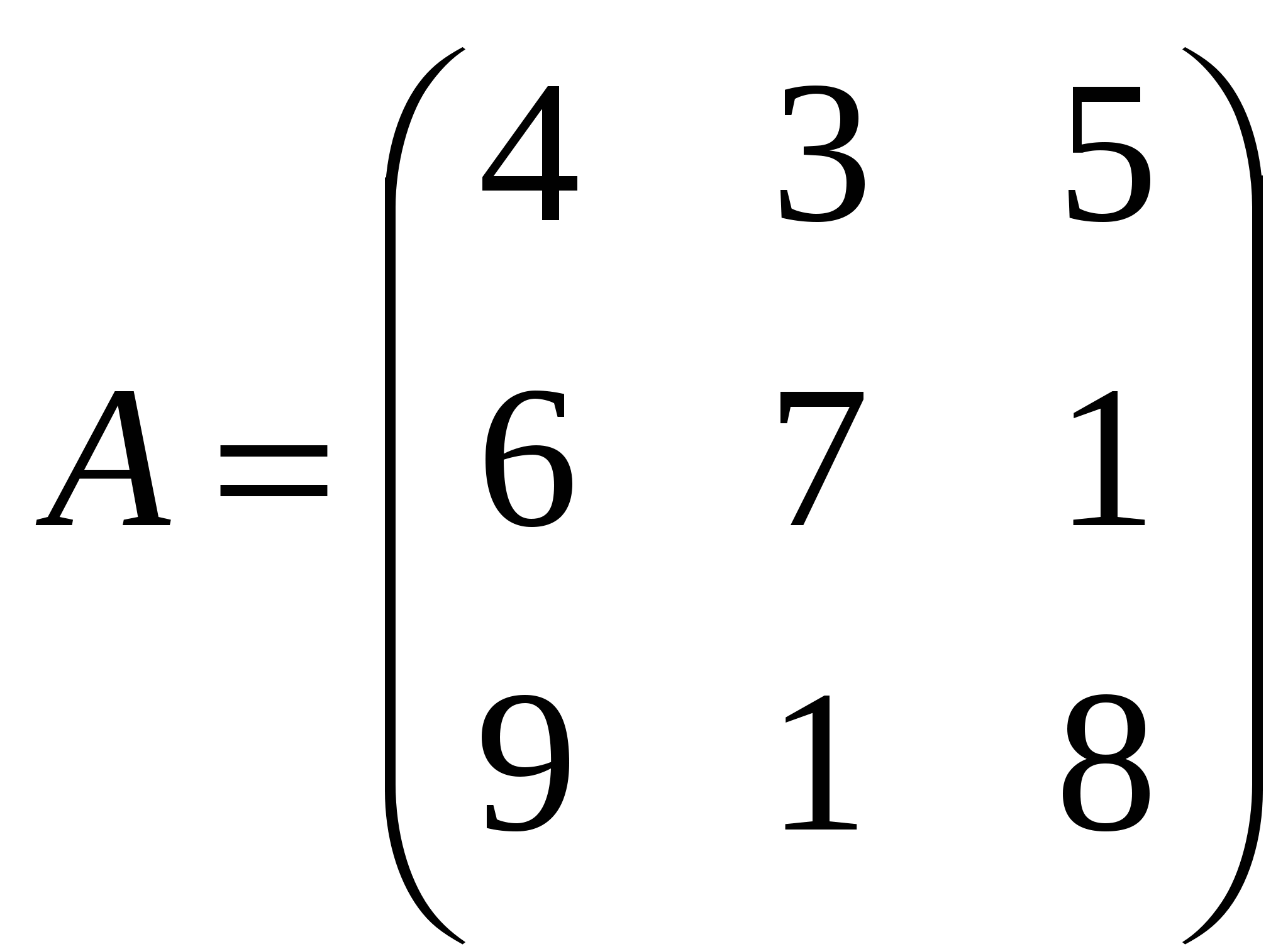 и и 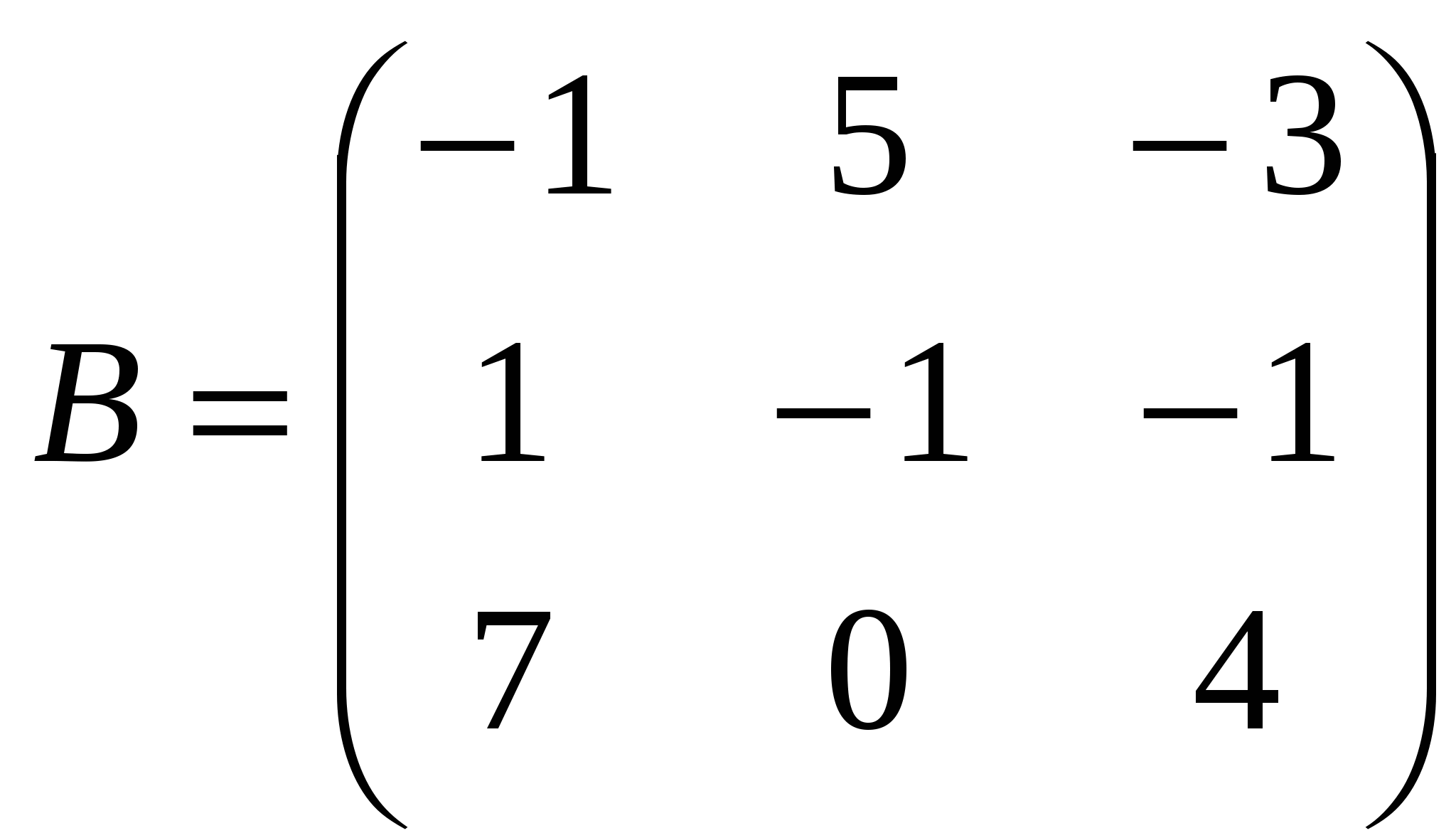 найдем их произведение: 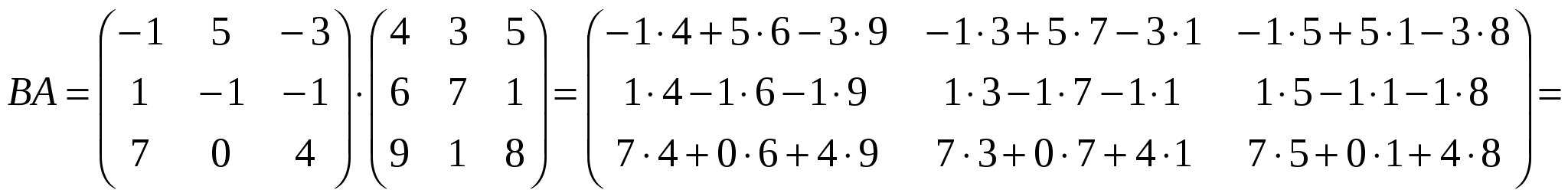 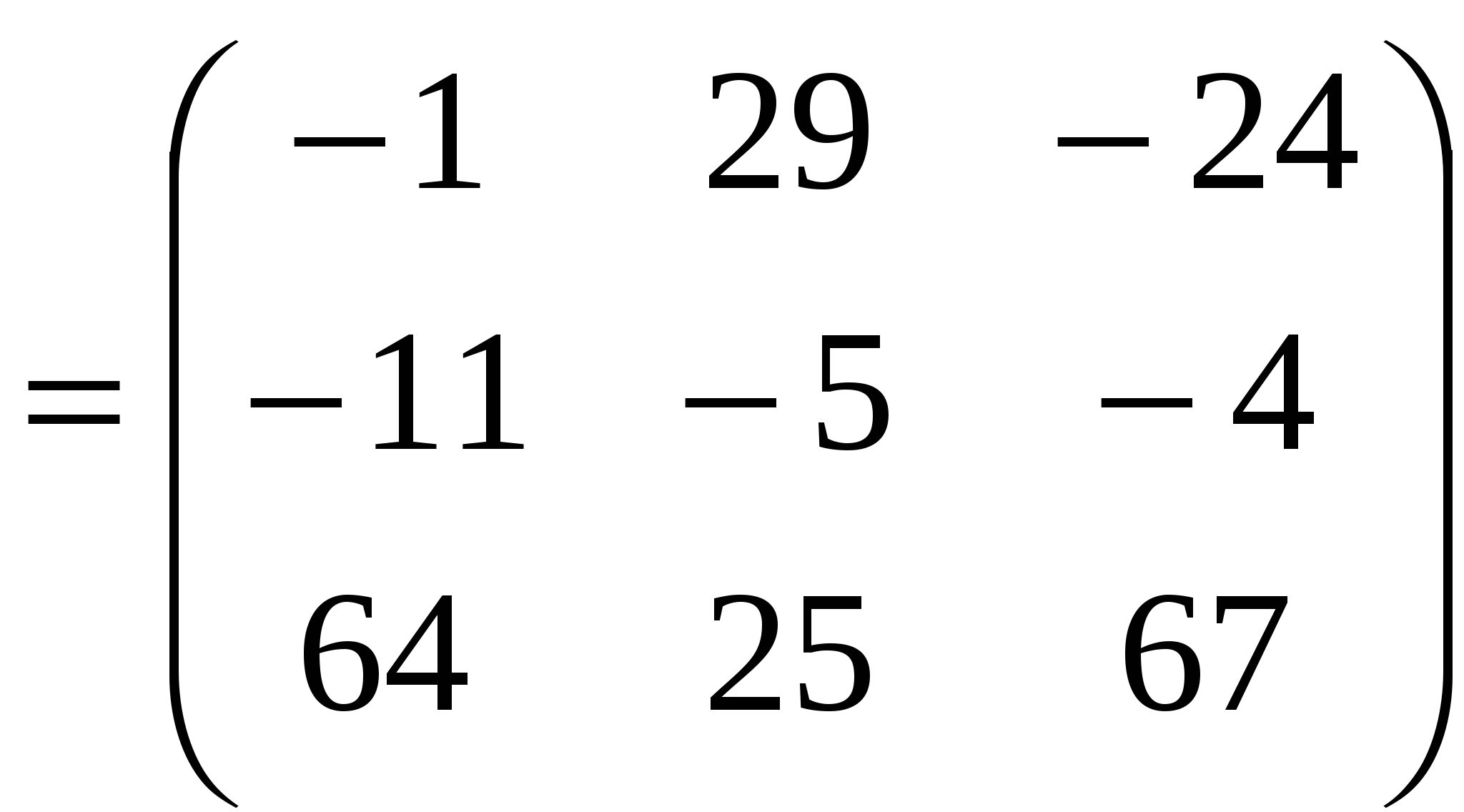 Поэтому искомое линейное преобразование имеет вид: 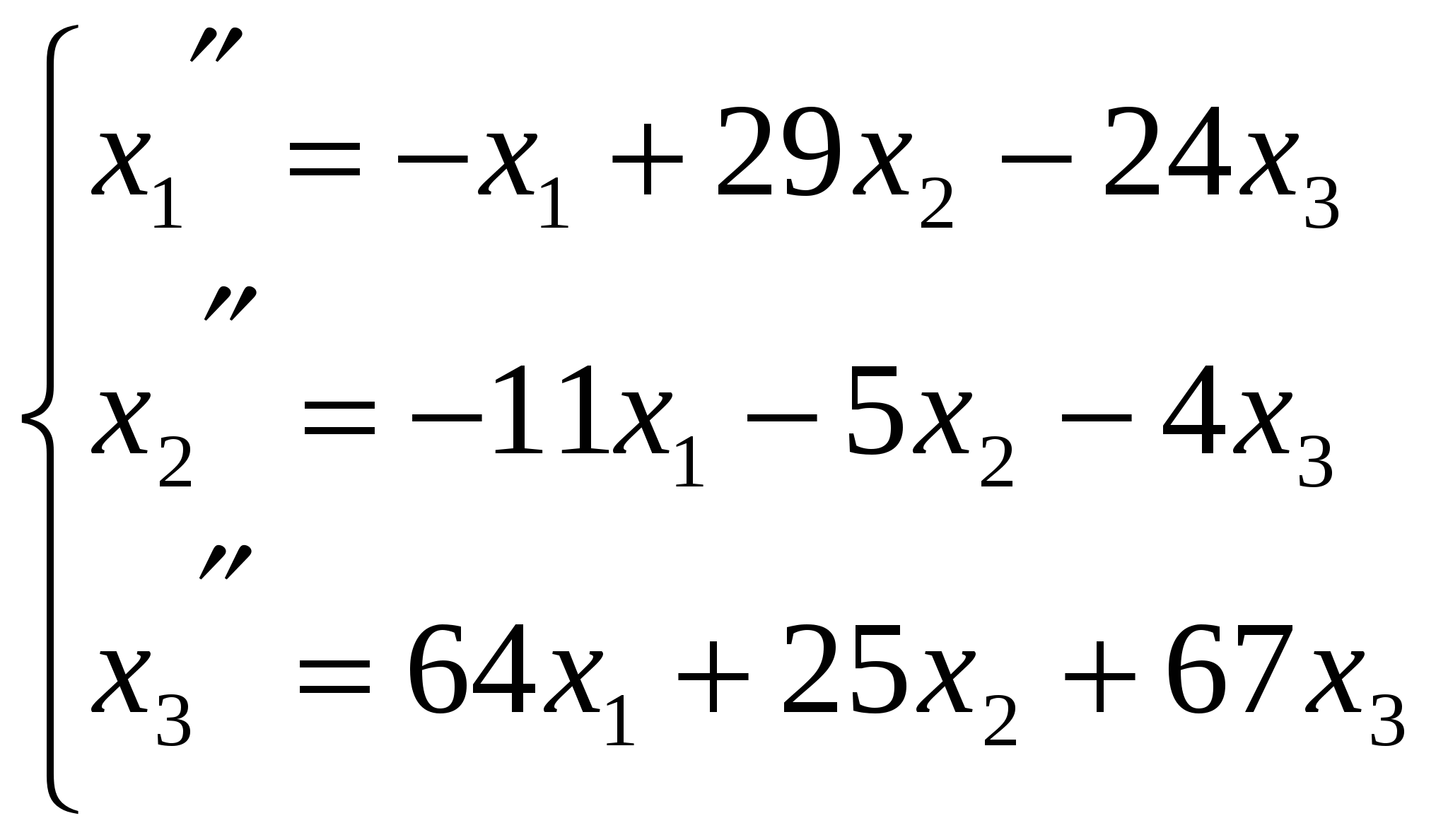 Задача 84. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей. 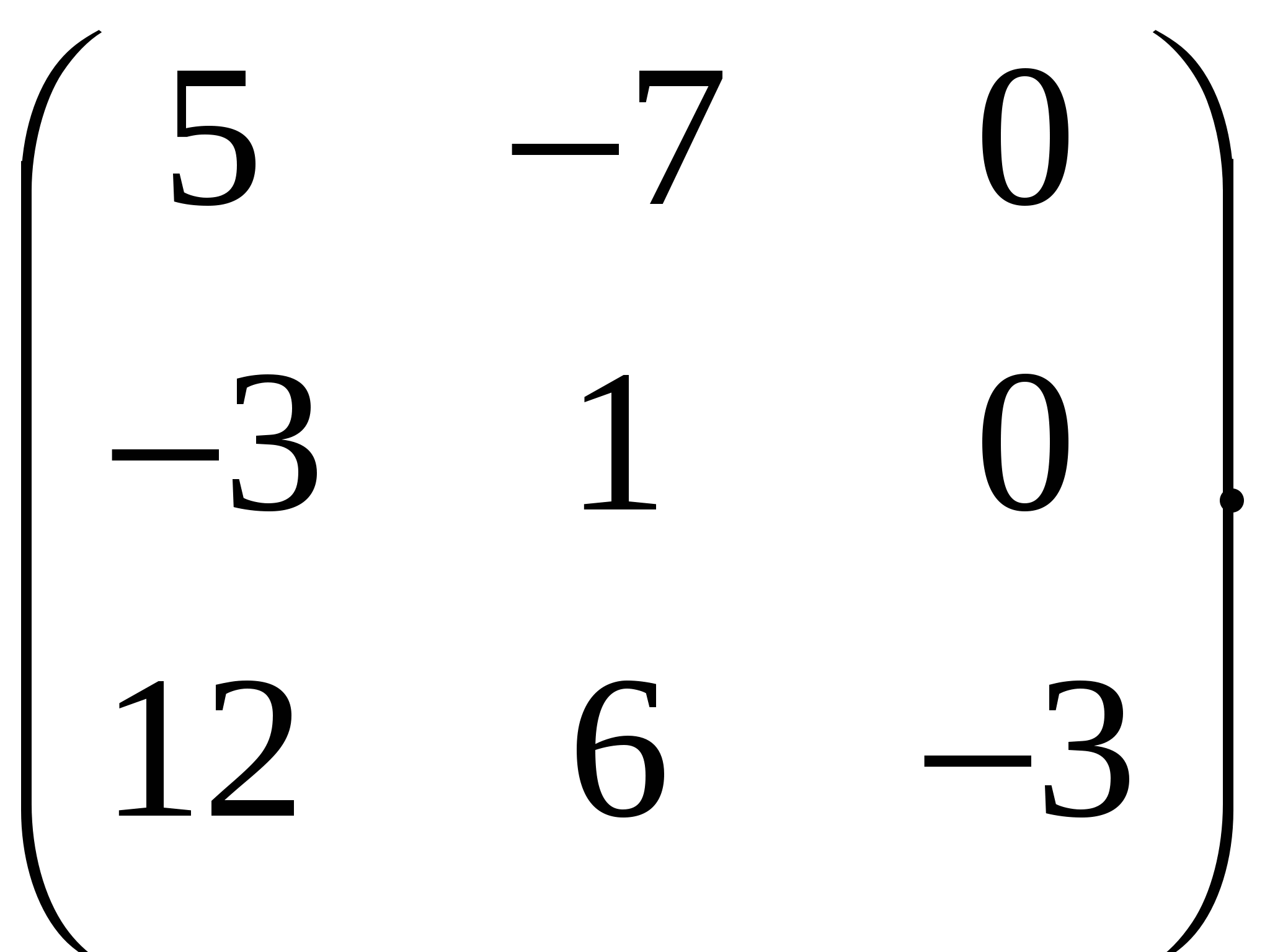 Решение:
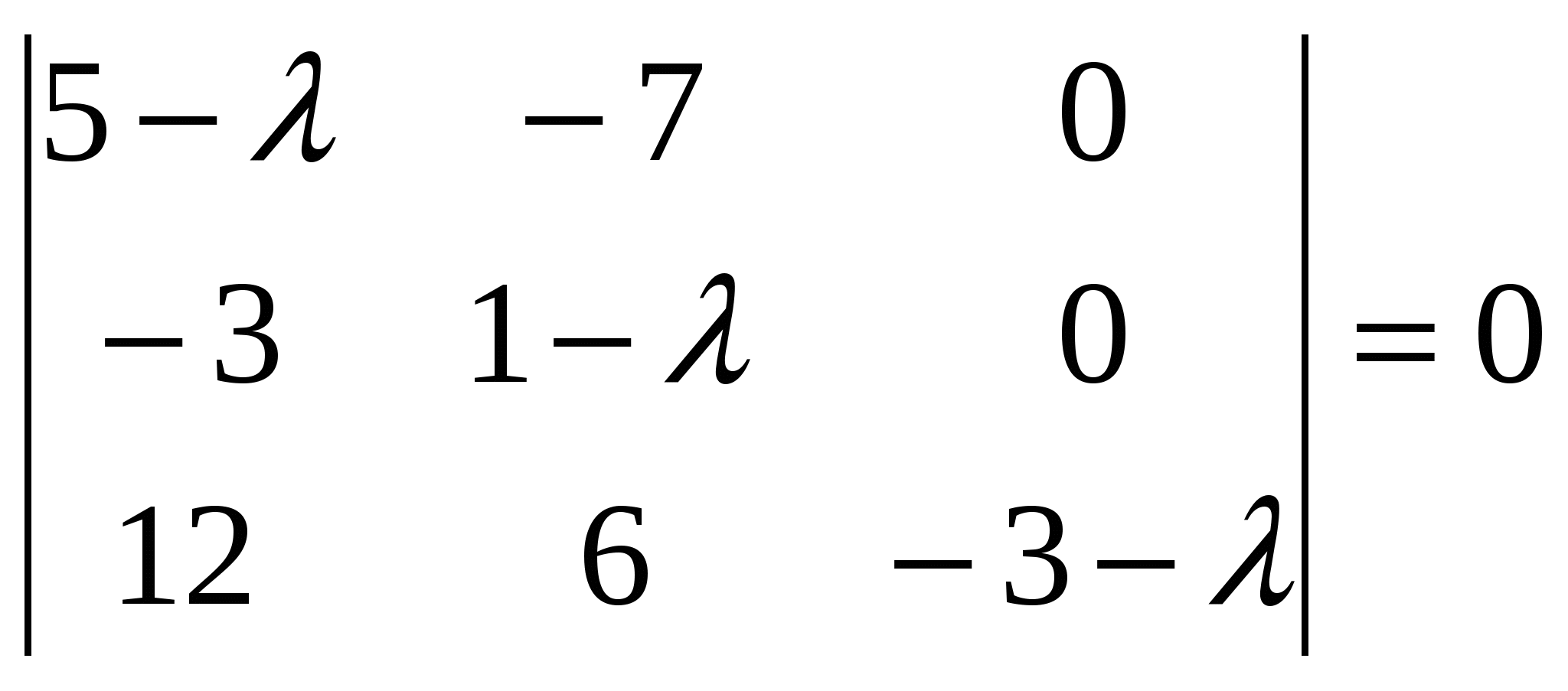 Корни этого уравнения следующие:
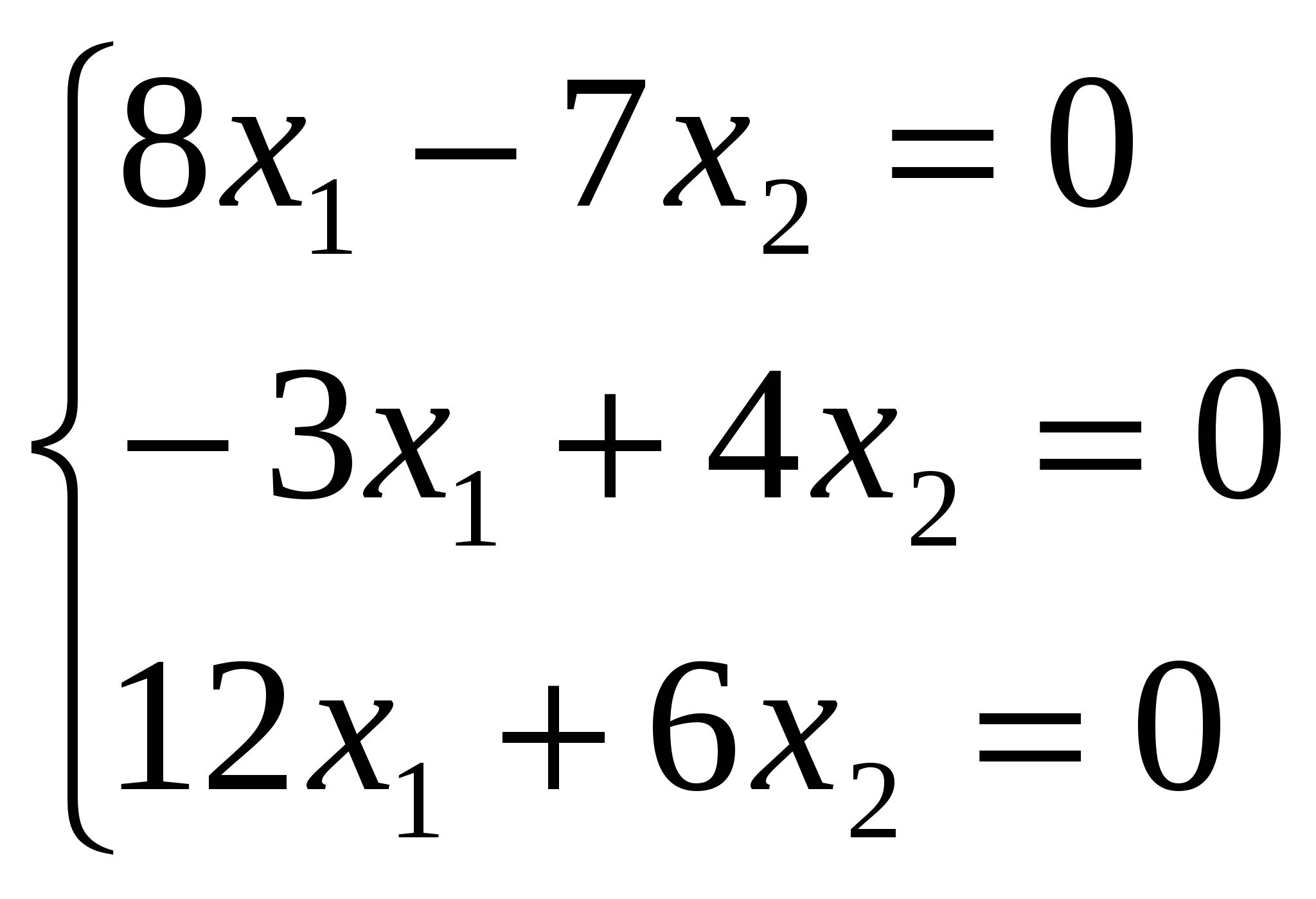 Решение этой системы можно записать в виде Вектор
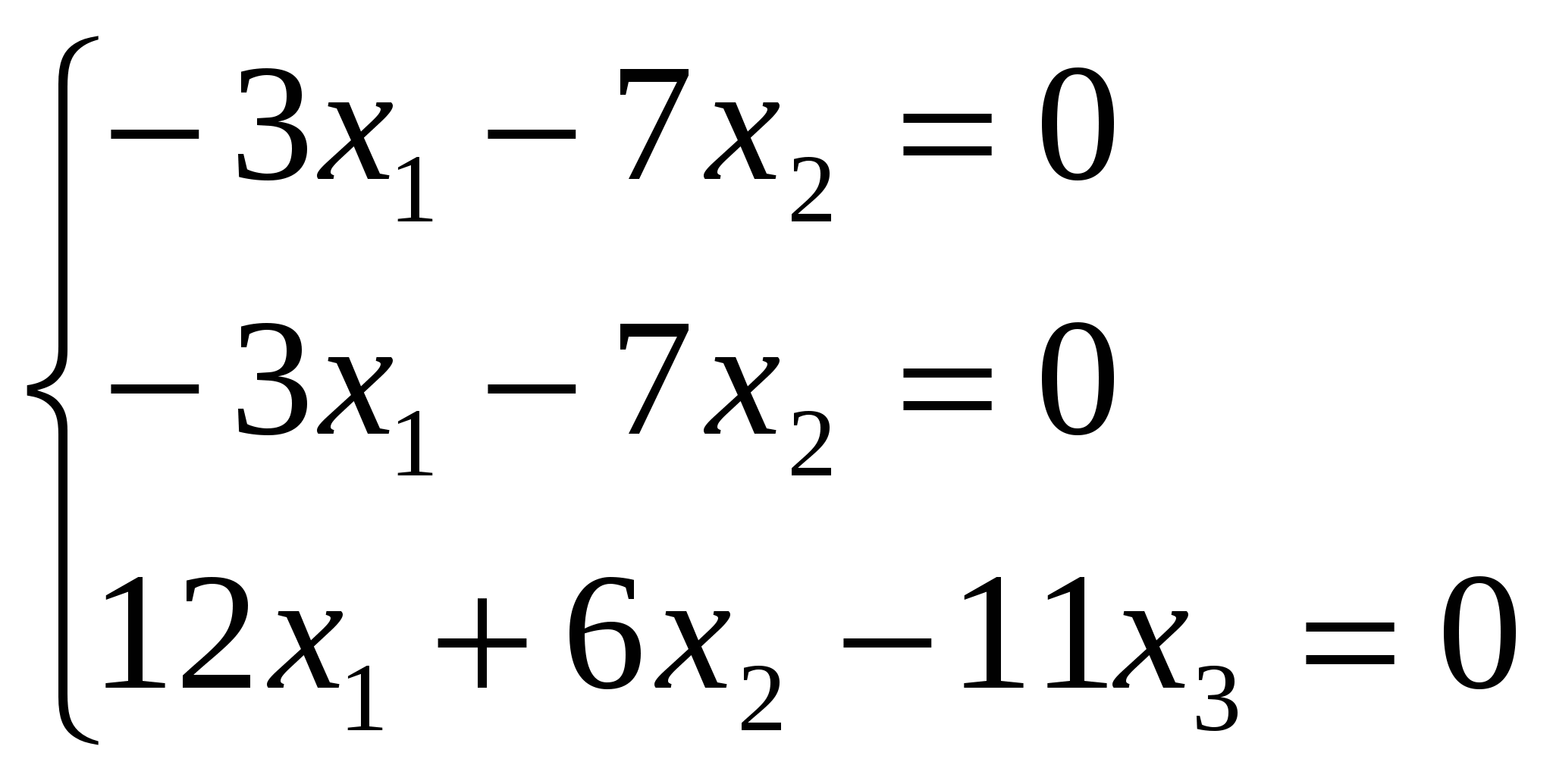 Вектор
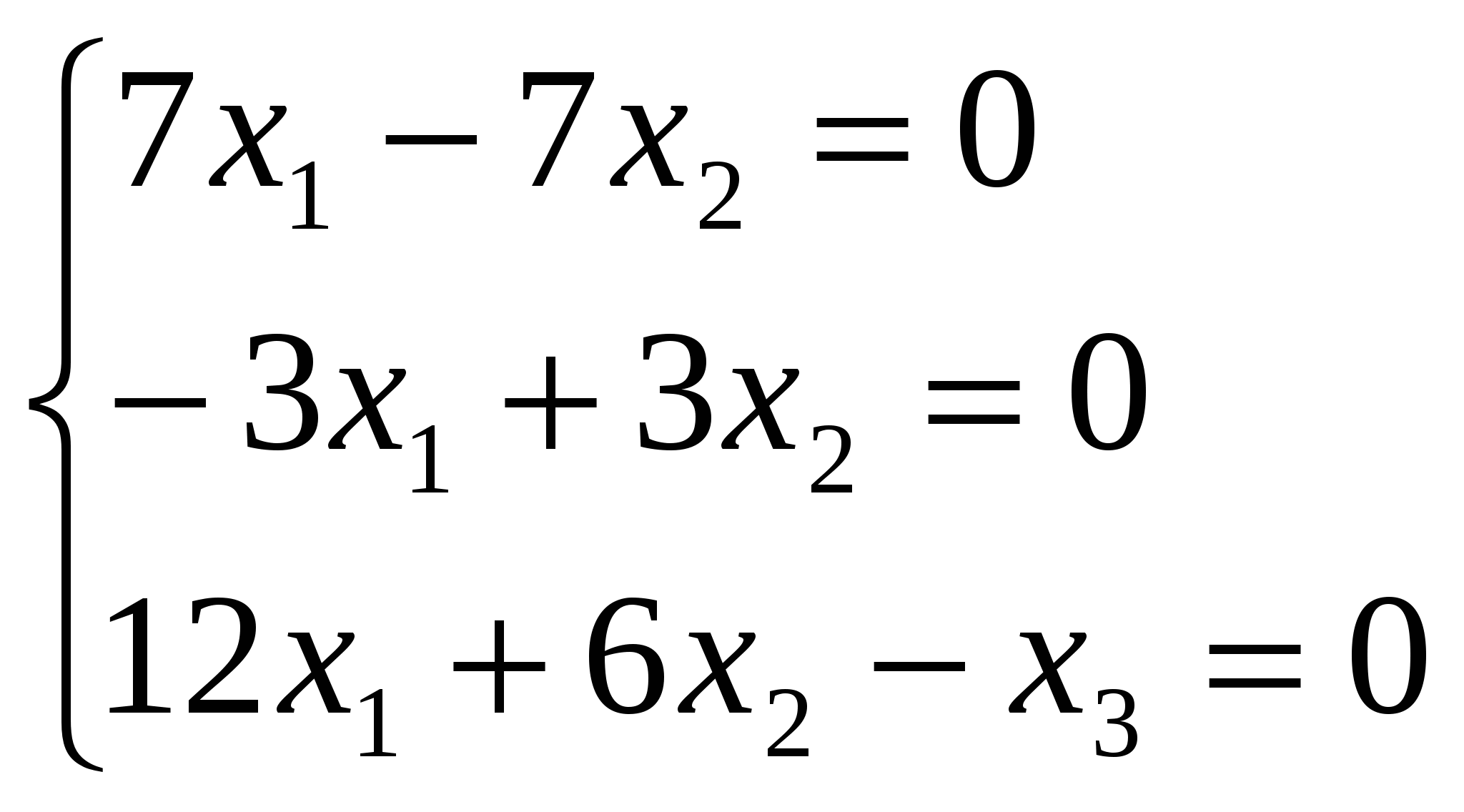 Вектор Задача 94. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм. Решение: Введем обозначение Найдем собственные значения этой матрицы. Ее характеристическое уравнение имеет вид откуда 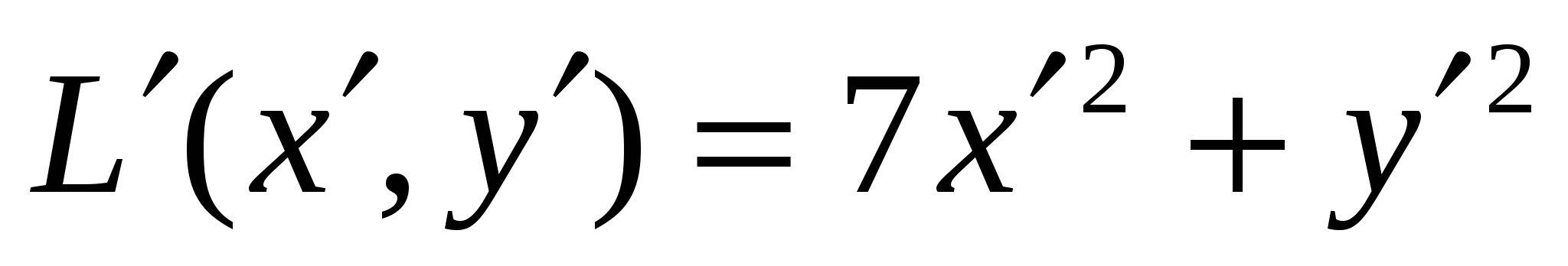 . Переходя к исходному уравнению, получаем . Переходя к исходному уравнению, получаем 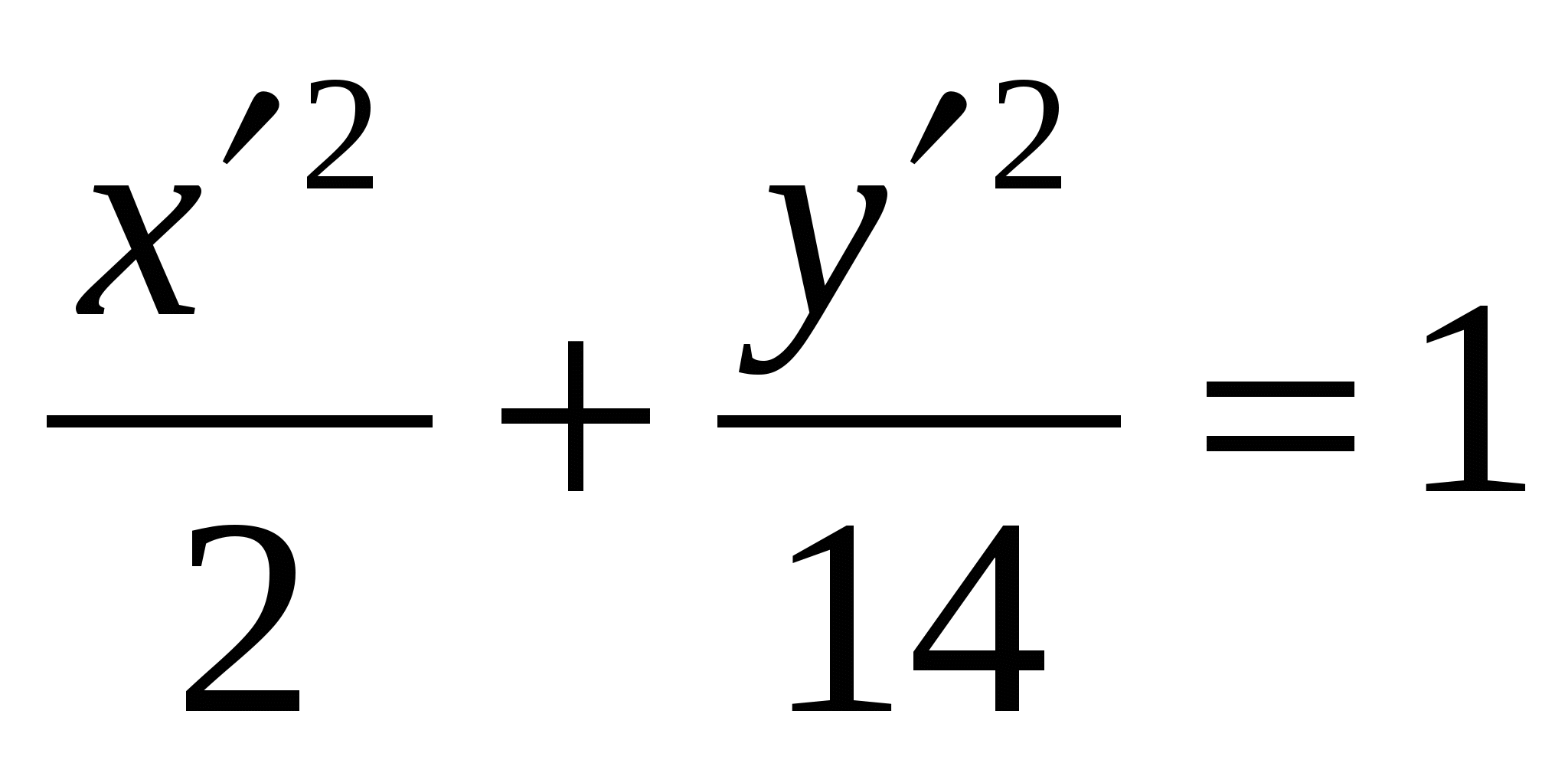 Задача 104. Построить график функции 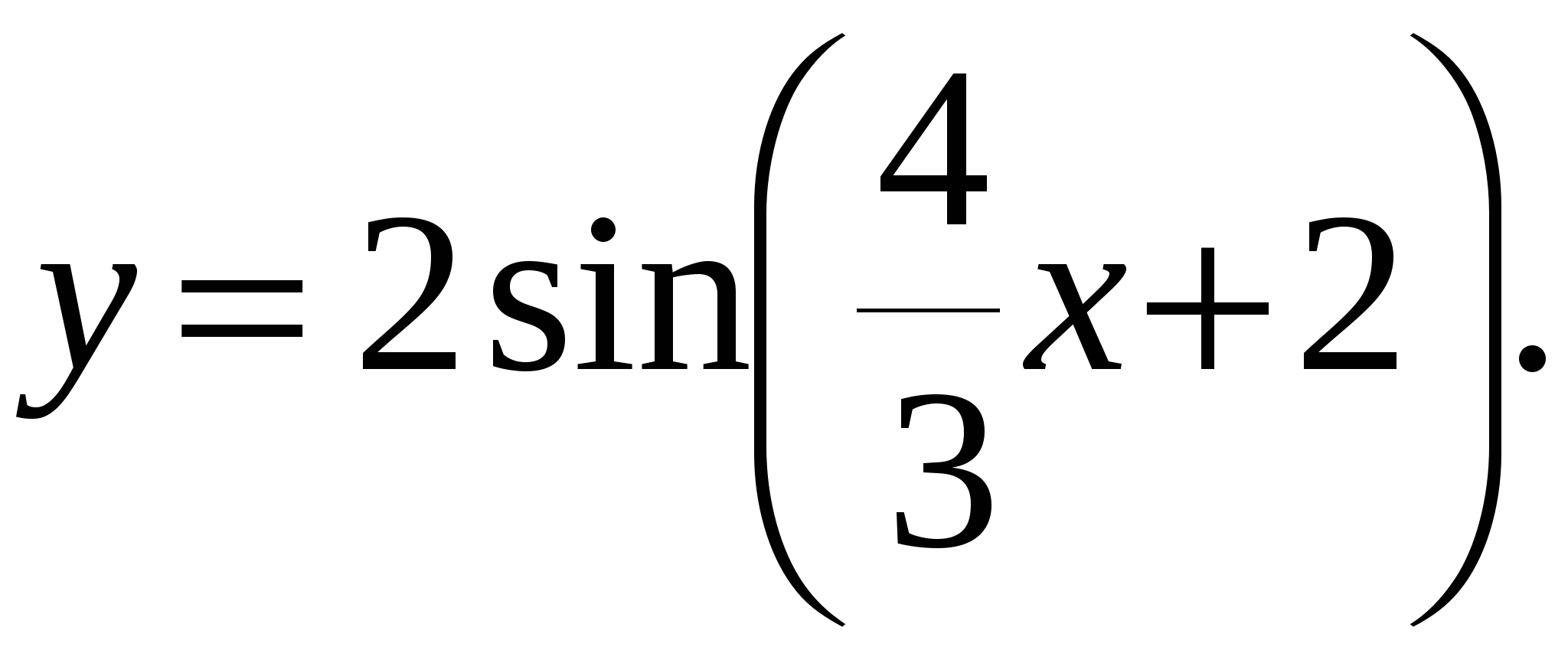 Решение:

растяжением в растяжением в и последующим параллельным переносом по оси  |
