Все задачи. Решение Как известно, базисом в пространстве является любая упорядоченная система из трёх линейно независимых векторов. Покажем, что векторы, и линейно независимы, т е. выполняется равенство
 Скачать 1 Mb.
|
|
Задача 114. Дана функция  на отрезке  . Требуется: 1) построить график функции в полярной системе координат по точкам, давая значения через промежуток /8, начиная от =0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.  Решение: 1) построим график функции в полярной системе координат по точкам, давая значения через промежуток /8, начиная от =0;
 2) найдем уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью. Из условия   , с другой стороны,  , отсюда  ; но  , следовательно, Искомое уравнение – это уравнение параболы  с вершиной в т.  . График пересекает ось Х в т.  и  Координаты т. С  , т.  , т.   Задача 124. Найти указанные пределы, не пользуясь правилом Лопиталя. а)  б)  в)  г)  Решени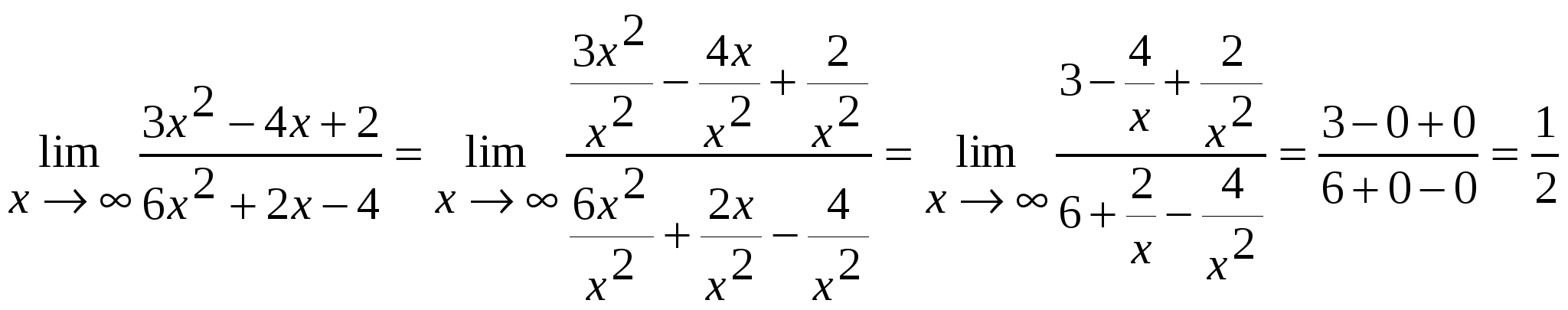е: а)  б) 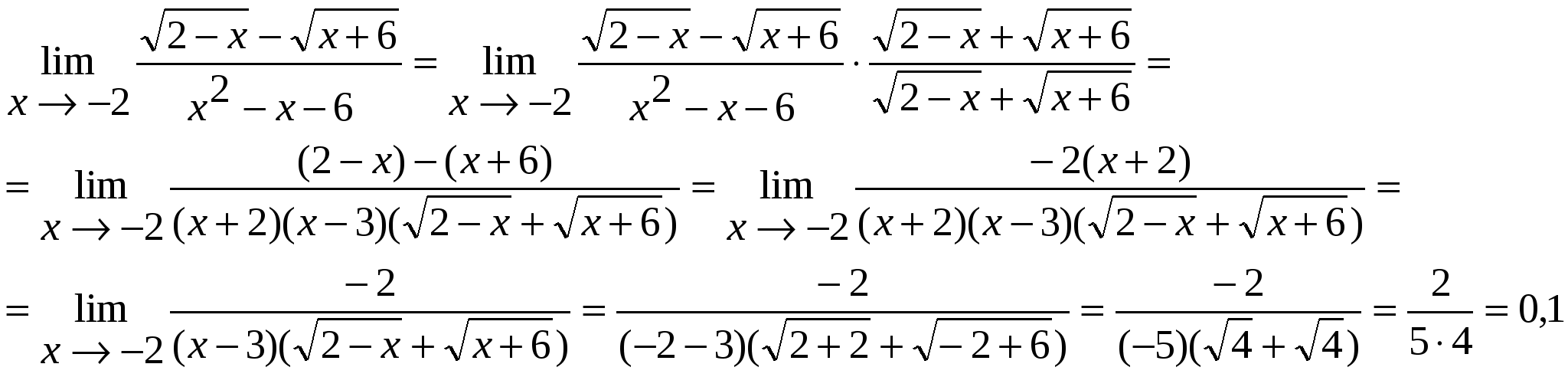 в) 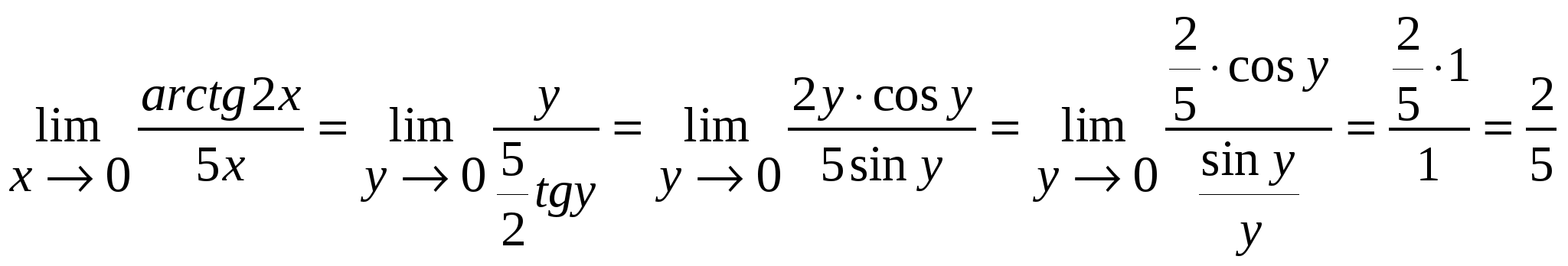 Полагая  , имеем . Тогда г) 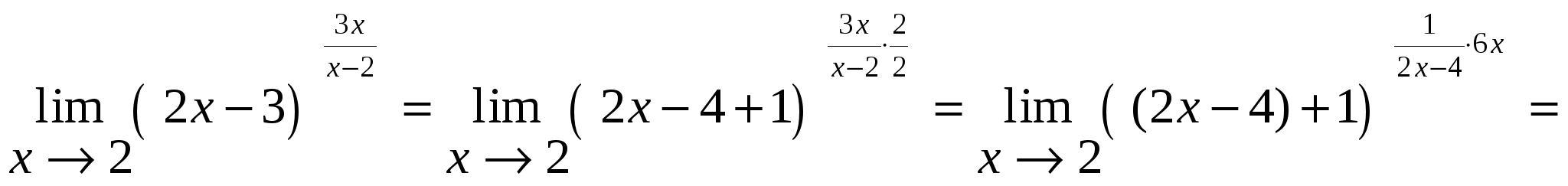 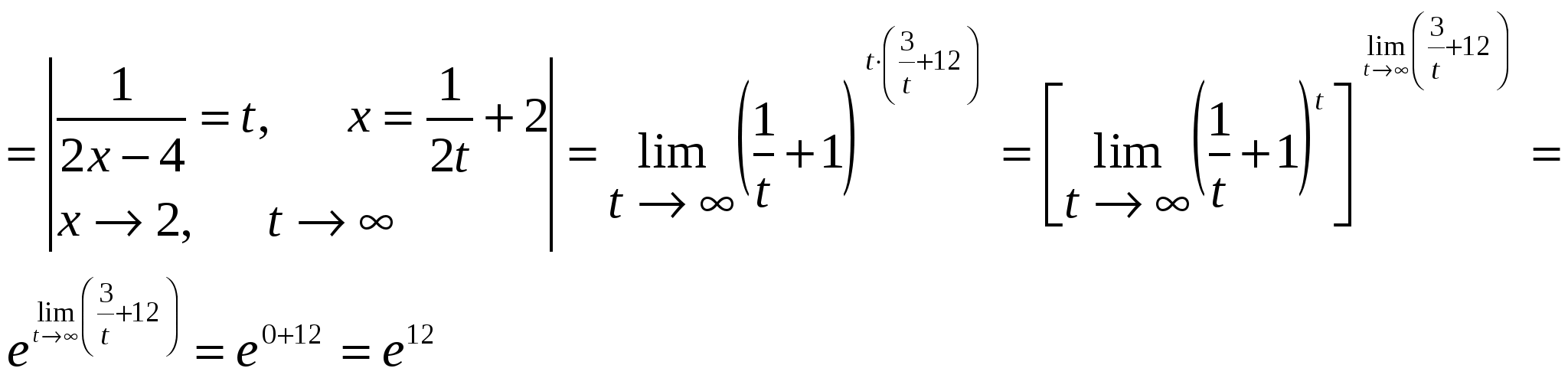 Задача 134. Заданы функция  и два значения аргумента  и  . Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж.    Решение: Функция  и неопределенна в т Следовательно в т.  разрыва нет, а т.  - точка разрыва. Т.к.   и т. не принадлежит области определения функции, то при функция имеет точку разрыва второго рода (бесконечный скачок). Для схематического построения графика функции  найдем  .   Задача 144. Задана функция 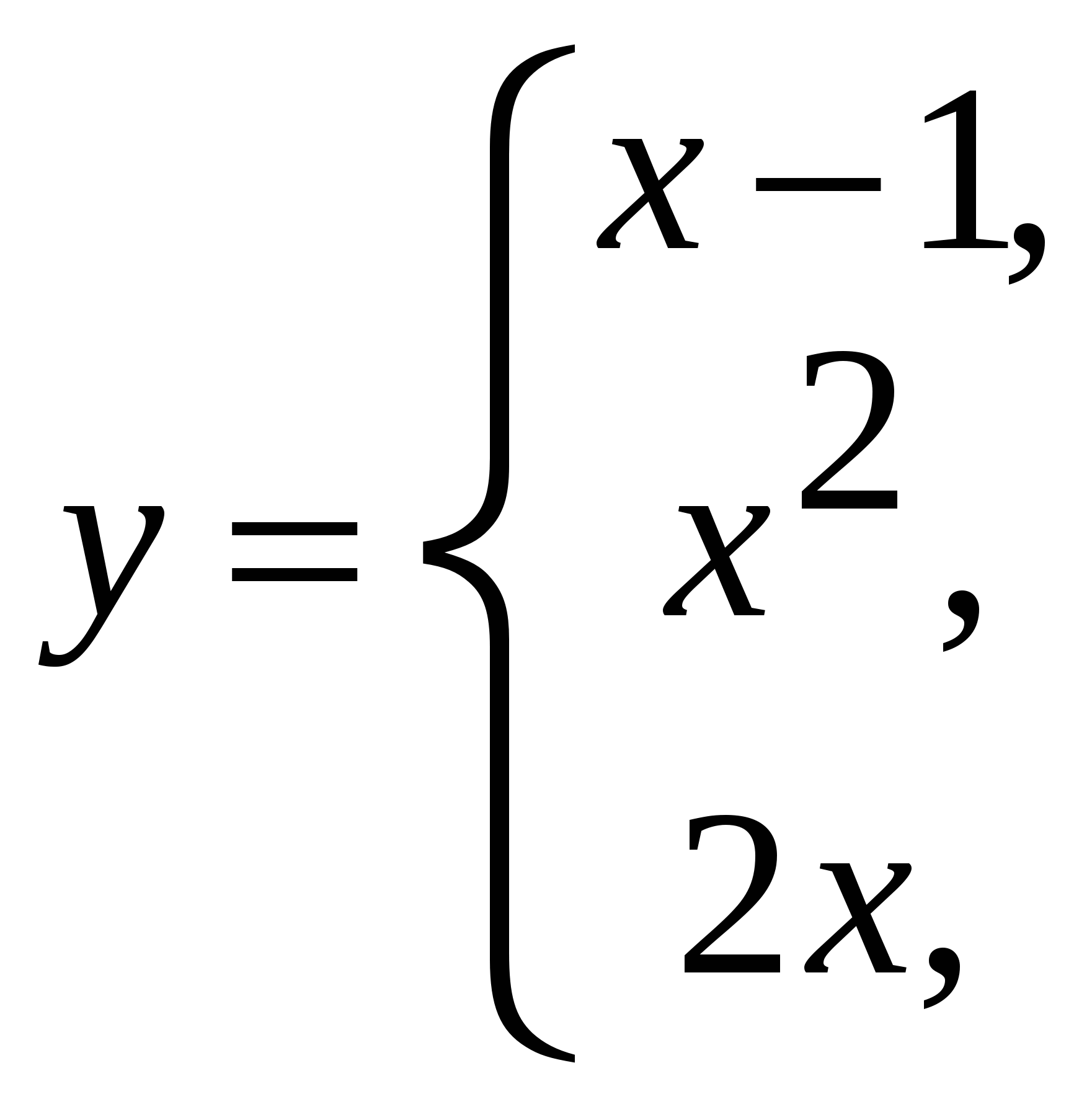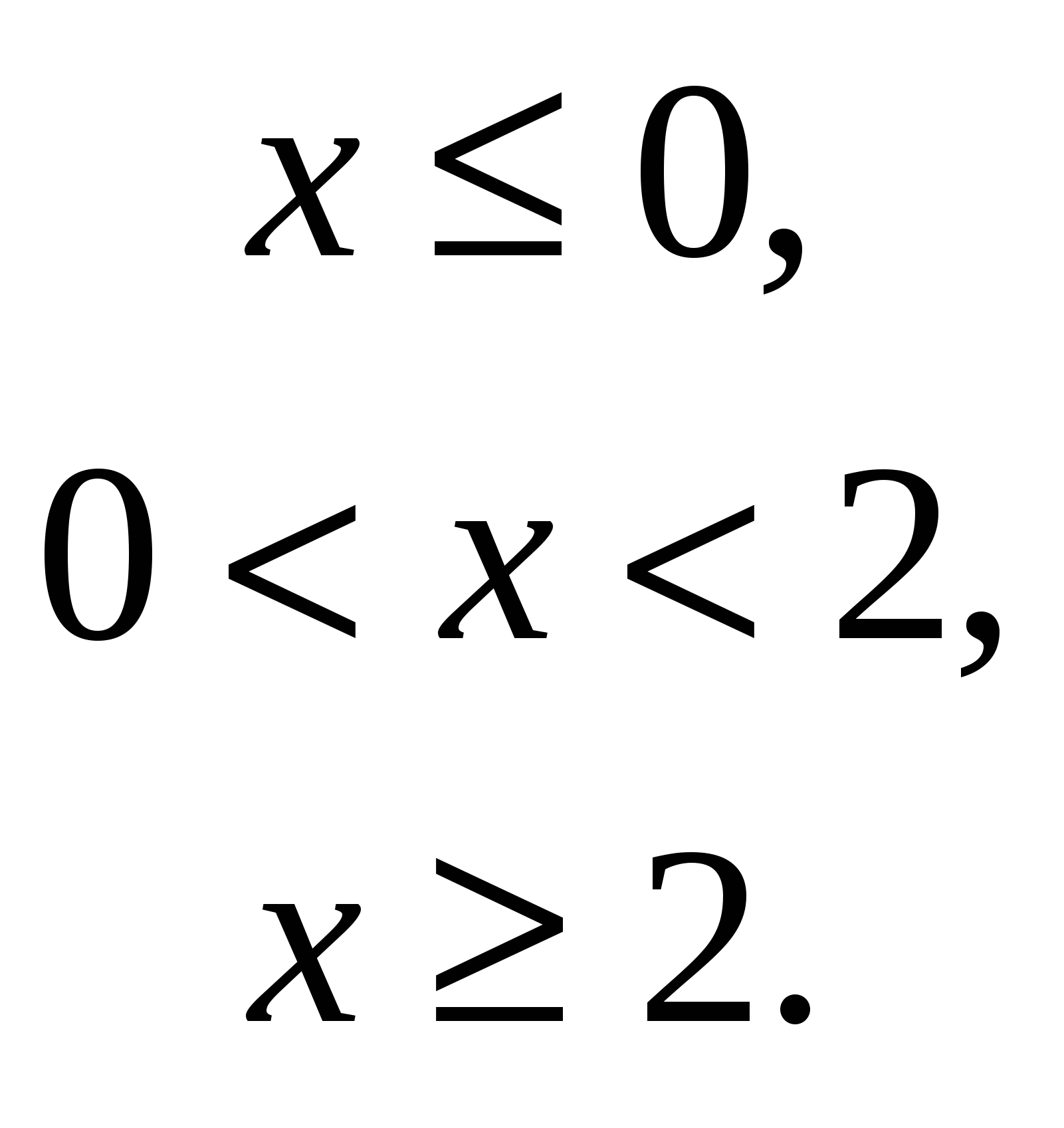различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.  Решение: Область определения функции  - вся числовая ось  . Разрывы возможны только в точках  и  , в которых изменяется аналитическое задание функции. Найдем односторонние пределы в т. и значение функции в этой точке:  Т.к. в т. функции определена, конечные односторонние пределы существуют и не равны между собой, то т. - точка разрыва первого рода.Найдем односторонние пределы в т.  и значение функции в этой точке:  Т.к. в т. функции определена, конечные односторонние пределы существуют и равны между собой, то в т. функция непрерывна. |
