Математика. Задачи 8, 9.. Решение 1 2 3 4
 Скачать 22.61 Kb. Скачать 22.61 Kb.
|
|
Задача 8. Векторы и операции над ними. Точки А, В, С пространства заданы своими координатами в прямоугольной декартовой системе координат. Найти: векторы 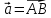 , ,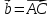 , ,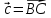 ; ;скалярное произведение 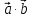 ; ;векторное произведение 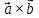 и его модуль; и его модуль;величины углов, длины сторон и площадь треугольника АВС; смешанное произведение 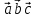 ; ;уравнение плоскости, проходящей через точки A, B, C. 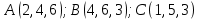 Решение: 1) 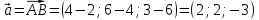 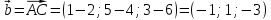 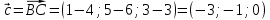 2) 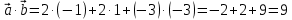 3) 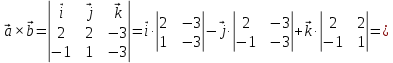 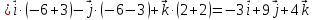 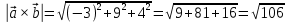 4) Угол А образован векторами 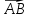 и и 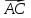 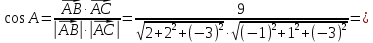 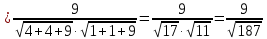 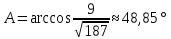 Угол B образован векторами 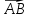 и и  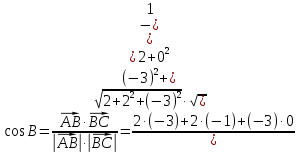 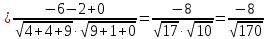 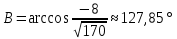 Но в нашем случае это смежный угол, угол B равен 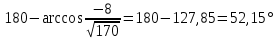 Угол C образован векторами 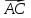 и и 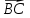 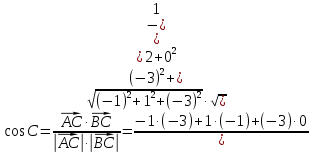 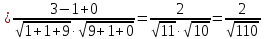 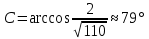 Выполним проверку. Сумма углов треугольника должна равняться 180° 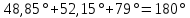 Найдем стороны треугольника 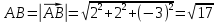 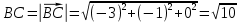 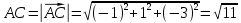 Площадь треугольника ABC найдем через векторное произведение векторов 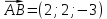 и и 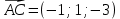 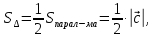 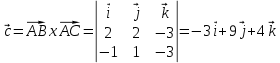 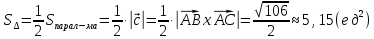 5) 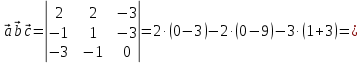 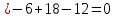 6) 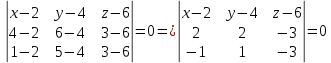 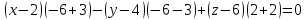 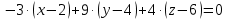 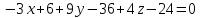 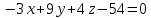 Задача 9. Системы линейных алгебраических уравнений и методы их решения. Дана система линейных неоднородных уравнений. Доказать её совместность и решить систему уравнений тремя способами: методом Гаусса; по формулам Крамера и с помощью обратной матрицы. 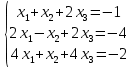 Решение: Матрицы А и B 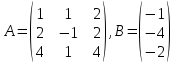 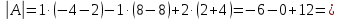 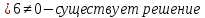 Метод Гаусса Запишем расширенную матрицу системы 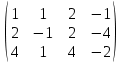 Вычтем из второй строки первую, умноженную на 2, из третьей первую, умноженную на 4 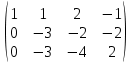 Вычтем из третьей строки вторую 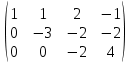 Поделим вторую строку на -3, а третью на -2 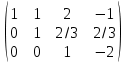 Запишем получившуюся систему 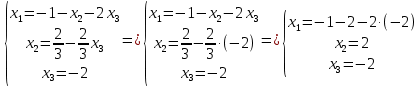 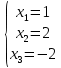 Выполним проверку 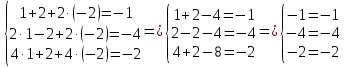 Метод Крамера Составим матрицу коэффициентов и матрицу свободных членов 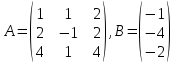 Найдем определитель матрицы А 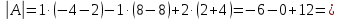 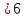 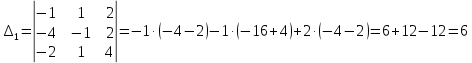 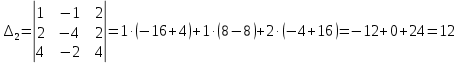 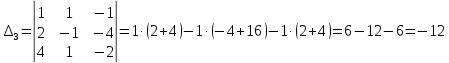 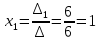 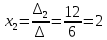 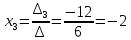 Метод обратной матрицы Пусть 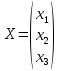 – матрица решений системы уравнений – матрица решений системы уравненийТогда 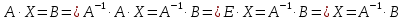 Найдем обратную матрицу 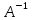 Найдем алгебраические дополнения определителя матрицы А 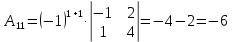 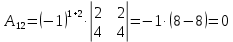 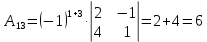 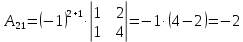 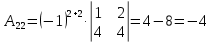 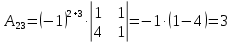 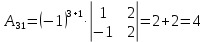 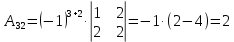 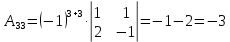 Тогда обратная матрица имеет вид 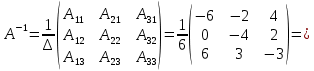 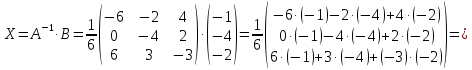 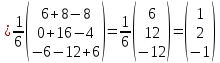 |
