| 1 КАТЕГОРИЯ
| |
| Какому числу может равняться ранг матрицы 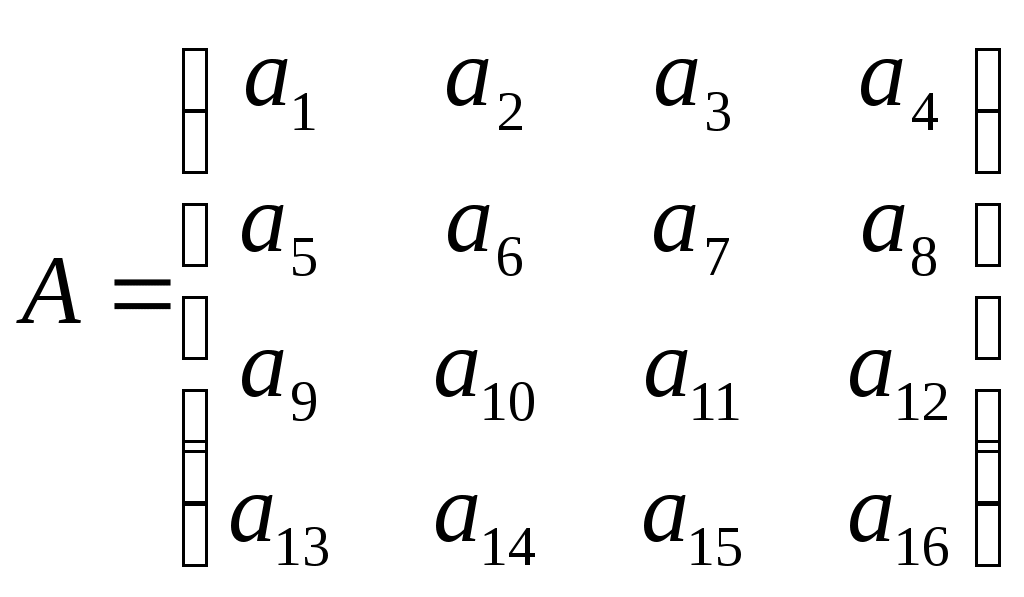 ? ? | 1. 10
2. 1
3. -2
4. 5
|
| Ранг матрицы 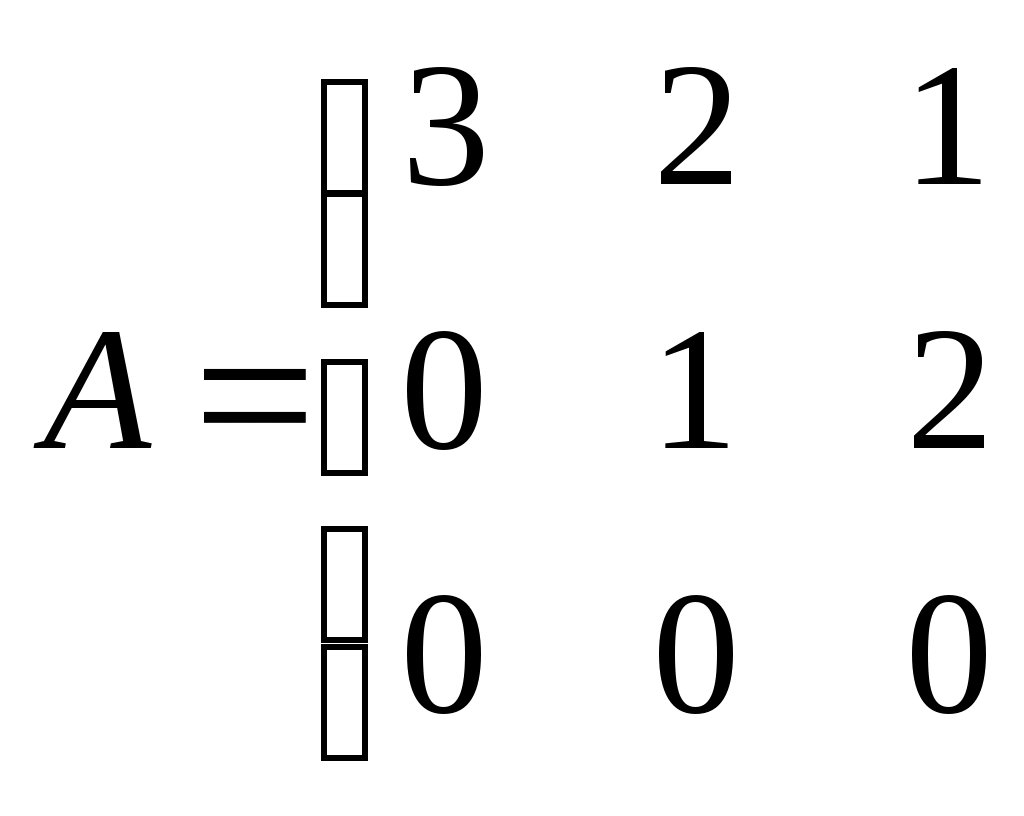 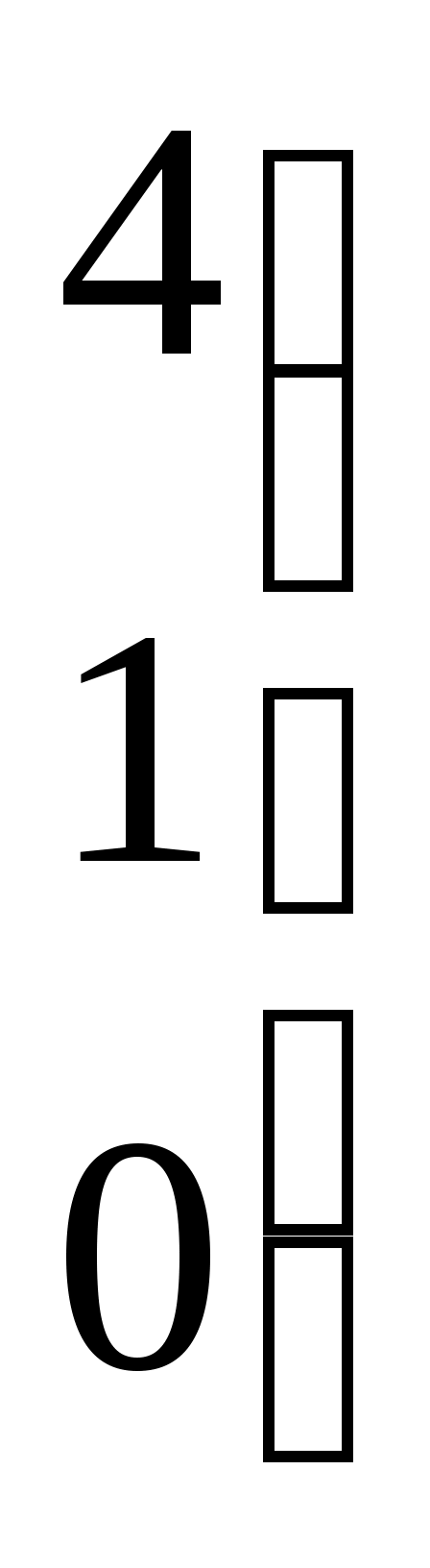
равен
| 1. 2
2. 1
3. 0
4. 3
|
|
Определитель нулевой квадратной матрицы равен
|
1.0 2.1 3.3 4.зависит от размерности матрицы
|
| Какая матрица является вырожденной? |
единичная
нулевая
квадратная матрица, определитель которой равен 1
любая матрица, имеющая обратную
|
| Какие три числа образуют главную диагональ определителя ? ? |
1,2,3 2. 3,5,7
3. 1,5,9 4. 3,6,9
|
| Известно, что в системе 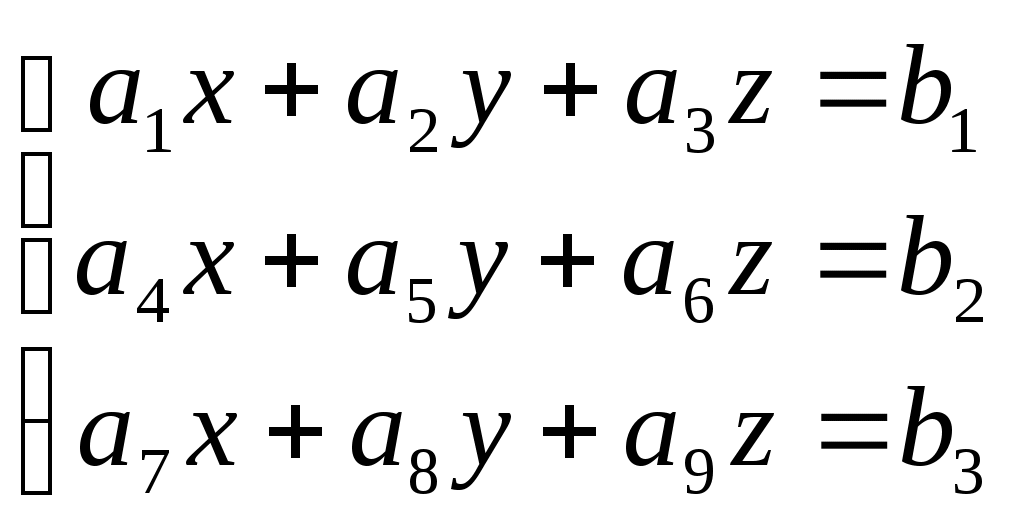
Ранг матрицы 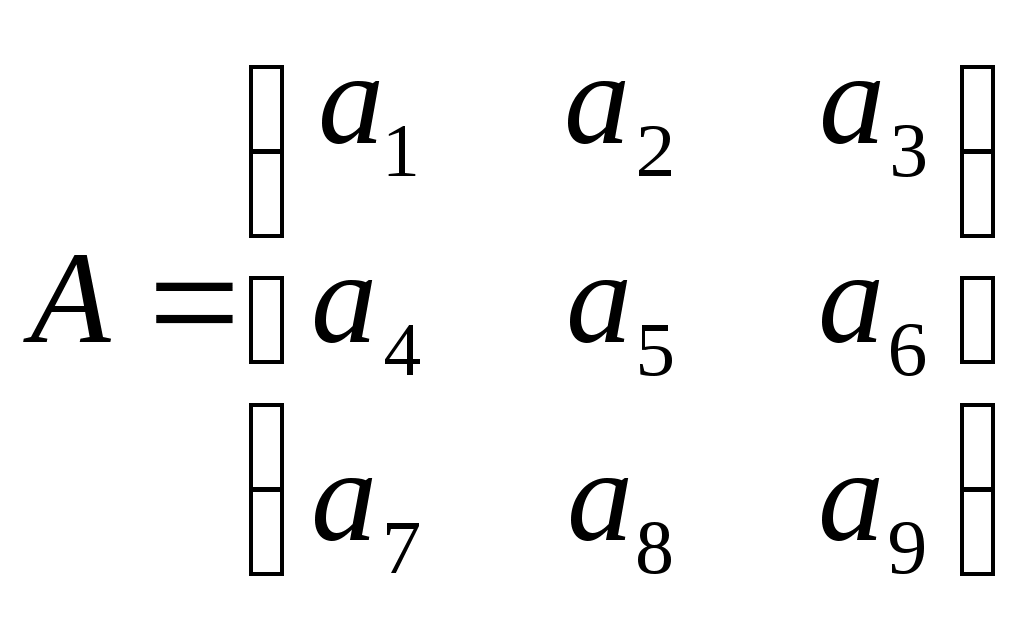 равен рангу матрицы равен рангу матрицы 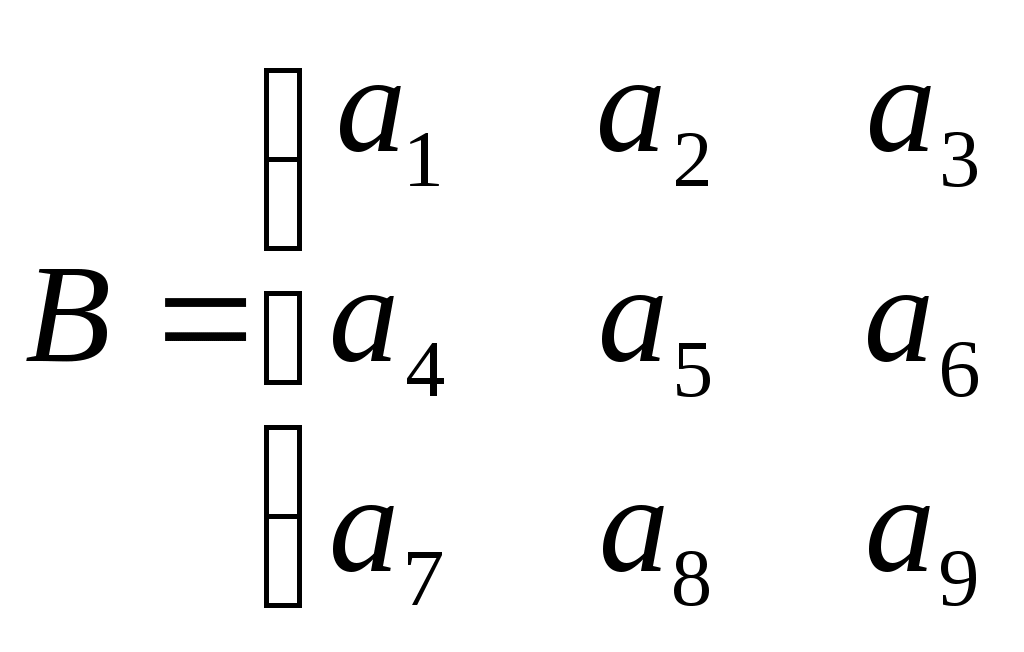 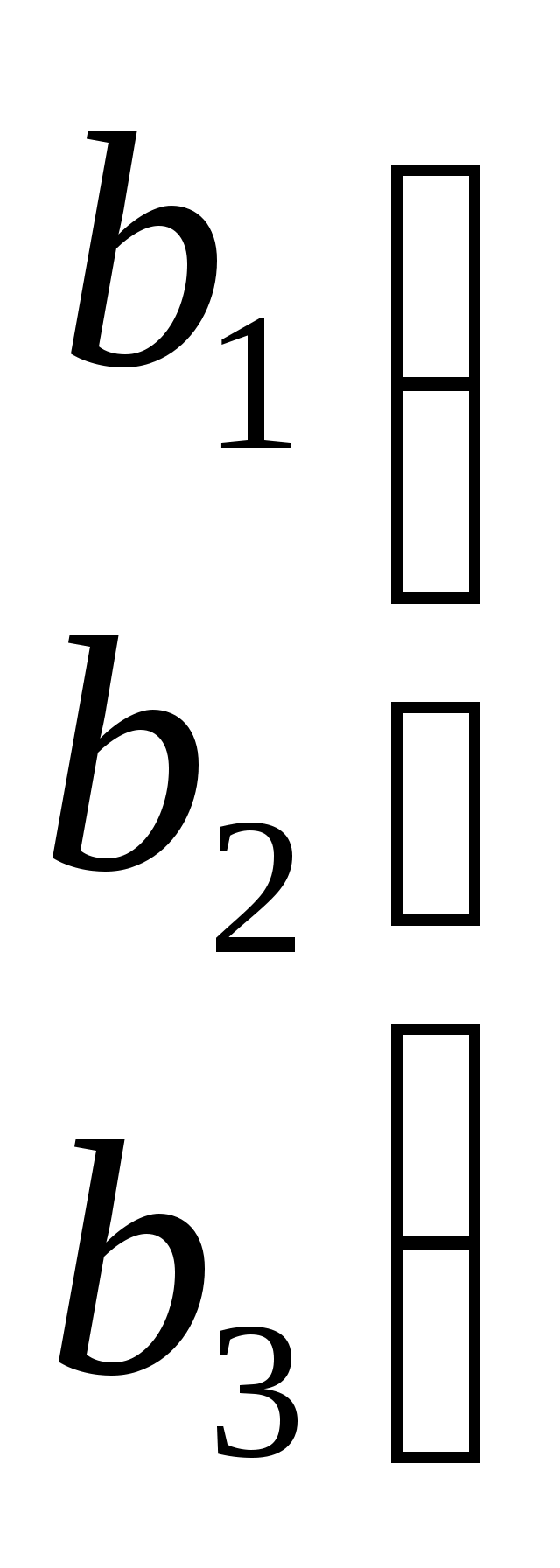 и равен 3. и равен 3.
Что можно сказать о количестве решений системы?
| 1. система имеет 2 решения
2. система не имеет решений
3. система имеет единственное решение
4. система имеет бесконечное множество решений
|
| Чему равен определитель? 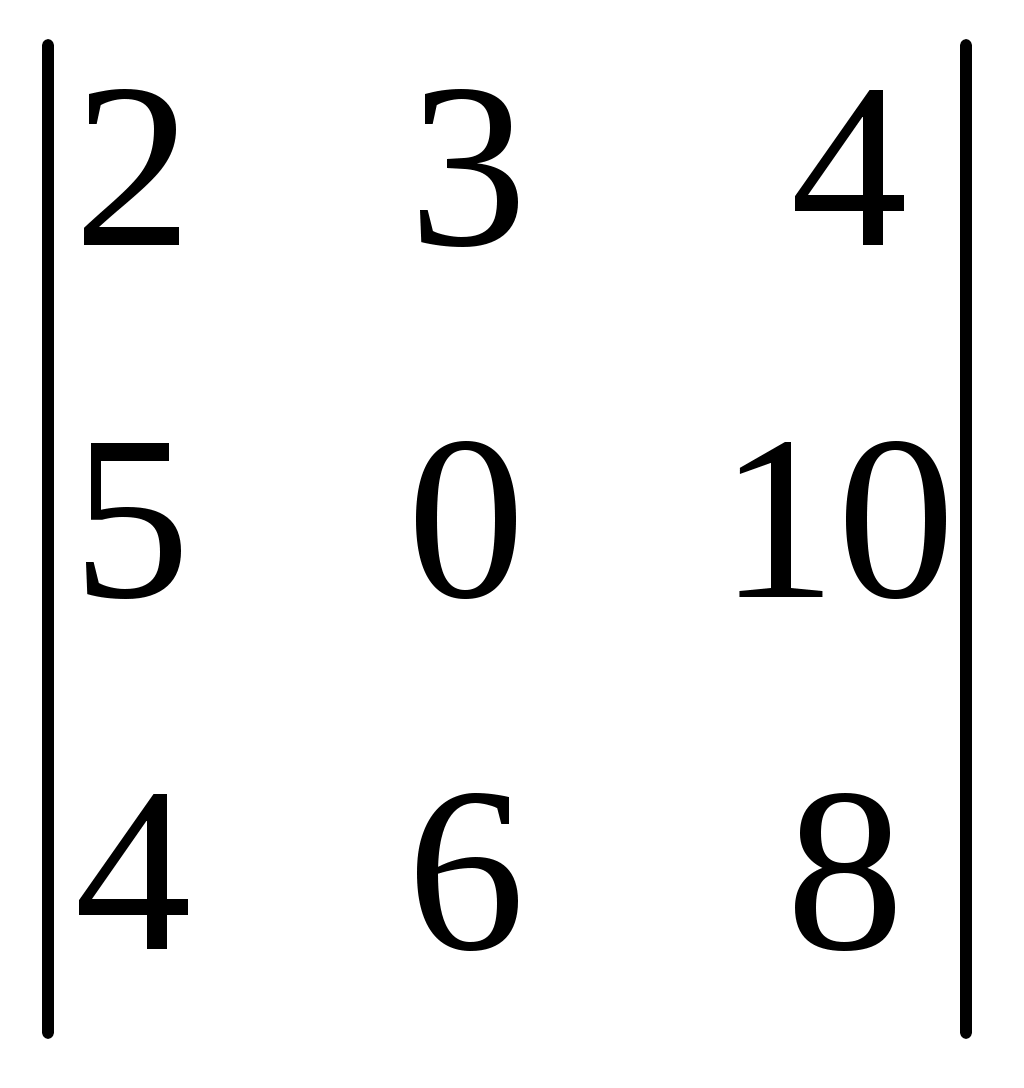 | 1. 6 2. 2 3. 0 4. 3 |
| Что можно сказать про определители  и и  ? ? |
1. их значения равны по модулю, но противоположны по знаку
2. их значения равны
3. их значения равны 0
4. их значения равны 1
|
|
Какая операция называется транспонированием матрицы?
|
1.Перемена местами двух строк или столбцов матрицы
2.Сложение всех элементов матрицы
3.Удаление строки или столбца матрицы, состоящего полностью из нулей
4.Замена всех строк матрицы соответствующими по номеру столбцами и наоборот
|
|
После преобразований расширенная матрица системы линейных алгебраических уравнений имеет вид 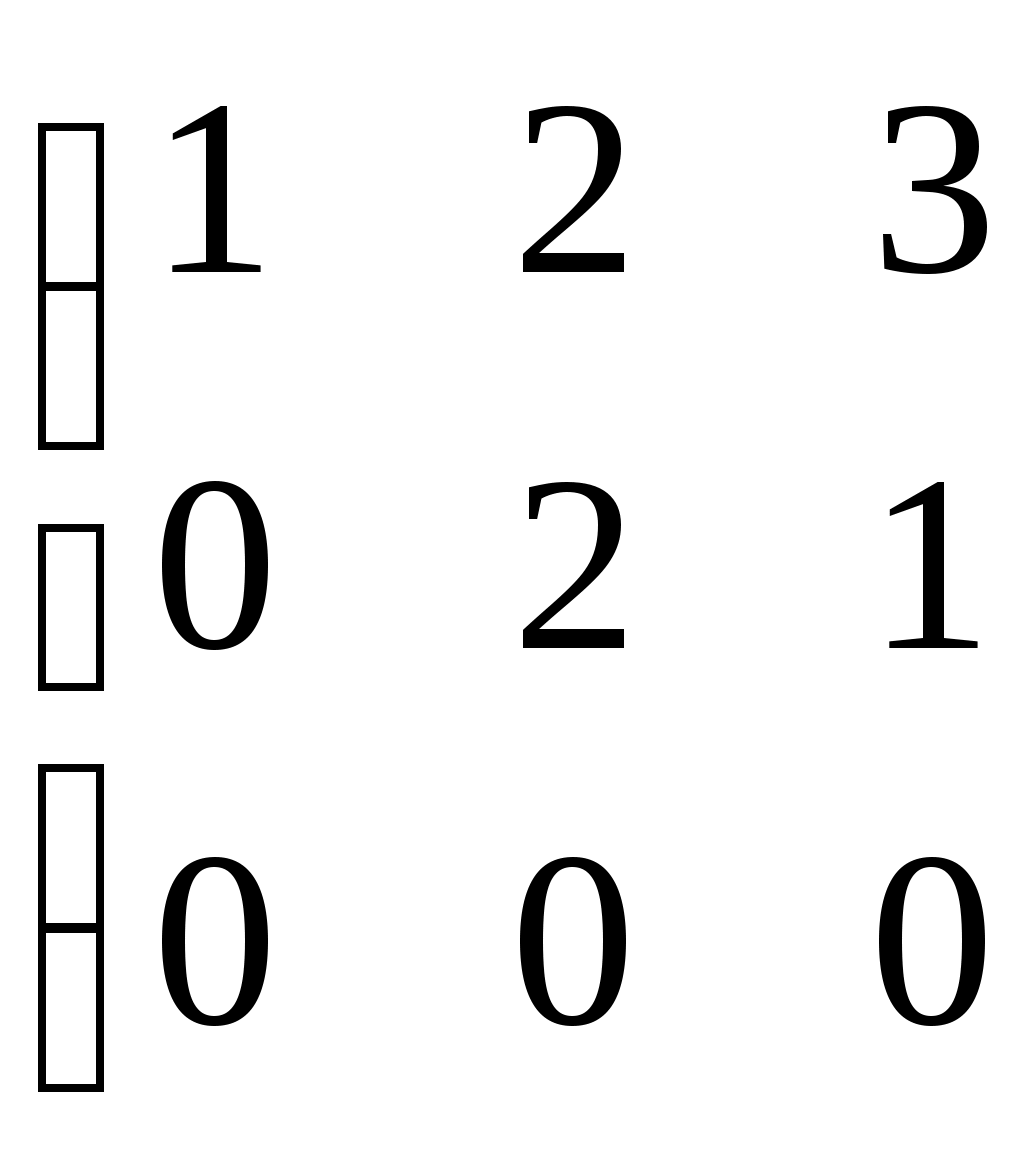 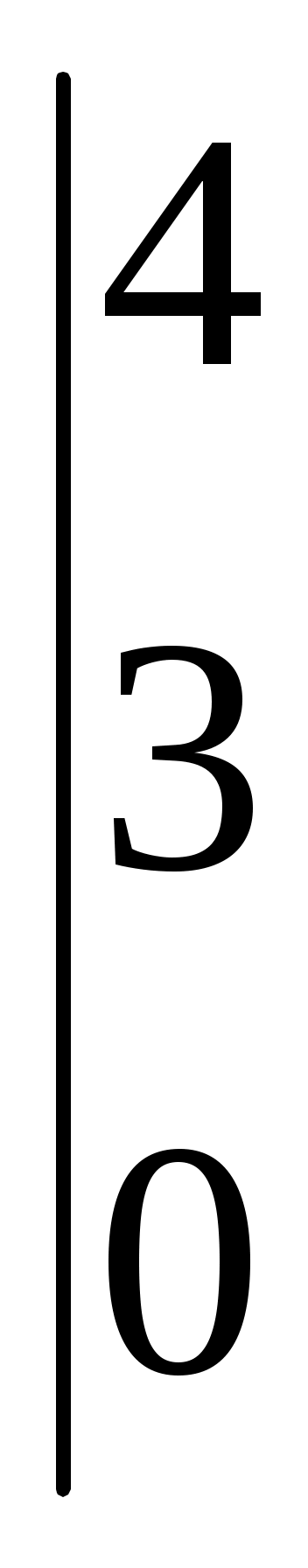  . Сколько решений имеет система? . Сколько решений имеет система?
|
бесконечное множество
два
система несовместна
одно
|
| Алгебраическое дополнение элемента 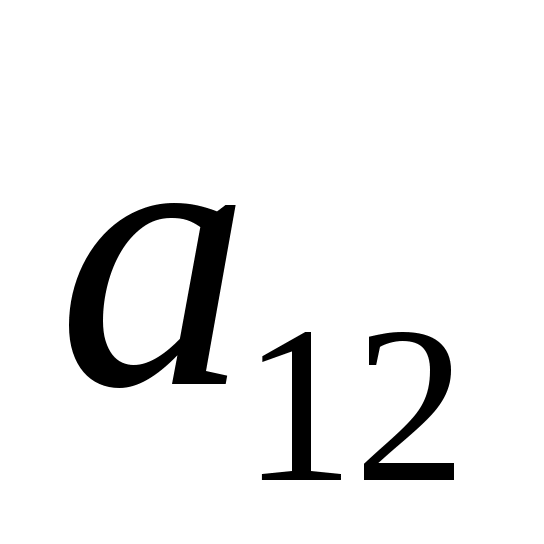 определителя определителя  равно: равно: |
1. 6
2. -6
3. 4
4. -4
|
| Какие матрицы складывать нельзя? | 1.  и и 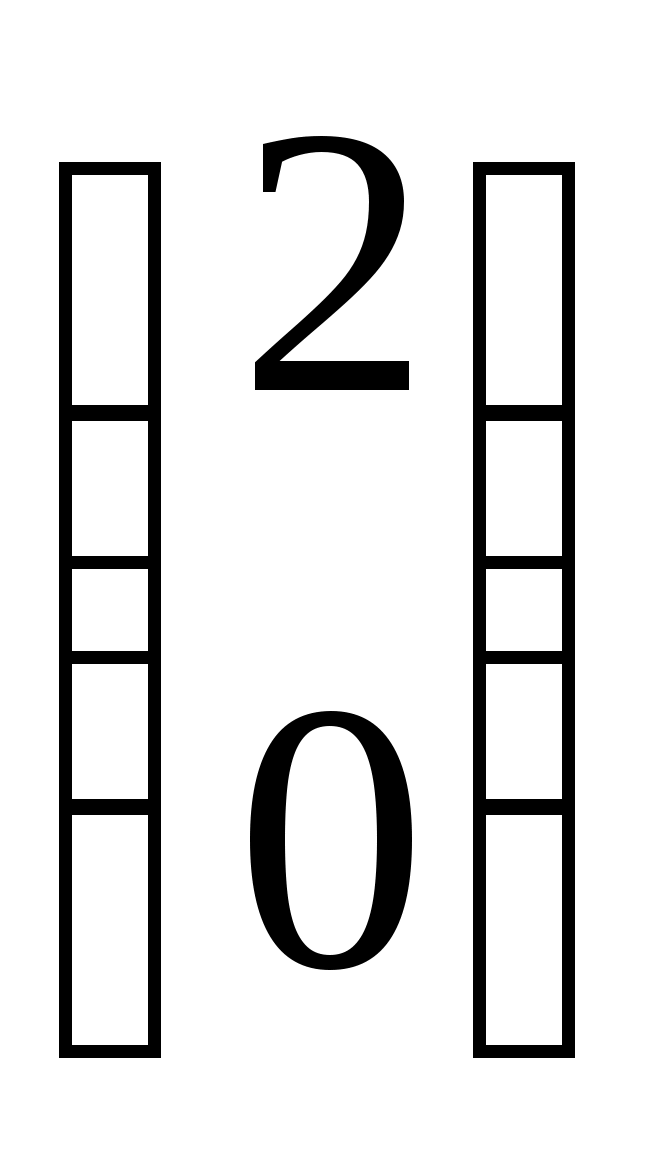 2. 2. 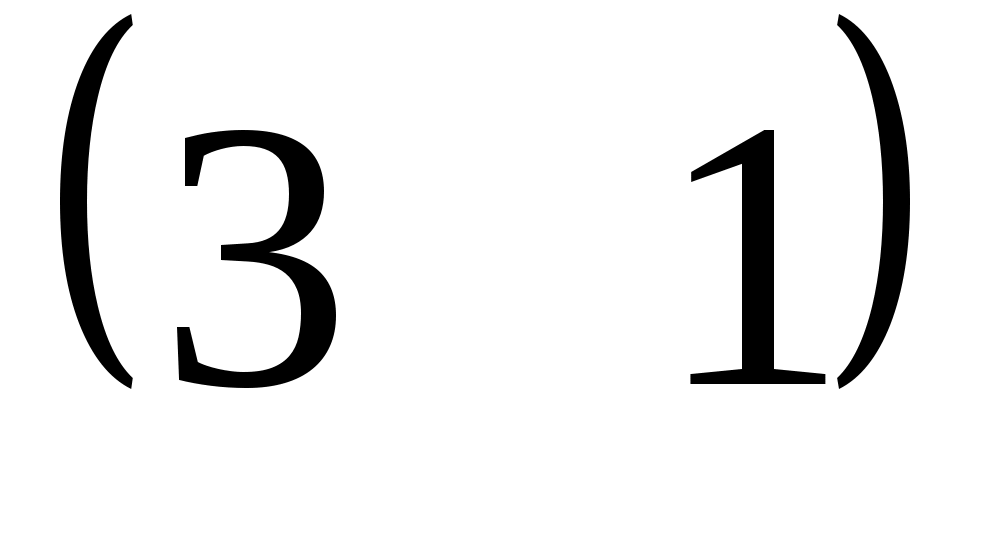 и и 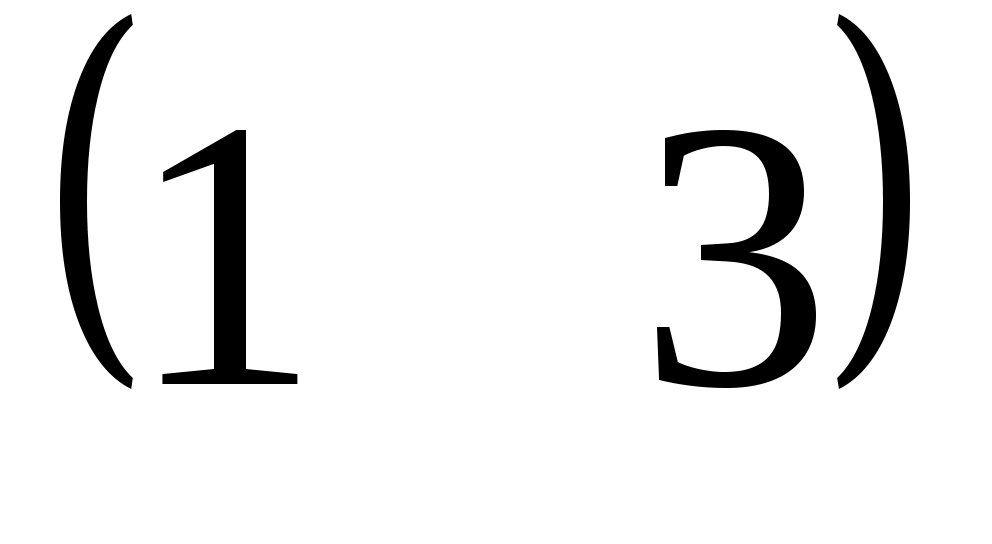
3. 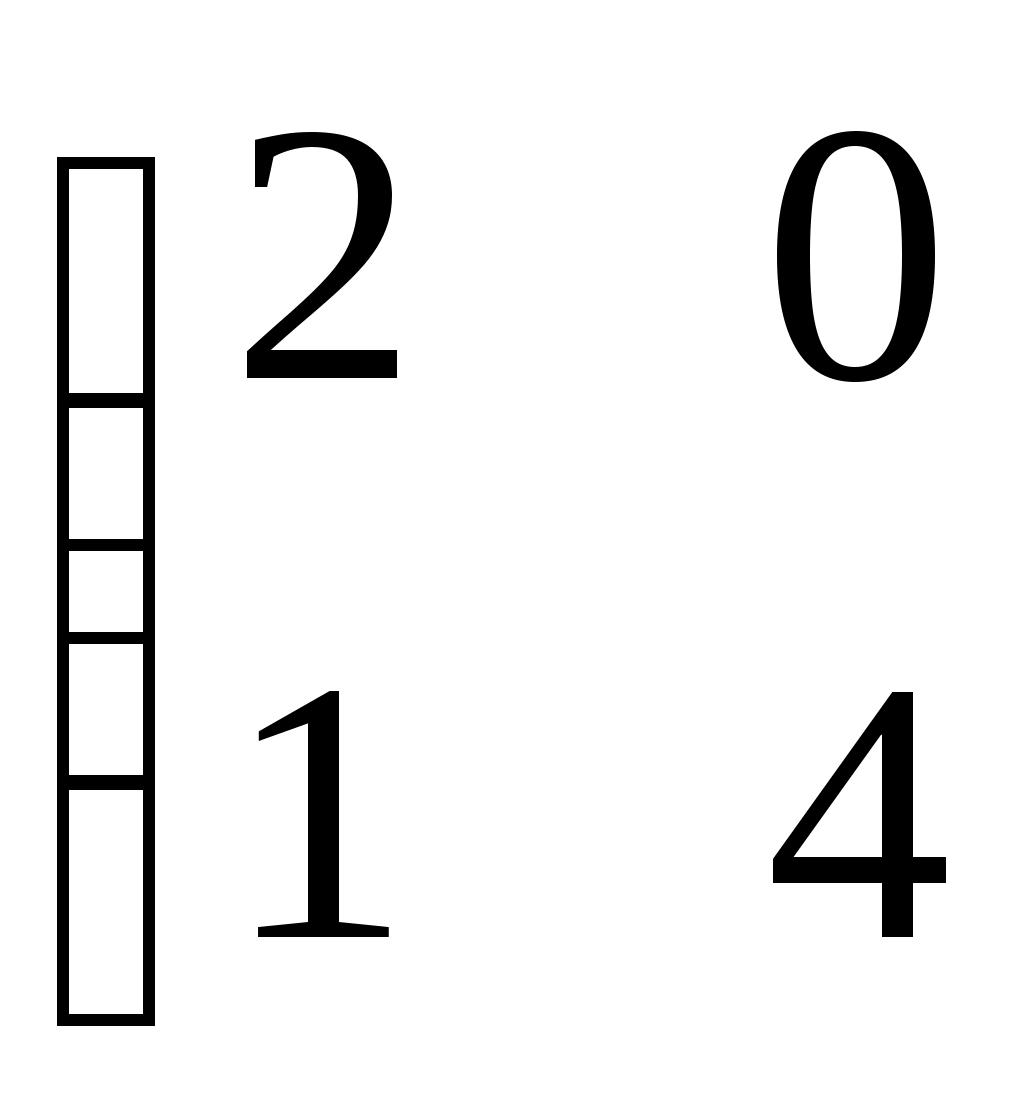 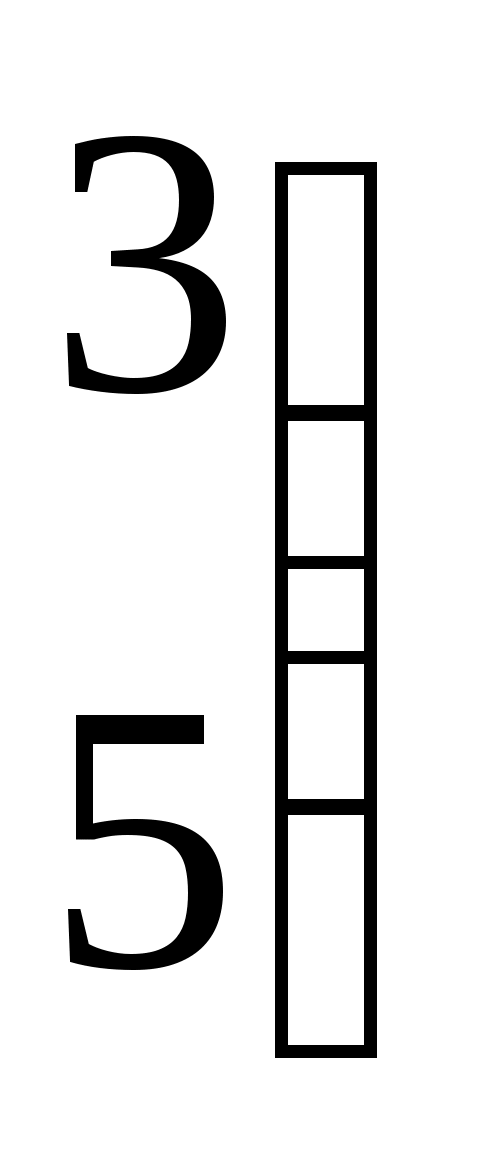 и и 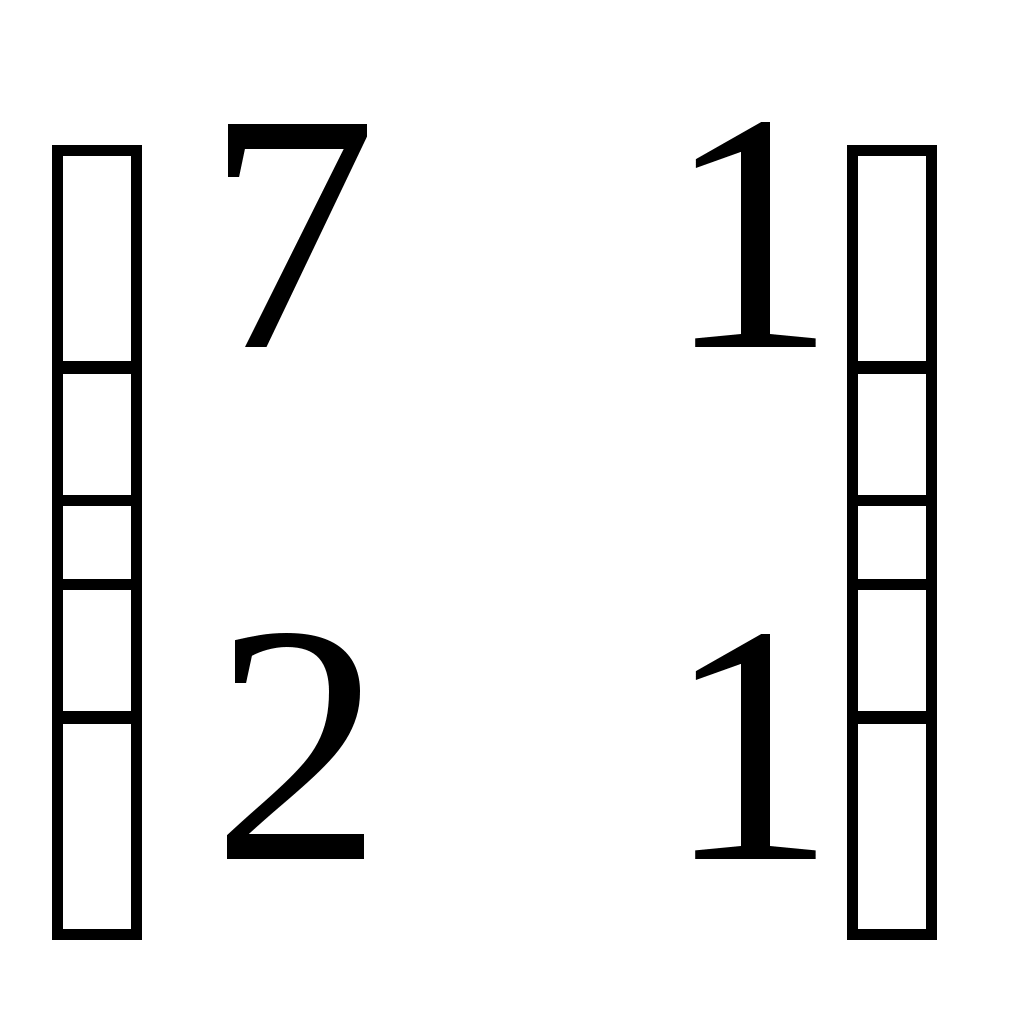 4. 4. 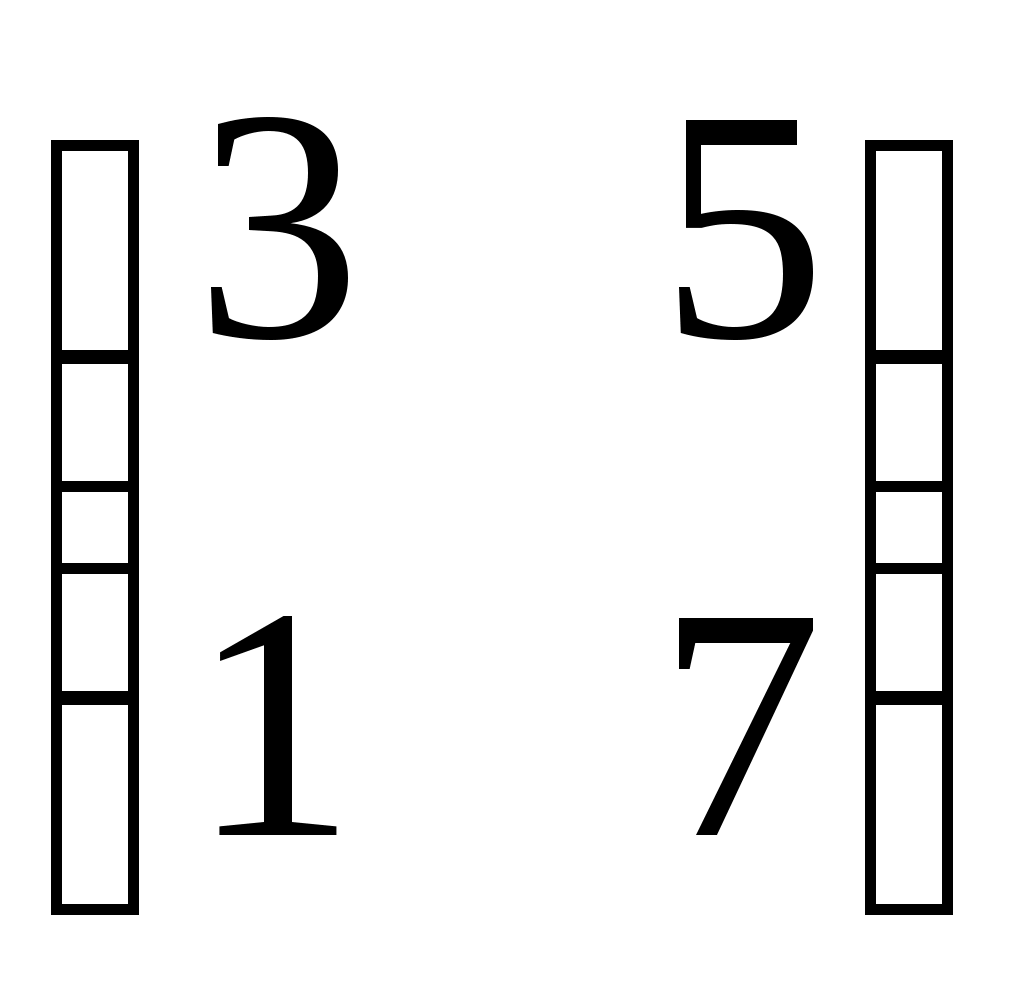 и и 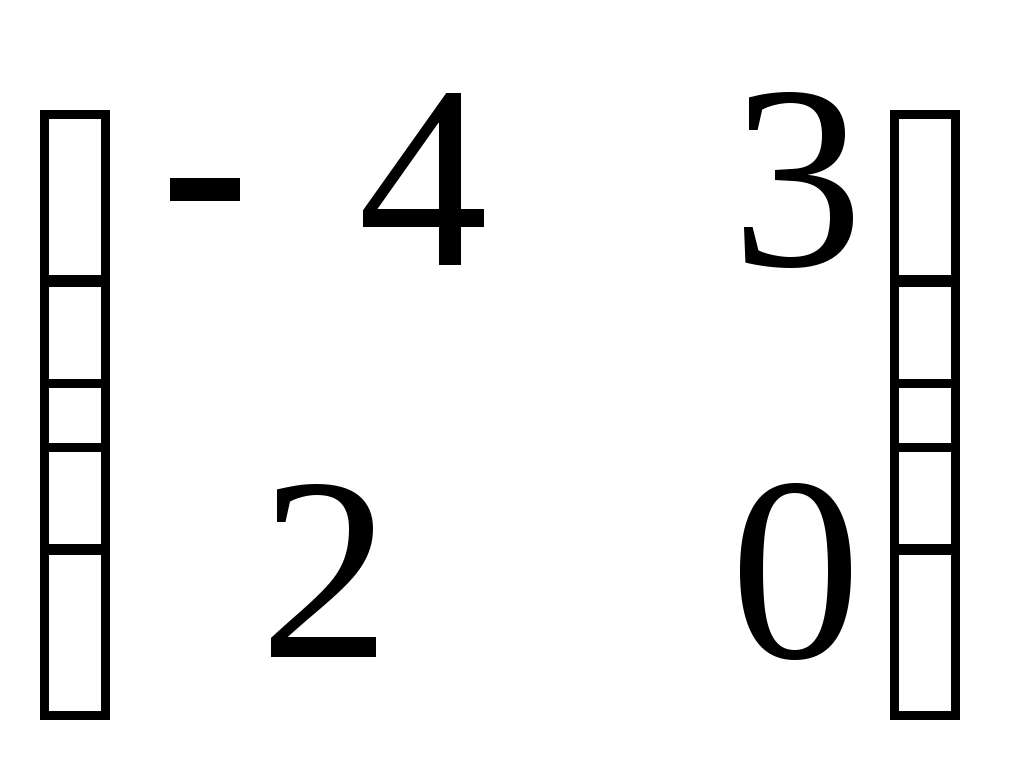
|
| Какую систему нельзя решить по правилу Крамера? | 1. 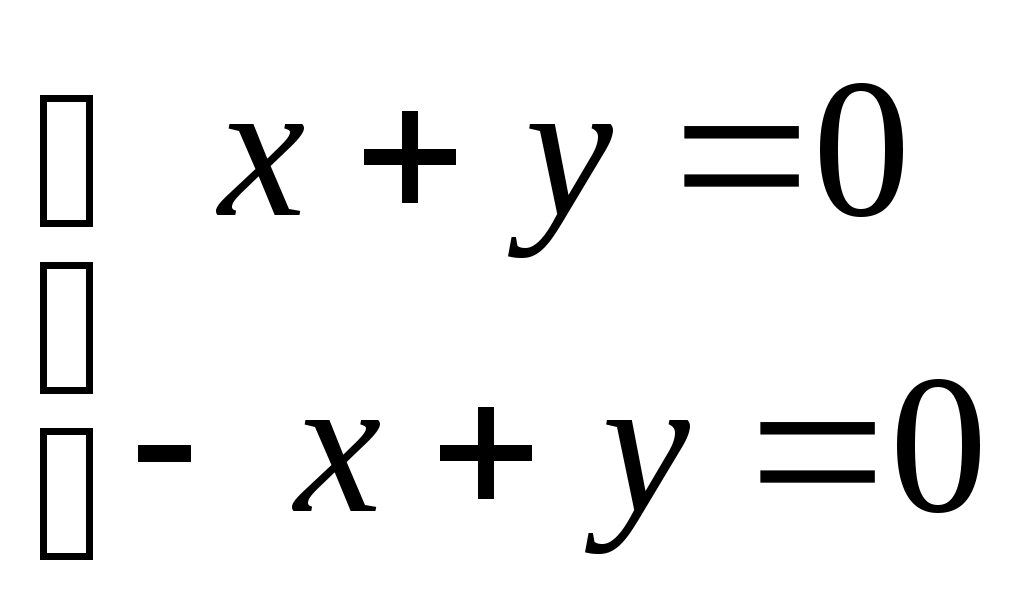 2. 2. 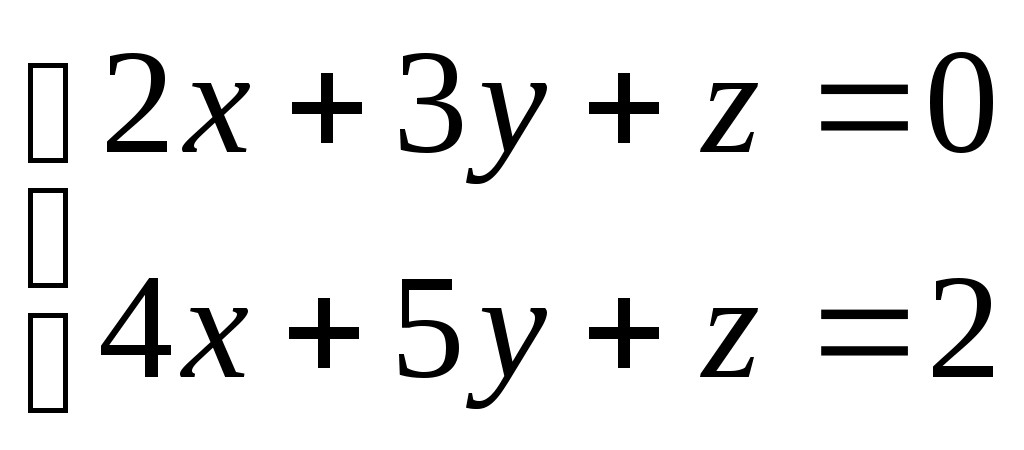
3. 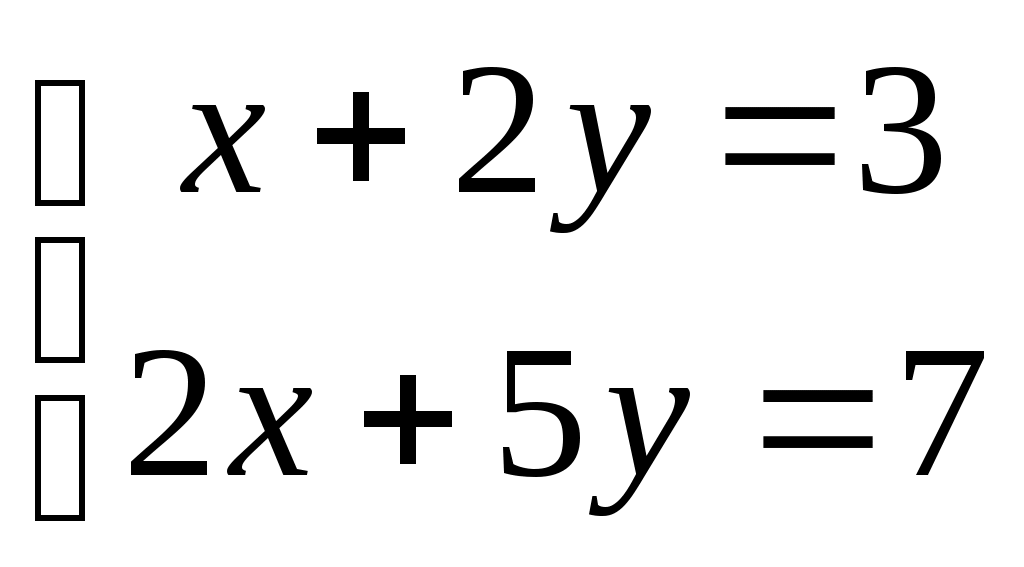 4. 4. 
|
| Какие матрицы являются перестановочными? | 1. 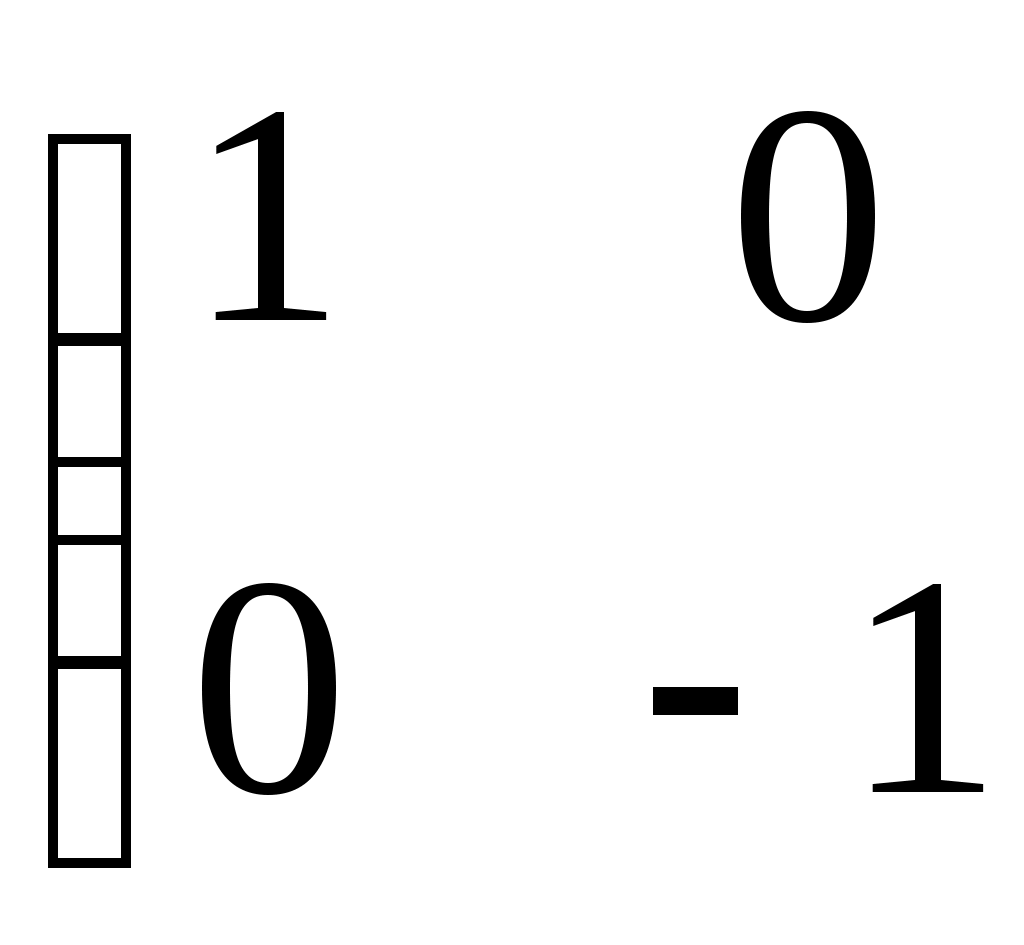 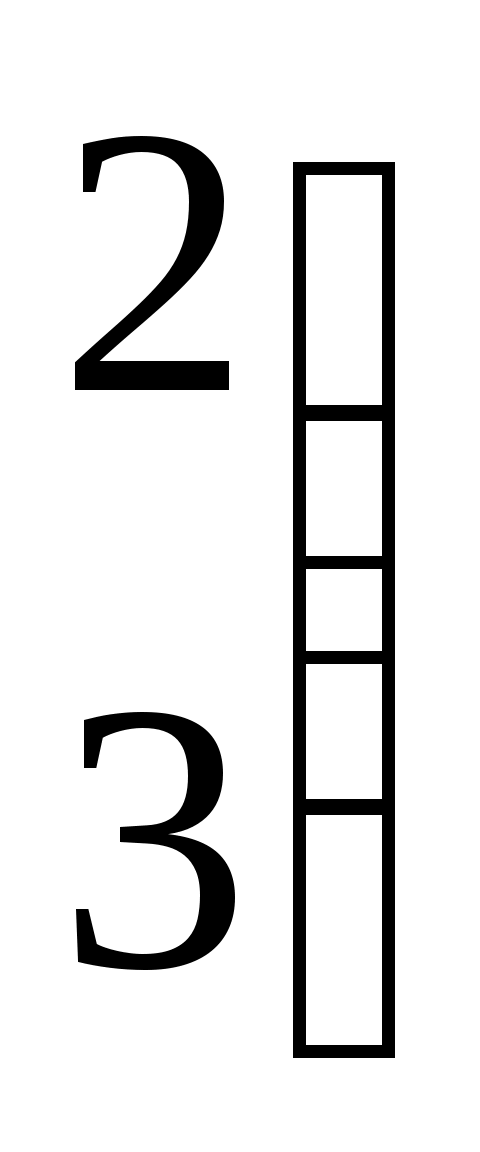 и и 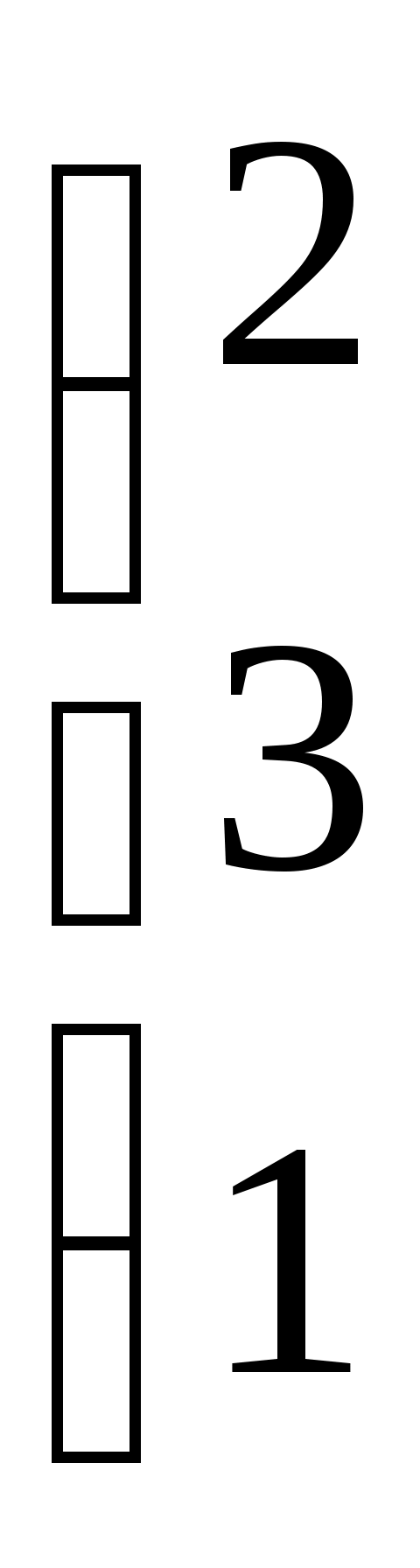 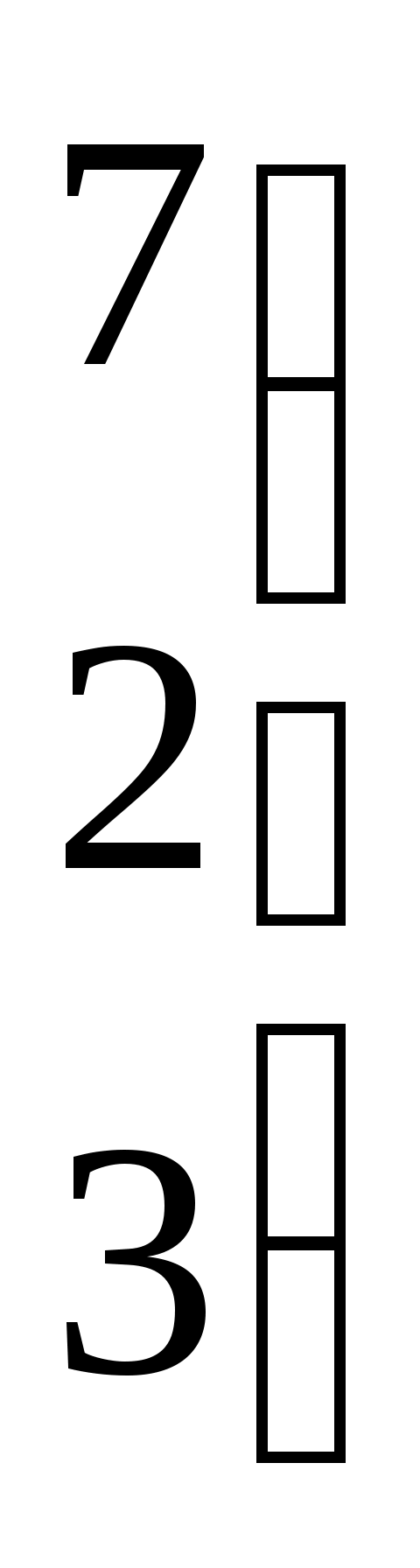 2. 2. 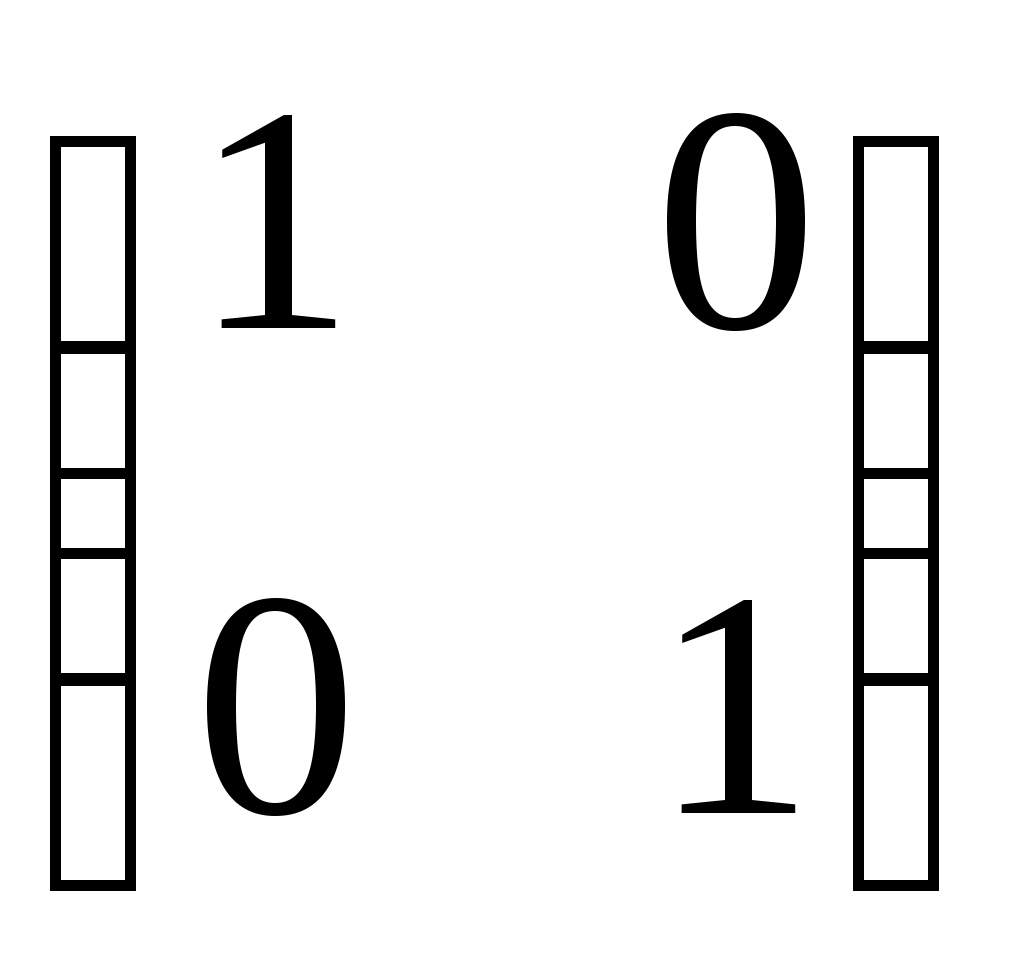 и и 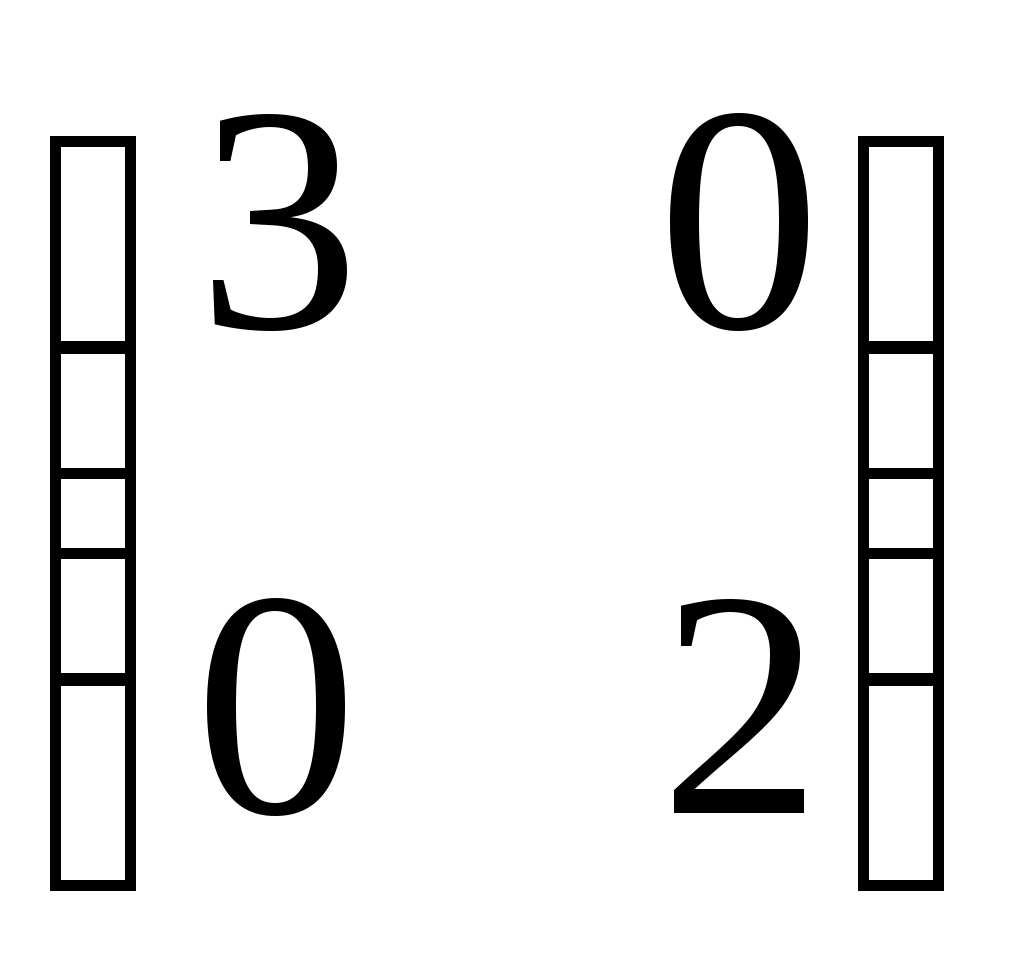
3.  и и 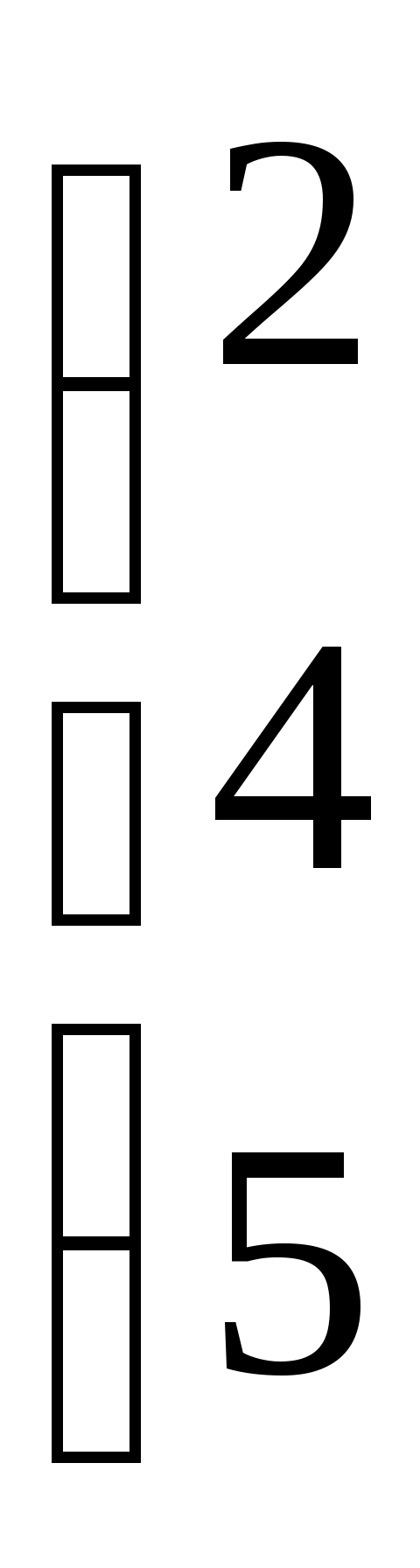 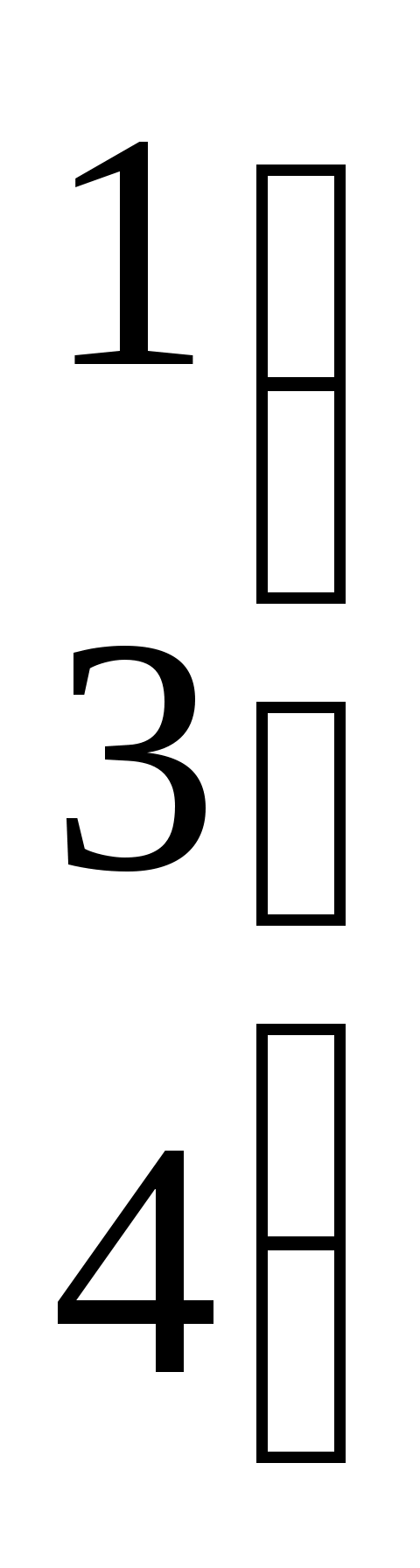 4. 4. 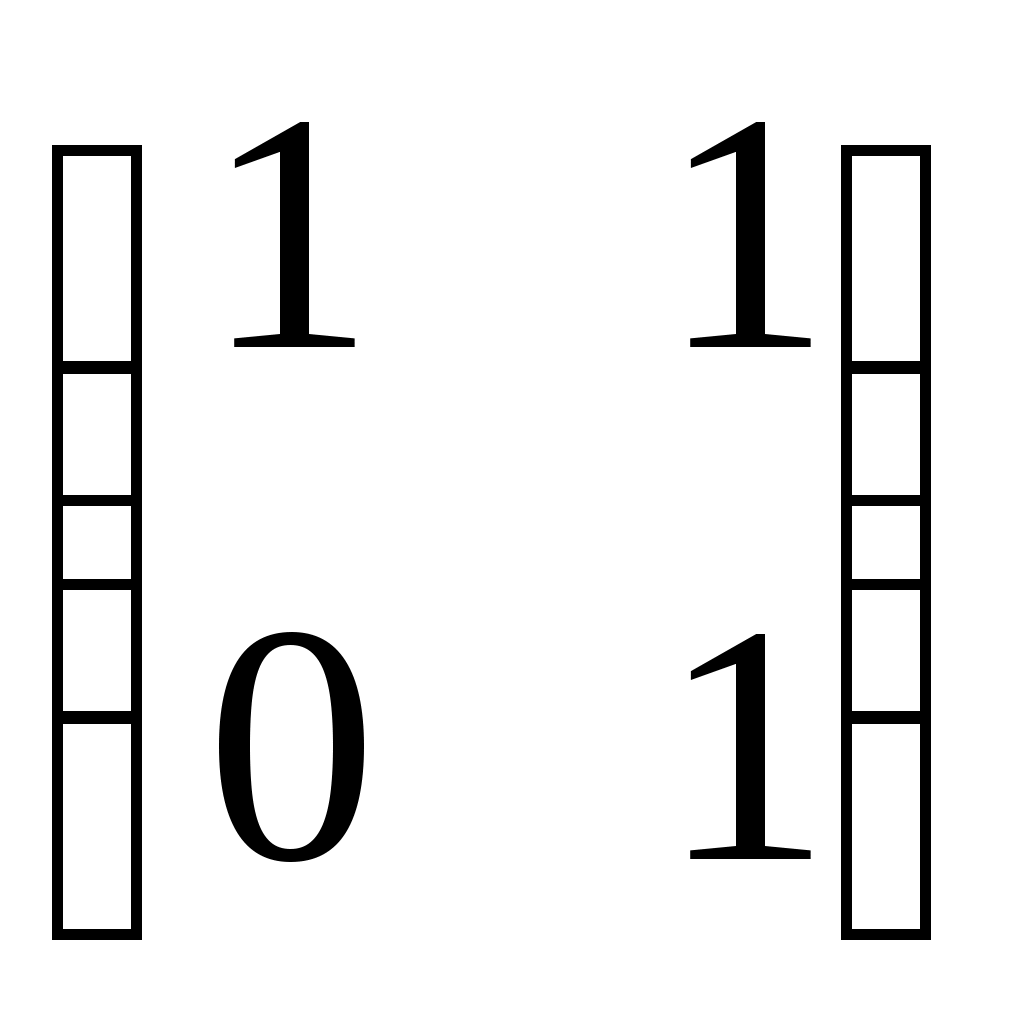 и и 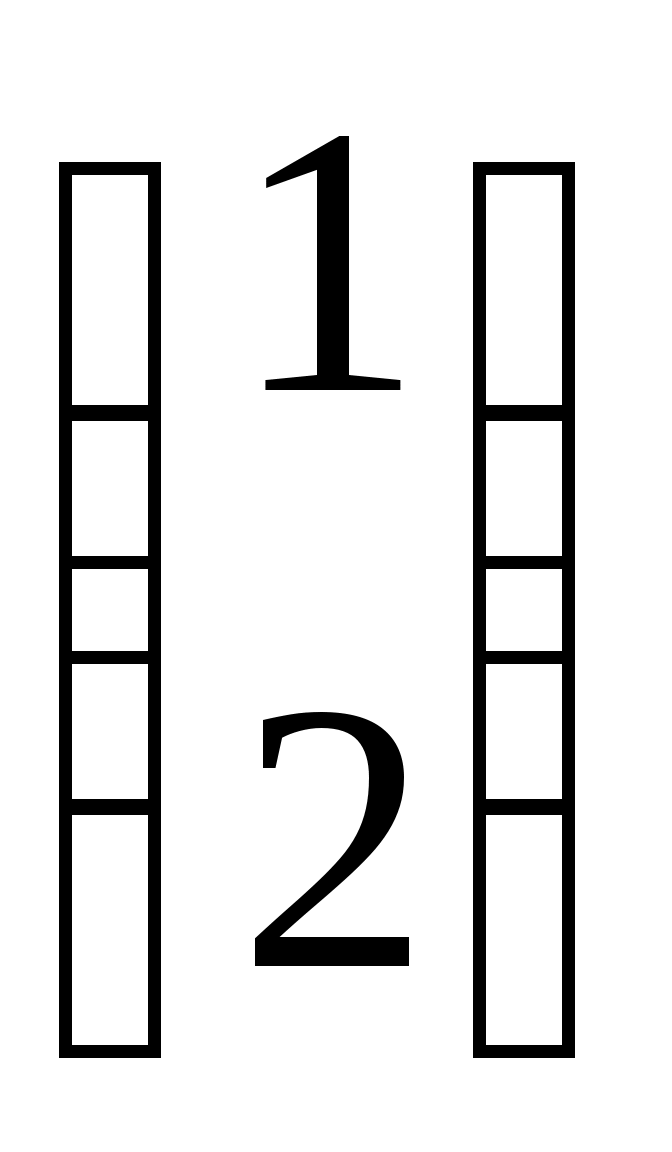
|
| Квадратная матрица называется нижней треугольной, если: |
Все её элементы, находящиеся ниже главной диагонали, равны 0
в ней количество строк превосходит количество столбцов
Все её элементы, находящиеся выше главной диагонали, равны 0
в ней количество столбцов превосходит количество строк
|
|
При решении системы 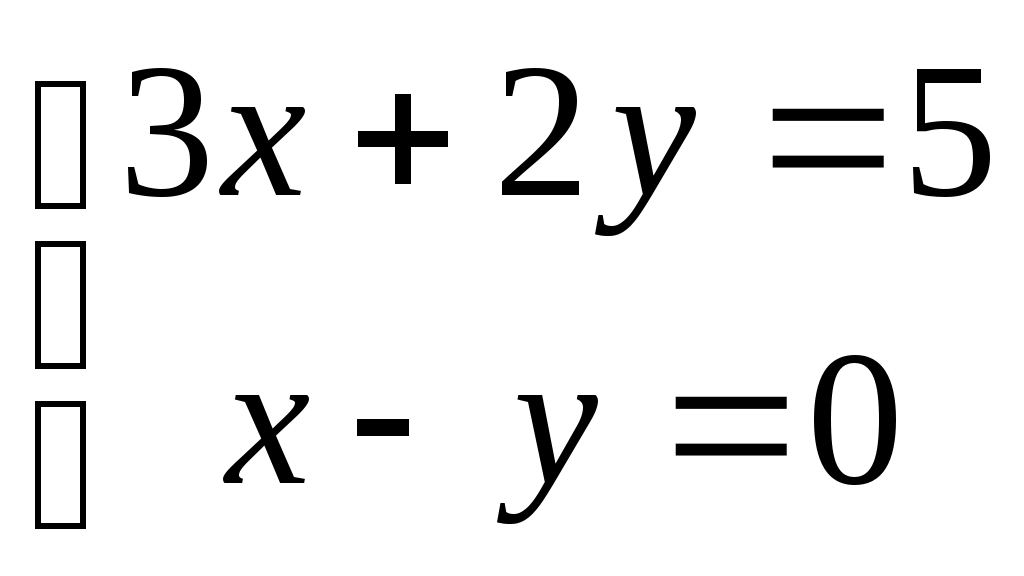 по правилу Крамера определитель системы по правилу Крамера определитель системы 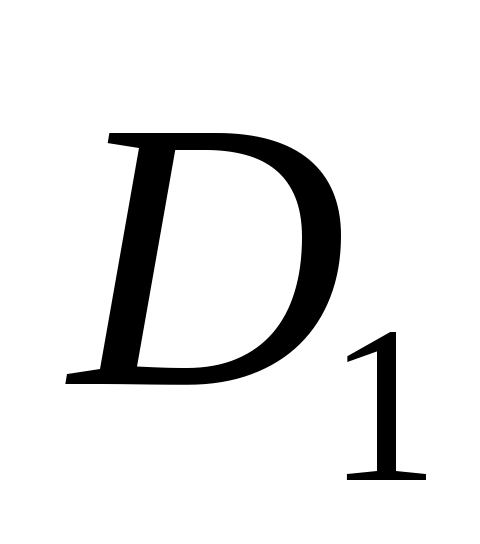 , с помощью которого находится неизвестная x по формуле , с помощью которого находится неизвестная x по формуле 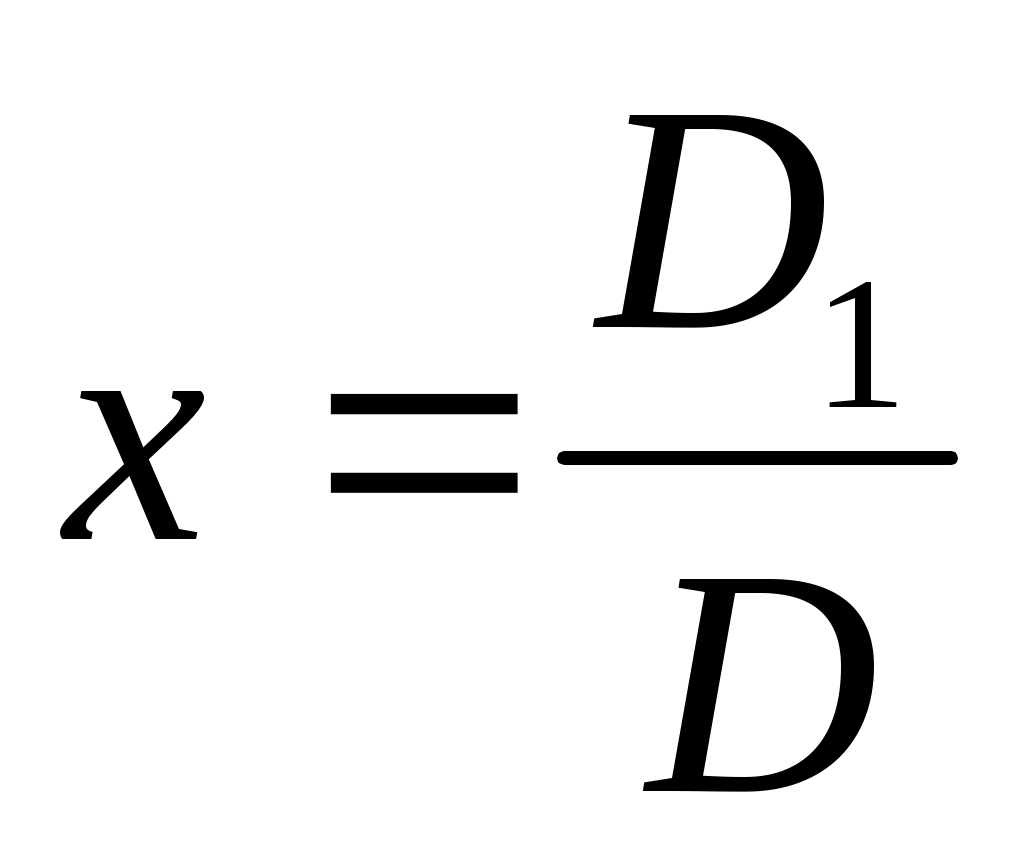 , равен: , равен:
|
1. 2. 2. 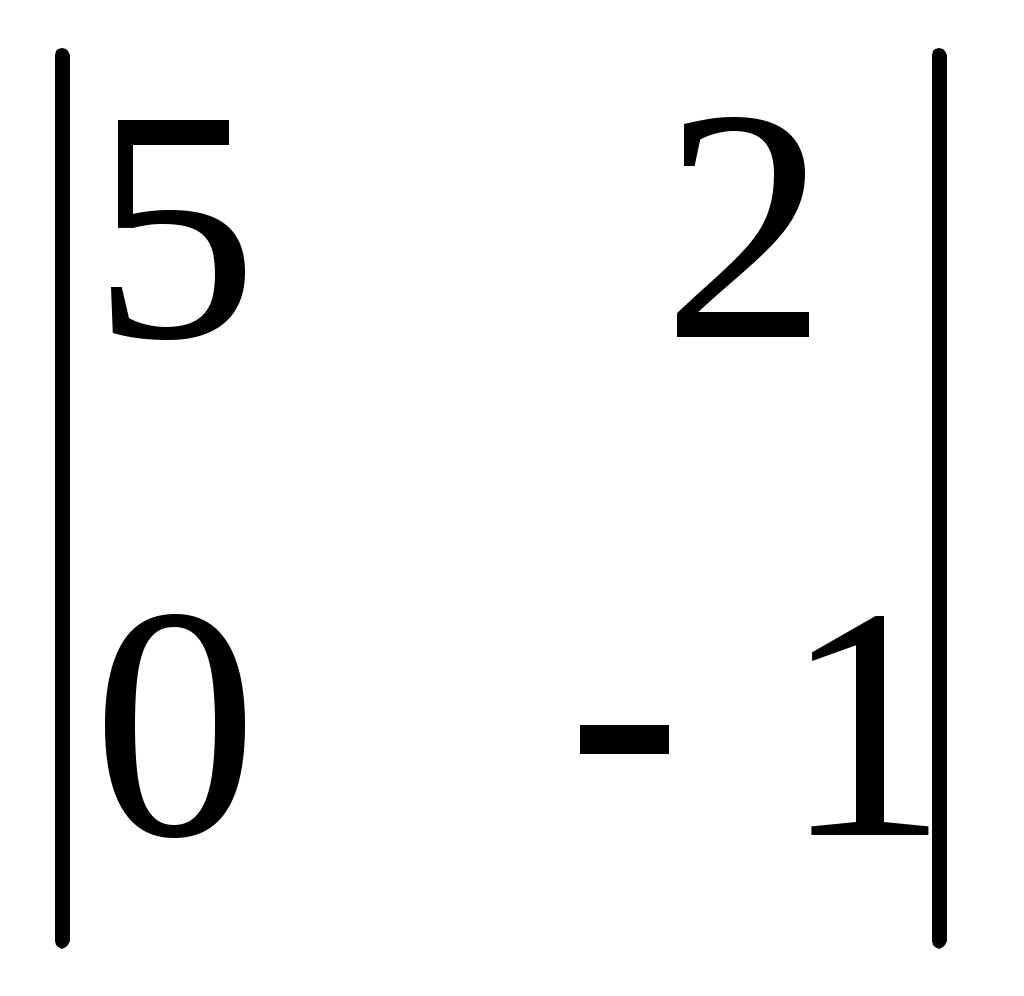 3. 3. 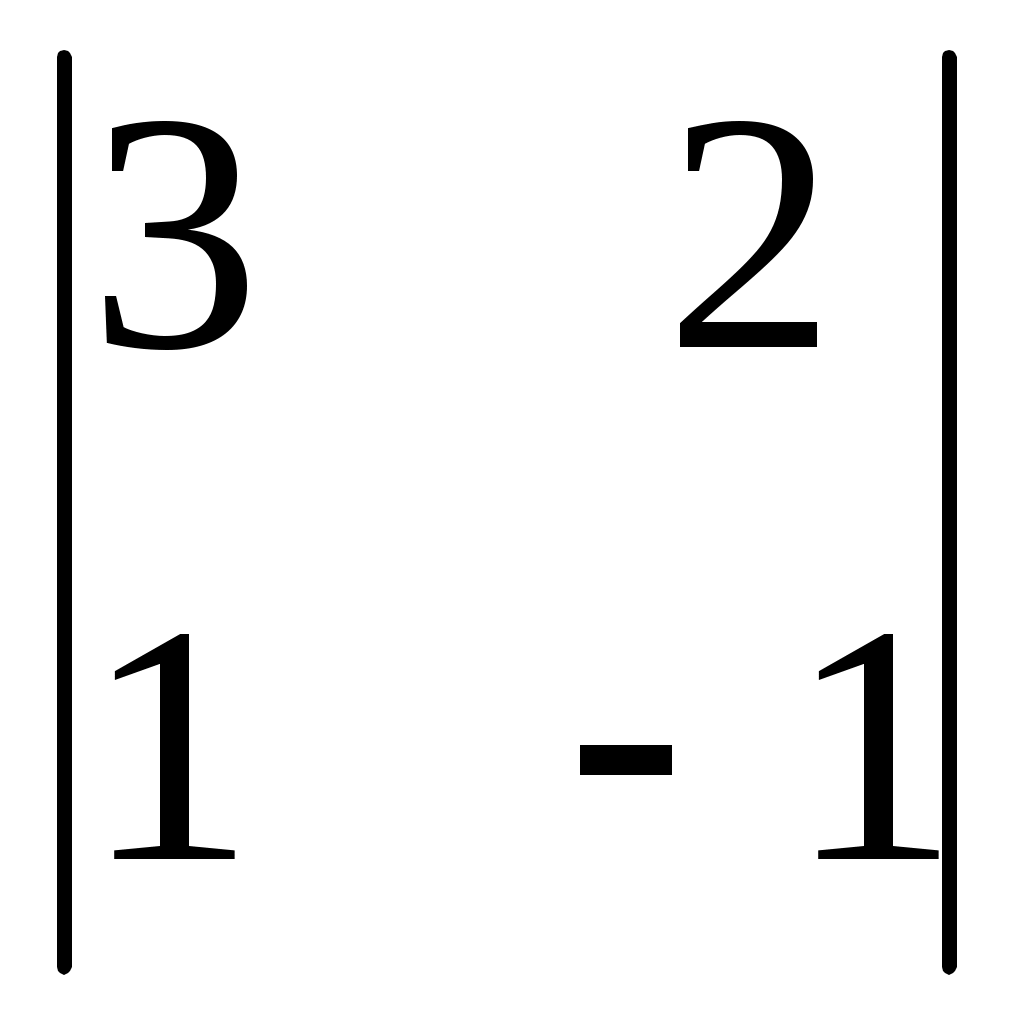
4. 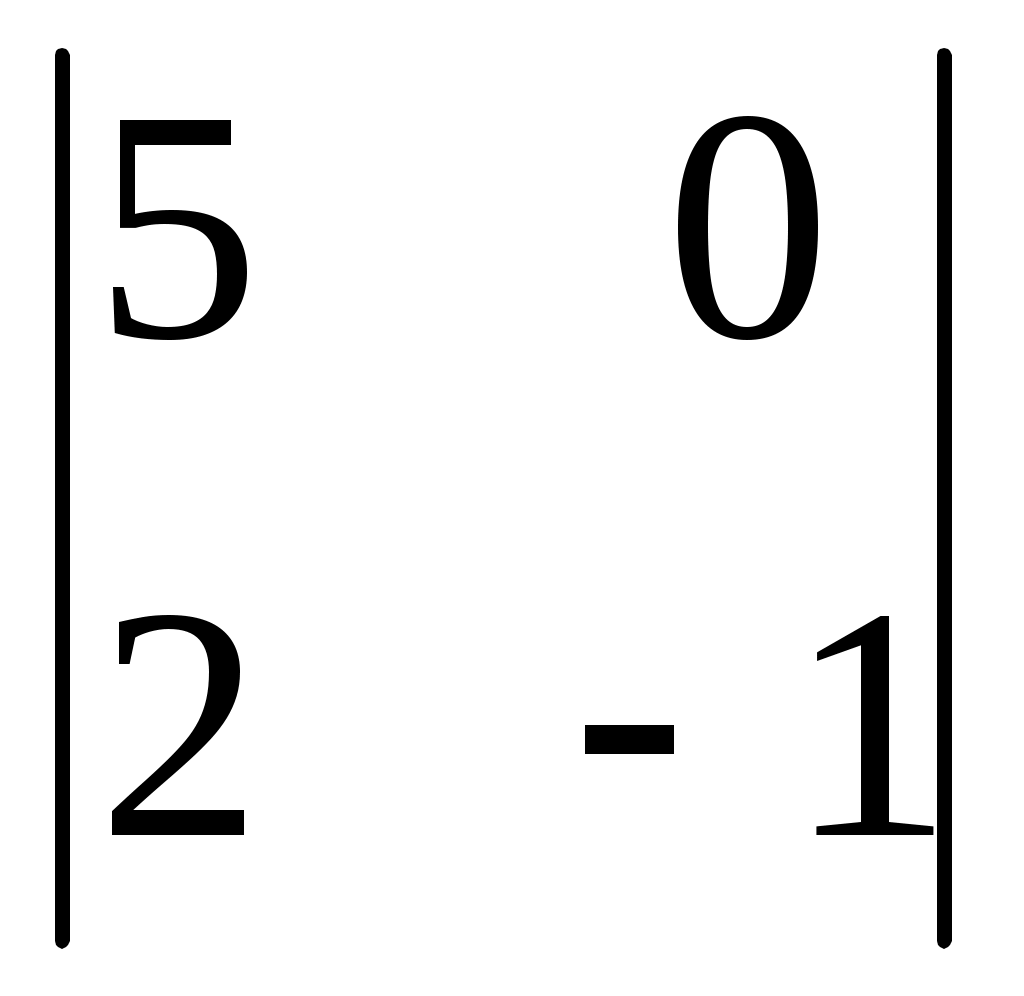
|
|
Элементарными называются такие преобразования матрицы, при которых не изменяется …
|
Исходная матрица
Определитель матрицы
Все миноры матрицы
Ранг матрицы
|
|
Матрица называется нулевой, если
|
1. она имеет одну нулевую строку
2.Все её элементы, стоящие на главной диагонали, равны 0
3. Все её элементы равны 0
4.она имеет по крайней мере одну нулевую строку
|
|
Если в квадратной матрице к элементам второй строки прибавить соответствующие элементы первой строки, умноженные на 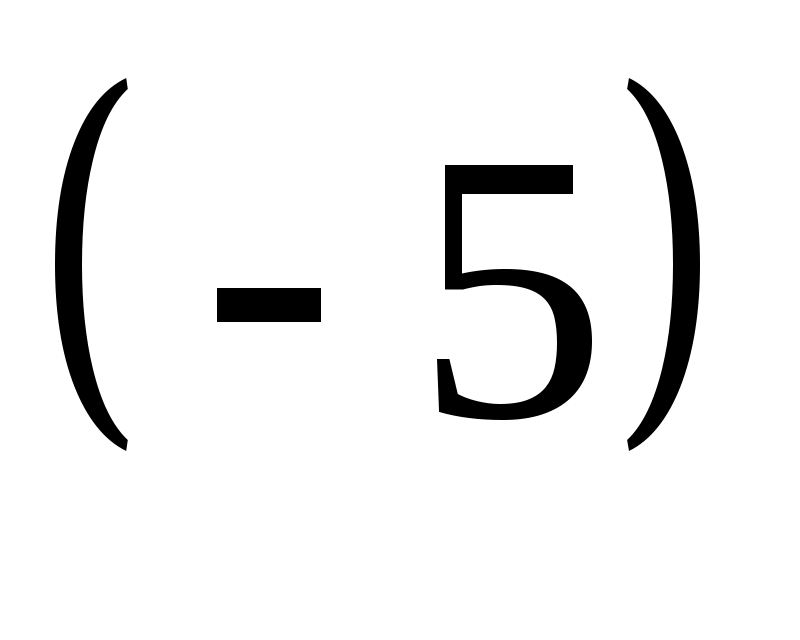 , ,
то её определитель . . .
|
1. поменяет знак 2.увеличится в 5 раз
3. умножится на 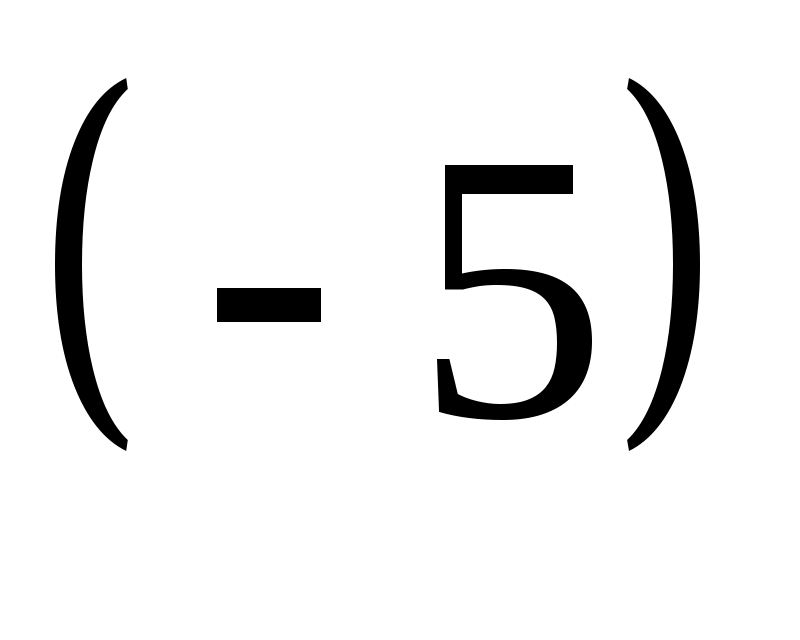
4. не изменится
|
| Что называется минором элемента  определителя третьего порядка? определителя третьего порядка? |
элемент  , умноженный на , умноженный на 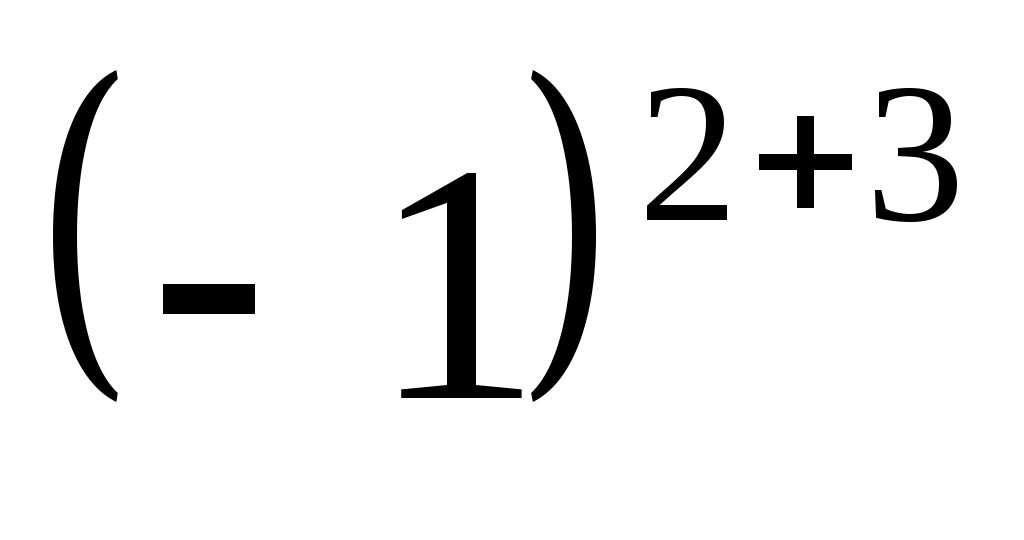
определитель второго порядка, полученный из исходного определителя в результате вычёркивания второй строки и третьего столбца
определитель второго порядка, полученный из исходного определителя в результате вычёркивания второй строки и третьего столбца, умноженный на 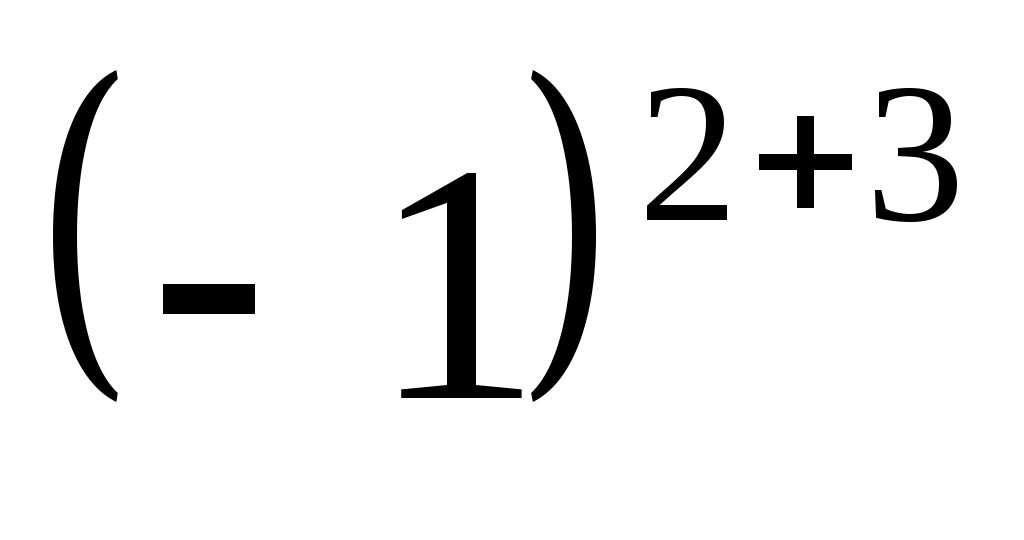
такого понятия не существует
|
| Какую систему нельзя решить матричным методом? | 1. 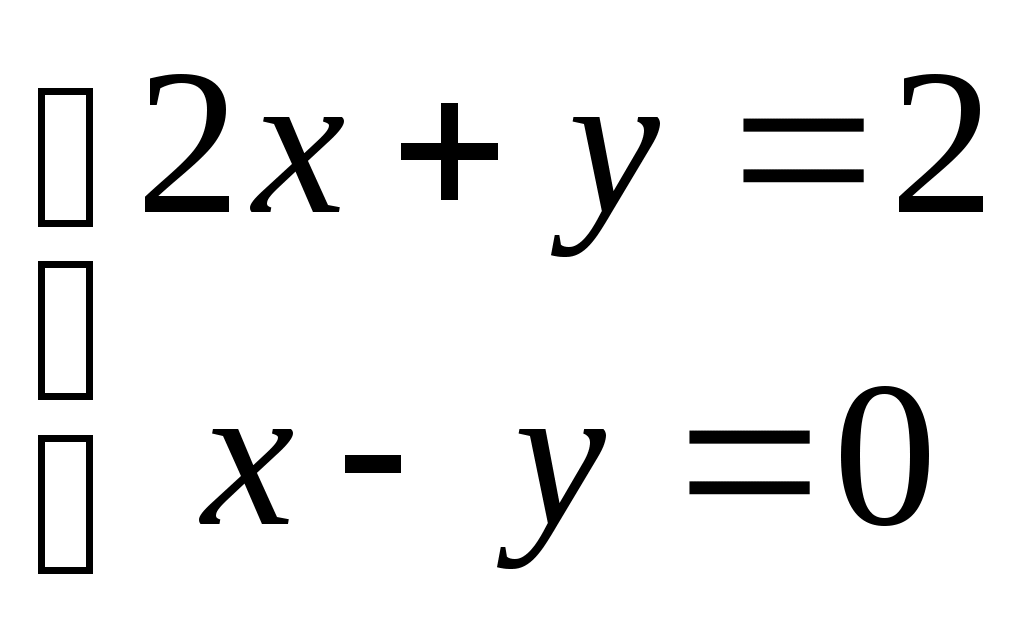 2. 2. 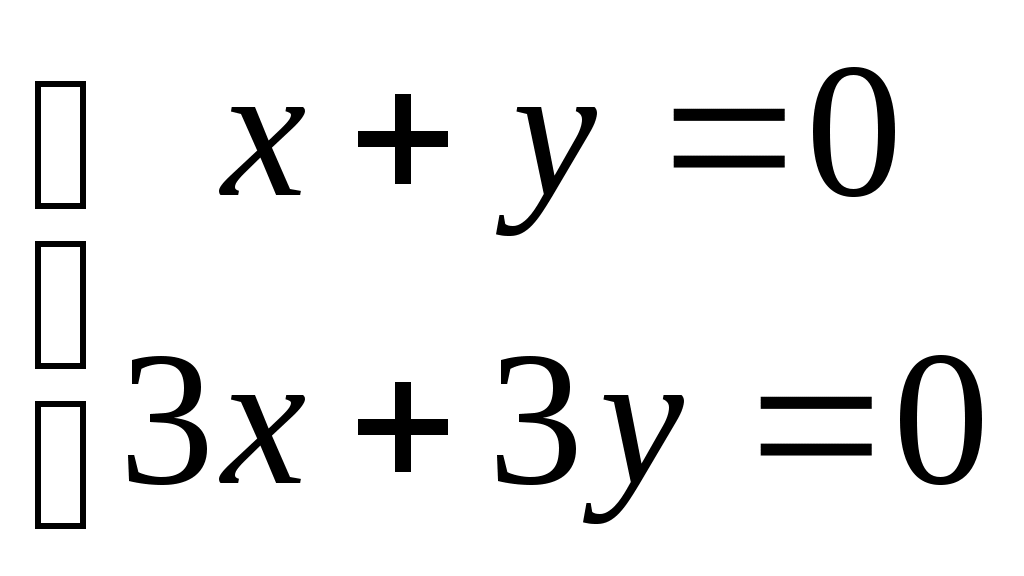
3.  4. 4. 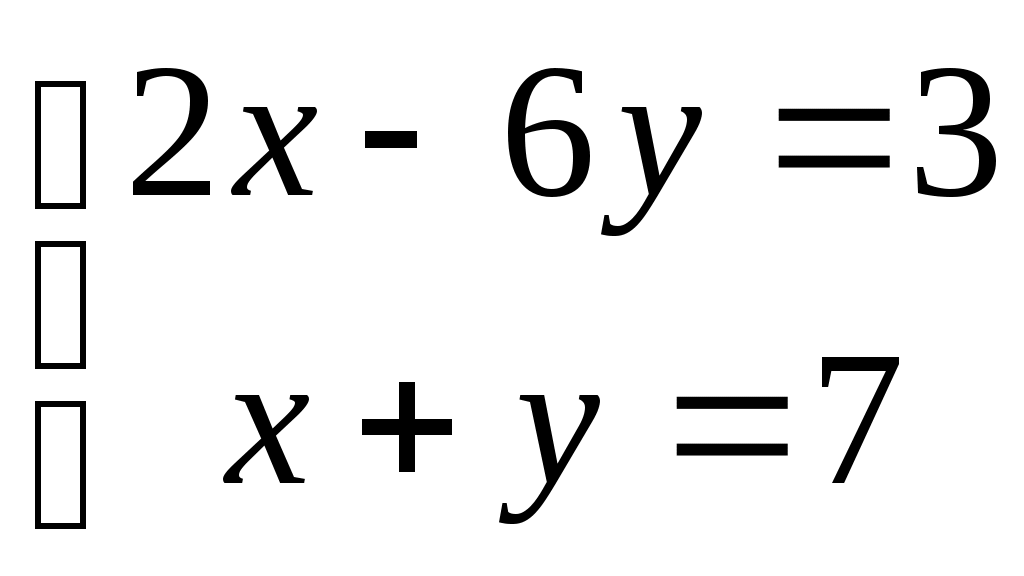
|
| Какая операция определена не для всех матриц? |
1.умножение матрицы на число
2.транспонирование матрицы
3.сложение матриц
4.все операции над матрицами определены для любых матриц
|
|
Матрица А имеет размерность 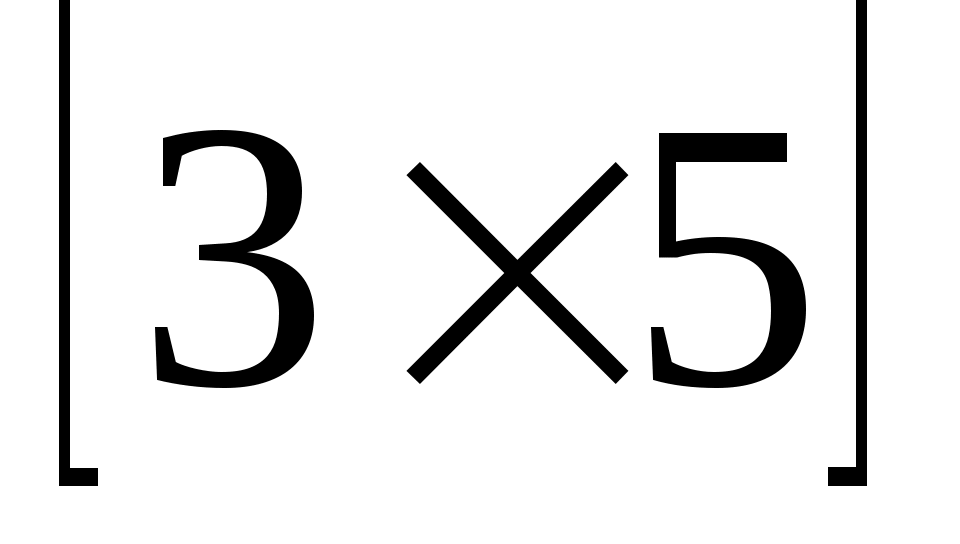 . Какому числу не может равняться ее ранг . Какому числу не может равняться ее ранг 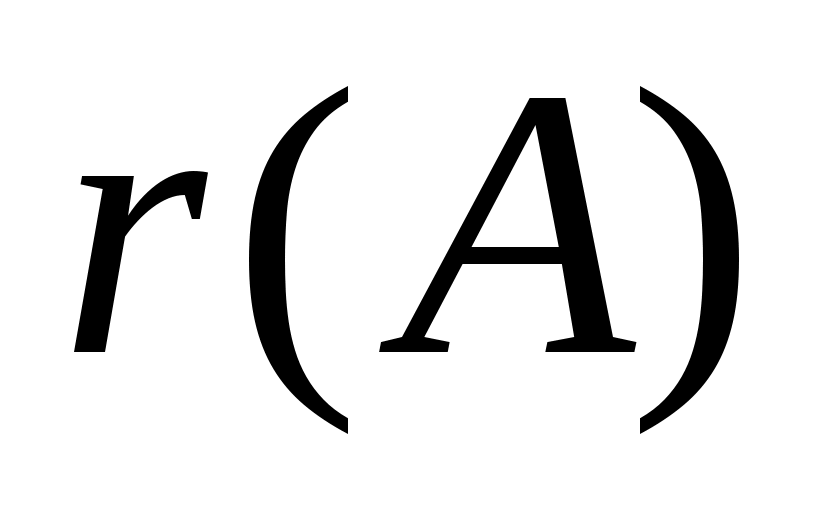 ? ?
|
2
3
0
4
|
|
Матрица A называется симметрической, если
|
1. 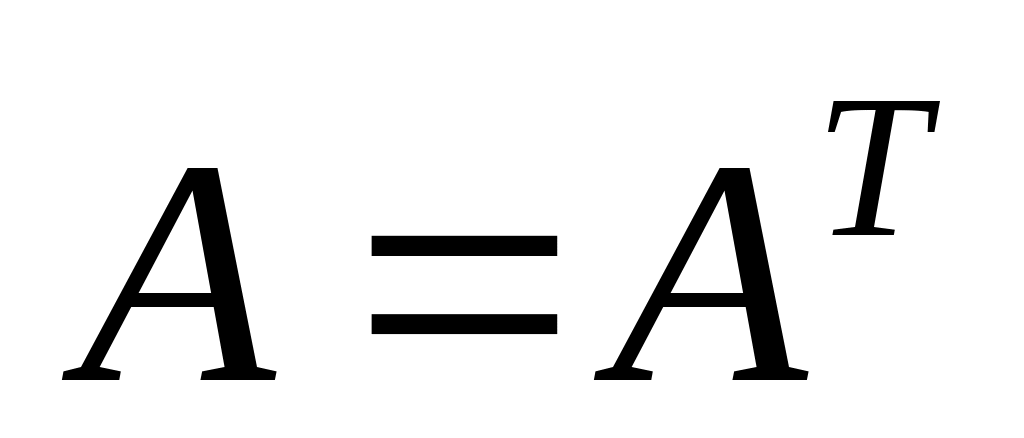 2. 2.  3. 3. 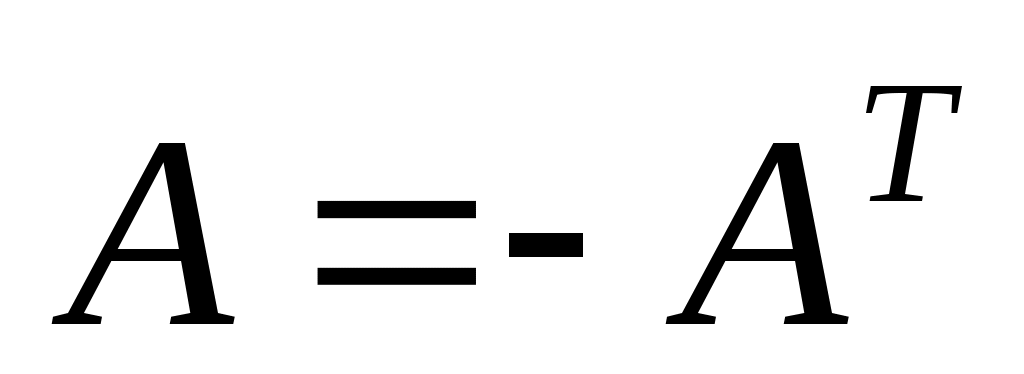 4. 4. 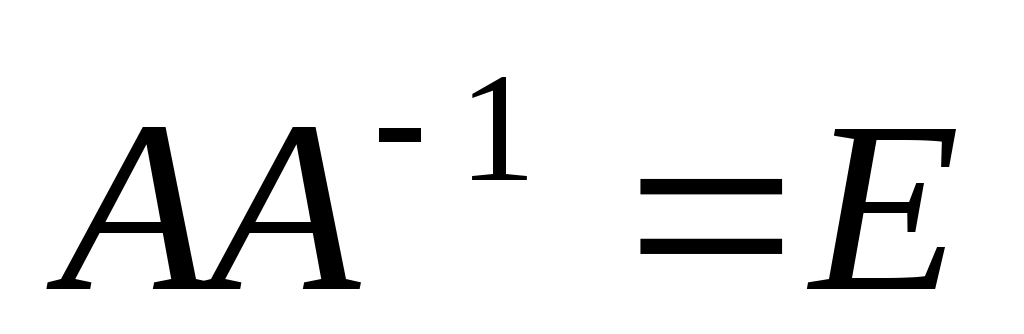
|
|
Какая матрица является противоположной для матрицы  ? ?
|
1. 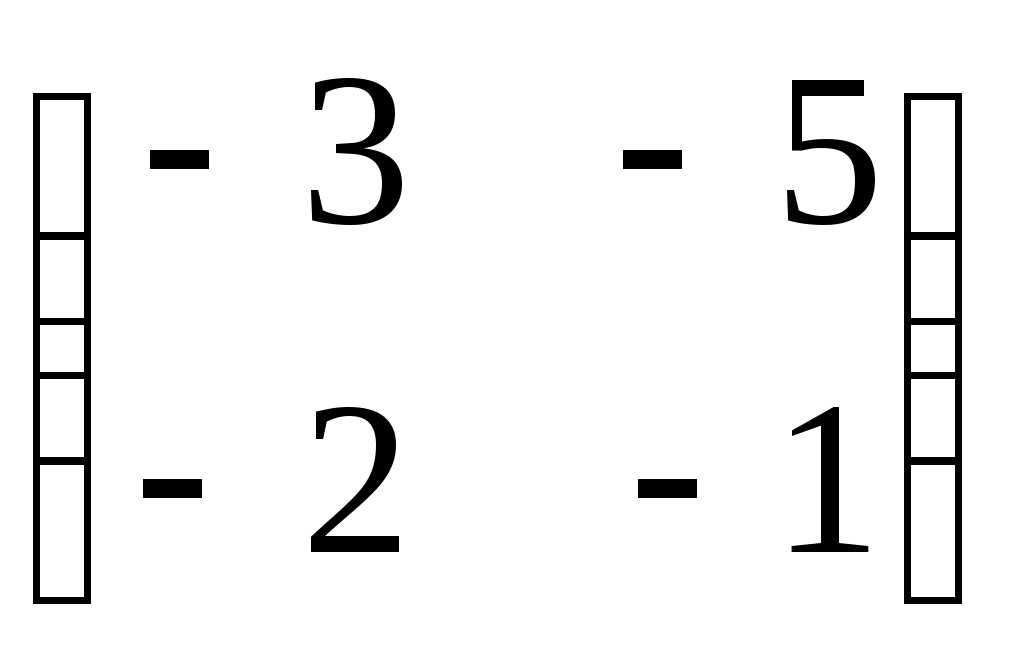 2. 2. 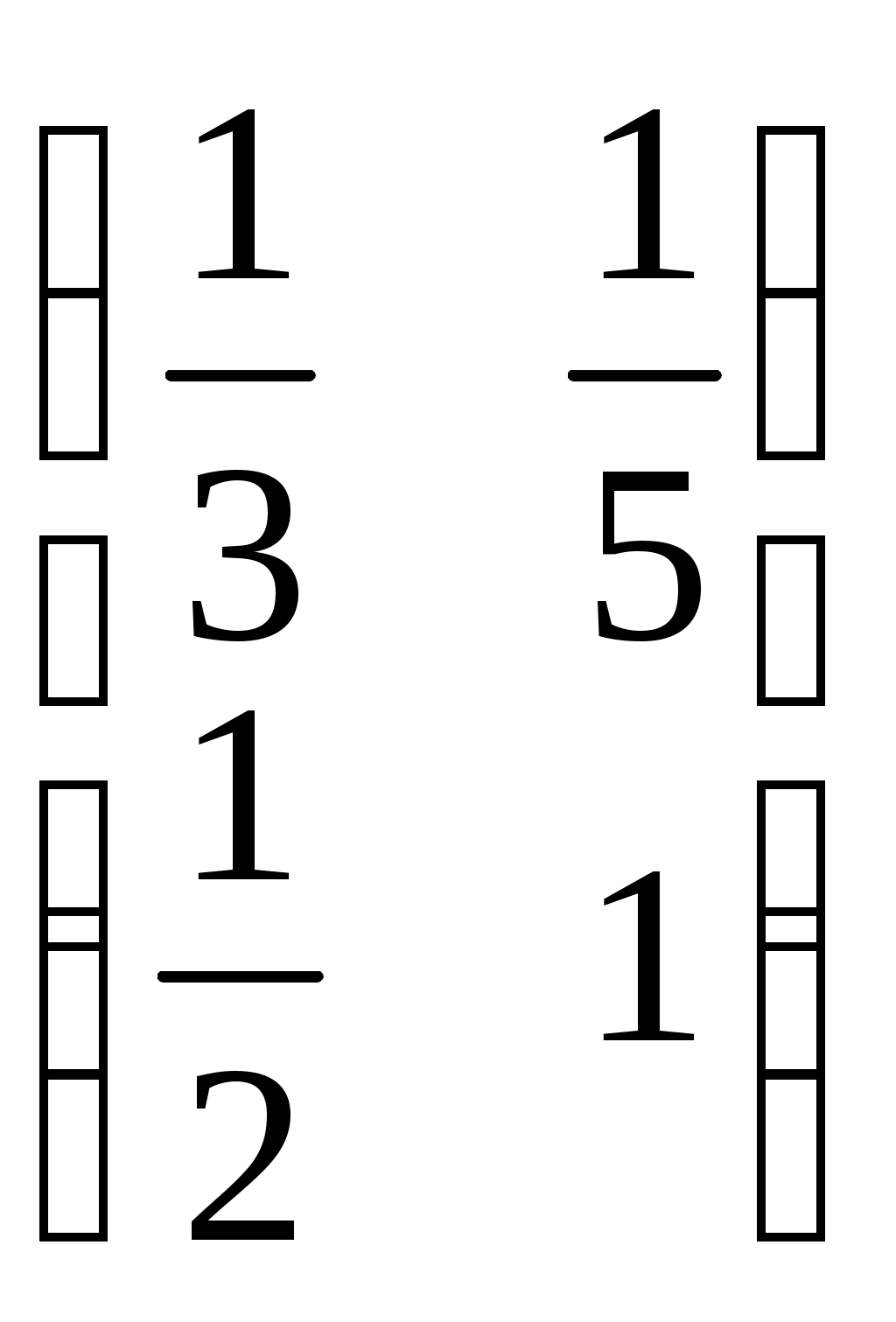 3. 3.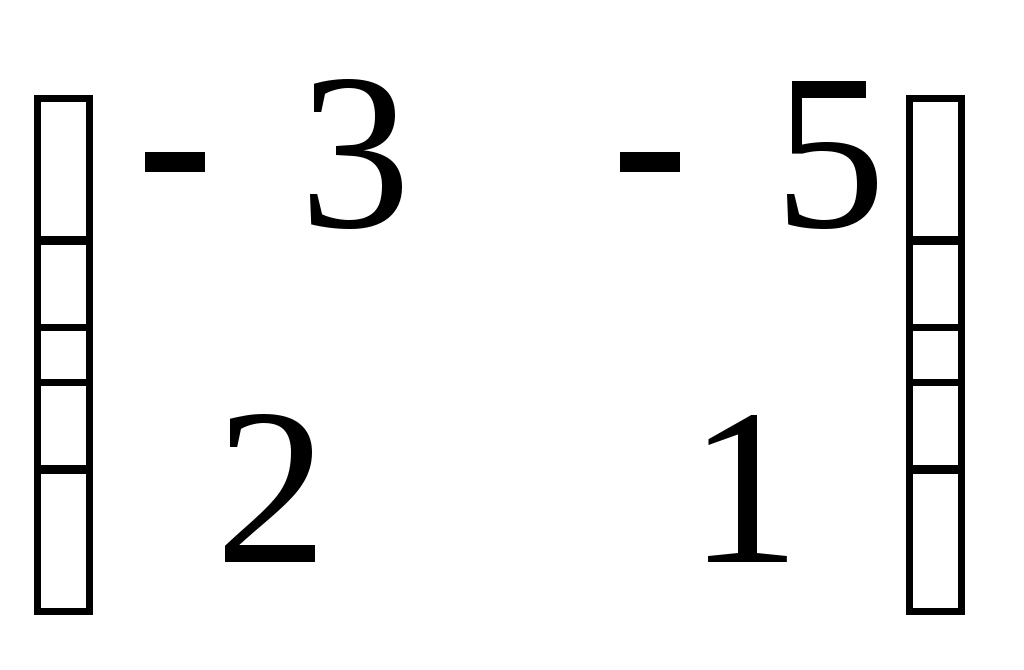
4. 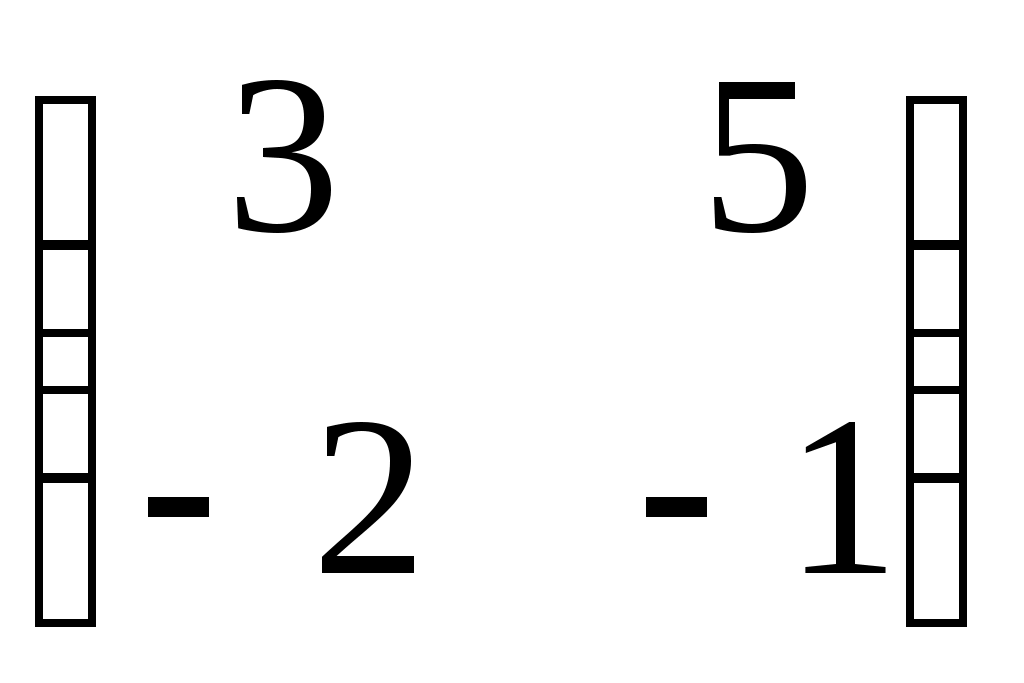
|
|
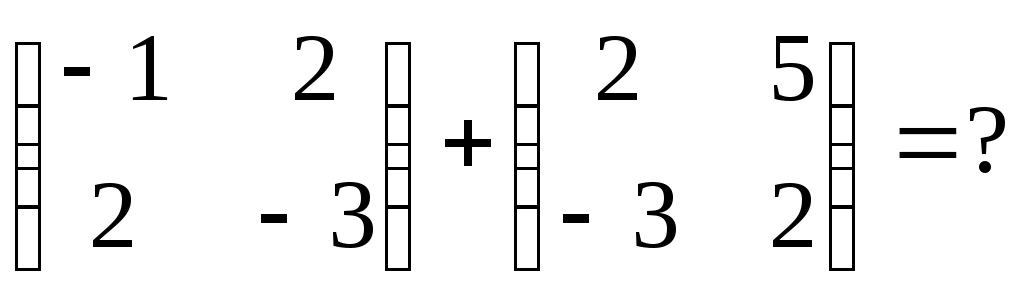
|
1. 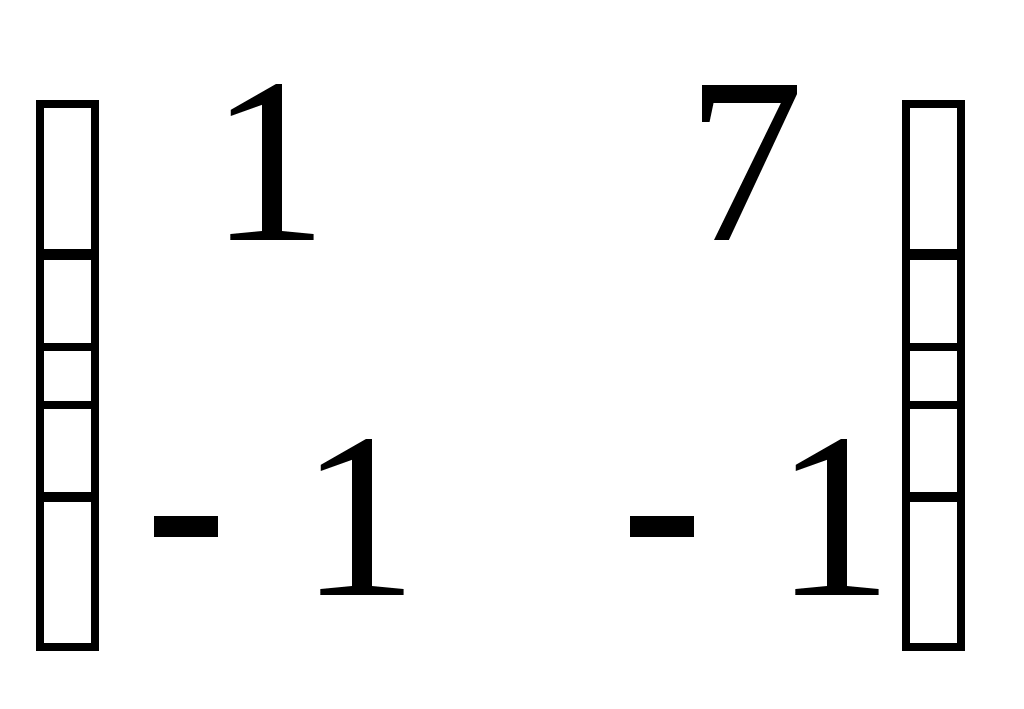 2. 2. 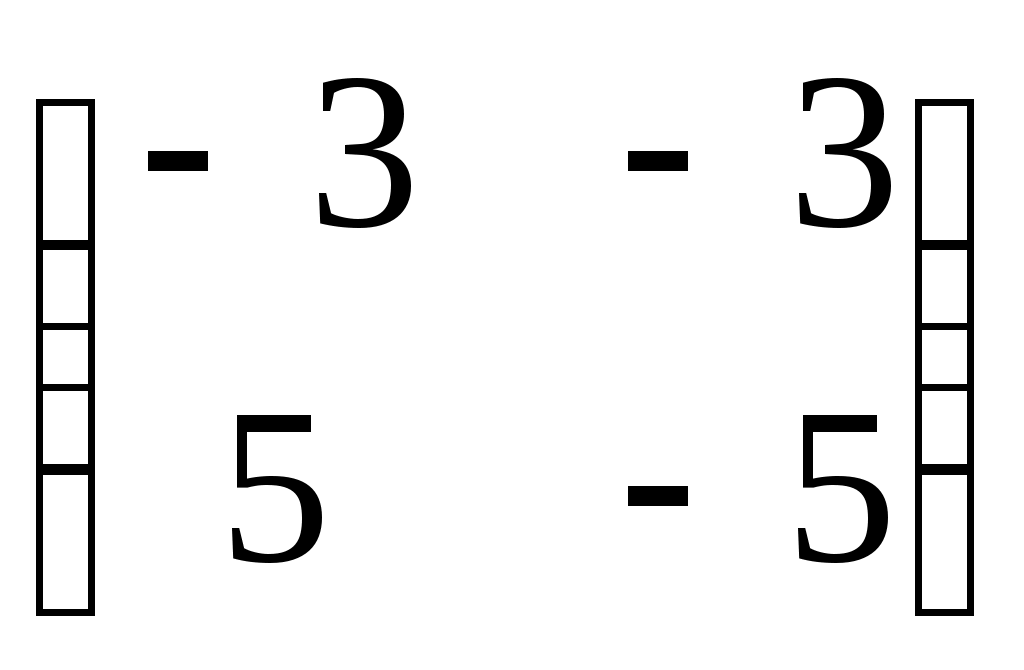 3. 3. 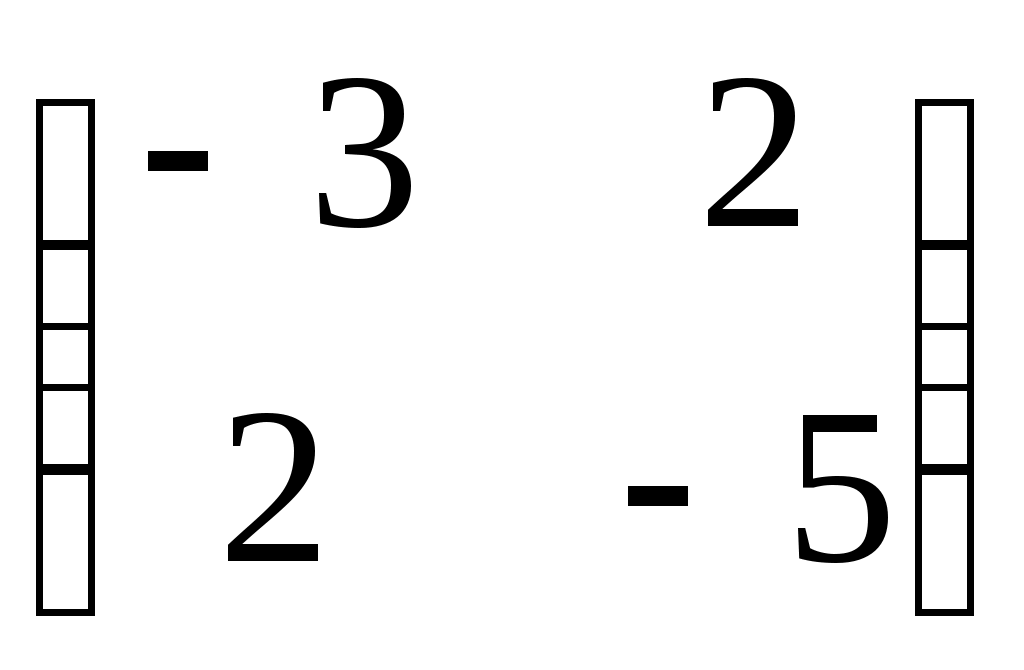 4. 4. 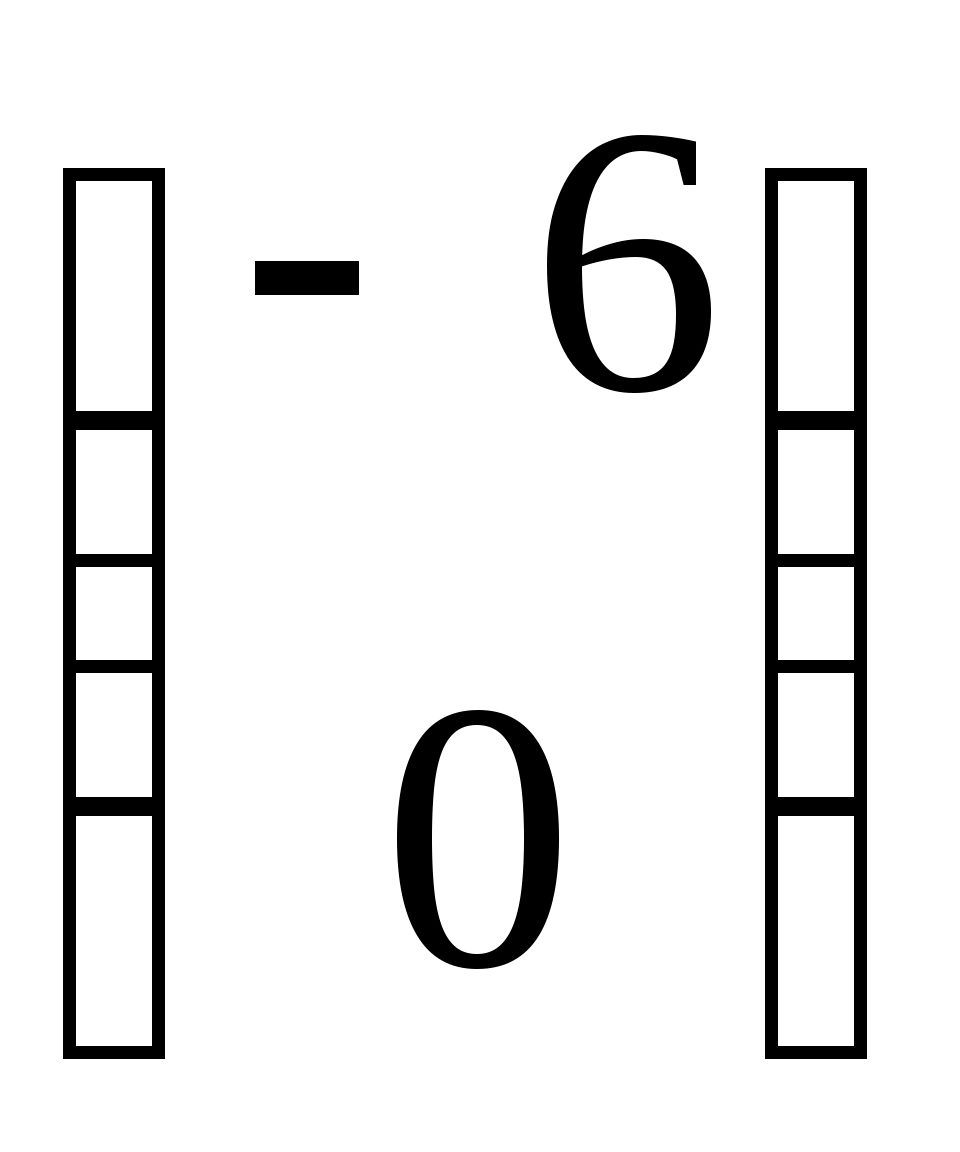
|
|
Вычислить алгебраическое дополнение элемента  в определителе в определителе 
|
1. 8 2. 1 3. 23 4. 12
|
|
Какую матрицу нельзя транспонировать?
|
1.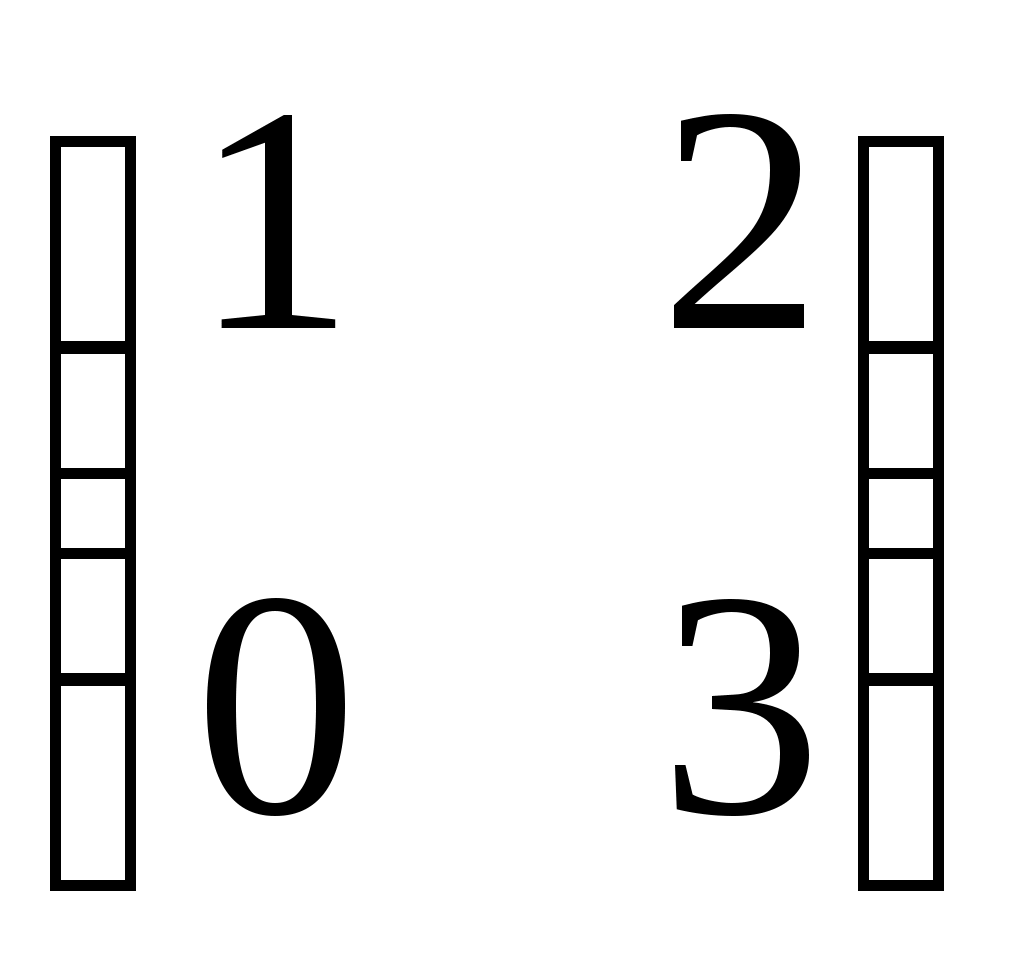 2. 2. 3. 3. 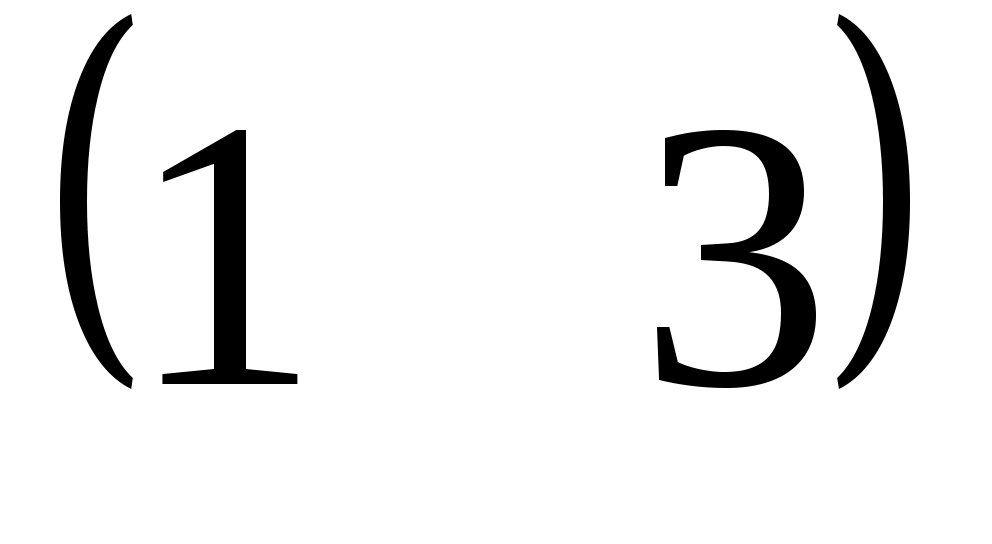
4. любую матрицу можно транспонировать
|
|
Матрицы А и В называются перестановочными, если.…
|
1. 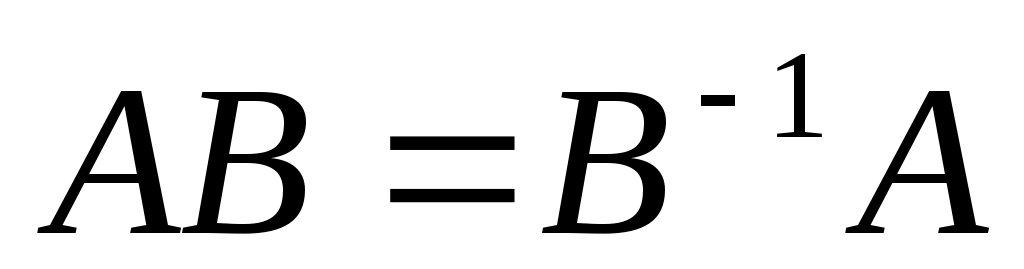 2. 2. 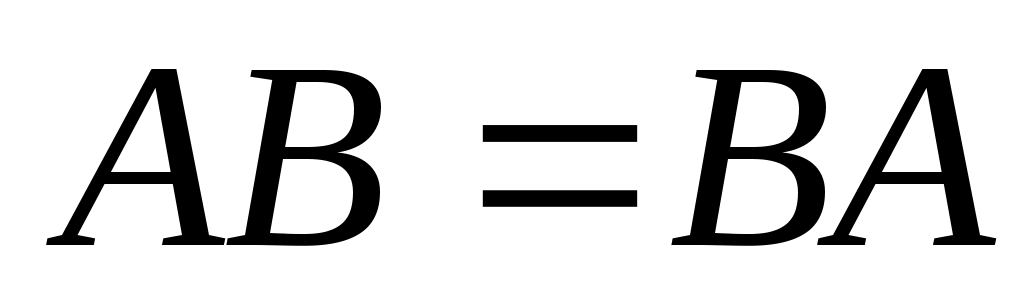 3. 3.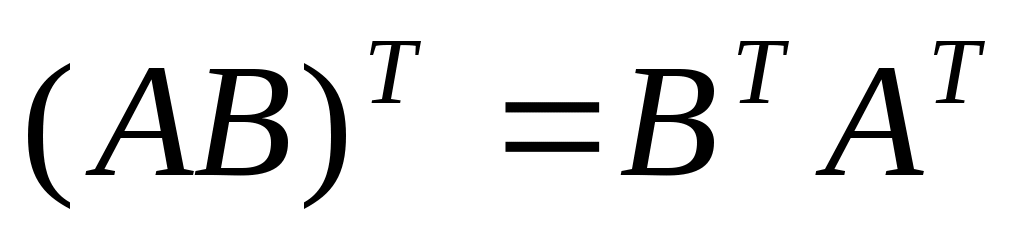
4. 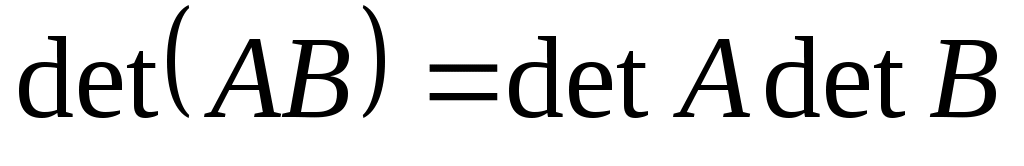
|
|
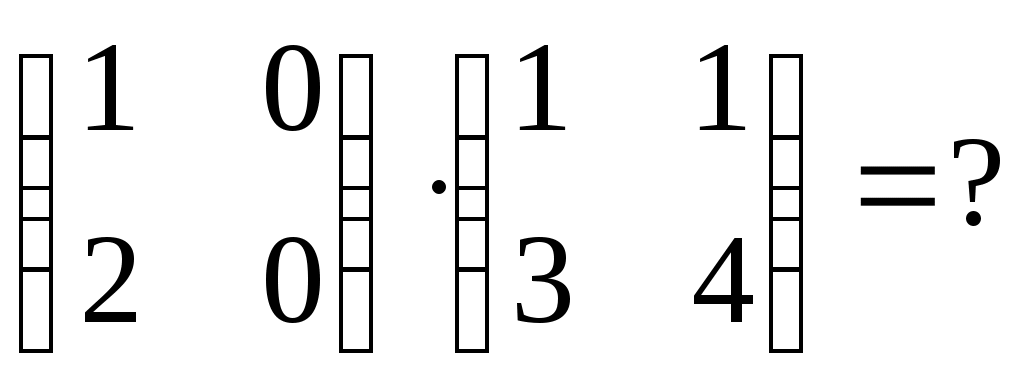
|
1.  2. 2. 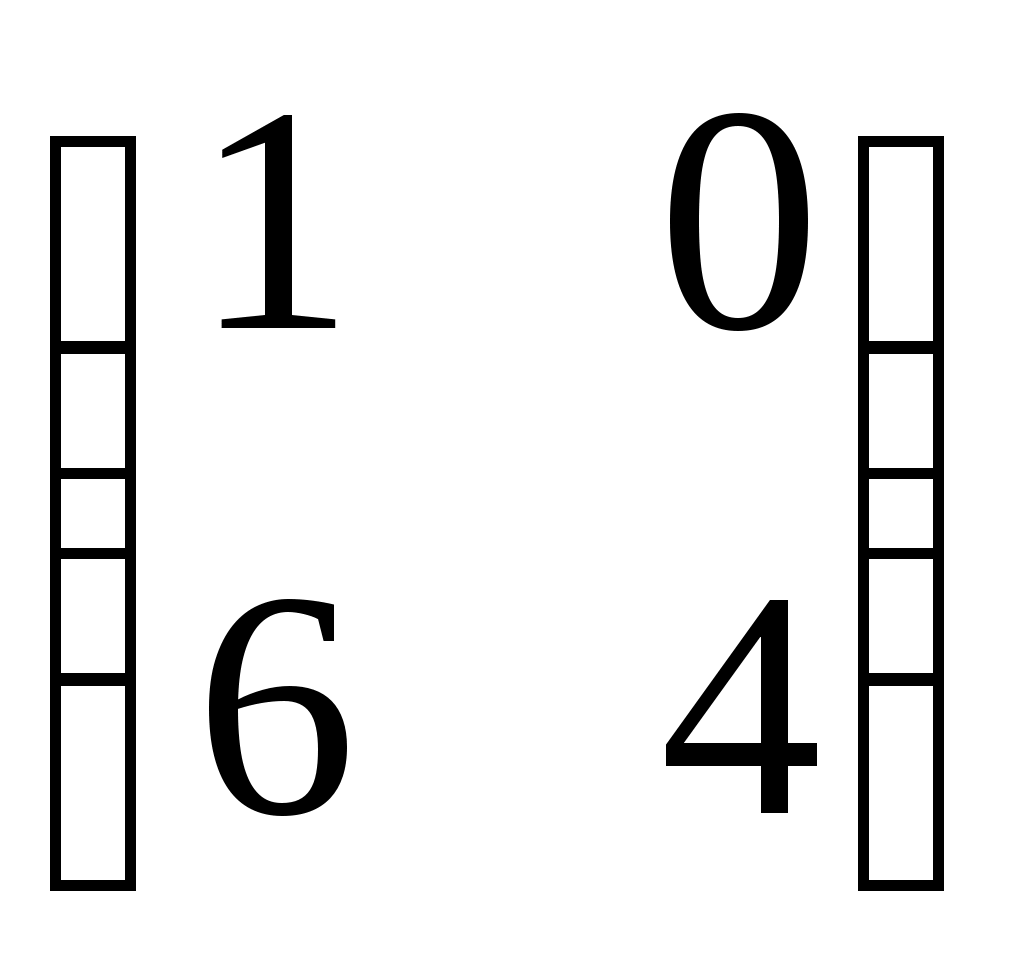 3. 3.  4. 4. 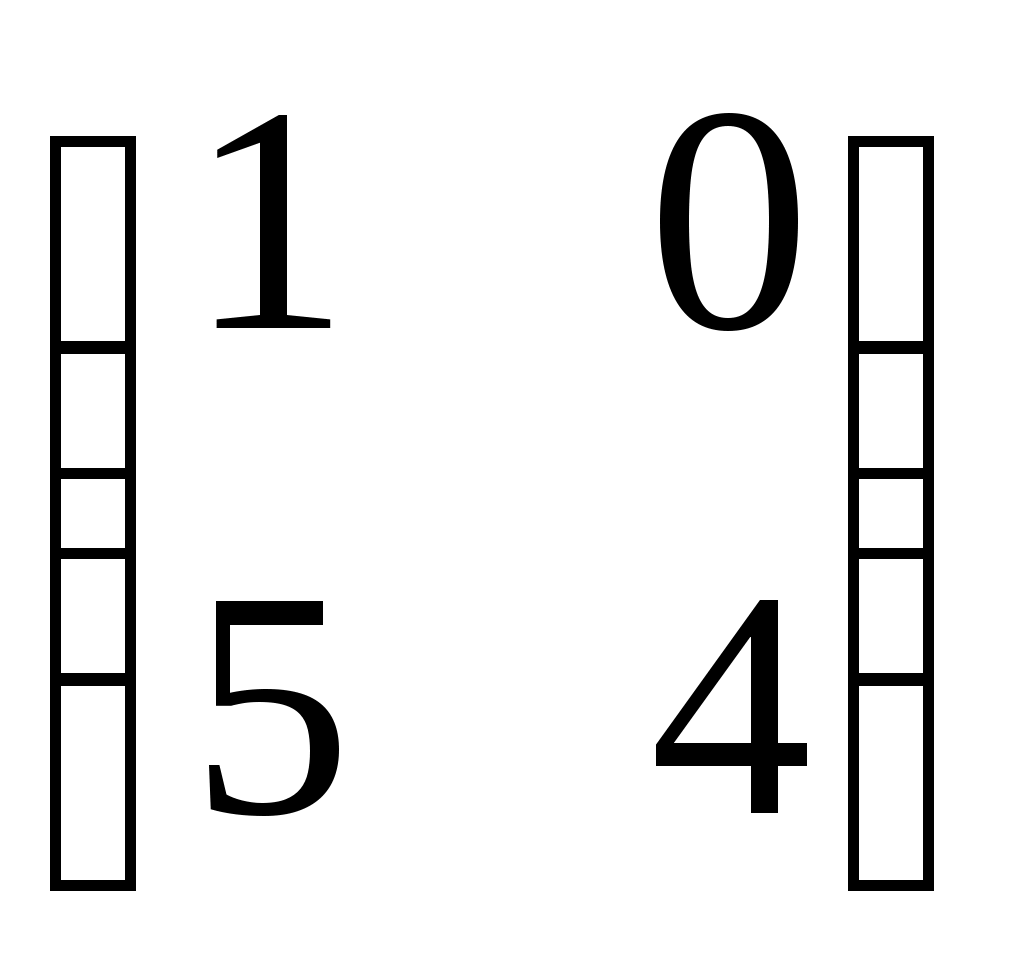
|
 Скачать 0.59 Mb.
Скачать 0.59 Mb.