Бармалей. 1 категория
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
| | ТеоремаКронекера-Капелли: Система m линейных уравнений с n неизвестными имеет бесконечное множество решений, если … ( | |
| | Какой определитель отличен от 0? | 1. 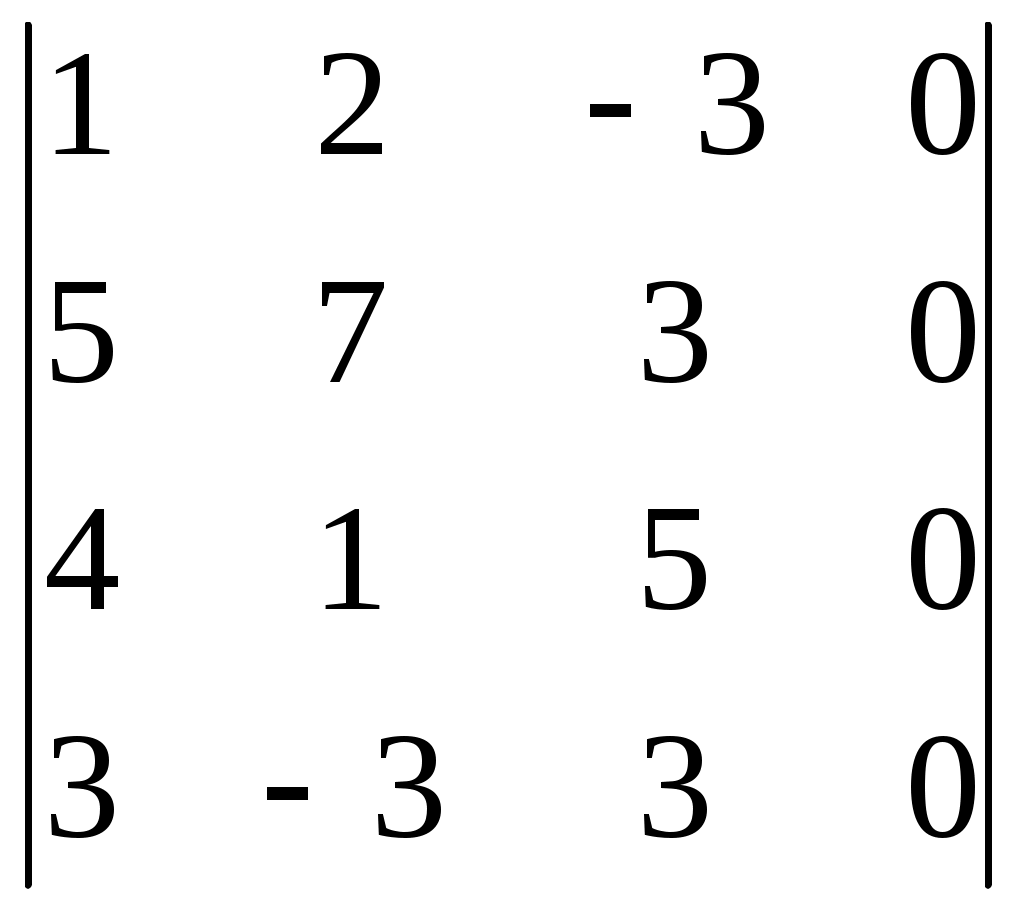 2. 2. 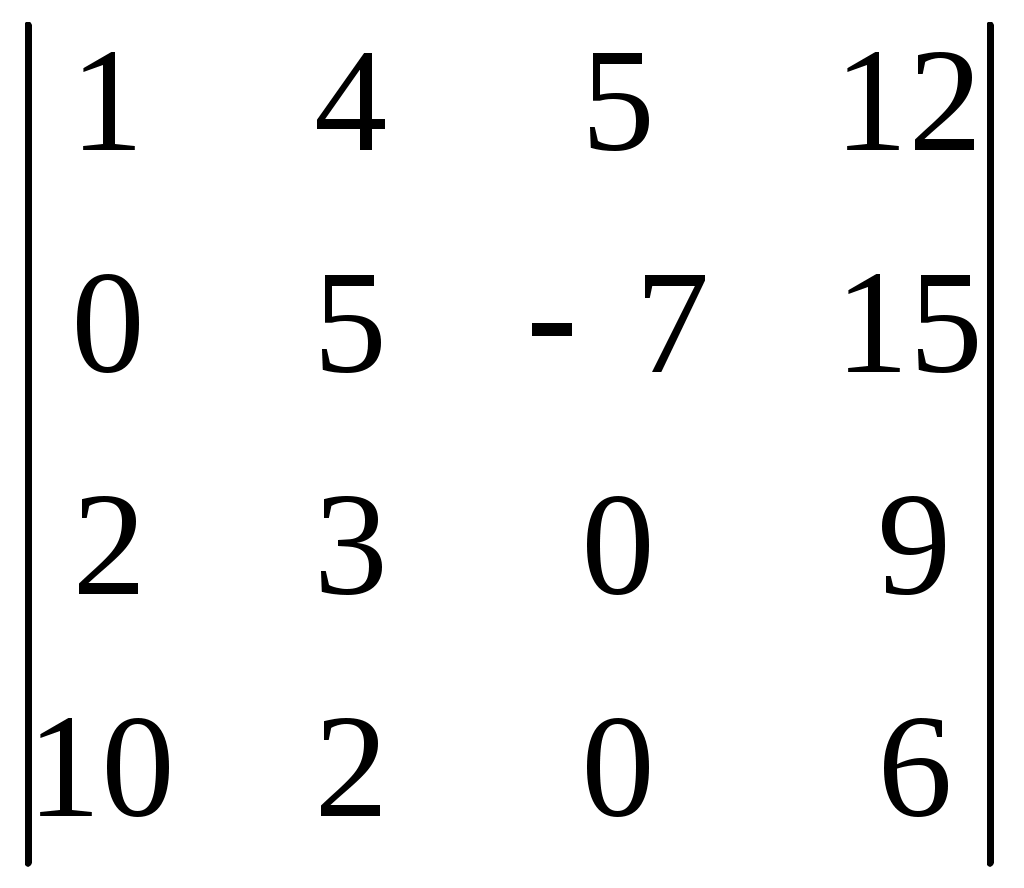 3. 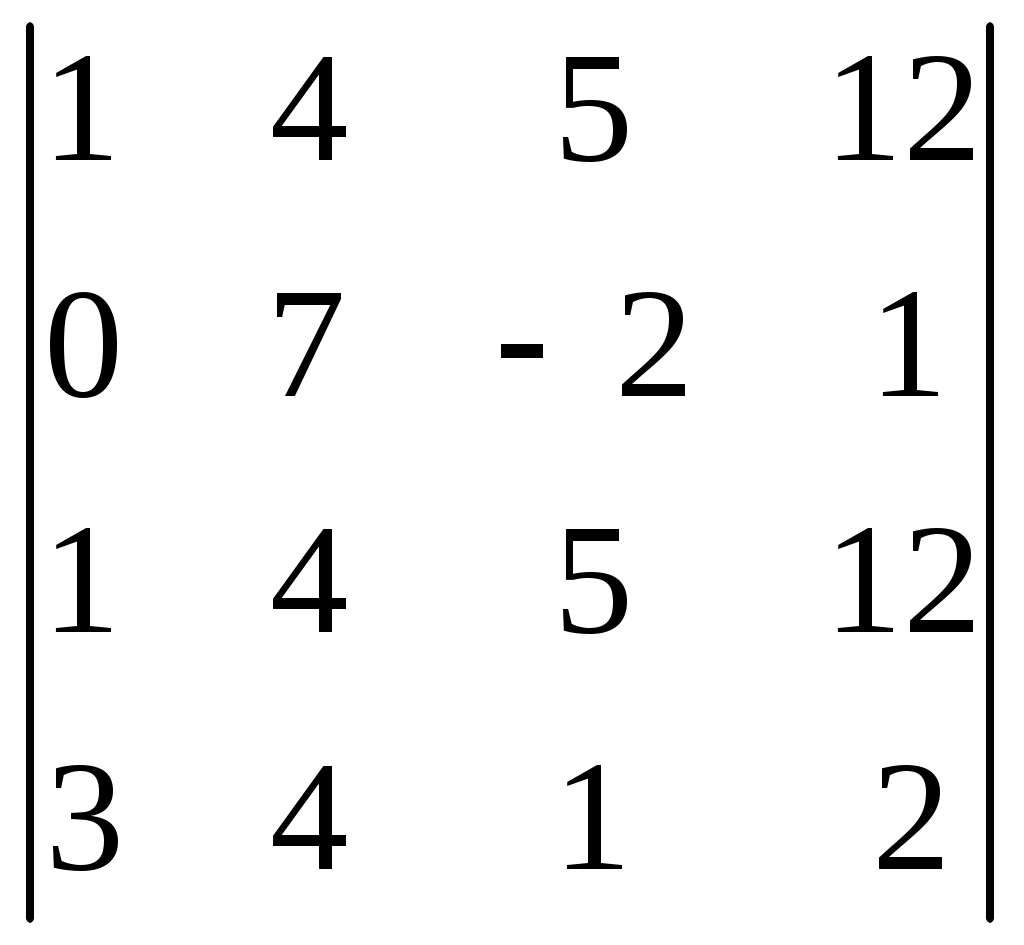 4. 4.  |
| | C помощью правила треугольников можно вычислить | 1.определитель второго порядка 2. определитель любого порядка 3. определитель третьего порядка 4.правило не предназначено для вычисления определителей |
| | Сколько решений имеет система mуравнений с n неизвестными, если ранг матрицы коэффициентов (Здесь | Одно Бесконечное множество Система не имеет решений |
| | Для того, чтобы система n линейных однородных алгебраических уравнений с n неизвестными имела решения, отличные от нулевого, необходимо и достаточно, чтобы | Определитель, составленный из её коэффициентов, был отличен от 0 Определитель, составленный из её коэффициентов, был равен 1 Определитель, составленный из её коэффициентов, был равен n Определитель, составленный из её коэффициентов, был равен 0 |
| | Сумма парных произведений элементов какой-либо строки (столбца) определителя на их алгебраические дополнения равна: | 1. 0 2. 1 3. 2 4. значению определителя |
| | Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы | A была квадратной А была квадратной и det A был отличен от 0 det A был отличен от 1 det A был равен 0 |
| | В результате умножения матрицы 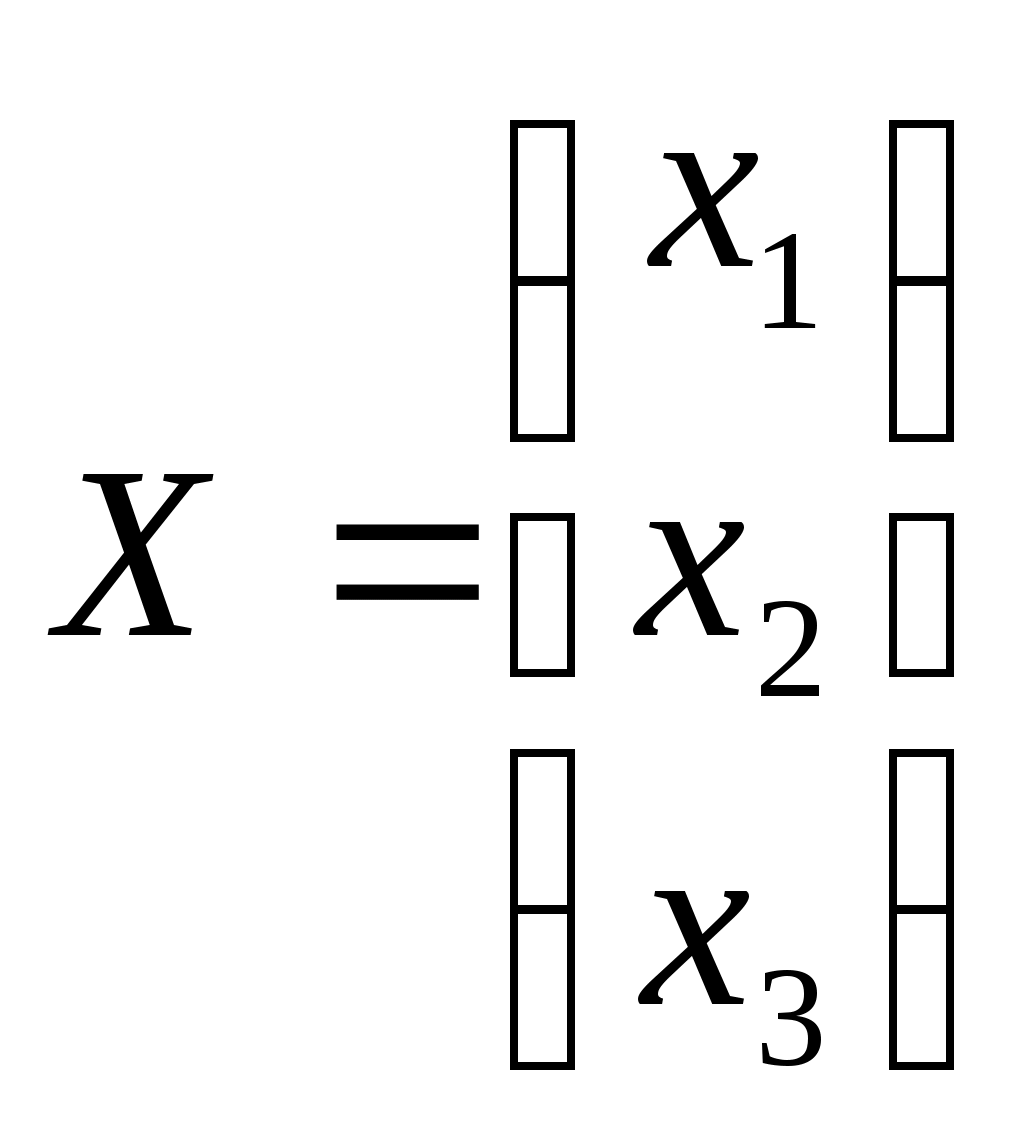 на матрицу на матрицу | 1. 1X1 2. 3X1 3. 1X3 4. 3X3 |
| | Сколько решений имеет система, если ее расширенная матрица после преобразований имеет вид: 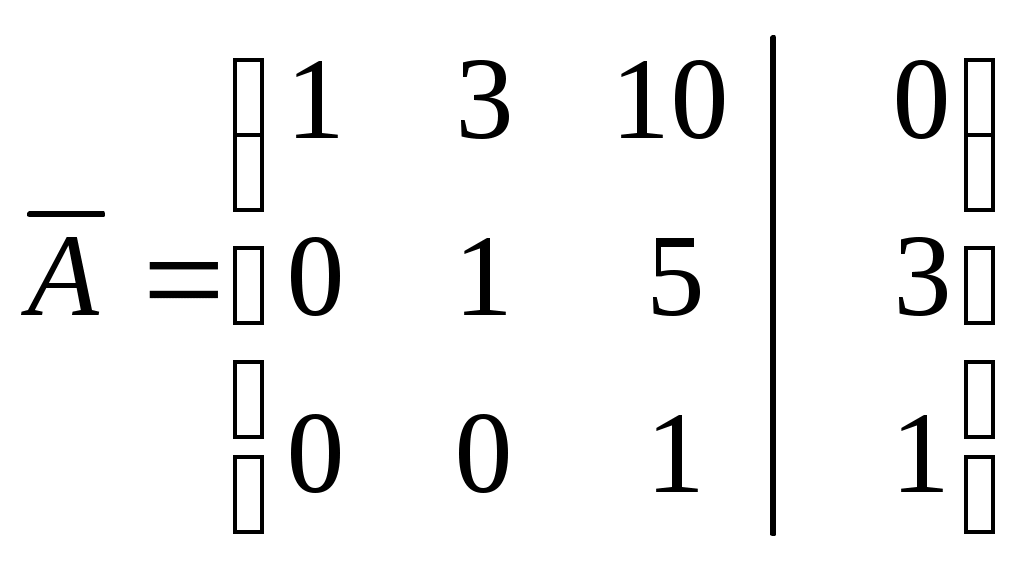 ? ? | Два Одно Бесконечное множество Система не имеет решений |
| | Пусть A – произвольная матрица. Тогда | 1. |
| | Найти элемент 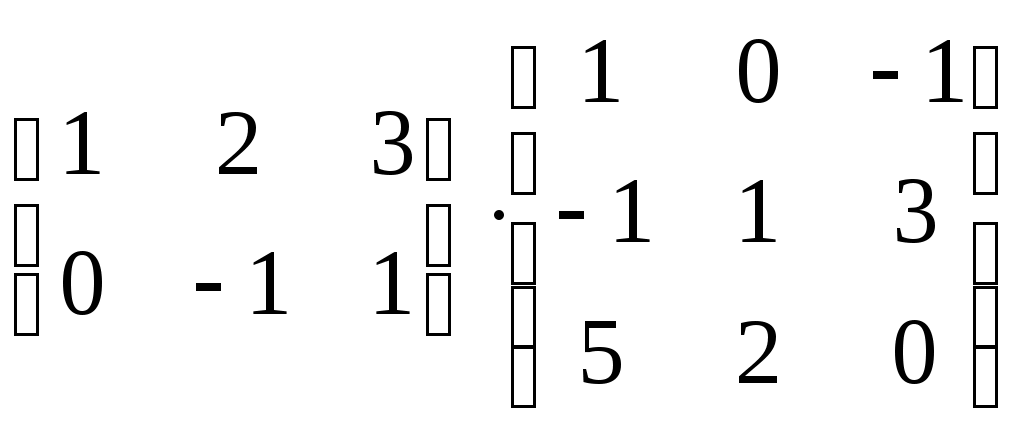 | 1. 1 2. |
| | Теорема Крамера: если определитель системы из n линейных уравнений с n неизвестными | Система не имеет решений Система имеет бесконечное множество решений Система имеет единственное решение Система имеет nрешений |
| | Если с помощью элементарных преобразований произвольная матрица приведена к трапецеидальной форме, то ранг этой матрицы равен | числу ненулевых элементов трапецеидальной матрицы числу всех элементов трапецеидальной матрицы сумме всех ненулевых элементов трапецеидальной матрицы числу ненулевых строк трапецеидальной матрицы |
| |
